Adaptive Blending Method of Radar-Based and Numerical Weather Prediction QPFs for Urban Flood Forecasting

Abstract

Preparing proper disaster prevention measures is important for decreasing the casualties and property losses resulting from floods. One of the most efficient measures in this regard is real-time flood forecasting using quantitative precipitation forecasts (QPFs) based on either short-term radar-based extrapolation or longer-term numerical weather prediction. As both methods have individual advantages and limitations, in this study we developed a new real-time blending technique to improve the accuracy of rainfall forecasts for hydrological applications. We tested the hydrological applicability of six QPFs used for urban flood forecasting in Seoul, South Korea: the McGill Algorithm for Prediction Nowcasting by Lagrangian Extrapolation (MAPLE), KOrea NOwcasting System (KONOS), Spatial-scale Decomposition method (SCDM), Unified Model Local Data Assimilation and Prediction System (UM LDAPS), and Advanced Storm-scale Analysis and Prediction System (ASAPS), as well as our proposed blended approach based on the assumption that the error of the previously predicted rainfall is similar to that of current predicted rainfall. We used the harmony search algorithm to optimize real-time weights that would minimize the root mean square error between predicted and observed rainfall for a 1 h lead time at 10 min intervals. We tested these models using the Storm Water Management Model (SWMM) and Grid-based Inundation Analysis Model (GIAM) to estimate urban flood discharge and inundation using rainfall from the QPFs as input. Although the blended QPF did not always have the highest correlation coefficient, its accuracy varied less than that of the other QPFs. In addition, its simulated water depth in pipe and spatial extent were most similar to observed inundated areas, demonstrating the value of this new approach for short-term flood forecasting.

1. Introduction

Recent climate changes and abnormal weather phenomena have resulted in increased occurrences of localized torrential rainfall in urban areas, such the notable flood disasters in Seoul, South Korea in 2010 and 2011. Aspects of urban hydrological environments (such as reduced concentration time, decreased storage rate, and increased peak discharge) have changed in relation to precipitation, altering and accelerating the severity of flood damage in such areas. Thus, effective disaster prevention measures are increasingly important for decreasing flood-related casualties and property losses. One of the most efficient measures is real-time flood forecasting using quantitative precipitation forecasts (QPFs). Because real-time flood prediction requires sufficient lead time for effective responses, it is common to use rainfall forecasts produced from radar or numerical weather prediction models. However, because these are constrained by uncertainties in the forecasting process (such as differing algorithms or input data), the actual and predicted flood processes differ in time, volume, and spatial extent.

Radar-based nowcasting issues short-term forecasts (1–6 h) using extrapolation, translation, and storm-cell tracking methods without dynamic atmospheric analysis; its accuracy, therefore, decreases as the lead time increases because it cannot resolve the growth and decay of storms. In contrast, numerical weather prediction (NWP) depends on synoptic observations and dynamic atmospheric analysis to produce more reliable forecasts of convection growth and decay with longer lead times. However, the problem of model spin-up time is a significant limitation to the application of NWP models to the nowcasting of precipitation [1,2].

In order to provide more accurate predictions with longer lead times, blending techniques combining NWP models with radar-based forecasts are widely utilized. The first blended forecasts were the Nowcasting and Initialization of Modelling Using Regional Observation Data System (NIMROD) and the Generating Advanced Nowcasts for Deployment in Operational Land Surface Flood Forecasting (GANDOLF) systems [3,4]. More recent nowcasting systems using this approach include Rainstorm Analysis and Prediction Integrated Data-processing System (RAPIDS) and Short-Term Ensemble Prediction System (STEPS) [5,6].

The most important issue when applying the blending method is how to weight spatial and temporal factors. Optimal predictions can be obtained by assigning weights obtained from extrapolation forecasts for the first few hours and from NWP models afterward [3,5,7]. Lin et al. [8] attempted to optimize a blending scheme statistically by exploring the best lead time with changing products in an operational configuration. This approach was further addressed by Ebert and Seed [9], who outlined the limitations of blended methods. In order to compensate for these limitations, a recent trend toward offering probabilistic forecasts (including uncertainty of precipitation rather than simple deterministic forecasts of location and quantity) has been explored.

Most previous studies dealing with blending radar-based extrapolation and NWP models used a sum of weights calculated from both fields. Such weighting functions are determined by the predictive ability of these methods as derived from suitable quality metrics including deterministic [3,10] or probabilistic [6] measurements based on radar reflectivity [11], rainfall rate [3], or probability of precipitation [12]. The performance of such methods has been examined by applying linear [7] or exponential [13] weights to the models. Additionally, a scale-dependent stochastic approach to calculating probabilistic precipitation forecasts was applied by Bowler et al. [6].

Blending techniques can also be divided into deterministic and adaptive techniques depending on how weights are updated for merging [14]. The former blends a local forecast (at a point based on observed persistence or a trend at that location) and an NWP model forecast in a weighted average, where the weights of the two components vary with time t according to a deterministic formula. However, this method is unnecessarily limited in use, and there has been a recent trend away from simple deterministic forecasts of precipitation location and quantity toward offering probabilistic forecasts that include a measure of uncertainty. As the relative reliability of local and model forecasts vary, a method that accounts for the recently observed performance of both can be used to adapt the weights used for blending. The adaptive method used for this purpose can itself have significant time-dependent errors. Whether such risks outweigh the benefits of adaptation is something that must be decided individually (i.e., by variable, location, or season, etc.).

A number of adaptive blending schemes are more sophisticated than the deterministic blending described above, all of which are based on forecasting the change from present conditions and adding that change to the current observed value. In order to complement the limitations of blending techniques using weights derived from statistical analyses, in this study we developed a real-time adaptive blending technique that better reflects the variability of storms. We then analyzed the hydrological applicability of each QPF approach to urban flood forecasting.

2. Materials and Methods

2.1. Data and Study Area

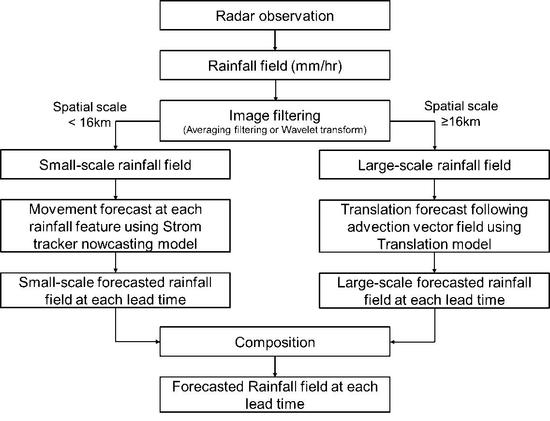
2.1.1. Radar-Based QPFs

We used three kinds of radar-based QPF data in this study, all of which were generated with 1 km spatial resolution and 10 min temporal resolution. The longest prediction lead-time was 6 h.

The first QPF was generated by the Spatial-scale Decomposition method (SCDM) used to forecast differential motions (such as for convective or stratiform cells) in the same precipitation system, following the procedures shown in Figure 1. The rainfall field was separated using image filtering, the movement of small-scale rainfall fields (<16 km) was forecasted by a nowcasting model, and the advection vector of large-scale rainfall fields was estimated by a translation model, then each forecasted field was composited. The smaller-scale convective cells (~2–20 km) had shorter life spans and less predictability than the larger storm envelopes (~20–200 km). The shorter predictability of the small-scale features is directly related to their differential advection velocities and the growth and decay process occurring inside the storm [15].

The other two radar-based short-term forecasts we used, the McGill Algorithm for Prediction Nowcasting by Lagrangian Extrapolation (MAPLE) and KOrea NOwcasting System (KONOS), were produced by the Korea Meteorological Administration (KMA). MAPLE uses radar composite maps to predict the location of precipitation echoes up to 6 h in advance using the variational echo tracking method and a semi-Lagrangian backward advection technique. The algorithm was originally developed by Laroche and Zawadzki [16] to retrieve three-dimensional wind fields from clear-air echoes observed from a single-Doppler radar. Germann and Zawadzki [17] adapted it to determine the velocity field of continental-scale radar composites. This system has been operated in real-time by KMA weather forecasters since June 2008. MAPLE uses a radar rainfall composite with a 1024 × 1024 km domain and a spatial resolution of 1 km centered on the Korean Peninsula and performs 6 h predictions every 10 min. However, it does not incorporate a dynamic precipitation process, which is a fundamental limitation that causes lower prediction scores beyond three hours from initiation. Germann et al. [18] discussed sources of uncertainty in MAPLE predictions associated with the growth or dissipation of precipitation echoes as well as with changes in the echo motion field over the forecast period.

KONOS is a new system that was developed to combine the advantages of MAPLE and very-short-range forecasting (VSRF) to improve the predictability of very short-range forecasts. The initial field used for the extrapolation of KONOS was a Radar-AWS Rainrate system (RAR) used to calibrate the rain intensities (AWS stands for automatic weather stations). The echo-moving vectors for extrapolation were then calculated by the variational echo tracking (VET) algorithm in MAPLE. The semi-Lagrangian method in MAPLE was applied to extrapolate the initial rain intensities [19].

2.1.2. Numerical Weather Prediction Models

We used NWP products estimated by the KMA using the Unified Model Local Data Assimilation and Prediction (UM LDAPS) along with the Advanced Storm-scale Analysis and Prediction System (ASAPS). KMA releases weather forecast data based on the UM 1.5 km L70, an operational short-range local NWP suite introduced in 2012 that runs four times daily (00/06/12/18 UTC) to produce 36 h forecasts with three hourly 3DVAR cycles, and Korea Local Analysis and Prediction System (KLAPS) (5 km L40), a local VSRF system that analyzes weather conditions around the Korean Peninsula every hour. Regarding the UM LDAPS data, we could not change the original settings of the KMA numerical weather prediction model. Although the original UM LDAPS data have a 1.5 km resolution, we interpolated these data to a 1 km resolution to maintain a homogeneous spatial resolution with the other QPFs and for convenience when applying the blending method [20].

KMA also employs the National Oceanic and Atmospheric Administration (NOAA)’s Local Analysis and Prediction System (LAPS), which provides the hot-start initial condition to the ASAPS based on the Weather Research and Forecasting (WRF) model [21]. LAPS is a meteorological data assimilation tool that employs a suite of observations to generate a realistic, spatially distributed, time-evolving, and three-dimensional representation of atmospheric features; this also provides the initial condition to the forecasting system. ASAPS was developed for monitoring severe weather and consists of a 265 × 265 km grid with a spatial resolution of 1 km centered on the Seoul metropolitan area and performs six-hour forecasts with one-hour intervals.

2.1.3. Study Area

Seoul is one of the most highly urbanized cities in South Korea with several residential areas and industrial facilities located near flood plains that are at risk from damage caused by urban flooding. Several researchers, and even the South Korean government, have worked to develop flood forecasting systems and methodologies for urban flood disaster mitigation [22,23,24]. Moreover, many kinds of QPF data are issued for the Seoul metropolitan area by the KMA, allowing us to easily evaluate the hydrological applicability and accuracy of various QPFs. We chose two specific drainage basins within Seoul (Gangnam and Bakwoon) as shown in Figure 2. Gangnam is representative of Seoul’s downtown area where residential and commercial areas are concentrated; this is a low-lying location with a more complicated sewer network than surrounding areas, making this area vulnerable to flooding during heavy rainfall. Bakwoon basin, in the northern part of Seoul near the Jung-rang River, is a residential area that also suffers from river flooding and inundation.

2.2. Methodology

2.2.1. Adaptive Blending Using the Harmony Search Algorithm

We developed an adaptive blending method to find the optimal weight for real-time blending of the three QPFs at each forecast time using the harmony search (HS) method. This is a metaheuristic music-inspired algorithm used to solve a wide range of optimization problems in different fields [25,26,27,28]. When musicians compose a harmony, they test various possible combinations of the pitches stored in their memory, which can be considered as an optimization process that adjusts the input (pitches) to obtain the optimal output (perfect harmony). This approach has two essential parameters: the harmony memory considering rate (HMCR) and the pitch adjusting rate (PAR).

The HS process follows four steps (Figure 3). First, the harmony memory (HM) is initialized, consisting of a given number of randomly generated solutions to the optimization problems. Second, a new solution vector is improved from the HM, with each component of the solution obtained based on the HMCR through memory considerations, pitch adjustments, and a randomization process. Third, the HM is updated and the new solution from step two is evaluated. If it yields a better fitness than that of the worst member in the HM, it will replace that one; otherwise it is eliminated. Fourth, steps two and three are repeated until a preset termination criterion (e.g., the maximal number of iterations) is met.

The proposed blending technique is based on the assumption that the error of previously predicted rainfall is similar to current predicted rainfall. Weights are calculated every 10 min using ground observation rainfall data that correspond to past forecast precipitation. Using Equation (1), the sum of each weight shall be 1 + α, where α is intended to compensate for the quantitative errors of past ground observation and forecasted rainfall. The combined weights of Equation (1) are then determined to minimize the root mean square error (RMSE) between previous predicted rainfall and observed gauge rainfall for the previous one-hour lead time every 10 min, as in Equations (2) and (3). The blended QPF is estimated by Equation (4).

$$C_{MAPLE}+C_{KONOS}+C_{SCDM}+C_{UM}+C_{ASAPS}=1+\alpha ,$$

(1)

$$Fitness=\min \left[RMSE\right],$$

(2)

$$\mathrm{RMSE}=\sqrt{\frac{1}{N}{{\displaystyle \sum }}_{t=1}^N{\left(R_{gauge}^t-R_{BLENDED}^t\right)}^2},\mathrm{and}$$

(3)

$$\begin{gathered} R_{BLENDED}=C_{MAPLE}\times R_{MAPLE}+C_{KONOS}\times R_{KONOS}+C_{SCDM}\times R_{SCDM}+C_{UM }\times R_{UM}+ \\ {C}_{ASAPS}\times R_{ASAPS}, \end{gathered}$$

(4)

where C_MAPLE, C_KONOS, C_SCDM, C_UM, and C_ASAPS are weights determined by the harmony search process, $R_{gauge}^t$ is the ground-observation rainfall, and $R_{BLENDED}^t$ is the blended QPF using the weights of all QPFs for the past 1 h and 10 min intervals; therefore, N is 6.

2.2.2. Hydrologic and Hydraulic Models for Urban Flood Forecasting Using Various QPFs

We used the Storm Water Management Model (SWMM) and a 2-dimensional inundation analysis model to evaluate the performance of the various QPF products. The SWMM, which was developed with the support of the U.S. Environmental Protection Agency, is commonly applied to runoff analysis in urban areas [23,24,29]. It simulates flow movements during real storm events based on rainfall and drainage system characteristics to estimate quantitative discharge and water quality information. The model simulates runoff and quality constituents from rainfall with simple routing and kinetic wave approximations using the full Saint-Venant equation; it can simulate dynamic backwater conditions, looped drainage networks, surcharging, and pressure flow [29,30]. We set up the Grid-based Inundation Analysis Model (GIAM) based on the 2-dimensional shallow water equation of continuity and momentum to simulate urban surface inundation by routing overland flow with sources coming from the surcharge flow at manholes [31].

3. Results

3.1. Real-Time Blending and Analysis of QPF Accuracy

We selected three rain events to determine the blended forecasting rainfall by applying real-time blending techniques and to assess the accuracy of real-time radar-based QPF, NWP QPF, and bound QPF: 1 July 2016, 14:00–15:50 (Case 1), 1 July 2016, 19:00–23:50 (Case 2), and 5 July 2016, 09:10–10:50 (Case 3). The maximum rainfall in these cases occurred at 15:40, 22:10, and 10:10, respectively. These represent typical occurrences of heavy rainfall in summer in Seoul, especially with regard to the flood damage caused by heavy rainfall that actually occurred in Case 3.

Figure 4 compares quantitative precipitation estimates (QPE, from the KMA Rainrate system) with MAPLE, KONOS, and SCDM rainfall data generated with 1–3 h lead times starting at 09:20 in Case 3. After a 1 h lead time, all three QPFs differed in rainfall intensity from the corresponding QPE, but their spatial distribution was similar. However, after a 2 h lead time, all three QPFs clearly differed from the QPE in spatial distribution as well. Similarly, Figure 5 compares QPE data with NWP rainfall data generated with 1–3 h lead times starting at 09:00 in Case 3. The NWP data also show different rainfall distributions and intensities for each lead time, which seems to be due to differences in the prediction methods.

Since the variability of predicted rainfall is rather large, due to different data sources and forecasting techniques, the accuracy of hydrologic forecasting is strongly influenced by which rainfall prediction is used. Therefore, we used various QPFs and blended QPF to evaluate hydrological applicability in this study.

We evaluated the quantitative accuracy of three radar-based QPFs (SCDM, MAPLE, KONOS), and the two NWP QPFs (UM LDAPS, ASAPS), along with the blended QPF, using observed rainfall data from 25 stations in Seoul as the true rainfall. The evaluation was performed every 10 min for lead times from 10–360 min, using RMSE and correlation coefficient (r) as the verification criteria.

The correlation coefficient differed depending on the predicted rainfall type and the QPF update time (Figure 6). The correlation coefficient of the blended QPF was better than those of the other QPFs at the time of maximum rainfall in Case 1, but in Cases 2 and 3 this was higher than that of NWP QPF but lower than that of the radar-based QPFs. Although the blended QPF did not always have the highest correlation coefficient, its accuracy variation was not as large as those of the other QPFs due to the merging effect.

The RMSE for all QPFs became smaller over time (Figure 7). As the analysis periods ran from the beginning to the end of precipitation, the RMSE naturally declined due to the smaller amount of rainfall at termination. Therefore, we analyzed errors between the QPFs relative to the computation time rather than as the absolute RMSE at each computation time. The RMSE of the ASAPS QPF had larger fluctuations in Cases 1 and 2 at each computation time, while the variations in RMSE for the three radar-based QPFs were similar and not larger than those of the NWP QPFs. The RMSE of the blended QPF tended to match that of the radar based QPFs; in Cases 1 and 2, the RMSE of the blended QPF was lowest at the time of maximum rainfall occurrence. Figure 8 shows the time series of the weights of all models estimated from the HS method for Case 3; the blended QPF is estimated using these weights.

3.2. Analysis of Real-Time Urban Runoff Forecasting Using QPFs

We used the SWMM to perform real-time urban runoff forecasting using the radar-based, NWP-based, and blended QPFs to assess the hydrological applicability of using QPF. The two study areas, in the Gangnam and Bakwoon basins, are locations where inundation and overflow often occur (Figure 9). The SWMM input of the Gangnam drainage system comprises 1059 pipes, 773 manholes, and 772 sub-basins over a 7.4 km² area. Water depth in pipe was recorded at three observation stations for evaluation. The Bakwoon basin test is discussed in Section 3.3.

The three previously defined cases were used for evaluation of urban runoff forecasting with the rainfall input for the SWMM model produced by QPE and QPF at each current time (CT) for 3 h ahead of forecast. Figure 10 compares the observed and simulated depths using all QPFs for Case 1 from 14:00–15:50. The ASAPS QPF effectively simulated the peak water depth occurrence time and water depth change patterns. In addition, the blended QPF showed the second-best simulation results at 15:30 and 15:50. The radar-based and UM LDAS QPFs could not accurately simulate the peak flow and showed significantly lower simulated sewer water depths. Statistical evaluations showed that the relative error of peak depth (REPD) for ASAPS was the lowest (−19.11% to 11.66%) of all QPFs while RMSE for the blended model was lowest (0.33–0.38) (

Table 1. Evaluation results for simulated water depth using various QPF products (Case 1) in terms of correlation coefficient (r), relative error of peak depth (REPD), and root mean square error (RMSE) by current time (CT).

CT	AWS			MAPLE			KONOS			SCDM			UM			ASAPS			BLENDED
	r	RMSE	REPD	r	RMSE	REPD	r	RMSE	REPD	r	RMSE	REPD	r	RMSE	REPD	r	RMSE	REPD	r	RMSE	REPD
15:00	0.63	0.32	−0.71	−0.30	0.49	−84.67	−0.20	0.49	−83.37	0.59	0.37	−42.60	−0.56	−0.55	−76.51	0.32	0.49	0.65	0.51	0.36	−62.89
15:30	0.57	0.34	1.42	0.40	0.48	−64.70	0.44	0.47	−60.77	0.42	0.44	−54.20	−0.58	−0.58	−76.15	0.14	0.51	−19.11	0.40	0.38	−34.79
15:50	0.80	0.22	2.78	0.42	0.41	−8.52	0.52	0.36	14.55	0.55	0.35	−0.89	0.37	−0.36	−0.83	0.21	0.47	11.66	0.48	0.33	−2.07

).

Figure 11 compares results for Case 2 at 21:00, 21:30, and 22:00. The blended QPF accurately simulated the peak water depth occurrence time and water depth change patterns. When rainfall decreased, the NWP-based QPF was overestimated and affected the overestimate of the blended predicted rainfall. On the other hand, the radar-based QPFs were underestimated at all current times. Statistically, the blended QPF had the lowest REPD and RMSE in Case 2, ranging from −14.0 to −27.08 and 0.31–0.60, respectively (

Table 2. Evaluation results for simulated water depth using various QPF products (Case 2) in terms of correlation coefficient (r), relative error of peak depth (REPD), and root mean square error (RMSE) by current time (CT).

CT	AWS			MAPLE			KONOS			SCDM			UM			ASAPS			BLENDED
	r	RMSE	REPD	r	RMSE	REPD	r	RMSE	REPD	r	RMSE	REPD	r	RMSE	REPD	r	RMSE	REPD	r	RMSE	REPD
21:00	0.76	0.34	−6.67	0.40	0.67	−65.03	0.30	0.61	−65.03	0.47	0.65	−65.02	−0.57	0.79	−12.51	0.68	0.79	35.08	0.01	0.50	−27.08
21:30	0.82	0.32	2.41	0.49	0.56	−55.54	0.60	0.48	−53.44	0.62	0.51	−54.00	−0.61	0.90	−10.05	0.80	0.73	38.05	0.83	0.31	−15.79
22:00	0.87	0.28	−7.64	0.98	0.35	−45.44	0.87	0.32	−43.79	0.98	0.37	−47.18	−0.06	0.88	−10.56	−0.12	1.02	15.38	0.51	0.60	−14.00

).

Figure 12 compares results for Case 3 at 09:20, 09:30, and 09:40. The blended QPF and ASAPS had higher accuracy than those the other QPFs in terms of peak water depth occurrence time and peak water depth. In particular, since the merged QPF is affected by the radar QPF (updated every 10 min), it follows the temporal variation of the rainfall more than the ASAPS, which updates every hour. All evaluation indicators showed good results for blended QPF (

Table 3. Evaluation results for simulated water depth using various QPF products (Case 3) in terms of correlation coefficient (r), relative error of peak depth (REPD), and root mean square error (RMSE) by current time (CT).

CT	AWS			MAPLE			KONOS			SCDM			UM			ASAPS			BLENDED
	r	RMSE	REPD	r	RMSE	REPD	r	RMSE	REPD	r	RMSE	REPD	r	RMSE	REPD	r	RMSE	REPD	r	RMSE	REPD
9:20	0.94	0.22	−2.00	0.81	0.53	−59.39	0.89	0.55	−63.22	0.83	0.48	−61.67	0.89	0.58	−67.11	0.89	0.33	−24.50	0.92	0.26	−15.83
9:30	0.93	0.24	5.78	0.85	0.48	−50.50	0.83	0.46	−34.89	0.90	0.51	−51.50	0.93	0.51	−52.66	0.91	0.30	−28.39	0.94	0.24	−19.11
9:40	0.92	0.25	0.44	0.92	0.47	−53.78	0.83	0.43	−30.11	0.92	0.54	−55.11	0.93	0.46	−51.39	0.93	0.27	−25.56	0.95	0.20	−8.67

).

3.3. Analysis of Real-time Urban Inundation Forecasting Using QPFs

We analyzed the effects of all tested QPFs by forecasting inundation in an urban area using existing information for 5 July 2016, an event that caused actual flood damage in the Bakwoon area. Inundated areas included the Surak underpass structure and the Sanggye-dong multiplex houses (Figure 13). The inundation information consisted of digital photos taken at the inundation sites. The SWMM model was set up as shown in Figure 9b with input data from 1163 manholes, 1125 pipes, and 1081 sub-basins over a 9.1 km² area. The GIAM was then set up with a spatial resolution of 6 m and a time interval of 0.05 s.

Figure 14 shows the surcharge flow from the manhole where the maximum amount of overflow occurred (red star of Figure 12) as simulated by all QPFs and AWSs. As there was no water depth observation station in the Bakwoon basin, we compared simulated surcharge flow using AWS data. The blended model is most similar to the rain gauge data in terms of peak surcharge flow and timing.

Figure 15 shows the maximum inundation maps for AWS data and each QPF, which are noticeably different. Because no observed inundation map exists, only photos, the accuracy comparison for the inundation forecasting is based on simulation results from the AWS-observed rainfall. MAPLE is significantly underestimated inundation while the ASAPS and UM LDAPS results were similar to AWS result. The radar-based and NWP QPFs all predicted flooding only at the Surak underpass structure. The blended QPF simulation was most similar to the observed spatial extent of flood inundation and was the only model to predict flooding at the Sanggye-dong multiplex houses.

The forecasting results showed a maximum inundation depth for the blended QPF of 6.36 m, close to the AWS result (6.70 m) (

Table 4. Inundation forecast results in terms of max depth and inundated area for each criterion.

Criteria	AWS	MAPLE	KONOS	SCDM	UM	ASAPS	BLENDED
Max Depth (m)	6.70	4.49	5.81	6.45	6.10	6.05	6.36
Inundated area over 20 cm (m2)	11,376	144	2376	7596	5148	4068	9180
Inundated area over 40 cm (m2)	11,268	72	1512	5328	3600	3888	6588
Inundated area over 60 cm (m2)	9036	36	360	3600	4248	3240	3600

). For the AWS result, the inundated area exceeding 20 cm depth was 11,376 m² and the blended result was a similar 9180 m². The inundated areas of the other QPFs were much smaller than the AWS result. For the inundated area exceeding 40 cm, all QPF results were considerably smaller than the AWS result; the blended QPF’s inundated area was 6588 m², about 40% smaller than the AWS result. These results confirm the usefulness of the blended QPF approach for urban flood forecasting. However, future research should consider the data period used for blending the weight and production time of the forecasting model, considering the influence of past forecast errors when estimated the blending weights and the influence of different forecasting techniques.

4. Conclusions

In this study, we developed a new real-time adaptive blending technique using the harmony search algorithm to improve the accuracy of rainfall forecasts for hydrological applications. Three radar-based QPFs (MAPLE, KONOS, and SCDM) and two NWP QPFs (UM LDAPS and ASAPS) were used for the blending process. We also assessed the hydrological applicability of the individual and blended QPFs for use in urban flood forecasting in Seoul, South Korea. Our proposed blended approach was based on the assumption that the error of the previously predicted rainfall was similar to that of current predicted rainfall. Using the harmony search algorithm, we optimized real-time weights that would minimize the root mean square error between predicted and observed rainfall for a 1 h lead time at 10 min intervals.

Our accuracy analysis using the six QPFs with three real-life rainfall cases showed that the blended QPF could be calculated with stable accuracy. The SWMM and GIAM models were then used to estimate urban flood discharge and to forecast the inundated area using rainfall from the QPFs and AWS data. Although the blended QPF did not always have the highest correlation coefficient, its accuracy varied less than that of the other QPFs. In addition, its simulated water depth in pipe and spatial extent were most similar to observed inundated areas, demonstrating the value of this new blending approach for short-term flood forecasting. When comparing the inundated areas from AWS data, the predicted inundated areas showed that the blended forecast could more accurately simulate actual inundated locations than any other QPFs.

Our results were limited by the generalized nature of the study, as it assessed the blending technique using only a few rainfall cases in a specific area. However, the improved accuracy of the blended QPF is quite meaningful with regard to this approach’s hydrological applicability in cases of extreme rainfall. Future research should build on these results by assessing more diverse rainfall cases and study areas. In addition, we intend to further optimize the weights using various storm events and criteria while working to improve the prediction accuracy using a spatial blending technique.