Role of Emissivity in Lava Flow ‘Distance-to-Run’ Estimates from Satellite-Based Volcano Monitoring
Abstract
:1. Introduction
2. Materials and Methods
2.1. Rock Samples
2.2. Laboratory-Based Data Acquisition
2.2.1. Emissivity from Surface Reflectance Spectra
2.2.2. Emissivity from Surface Radiance Spectra
2.3. Emissivity from High-Spatial Resolution Satellite Data
The Global Emissivity Database
3. Emissivity Results
3.1. Emissivity from Reflectance
3.2. Emissivity from Radiance
3.3. Comparison with Emissivity from Satellite Data
4. Emissivity versus Effusion Rate and ‘Distance-to-Run’
4.1. From Spaceborne Data
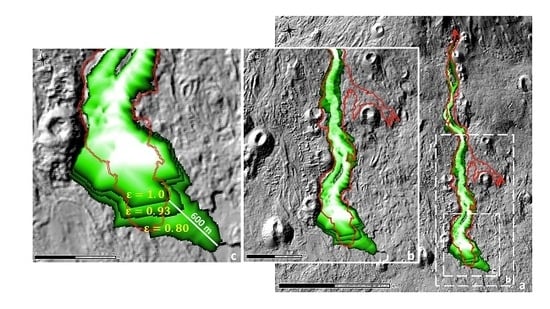
4.2. From Straightforward Modelling
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Garel, F.; Kaminski, E.; Tait, S.; Limare, A. An experimental study of the surface thermal signature of hot subaerial isoviscous gravity currents: Implications for thermal monitoring of lava flows and domes. J. Geophys. Res. Solid Earth 2012, 117, B02205. [Google Scholar] [CrossRef]
- Vicari, A.; Alexis, H.; Del Negro, C.; Coltelli, M.; Marsella, M.; Proietti, C. Modeling of the 2001 lava flow at Etna volcano by a Cellular Automata approach. Environ. Model. Softw. 2007, 22, 1465–1471. [Google Scholar] [CrossRef] [Green Version]
- McGuire, W.J.; Kilburn, C.R.J.; Murray, J.B. Monitoring Active Volcanoes: Strategies, Procedures, Techniques; University of London Press: London, UK, 1995; p. 421. [Google Scholar]
- Harris, A.J.L. Thermal Remote Sensing of Active Volcanoes: A User’s Manual; Cambridge University Press: Cambridge, UK, 2013; p. 736. [Google Scholar]
- Ramsey, M.S.; Fink, J.H. Estimating silicic lava vesicularity with thermal remote sensing: A new technique for volcanic mapping and monitoring. Bull. Volcanol. 1999, 61, 32–39. [Google Scholar] [CrossRef]
- Ball, M.; Pinkerton, H. Factors affecting the accuracy of thermal imaging cameras in volcanology. J. Geophys. Res. Solid Earth 2006, 111, B11203. [Google Scholar] [CrossRef]
- Higgins, J.; Harris, A. VAST: A program to locate and analyse volcanic thermal anomalies automatically from remotely sensed data. Comput. Geosci. 1997, 23, 627–645. [Google Scholar] [CrossRef]
- Wright, R.; Flynn, L.; Garbeil, H.; Harris, A.; Pilger, E. Automated volcanic eruption detection using MODIS. Remote Sens. Environ. 2002, 82, 135–155. [Google Scholar] [CrossRef] [Green Version]
- Wright, R.; Flynn, L.P.; Garbeil, H.; Harris, A.J.; Pilger, E. MODVOLC: Near-real-time thermal monitoring of global volcanism. J. Volcanol. Geotherm. Res. 2004, 135, 29–49. [Google Scholar] [CrossRef]
- Di Bello, G.; Filizzola, C.; Lacava, T.; Marchese, F.; Pergola, N.; Pietrapertosa, C.; Piscitelli, S.; Scaffidi, I.; Tramutoli, V. Robust satellite techniques for volcanicand seismic hazards monitoring. Ann. Geophys. 2004, 47. [Google Scholar] [CrossRef]
- Hirn, B.R.; Di Bartola, C.; Laneve, G.; Cadau, E.; Ferrucci, F. SEVIRI Onboard Meteosat Second Generation, and the Quantitative Monitoring of Effusive Volcanoes in Europe and Africa. In Proceedings of the IGARSS 2008, 2008 IEEE International Geoscience and Remote Sensing Symposium, Boston, MA, USA, 7–11 July 2008; pp. 374–377. [Google Scholar]
- Wooster, M.J.; Rothery, D.A. Time-series analysis of effusive volcanic activity using the ERS along track scanning radiometer: The 1995 eruption of Fernandina volcano, Galápagos Islands. Remote Sens. Environ. 1997, 62, 109–117. [Google Scholar] [CrossRef]
- Coppola, D.; Macedo, O.; Ramos, D.; Finizola, A.; Delle Donne, D.; Del Carpio, J.; White, R.; McCausland, W.; Centeno, R.; Rivera, M.; et al. Magma extrusion during the Ubinas 2013–2014 eruptive crisis based on satellite thermal imaging (MIROVA) and ground-based monitoring. J. Volcanol. Geotherm. Res. 2015, 302, 199–210. [Google Scholar] [CrossRef] [Green Version]
- Harris, A.J.L. Thermal remote sensing of active volcanism: Principles. In Thermal Remote Sensing of Active Volcanoes: A User’s Manual; Cambridge University Press: Cambridge, UK, 2013; pp. 70–112. [Google Scholar]
- Rothery, D.A.; Francis, P.W.; Wood, C.A. Volcano monitoring using short wavelength infrared data from satellites. J. Geophys. Res. 1988, 93, 7993–8008. [Google Scholar] [CrossRef]
- Harris, A.J.; Butterworth, A.L.; Carlton, R.W.; Downey, I.; Miller, P.; Navarro, P.; Rothery, D.A. Low- cost volcano surveillance from space: Case studies from Etna, Krafla, Cerro Negro, Fogo, Lascar and Erebus. Bull. Volcanol. 1997, 59, 49–64. [Google Scholar] [CrossRef]
- Coltelli, M.; Proietti, C.; Branca, S.; Marsella, M.; Andronico, D.; Lodato, L. Analysis of the 2001 lava flow eruption of Mt. Etna from three-dimensional mapping. J. Geophys. Res. Earth Surf. 2007, 112, F02029. [Google Scholar] [CrossRef]
- Tarquini, S.; Isola, I.; Favalli, M.; Mazzarini, F.; Bisson, M.; Pareschi, M.T.; Boschi, E. TINITALY/01: A new triangular irregular network of Italy. Ann. Geophys. 2007, 50, 407–425. [Google Scholar]
- Maturilli, A.; Helbert, J.; D’Amore, M.; Varatharajan, I.; Ortiz, Y.R. The Planetary Spectroscopy Laboratory (PSL): Wide spectral range, wider sample temperature range. In Proceedings of the SPIE 10765: Infrared Remote Sensing and Instrumentation, San Diego, CA, USA, 18 September 2018. [Google Scholar]
- Korb, A.R.; Salisbury, J.W.; Aria, D.M. Thermal-infrared remote sensing and Kirchhoff’s law 2. Field measurements. J. Geophys. Res. Solid Earth 1999, 104, 15339–15350. [Google Scholar] [CrossRef]
- Maturilli, A.; Helbert, J.; Witzke, A.; Moroz, L. Emissivity measurements of analogue materials for the interpretation of data from PFS on Mars Express and MERTIS on Bepi-Colombo. Planet. Space Sci. 2006, 54, 1057–1064. [Google Scholar] [CrossRef]
- NASA; JPL. ASTER Global Emissivity Dataset 100-meter HDF5[37/38/39.012-0-15.0001]; NASA EOSDIS Land Processes DAAC: Sioux Falls, SD, USA, 2014.
- Hulley, G.C.; Hook, S.J.; Abbott, E.; Malakar, N.; Islam, T.; Abrams, M. The ASTER Global Emissivity Dataset (ASTER GED): Mapping Earth’s emissivity at 100 meter spatial scale. Geophys. Res. Lett. 2015, 42, 7966–7976. [Google Scholar] [CrossRef]
- NASA; JPL. LP DAAC: Land Processes Distributed Active Archive Center. 2014. Available online: https://lpdaac.usgs.gov/dataset_discovery/community/community_products_table/ag100_v003 (accessed on 1 June 2018).
- Wyatt, M.B.; Hamilton, V.E.; McSween, H.Y.; Christensen, P.R.; Taylor, L.A. Analysis of terrestrial and Martian volcanic compositions using thermal emission spectroscopy: 1. Determination of mineralogy, chemistry, and classification strategies. J. Geophys. Res. 2001, 106, 14711–14732. [Google Scholar] [CrossRef] [Green Version]
- Hirn, B.; Di Bartola, C.; Ferrucci, F. Spaceborne monitoring 2000-2005 of the Pu’u ‘O’o-Kupaianaha (Hawaii) eruption by synergetic merge of multispectral payloads ASTER and MODIS. IEEE Trans. Geosci. Remote Sens. 2008, 46, 2848–2856. [Google Scholar] [CrossRef]
- Barsi, J.A.; Barker, J.L.; Schott, J.R. An Atmospheric Correction Parameter Calculator for a single thermal band earth-sensing instrument. In Proceedings of the IGARSS 2003, 2003 IEEE International Geoscience and Remote Sensing Symposium, Toulouse, France, 21–25 July 2003; pp. 3014–3016. [Google Scholar]
- Barsi, J.A.; Barker, J.L.; Schott, J.R. Atmospheric Correction Parameter Calculator. 2003 IGARSS03. Available online: https://atmcorr.gsfc.nasa.gov/ (accessed on 1 June 2018).
- Pieri, D.C.; Baloga, S.M. Eruption rate area, and length relationships for some Hawaiian lava flows. J. Volcanol. Geotherm. Res. 1986, 30, 29–45. [Google Scholar] [CrossRef]
- Wright, R.; Blake, S.; Harris, A.J.; Rothery, D.A. A simple explanation for the space-based calculation of lava eruption rates. Earth Planet. Sci. Lett. 2001, 192, 223–233. [Google Scholar] [CrossRef]
- Harris, A.J.L.; Murray, J.B.; Aries, S.E.; Davies, M.A.; Flynn, L.P.; Wooster, M.J.; Wright, R.; Rothery, D.A. Effusion rate trends at Etna and Krafla and their implications for eruptive mechanisms. J. Volcanol. Geotherm. Res. 2000, 102, 237–269. [Google Scholar] [CrossRef]
- Harris, A.; Dehn, J.; Calvari, S. Lava effusion rate definition and measurement: A review. Bull. Volcanol. 2007, 70, 1–22. [Google Scholar] [CrossRef]
- Kilburn, C.R.J.; Pinkerton, H.; Wilson, L. Forecasting the behaviour of lava flows. In Monitoring Active Volcanoes; McGuire, W.J., Kilburn, C.R.J., Murray, J., Eds.; UCL Press: Londin, UK, 1995; pp. 346–368. [Google Scholar]
- Kilburn, C.R.J.; Ballard, R.D. Lava Flows and Flow Fields; Sigurdsson, H., Ed.; Academic Press: San Diego, CA, USA, 2000; pp. 291–305. [Google Scholar]
- Herault, A.; Vicari, A.; Ciraudo, A.; Del Negro, C. Forecasting lava flow hazards during the 2006 Etna eruption: Using the MAGFLOW cellular automata model. Comput. Geosci. 2009, 35, 1050–1060. [Google Scholar] [CrossRef]
- Cappello, A.; Hérault, A.; Bilotta, G.; Ganci, G.; Del Negro, C. MAGFLOW: A physics-based model for the dynamics of lava-flow emplacement. Geol. Soc. Spec. Publ. 2016, 426, 357–373. [Google Scholar] [CrossRef]
- Kereszturi, G.; Cappello, A.; Ganci, G.; Procter, J.; Németh, K.; Del Negro, C.; Cronin, S.J. Numerical simulation of basaltic lava flows in the Auckland Volcanic Field, New Zealand—Implication for volcanic hazard assessment. Bull. Volcanol. 2014, 76, 1–17. [Google Scholar] [CrossRef]
- Del Negro, C.; Cappello, A.; Neri, M.; Bilotta, G.; Hérault, A.; Ganci, G. Lava flow hazards at Mount Etna: Constraints imposed by eruptive history and numerical simulations. Sci. Rep. 2013, 3, 3493. [Google Scholar] [CrossRef]
- Cappello, A.; Geshi, N.; Neri, M.; Del Negro, C. Lava flow hazards—An impending threat at Miyakejima volcano, Japan. J. Volcanol. Geotherm. Res. 2015, 308, 1–9. [Google Scholar] [CrossRef]
- Cappello, A.; Zanon, V.; Del Negro, C.; Ferreira, T.J.; Queiroz, M.G. Exploring lava-flow hazards at Pico Island, Azores Archipelago (Portugal). Terra Nova 2015, 27, 156. [Google Scholar] [CrossRef]
- Pedrazzi, D.; Cappello, A.; Zanon, V.; Del Negro, C. Impact of effusive eruptions from the Eguas–Carvão fissure system, São Miguel Island, Azores Archipelago (Portugal). J. Volcanol. Geotherm. Res. 2015, 291, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Cappello, A.; Ganci, G.; Calvari, S.; Pérez, N.M.; Hernández, P.A.; Silva, S.V.; Cabral, J.; Del Negro, C. Lava flow hazard modeling during the 2014–2015 Fogo eruption, Cape Verde. J. Geophys. Res. Solid Earth 2016, 121, 2290–2303. [Google Scholar] [CrossRef]
- Bilotta, G.; Cappello, A.; Hérault, A.; Vicari, A.; Russo, G.; Del Negro, C. Sensitivity analysis of the MAGFLOW Cellular Automaton model for lava flow simulation. Environ. Model. Softw. 2012, 35, 122–131. [Google Scholar] [CrossRef]
- Bilotta, G.; Cappello, A.; Hérault, A.; Del Negro, C. Influence of topographic data uncertainties and model resolution on the numerical simulation of lava flows. Environ. Model. Softw. 2019, 112, 1–15. [Google Scholar] [CrossRef]
- Rolim, S.B.A.; Grondona, A.; HACKMANN, C.; Rocha, C. A Review of Temperature and Emissivity Retrieval Methods: Applications and Restrictions. Am. J. Environ. Eng. 2016, 6, 119–128. [Google Scholar]
- Sabol, D.E., Jr.; Gillespie, A.R.; Abbott, E.; Yamada, G. Field validation of the ASTER Temperature– Emissivity Separation algorithm. Remote Sens. Environ. 2009, 113, 2328–2344. [Google Scholar] [CrossRef]
- Patrick, M.R.; Dehn, J.; Dean, K. Numerical modeling of lava flow cooling applied to the 1997 Okmok eruption: Approach and analysis. J. Geophys. Res. Solid Earth 2004, 109, B03202. [Google Scholar] [CrossRef]
- Wright, R.; Flynn, L.P. On the retrieval of lava-flow surface temperatures from infrared satellite data. Geology 2003, 31, 893–896. [Google Scholar] [CrossRef]
- Lee, R.J.; Ramsey, M.S.; King, P.L. Development of a new laboratory technique for high-temperature thermal emission spectroscopy of silicate melts. J. Geophys. Res. Solid Earth 2013, 118, 1968–1983. [Google Scholar] [CrossRef] [Green Version]









| MnO | MgO | CaO | LOl | Total | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 48.15 | 1.53 | 16.49 | 11.19 | 0.17 | 5.71 | 10.49 | 3.52 | 1.70 | 0.53 | 0.005 | −0.30 | 99.18 |
| Acquisition Date | Local Time | Eruption Day | Acquisition Time (s) | Cumulative Volume | Time Span (s) | Partial Volume | Daily Effusion Rate |
|---|---|---|---|---|---|---|---|
| 18/07/2001 | 03:00 | 0 | 0 | 0.00 | 0 | 0.00 | 0.00 |
| 18/07/2001 | 13:00 | 1 | 36,000 | 0.37 | 36,000 | 0.37 | 10.28 |
| 19/07/2001 | 16:00 | 2 | 133,200 | 1.70 | 97,200 | 1.33 | 13.68 |
| 20/07/2001 | 13:00 | 3 | 208,800 | 3.50 | 75,600 | 1.80 | 22.81 |
| 22/07/2001 | 11:00 | 5 | 374,400 | 8.58 | 165,600 | 5.08 | 30.68 |
| 26/07/2001 | 12:00 | 9 | 723,600 | 14.98 | 349,200 | 6.40 | 18.33 |
| 28/07/2001 | 16:00 | 11 | 910,800 | 16.99 | 187,200 | 2.01 | 10.74 |
| 30/07/2001 | 11:00 | 13 | 1,065,600 | 18.35 | 154,800 | 1.37 | 8.85 |
| 02/08/2001 | 10:00 | 16 | 1,321,200 | 19.82 | 255,600 | 1.47 | 5.75 |
| 04/08/2001 | 07:00 | 18 | 1,483,200 | 20.62 | 162,000 | 0.80 | 4.94 |
| 06/08/2001 | 11:00 | 20 | 1,670,400 | 21.21 | 187,200 | 0.59 | 3.15 |
| 07/08/2001 | 07:00 | 21 | 1,742,400 | 21.32 | 72,000 | 0.11 | 1.53 |
| 09/08/2001 | 10:00 | 23 | 1,926,000 | 21.40 | 183,600 | 0.08 | 0.44 |
| Length [km] | Area [km2] | Average Thickness [m] | Fitness [ϕ] | |
|---|---|---|---|---|
| Actual lava flow | 6.4 | 1.95 | 11 | - |
| Simulation with ε = 0.8 | 6.9 | 1.94 | 12.4 | 0.76 |
| Simulation with ε = 0.93 | 6.5 | 1.83 | 13.1 | 0.78 |
| Simulation with ε = 1.0 | 6.3 | 1.78 | 13.5 | 0.77 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rogic, N.; Cappello, A.; Ferrucci, F. Role of Emissivity in Lava Flow ‘Distance-to-Run’ Estimates from Satellite-Based Volcano Monitoring. Remote Sens. 2019, 11, 662. https://doi.org/10.3390/rs11060662
Rogic N, Cappello A, Ferrucci F. Role of Emissivity in Lava Flow ‘Distance-to-Run’ Estimates from Satellite-Based Volcano Monitoring. Remote Sensing. 2019; 11(6):662. https://doi.org/10.3390/rs11060662
Chicago/Turabian StyleRogic, Nikola, Annalisa Cappello, and Fabrizio Ferrucci. 2019. "Role of Emissivity in Lava Flow ‘Distance-to-Run’ Estimates from Satellite-Based Volcano Monitoring" Remote Sensing 11, no. 6: 662. https://doi.org/10.3390/rs11060662
APA StyleRogic, N., Cappello, A., & Ferrucci, F. (2019). Role of Emissivity in Lava Flow ‘Distance-to-Run’ Estimates from Satellite-Based Volcano Monitoring. Remote Sensing, 11(6), 662. https://doi.org/10.3390/rs11060662