Mining Deformation Life Cycle in the Light of InSAR and Deformation Models
Abstract
:1. Introduction
1.1. InSAR Deformations
1.2. Subsidence Modelling
1.3. Gaps and Advantages of InSAR and Models
2. Materials and Methods
2.1. Sentinel-1 Data and DInSAR Methodology
2.1.1. DInSAR Processing and Post-Processing
- Step 1: Classical cumulative DInSAR processing,
- Step 2: Quality assessment of the radar signal,
- Step 3: Unification of the results in a common vertical datum by trend removal,
- Step 4: Decomposition from displacement in the direction to the satellite LOS into vertical and horizontal directions, and
- Step 5: Geospatial analysis for extraction of the area affected by the mine subsidence and the lower point of the subsidence trough.
2.1.2. Signal Quality Evaluation
2.1.3. Trend Removal
2.1.4. Three-Dimensional Decomposition
2.1.5. Geospatial and Statistical Analyses
2.2. Deformation Modelling
2.2.1. Generalised Dynamic Subsidence Modelling
2.2.2. Model Application and Parameter Estimation
- –
- subsidence factor: ;
- –
- dispersion parameter of primary mining influences (rock mass parameter): (the angle of draw is about 75°);
- –
- exploitation rim: ;
- –
- time factors describing immediate mining influences: and per year;
- –
- time factors describing residual mining influences: and per year.
2.3. Verification
2.3.1. Time Aggregation
2.3.2. Levelling
3. Case Study
Geological and Mining Conditions in the Area of Interest
4. Results
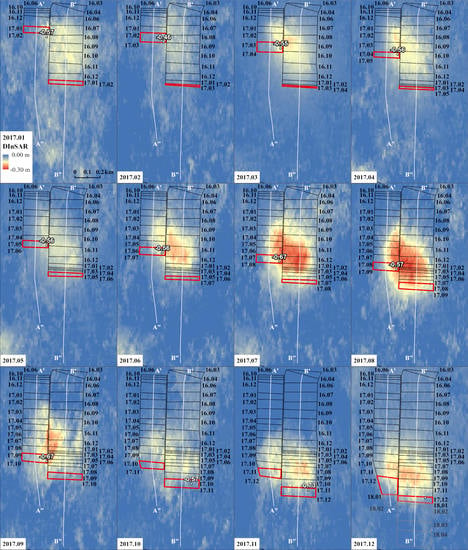
4.1. Cumulative Surface Deformations
4.2. Monthly Deformation
4.3. Verification with Levelling
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zhu, X.; Guo, G.; Zha, J.; Chen, T.; Fang, Q.; Yang, X. Surface dynamic subsidence prediction model of solid backfill mining. Environ. Earth Sci. 2016, 75, 1007. [Google Scholar] [CrossRef]
- Kowalski, A. Deformacje Powierzchni w Górnośląskim Zagłębiu Węglowym [Surface Deformation in the Upper Silesian Coal Basin]; Główny Instytut Górnictwa: Katowice, Poland, 2015; ISBN 978-83-61126-93-5. [Google Scholar]
- Xu, C.-H.; Wang, J.-L.; Jing-Xiang, G.; Wang, J.; Hu, H. Precise point positioning and its application in mining deformation monitoring. Trans. Nonferr. Met. Soc. China 2011, 21, s499–s505. [Google Scholar] [CrossRef] [Green Version]
- Massonnet, D.; Rossi, M.; Carmona, C.; Adragna, F.; Peltzer, G.; Feigl, K.; Rabaute, T. The displacement field of the Landers earthquake mapped by radar interferometry. Nature 1993, 364, 138–142. [Google Scholar] [CrossRef]
- Stramondo, S.; Moro, M.; Doumaz, F.; Cinti, F.R. The 26 December 2003, Bam, Iran earthquake: Surface displacement from Envisat ASAR interferometry. Int. J. Remote Sens. 2005, 26, 1027–1034. [Google Scholar] [CrossRef]
- Samsonov, S.; Tiampo, K. Time series analysis of subsidence at Tauhara and Ohaaki geothermal fields, New Zealand, observed by ALOS PALSAR interferometry during 2007–2009. Can. J. Remote Sens. 2010, 36, S327–S334. [Google Scholar] [CrossRef]
- Yu, B.; Liu, G.; Li, Z.; Zhang, R.; Jia, H.; Wang, X.; Cai, G. Subsidence detection by TerraSAR-X interferometry on a network of natural persistent scatterers and artificial corner reflectors. Comput. Geosci. 2013, 58, 126–136. [Google Scholar] [CrossRef]
- Rucci, A.; Ferretti, A.; Monti Guarnieri, A.; Rocca, F. Sentinel 1 SAR interferometry applications: The outlook for sub millimeter measurements. Remote Sens. Environ. 2012, 120, 156–163. [Google Scholar] [CrossRef]
- Ferretti, A.; Prati, C.; Rocca, F. Nonlinear subsidence rate estimation using permanent scatterers in differential SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2000, 38, 2202–2212. [Google Scholar] [CrossRef]
- Ferretti, A.; Prati, C.; Rocca, F. Permanent scatterers in SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2001, 39, 8–20. [Google Scholar] [CrossRef] [Green Version]
- Ferretti, A.; Fumagalli, A.; Novali, F.; Prati, C.; Rocca, F.; Rucci, A. A new algorithm for processing interferometric data-stacks: SqueeSAR. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3460–3470. [Google Scholar] [CrossRef]
- Berardino, P.; Fornaro, G.; Lanari, R.; Sansosti, E. A new algorithm for surface deformation monitoring based on small baseline differential SAR interferograms. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2375–2383. [Google Scholar] [CrossRef]
- Hooper, A.; Zebker, H.; Segall, P.; Kampes, B. A new method for measuring deformation on volcanoes and other natural terrains using InSAR persistent scatterers. Geophys. Res. Lett. 2004, 31, 1–5. [Google Scholar] [CrossRef]
- Ng, A.H.-M.; Ge, L.; Yan, Y.; Li, X.; Chang, H.-C.; Zhang, K.; Rizos, C. Mapping accumulated mine subsidence using small stack of SAR differential interferograms in the Southern coalfield of New South Wales, Australia. Eng. Geol. 2010, 115, 1–15. [Google Scholar] [CrossRef]
- Crosetto, M.; Monserrat, O.; Cuevas-González, M.; Devanthéry, N.; Crippa, B. Persistent Scatterer Interferometry: A review. ISPRS J. Photogramm. Remote Sens. 2016, 115, 78–89. [Google Scholar] [CrossRef] [Green Version]
- Borecki, M. Ochrona Powierzchni Przed Szkodami Górniczymi [Surface Protection against Mining Damage]; Wydawnictwo Śląsk: Katowice, Poland, 1980; pp. 1–967. [Google Scholar]
- Perski, Z. ERS InSAR data for Geological Interpretation of Mining Subsidence in Upper Silesian Coal Basin in Poland. In Proceedings of the FRINGE’99 2nd International Workshop on SAR Interferometry, Liege, Belgium, 10–12 November 1999. [Google Scholar]
- Jarosz, A.; Karmis, M.; Sroka, A. Subsidence development with time—Experiences from longwall operations in the Appalachian coalfield. Int. J. Min. Geol. Eng. 1990, 8, 261–273. [Google Scholar] [CrossRef]
- Ng, A.H.-M.; Ge, L.; Du, Z.; Wang, S.; Ma, C. Satellite radar interferometry for monitoring subsidence induced by longwall mining activity using Radarsat-2, Sentinel-1 and ALOS-2 data. Int. J. Appl. Earth Obs. Geoinf. 2017, 61, 92–103. [Google Scholar] [CrossRef]
- Przyłucka, M.; Herrera, G.; Graniczny, M.; Colombo, D.; Béjar-Pizarro, M. Combination of conventional and advanced DInSAR to monitor very fast mining subsidence with TerraSAR-X data: Bytom City (Poland). Remote Sens. 2015, 7, 5300–5328. [Google Scholar] [CrossRef]
- Ma, C.; Cheng, X.; Yang, Y.; Zhang, X.; Guo, Z.; Zou, Y. Investigation on mining subsidence based on multi-temporal InSAR and time-series analysis of the small baseline subset—Case study of working faces 22201-1/2 in Bu’ertai mine, Shendong coalfield, China. Remote Sens. 2016, 8, 951. [Google Scholar] [CrossRef]
- Zhou, Y.; Stein, A.; Molenaar, M. Integrating interferometric SAR data with levelling measurements of land subsidence using geostatistics. Int. J. Remote Sens. 2003, 24, 3547–3563. [Google Scholar] [CrossRef]
- Fuhrmann, T.; Caro Cuenca, M.; Knöpfler, A.; Van Leijen, F.J.; Mayer, M.; Westerhaus, M.; Hanssen, R.F.; Heck, B. Combining InSAR, Levelling and GNSS for the Estimation of 3D Surface Displacements; European Space Agency: Paris, France, 2015; Volume SP-731. [Google Scholar]
- Chen, L.; Zhang, L.; Tang, Y.; Zhang, H. Analysis of mining-induced subsidence prediction by exponent Knothe model combined with InSAR and levelling. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2018, IV-3, 53–59. [Google Scholar] [CrossRef]
- Perski, Z. Applicability of ERS-1 and ERS-2 InSAR for land subsidence monitoring in the Silesian coal mining region, Poland. Int. Arch. Photogramm. Remote Sens. 1998, XXXII, 555–558. [Google Scholar]
- Kwiatek, J. Ochrona Obiektów Budowlanych na Terenach Górniczych [Protection of Buildings in Mining Areas]; Wydawnictwo Śląsk: Katowice, Poland, 1997. [Google Scholar]
- Perski, Z.; Jura, D. Identification and measurement of mining subsidence with SAR interferometry: Potentials and limitations. In Proceedings of the 11th International FIG Symposium on Deformation Measurements, Santorini, Greece, 25–28 May 2003. [Google Scholar]
- Blachowski, J.; Milczarek, W.; Stefaniak, P. Deformation information system for facilitating studies of mining-ground deformations, development, and applications. Nat. Hazards Earth Syst. Sci. 2014, 14, 1677–1689. [Google Scholar] [CrossRef] [Green Version]
- Gruszczyński, W.; Niedojadło, Z.; Mrocheń, D. Influence of model parameter uncertainties on forecasted subsidence. Acta Geodyn. Geomater. 2018, 15, 211–228. [Google Scholar] [CrossRef]
- Li, P.; Peng, D.; Tan, Z.; Deng, K. Study of probability integration method parameter inversion by the genetic algorithm. Int. J. Min. Sci. Technol. 2017, 27, 1073–1079. [Google Scholar] [CrossRef]
- Knothe, S. Wpływ czasu na kształtowanie się niecki osiadania [Influence of time on the formation of subsidence trough]. Arch. Górnictwa i Hut. 1953, 1, 51. [Google Scholar]
- Knothe, S. Prognozowanie Wpływów Eksploatacji Górniczej [Forecasting the Impact of Mining Exploitation]; Wydawnictwo Śląsk: Katowice, Poland, 1984. [Google Scholar]
- Kowalski, A. Nieustalone Górnicze Deformacje Powierzchni w Aspekcie Dokładności Prognoz [Dynamic Mining Surface Deformations in the Aspect of Forecast Accuracy]; Głównego Instytutu Górnictwa: Katowice, Poland, 2007. [Google Scholar]
- Yang, Z.F.; Li, Z.W.; Zhu, J.J.; Hu, J.; Wang, Y.J.; Chen, G.L. Analysing the law of dynamic subsidence in mining area by fusing InSAR and leveling measurements. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. ISPRS Arch. 2013, 40, 163–166. [Google Scholar] [CrossRef]
- Iannacone, J.P.; Alessandro, C.; Berti, M.; Morgan, J.; Falorni, G. Characterization of longwall mining induced subsidence by means of automated analysis of InSAR time-series. Eng. Geol. Soc. Territ. 2015, 5, 973–977. [Google Scholar]
- Sun, Q.; Li, Z.W.; Ding, X.L.; Zhu, J.J.; Hu, J. Multi-temporal InSAR data fusion for investigating mining subsidence. In Proceedings of the 2011 International Symposium on Image and Data Fusion, Tengchong, China, 9–11 August 2011. [Google Scholar]
- Coulthard, M.A. Applications of numerical modelling in underground mining and construction. Geotech. Geol. Eng. 1999, 17, 373–385. [Google Scholar] [CrossRef]
- Shahriar, K.; Amoushahi, S.; Arabzadeh, M. Prediction of surface subsidence due to inclined very shallow coal seam mining using FDM. In Proceedings of the Coal Operators’ Conference, Wollongong, Australia, 12–13 February 2009; pp. 130–139. [Google Scholar]
- Rodriguez, E.; Morris, C.S.; Belz, J.E.; Chapin, E.C.; Martin, J.M.; Daffer, W.; Hensley, S. An Assessment of the SRTM Topographic Products; Technical Report JPL D-31639; Jet Propulsion Laboratory: Pasadena, CA, USA, 2005. [Google Scholar]
- Chen, C.W.; Zebker, H.A. Network approaches to two-dimensional phase unwrapping: Intractability and two new algorithms. J. Opt. Soc. Am. A 2000, 17, 401–414. [Google Scholar] [CrossRef]
- Duchon, J. Interpolation des fonctions de deux variables suivant le principe de la flexion des plaques minces [Interpolation of the functions of two variables according to the principle of thin-plate spline]. Revue française d'automatique informatique recherche opérationnelle Analyse numérique 1976, 10, 5–12. [Google Scholar] [CrossRef]
- Thin-Plate Spline Interpolation. Available online: https://doi.org/10.1007/s00190-019-01240-2 (accessed on 27 February 2019).
- Zheng, M.; Deng, K.; Fan, H.; Huang, J. Monitoring and analysis of mining 3D deformation by multi-platform SAR images with the probability integral method. Front. Earth Sci. 2019, 13, 169–179. [Google Scholar] [CrossRef]
- Haghshenas Haghighi, M.; Motagh, M. Sentinel-1 InSAR over Germany: Large-scale interferometry, atmospheric effects, and ground deformation mapping. ZfV-Zeitschrift für Geodäsie Geoinformation und Landmanagement 2017, 142, 245–256. [Google Scholar]
- Jones, E.; Oliphant, E.; Peterson, P. SciPy: Open Source Scientific Tools for Python. Available online: http://www.scipy.org/ (accessed on 16 December 2018).
- Geospatial Data Abstraction Library (GDAL/OGR) Contributors. GDAL/OGR Geospatial Data Abstraction Software Library. Available online: http://gdal.org (accessed on 18 December 2018).
- Gruchlik, P. Zastosowanie Modeli Reologicznych do Opisu Nieustalonych Deformacji Powierzchni [Application of Rheological Models to Describe Dynamic Surface Deformations]; Główny Instytutu Górnictwa: Katowice, Poland, 2003. [Google Scholar]
- Jędrzejec, E. Wersja 5.0 programu Szkody do prognozowania poeksploatacyjnych deformacji górotworu [Version 5.0 of the Szkody programme for forecasting post extraction ground deformation]. WUG Bezpieczeństwo Pracy i Ochrona Środowiska w Górnictwie 2008, 2, 15–19. [Google Scholar]
- World Energy Council: Coal in Poland. Available online: https://www.worldenergy.org/data/resources/country/poland/coal/ (accessed on 29 October 2018).
- Wirth, P. Post-Mining Regions in Central Europe—Problem, Potentials, Possibilities; Wirth, P., Černič Mali, B., Fischner, W., Eds.; Oekom: München, Germany, 2012. [Google Scholar]
- Alves Dias, P.; Kanellopoulos, K.; Medarac, H.; Kapetaki, Z.; Miranda-Barbosa, E.; Shortall, R.; Czako, V.; Telsnig, T.; Vazquez-Hernandez, C.; Lacal Arántegui, R.; et al. EU Coal Regions: Opportunities and Challenges Ahead; European Union: Luxembourg, 2018. [Google Scholar]
- Perski, Z. The interpretation of ERS-1 and ERS-2 InSAR data for the mining subsidence monitoring in Upper Silesian Coal Basin, Poland. Int. Arch. Photogramm. Remote Sens. 2000, XXXIII, 1137–1141. [Google Scholar]
- Volkmer, G. Coal deposits of Poland, including discussion about the degree of peat consolidation during lignite formation. TU Bergakad. Freib. 2006, 1–11. Available online: http://docplayer.net/47498077-Coal-deposits-of-poland-including-discussion-about-the-degree-of-peat-consolidation-during-lignite-formation.html (accessed on 15 January 2019).
- Bekaert, D.P.S.; Walters, R.J.; Wright, T.J.; Hooper, A.J.; Parker, D.J. Statistical comparison of InSAR tropospheric correction techniques. Remote Sens. Environ. 2015, 170, 40–47. [Google Scholar] [CrossRef] [Green Version]
- Yu, C.; Li, Z.; Penna, N.T.; Crippa, P. Generic Atmospheric Correction Model for Interferometric Synthetic Aperture Radar Observations. J. Geophys. Res. Solid Earth 2018, 123, 9202–9222. [Google Scholar] [CrossRef]
- Mróz, M.; Perski, Z. The integration of optical and InSAR data for land subsidence monitoring and its impact on environment of the Upper Silesian Coal Basin. In Proceedings of the Geoinformation for European-Wide Integration, 22nd Symposium of the European Association of Remote Sensing Laboratories, Prague, Czech Republic, 4–6 June 2003; MillPress: Bethlehem, PA, USA; pp. 621–624. [Google Scholar]
- Qu, C.; Shan, X.; Zhao, D.; Zhang, G.; Song, X. Relationships between InSAR Seismic Deformation and Fault Motion Sense, Fault Strike, and Ascending/Descending Modes. Acta Geol. Sin. 2017, 91, 93–108. [Google Scholar] [CrossRef] [Green Version]
- Pagli, C.; Wang, H.; Wright, T.J.; Calais, E.; Lewi, E. Current plate boundary deformation of the Afar rift from a 3-D velocity field inversion of InSAR and GPS. J. Geophys. Res. Solid Earth 2014, 119, 8562–8575. [Google Scholar] [CrossRef] [Green Version]
- Popiołek, E. Ochrona Terenów Górniczych [Protection of Mining Areas]; Wydawnictwo Akademii Górniczo-Hutniczej im. Stanisława Staszica: Warsaw, Poland, 2009; ISBN 978-83-7464-229-3. [Google Scholar]





















| Drawn Line (Profile Lines from Figure 7 in Brackets) | Determined Subsidence Parameters from the Knothe–Budryk Theory | Std of Subsidence Parameters Matching , mm | ||
|---|---|---|---|---|
| Subsidence Factor | Rock Mass Parameter | Exploitation Rim , m | ||
| no 1 (2′-2′′) | 1.13 | 4.5 | 90 | 235 |
| no 2 (1′-1′′) | 1.00 | 3.1 | 90 | 91 |
| no 3 (4′-4′′, 2′-2′′, 6′-6′′) | 1.14 | 2.7 | 50 | 257 |
| no 4 (6′-6′′) | 1.25 | 3.3 | 90 | 86 |
| no 5 (5′-5′′, 6′-6′′, 4′-4′′) | 1.08 | 2.9 | 90 | 281 |
| L-D | 0.89 | -0.04 | 0.183 |
| L-M | 0.85 | 0.20 | 0.388 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ilieva, M.; Polanin, P.; Borkowski, A.; Gruchlik, P.; Smolak, K.; Kowalski, A.; Rohm, W. Mining Deformation Life Cycle in the Light of InSAR and Deformation Models. Remote Sens. 2019, 11, 745. https://doi.org/10.3390/rs11070745
Ilieva M, Polanin P, Borkowski A, Gruchlik P, Smolak K, Kowalski A, Rohm W. Mining Deformation Life Cycle in the Light of InSAR and Deformation Models. Remote Sensing. 2019; 11(7):745. https://doi.org/10.3390/rs11070745
Chicago/Turabian StyleIlieva, Maya, Piotr Polanin, Andrzej Borkowski, Piotr Gruchlik, Kamil Smolak, Andrzej Kowalski, and Witold Rohm. 2019. "Mining Deformation Life Cycle in the Light of InSAR and Deformation Models" Remote Sensing 11, no. 7: 745. https://doi.org/10.3390/rs11070745
APA StyleIlieva, M., Polanin, P., Borkowski, A., Gruchlik, P., Smolak, K., Kowalski, A., & Rohm, W. (2019). Mining Deformation Life Cycle in the Light of InSAR and Deformation Models. Remote Sensing, 11(7), 745. https://doi.org/10.3390/rs11070745