1. Introduction
During a major earthquake, the ground motion can provoke the acoustic resonance between the atmosphere and Earth’s surface. These resonances propagating into the ionosphere can cause oscillations in the ionosphere such as electron density (Ne) and total electron content (TEC). Studies on the acoustic resonance after earthquakes can provide insights on lithosphere-atmosphere-ionosphere coupling and ionospheric anomaly behaviors. The disturbance propagated from the epicenter area after the great Mw = 9.2 Alaska earthquake in 1964 was firstly detected by ionospheric vertical sounding [
1]. Later the analysis of the seismic ionospheric disturbance characteristics provided a new opportunity on earthquake study. Due to the limitation of spatial coverage and resolution of traditional ionospheric monitoring methods [
2,
3], it is difficult to understand well the seismic ionospheric disturbance morphology and the coupling processes between the ground motion and ionospheric dynamics comprehensively.
Since the seismic ionospheric anomalies were first observed through GPS TEC in the California Northridge earthquake in 1994 [
4], a number of studies have been conducted to study coseismic ionospheric disturbances (CIDs) associated with earthquakes. With the increase of continuously operating GPS stations, it provides not only plentiful observations to monitor the pattern and evolution of ionospheric disturbances, but also a great chance to study more details about the coupling between the solid-Earth and atmosphere. The energy released by the earthquake affects the atmosphere in the form of waves of seismic vertical deformation and earthquake-induced tsunami [
5,
6,
7]. Due to the attenuation of atmospheric density, ionospheric disturbances are significantly amplified during the propagation from the ground to the ionosphere [
8]. Ground motion in millimeters per second may cause neutral atmospheric disturbances of a few hundred meters at the ionospheric height [
9,
10]. Different methods are used to study the propagation speed of CIDs and find the source location [
6,
11,
12,
13]. Earthquakes provide unique possibilities to study the response of the ionosphere to earthquakes and better understand the coupling between the solid earth, troposphere, and ionosphere. Strong N-shaped waves following the 2008 Wenchuan earthquake with a plane waveform was found [
14]. In the March 2011 earthquake in Japan, dense TEC disturbances clearly indicated the existence of acoustic-gravity waves generated above the epicenter, the acoustic waves coupled with the Rayleigh waves, and the gravity waves combined with the subsequent tsunami propagation [
6,
15]. High-frequency signals of 3.83 mHz and 5.83 mHz in TEC variations exist only near the epicenter area, which is probably due to attenuation of interference propagation [
6]. Multi-segment structures of seismic faults were detected from high-speed ionospheric GPS data [
16,
17]. The 2012 Mw = 7.8 Haida Gwaii earthquake analyzed and discussed the CIDs propagation characteristics and direction divergence, as well as the correlation and coupling between ionospheric disturbances and ground vertical motion [
18]. Jin [
19] used Plate Boundary Observatory (PBO) GPS observations around the 2005 Northern California offshore earthquake to observe the ionospheric disturbances induced by the earthquake. The southward CIDs following 2015 Mw 7.8 Gorkha, Nepal Earthquake were found to propagate to the F2 region with ~300–440 km captured by COSMIC radio occultation observations [
20,
21].
However, the disturbance directivity and mechanism of the solid, troposphere, and ionosphere coupling remain unclear. Normally, the vertical displacement of the seismic zone plays a more important role in the formation of seismic ionospheric disturbances [
21]. Therefore, earthquakes dominated by strike-slip motion with very small vertical coseismic component are not expected to generate ionospheric perturbations. The relationship between seismic displacement and ionospheric changes has not been fully understood so far [
8,
22,
23]. With no large vertical static coseismic crustal displacements, other seismological parameters such as the magnitude of coseismic horizontal displacements, dimensions of seismic faults and slips at the fault, or a combination of them, may play an important role [
24]. In this paper, the ionospheric disturbances following the 2018 Alaska earthquake dominated by strike-slip motion are investigated from the near-field dense GPS observations and the focal mechanism solutions indicate faulting occurred on a steeply dipping fault striking either west-southwest or north-northwest [
25]. This is the first study on the ionospheric disturbances after the 2018 Alaska earthquake. The data from four instruments were used to analyze the coseismic ionospheric disturbances. The propagation features and directional divergences are investigated and discussed as well as the correlation and coupling between the ionospheric disturbance and ground vertical movement. the regional difference of Rayleigh wave velocity was considered to be one of the important reasons for the diversity of the characteristics of the coseismic ionospheric propagation.
3. Results and Analysis
It is well known that solar and geomagnetic activity can affect the ionosphere.
Figure 3 shows the geomagnetic index Dst, Kp and solar activity index F10.7 for the week around the Alaska earthquake on 23 January 2018. The data of Dst, Kp are available from
http://isgi.unistra.fr/ and the source of solar activity data is
http://data.cma.cn/data/. The Dst index indicates the change in the intensity of the horizontal component of geomagnetism. A value higher than −50 indicates a relatively calm period. The Kp index is used to indicate mid-high latitude geomagnetic activities. Generally, values less than 4 can indicate that the geomagnetic activity is calm. The 10.7 cm solar irradiance reflects the solar activities on a corresponding day and the TEC response to the solar activities is instantaneous [
29]. It can be seen from
Figure 3 that the geomagnetic activity and solar activity on the day of the earthquake are calm. In addition, the data on 23 January of the non-seismic area is used for comparison. Because the geomagnetic and solar activities are calm around the earthquake days, we can conclude that the ionospheric TEC disturbance in the Alaska region was not caused by geomagnetism and solar activity.
In the study, GPS observations were used to analyze the ionospheric response to the Alaska earthquake on 23 January 2018. Since the TEC is an integral parameter, the observed ionospheric disturbance accounts for a large range of altitudes [
24]. However, it is generally assumed that the main contribution to TEC variations appears around the height of the maximum of the ionosphere ionization (F2 layer), with a value of 280 km in this paper. The TEC variations using the filter to eliminate the trend of SIPs motion and ionospheric background changes are most probably related to the earthquake [
30]. Other common ionospheric anomalies basically will not have a correlation between the time and distances. The occurrence time of this disturbance coincides with the earthquake. From
Figure 4, the ionospheric anomalies are detected about 10 min after the main shock. At around 9:43 UTC, the anomalies appeared a few hundred kilometers from the epicenter. The amplitude of the TEC disturbance can reach a magnitude of 0.06 TEC units (TECU, 1 TECU = 10
16 e/m
2). The value of filtered TEC observation turned from positive (
Figure 4c) to negative (
Figure 4d), then turned to positive (
Figure 4f) for the same region as shown in the 09:44 UT and 09:47 UT. The results show that the disturbance is an N-shaped wave and its perturbation period is about 5 min. After 09:52 UT, no TEC disturbance can be detected. Both positive and negative disturbances were detected in the southwest of the epicenter. Compared to the southwest, no disturbance was observed in the northeast.
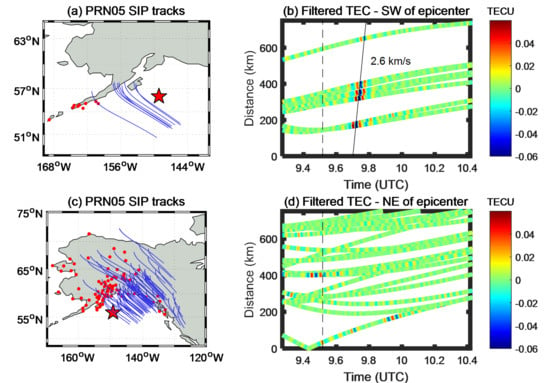
Figure 5 shows an alternate visualization of the ionospheric TEC perturbation after the earthquake. From
Figure 5a,c, it can be seen that the SIP tracks relatively covering the epicenter.
Figure 5b,d are the travel time diagram of the filtered TEC series, which is obtained by taking the time as the
x-axis and
y-axis distance between the SIP tracks and the epicenter as the ordinate. The filtered TEC series is divided into two parts by the SIPs in the southwest and northeast of the epicenter. About ten minutes after the earthquake, it can be seen that the observation in the southwest direction of the epicenter can clearly observe the disturbance with an amplitude of about 0.06 TECU. A linear fitting is performed based on the location of the maximum disturbance which has been shown in
Figure 5b. The propagation velocity of the TEC disturbance can be estimated by the least square fitting, which is about 2.6 km/s, namely, v = ds/dt = (643 km – 148 km)/((9.773 − 9.721) × 3600) ≈ 2.6 km/s, while the observations in the northeast direction have no obvious disturbance in
Figure 5d. This asymmetric disturbance needs to be further studied with more observations in the future, particularly the effect of non-uniform observation geometry [
15].
In order to validate the observation results, the epicenter position is estimated from seismic ionospheric disturbances based on the point source propagation around the epicenter with the estimated horizontal velocity in different directions [
5]. The acoustic waves generated by the earthquake rupture propagate in all directions around the epicenter. It can be approximated that the trajectory of acoustic waves propagating from the ground to the ionosphere is a straight line [
8]. It takes time for the excited acoustic wave propagating from the surface to the ionosphere, as shown in
Figure 6. This wave propagates substantially in the vertical direction [
22]. The acoustic wave propagation formula can be converted by the following equation:
where
R is the Earth radius,
and
are the latitude and longitude of the location of epicenter we want to be obtained,
and
are the latitude and longitude of the location where the disturbances were detected,
is the time of acoustic waves propagating from the surface to the ionosphere,
is the time difference of the earthquake and disturbance,
is the speed of the CIDs.
We brought the disturbance information obtained in
Figure 4 and
Figure 5 into Equation (3) and calculated
and
by the measurement adjustment method. The latitude and longitude of the estimated epicenter location is 55.705° N and 148.773° W. This result is slightly different from the actual epicenter position (56.004° N, 149.166° W). The difference between the actual epicenter and the estimated epicenter is considered reasonable. On the one hand, the source of the disturbance is not strictly located at the center of the earthquake rupture [
31]. On the other hand, the disturbance can shift by several kilometers from its surface location due to vertical variations of the wave speed as well as horizontal winds [
8]. Therefore, combined with the correlation between the disturbance and the location of the epicenter, it can be considered that this CID is caused by the Alaska earthquake.
The bottom pressure values from DART BPRs are corrected for temperature effects and the pressure is converted to an estimated height of the ocean surface above the seafloor by using a constant 670 mm/psia. BPR can record not only the pressure changes caused by sea surface fluctuations but also the vertical movement of the seabed. It is a fact that the deep ocean is an ideal low-pass filter, which allows for Rayleigh waves, tsunamis, and other long-period events to be detected by simply measuring the pressure at a fixed point on the seafloor [
32].
Figure 7 is the detrended sea level change in the vicinity of the epicenter recorded by DART BPRs. The linear trend and constant terms are removed by least squares, leaving only the height change of the sea level. A total of 9 DART BPRs observations within 2000 km were used. The location of the sites is shown in
Figure 1. The BPR series released by DART usually have a tidal report interval of 15 min at rest. When the submarine pressure disturbance is detected, the sampling rate can reach 1 min or 15 s [
32]. The sampling rate of the DART BPR data used in the study is 1 min. Station 46409 is too close to the epicenter, and its seismic impact cannot be regarded as the point source. Therefore, the data of station 46409 was eliminated when fitting. From
Figure 7b, a disturbance at the speed of about 2.7 km/s on the seafloor can be clearly observed on the west of the epicenter, which is consistent with the CIDs propagation velocity detected by the GPS data. There is a significant disturbance within 700 km. As the distance increases, the fluctuation of the vertical data on the ground is significantly reduced. A comparison with the disturbance can indicate that the CID is caused by the wave on the seafloor. On the east of the epicenter, a disturbance at a speed of about 2.0 km/m was observed. Station 46419 and 46407 have disturbances with small amplitudes and the enlarged views, presented in the sub-graphs in
Figure 7d.
Figure 8 shows the correlation between filtered TEC and DART buoy data. The DART station 46403, which is just located below the satellite puncture point as shown in
Figure 8a, is used for the analyses. The black observation in
Figure 8c is the filtered TEC series from station AB02 and the orange line is the copy of the black one shifted 6.7 m in advance. The correlation coefficient between the shifted TEC disturbance series and the vertical ground displacement is 0.74. This shows that the vertical displacement of the ground is very similar to the waveform of the TEC disturbance series. It is expected that the distortion of observed waveforms could be induced by the satellite movement. Fortunately, the radial movement is small when compared to the CID scale in 10 min. For the quasi-radial propagation disturbance, the satellite motion effect was ignored [
18]. The ionospheric disturbance is the same as the waves obtained from BPRs, but it takes a certain time for the excited acoustic wave to propagate from the surface to the ionosphere.
The coseismic horizontal acoustic wave above the focal region is a possible source of the coseismic ionospheric disturbance. It is induced by the refraction of the upward atmospheric pulse due to the vertical neutral density gradient. However, the sound speed at the ionospheric height is around 1 km/s. Therefore, the detected CIDs are mostly related to the Rayleigh wave that propagates with a much higher speed (~3.0–4.5 km/s) [
8,
21]. Note that the locations of CID and DART BPRs are shown in
Figure 5 and
Figure 7, and the 2.6 km/s propagating CID is just above the region where the wave group velocity is about 2.7 km/s. However, other superpositions of acoustic and Rayleigh waves may affect CIDs and make the apparent velocity between the acoustic and Rayleigh waves [
18,
24], which needs to be further investigated with the available data in the future.
The observations from GPS radio occultation measurements were also used to compare them with the ground-based GPS-VTEC observations. In
Figure 9, the radio occultation measurements from Formosat-3/COSMIC are shown. Most of the occultation events last from 300 to 600 s. The ground projection (the blue trajectory) of the occultation points in the COSMIC radio occultation event which starts at 9:48 UTC, is shown in
Figure 9a. The ground projections of the radio occultation points at 08:51 UTC the day before (the red curve) and at 10:25 UTC the day after (the yellow curve) measured at the same position are shown for comparison. In
Figure 9b, ionospheric plasma density perturbations above the earthquake can be observed in the electron density profile of the region from 200 to 500 km. Compared with the observations of the day before and the day after, the electron density after the earthquake is significantly smaller. In the case of ruling out the influence of solar and geomagnetic activities, the phenomenon of a significant decrease in electron density is considered to be caused by the earthquake. A moving average filter was used to extract trend items during data processing [
21]. The observation accuracy of the cosmic electron density data is on the order of 10 cubic degrees. From
Figure 9c, it can be clearly seen that the detrended data on the 23rd January is much larger than the data on the 22nd and 24th January, and its magnitude also indicates that this is not caused by the observation error. It can be observed that at the height where the electron density (250 km–350 km) is larger, the amplitude of this COSMIC disturbance is more obvious.
COSMIC radio occultation data with observations from ground-based GPS stations were combined from
Figure 10. Since the TEC and electron density are not a single linear relationship, the perturbed waveforms cannot be compared. Thus, the waveform data shown in
Figure 10 are normalized by the maximum amplitude. The time of the perturbation coincides with the propagation distance which is very similar to the TEC observations. These results indicate that the wave has reached about 300 km altitude and indeed causes changes in the vertical structure of the ionosphere. The results of
Figure 10 support the conclusion that the perturbation of electron density is not an error but is probably caused by the earthquake. The vertical ground motions from the observations of 91 broadband seismographers are presented in
Figure 11. The vertical component in the east and west directions are shown in
Figure 11b,d, respectively. It can be observed that the Rayleigh waves propagated in all directions. Based on the arrival times of the Rayleigh waves at stations with different distances, the group velocity of the surface Rayleigh wave is estimated to be approximately 3.8 km/s in the west and 3.9 km/s in the east directions. It should be pointed out that the Rayleigh wave appearance epoch is almost at the onset of the earthquake according to the linear fitting estimation. Not only the Rayleigh wave propagation speed at the surface is different, but the vertical ground motions are also observed to be different. This observation is related to the fact that the Alaska earthquake occurred as the result of strike-slip faulting within the shallow lithosphere of the Pacific plate [
24]. Focal mechanism solutions indicate that faulting occurred on a steeply dipping fault striking either west-southwest or north-northwest. The first apparent motion observed on the west side is positive while the first one on the east side is negative. Since not enough GPS observations are available to see the ionospheric disturbances over the Alaska region, it is unlikely to make a comparative analysis at present. The Rayleigh wave-induced CID at such a speed is possible [
23]. It is believed that the anisotropy of the Rayleigh wave could be an important source of CID propagation divergence in different directions [
18].
The TEC perturbation time series obtained from GPS dual-frequency observations can be used to analyze the amplitude, duration and propagation velocity of the disturbance. However, the time domain analysis can only reflect the change of the amplitude of the signal, so the frequency domain analysis of the disturbance is performed by using the fast Fourier transform (FFT). In
Figure 12, the disturbance series extracted from the observations are shown on the left, and on the right is the spectrum distribution obtained by Fourier transform. The moment when the disturbance occurs can be clearly observed from
Figure 12. The power spectrum peak at the corresponding time is also obvious. In
Figure 12b, the TEC series of the station AV02 were analyzed and the corresponding frequency of the power extremum was 6.1 mHz.
Figure 12d shows the frequency of vertical ground motions from DART BRP which has a corresponding frequency of the power extremum of 5.8 mHz. From
Figure 12b,d, the perturbation frequency of the CIDs observed by the GPS satellite is similar to the BPRs data. Combining the conclusions obtained in
Figure 8, it can be considered that there is a strong similarity between the two disturbances. The coseismic ionospheric effect is a result of the upward propagation acoustic wave induced by the Rayleigh wave rather than the direct effect of the focal rupture [
33]. While
Figure 12f shows the frequency of vertical ground motions from seismographers N19K (60.813° N, 154.484° W) with a center of 8.1 mHz. It can be seen from this figure that the power enhances significantly with the arrival of large amplitude surface Rayleigh waves. Combined with the velocity of the dispersion map and the perturbation fit [
22], it can be determined that this perturbation is an ionospheric disturbance caused by Rayleigh waves. The frequency of the wave observed by the seismometers is greater than the waves obtained from DART stations and GPS receivers. This also proves that the detected CIDs are mostly related to the Rayleigh wave for another point of view [
6].