Exploring the Influence of Spatial Resolution on the Digital Mapping of Soil Organic Carbon by Airborne Hyperspectral VNIR Imaging
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area and Soil Samples
2.2. Airborne Hyperspectral Images
2.3. The Prediction Models
2.4. Evaluation Indices
3. Results
3.1. Descriptive Statistics of SOC
3.2. Resampled Hyperspectral Reflectance
3.3. SOC Predictions
4. Discussion
4.1. Influential Factors in Predicting SOC
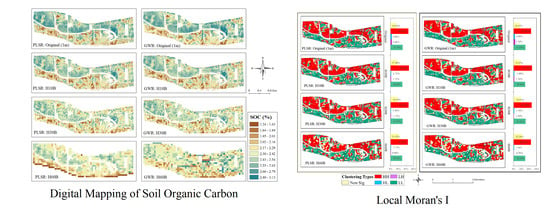
4.2. Spatial Autocorrelation of SOC at Different Spatial Scales
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lal, R. Global potential of soil carbon sequestration to mitigate the greenhouse effect. Crit. Rev. Plant Sci. 2003, 22, 151–184. [Google Scholar] [CrossRef]
- Arnold, R.W. Role of soil survey in obtaining a global carbon budget. Soils Glob. Chang. 1995, 21, 257–263. [Google Scholar]
- Kempen, B.; Brus, D.J.; Stoorvogel, J.J.; Heuvelink, G.; de Vries, F. Efficiency comparison of conventional and digital soil mapping for updating soil maps. Soil Sci. Soc. Am. J. 2012, 76, 2097–2115. [Google Scholar] [CrossRef]
- Forkuor, G.; Hounkpatin, O.K.; Welp, G.; Thiel, M. High resolution mapping of soil properties using remote sensing variables in south-western Burkina Faso: A comparison of machine learning and multiple linear regression models. PloS ONE 2017, 12, e0170478. [Google Scholar] [CrossRef]
- Zeraatpisheh, M.; Ayoubi, S.; Jafari, A.; Tajik, S.; Finke, P. Digital mapping of soil properties using multiple machine learning in a semi-arid region, central Iran. Geoderma 2019, 338, 445–452. [Google Scholar] [CrossRef]
- Davidson, E.A.; Janssens, I.A. Temperature sensitivity of soil carbon decomposition and feedbacks to climate change. Nature 2006, 440, 165–173. [Google Scholar] [CrossRef] [Green Version]
- Adamchuk, V.I.; Allred, B.; Doolittle, J.; Grote, K.; Rossel, R.; Ditzler, C.; West, L. Tools for proximal soil sensing. In Soil Survey Manua; Ditzler, C., West, L., Eds.; U.S. Department of Agriculture: Lincoln, NE, USA, 2015; Volume 6, pp. 1–31. [Google Scholar]
- Viscarra Rossel, R.A.; Webster, R.; Bui, E.N.; Baldock, J.A. Baseline map of organic carbon in Australian soil to support national carbon accounting and monitoring under climate change. Glob. Chang. Biol. 2014, 20, 2953–2970. [Google Scholar] [CrossRef] [Green Version]
- Dhawale, N.M.; Adamchuk, V.I.; Prasher, S.O.; Rossel, R.A.V.; Ismail, A.A.; Whalen, J.K.; Louargant, M. Comparing Visible/NIR and MIR Hyperspectrometry for Measuring Soil Physical Properties. In Proceedings of the International Conference of American Society of Biological Engineers, Montreal, QC, Canada, 13–16 July 2014; American Society of Agricultural and Biological Engineers: Saint Joseph, MI, USA, 2014. [Google Scholar] [CrossRef]
- Terra, F.S.; Rossel, R.A.V.; Demattê, J.A. Spectral fusion by Outer Product Analysis (OPA) to improve predictions of soil organic C. Geoderma 2019, 335, 35–46. [Google Scholar] [CrossRef]
- Hobley, E.U.; Prater, I. Estimating soil texture from vis–NIR spectra. Eur. J.Soil Sci. 2019, 70, 83–95. [Google Scholar] [CrossRef]
- Kawamura, K.; Tsujimoto, Y.; Nishigaki, T.; Andriamananjara, A.; Rabenarivo, M.; Asai, H.; Rakotoson, T.; Razafimbelo, T. Laboratory Visible and Near-Infrared Spectroscopy with Genetic Algorithm-Based Partial Least Squares Regression for Assessing the Soil Phosphorus Content of Upland and Lowland Rice Fields in Madagascar. Remote Sens. 2019, 11, 506. [Google Scholar] [CrossRef]
- Shi, T.Z.; Chen, Y.Y.; Liu, H.Z.; Wang, J.J.; Wu, G.F. Soil Organic Carbon Content Estimation with Laboratory-Based Visible-Near-Infrared Reflectance Spectroscopy: Feature Selection. Appl. Spectrosc. 2014, 68, 831–837. [Google Scholar] [CrossRef] [PubMed]
- Viscarra Rossel, R.A.; Webster, R. Predicting soil properties from the Australian soil visible-near infrared spectroscopic database. Eur. J. Soil Sci. 2012, 63, 848–860. [Google Scholar] [CrossRef]
- Fang, Q.; Hong, H.; Zhao, L.; Kukolich, S.; Yin, K.; Wang, C. Visible and near-infrared reflectance spectroscopy for investigating soil mineralogy: a review. J. Spectrosc. 2018, 2018, 14. [Google Scholar] [CrossRef]
- Cambou, A.; Cardinael, R.; Kouakoua, E.; Villeneuve, M.; Durand, C.; Barthes, B.G. Prediction of soil organic carbon stock using visible and near infrared reflectance spectroscopy (VNIRS) in the field. Geoderma 2016, 261, 151–159. [Google Scholar] [CrossRef]
- Ji, W.J.; Shi, Z.; Huang, J.Y.; Li, S. In Situ Measurement of Some Soil Properties in Paddy Soil Using Visible and Near-Infrared Spectroscopy. PLoS ONE 2014, 9, 11. [Google Scholar] [CrossRef]
- Gopal, B.; Shetty, A.; Ramya, B.J. Prediction of the presence of topsoil nitrogen from spaceborne hyperspectral data. Geocarto Int. 2015, 30, 82–92. [Google Scholar] [CrossRef]
- Goetz, A.F.H. Three decades of hyperspectral remote sensing of the Earth: A personal view. Remote Sens. Environ. 2009, 113, S5–S16. [Google Scholar] [CrossRef]
- Gomez, C.; Rossel, R.A.V.; McBratney, A.B. Soil organic carbon prediction by hyperspectral remote sensing and field vis-NIR spectroscopy: An Australian case study. Geoderma 2008, 146, 403–411. [Google Scholar] [CrossRef]
- Stevens, A.; Miralles, I.; Wesemael, B.V. Soil Organic Carbon Predictions by Airborne Imaging Spectroscopy: Comparing Cross-Validation and Validation. Soil Sci. Soc. Am. J. 2012, 76, 2174–2183. [Google Scholar] [CrossRef]
- Peon, J.; Fernandez, S.; Recondo, C.; Calleja, J.F. Evaluation of the spectral characteristics of five hyperspectral and multispectral sensors for soil organic carbon estimation in burned areas. Int. J. Wildland Fire 2017, 26, 230–239. [Google Scholar] [CrossRef]
- Hestir, E.L.; Khanna, S.; Andrew, M.E.; Santos, M.J.; Viers, J.H.; Greenberg, J.A.; Rajapakse, S.S.; Ustin, S.L. Identification of invasive vegetation using hyperspectral remote sensing in the California Delta ecosystem. Remote Sens. Environ. 2008, 112, 4034–4047. [Google Scholar] [CrossRef]
- Viscarra Rossel, R.A.; McGlynn, R.N.; McBratney, A.B. Determining the composition of mineral-organic mixes using UV-vis-NIR diffuse reflectance spectroscopy. Geoderma 2006, 137, 70–82. [Google Scholar] [CrossRef]
- Viscarra Rossel, R.; Behrens, T.J.G. Using data mining to model and interpret soil diffuse reflectance spectra. Geoderma 2010, 158, 46–54. [Google Scholar] [CrossRef]
- Liu, Y.; Pan, X.; Wang, C.; Li, Y.; Shi, R. Predicting Soil Salinity with Vis–NIR Spectra after Removing the Effects of Soil Moisture Using External Parameter Orthogonalization. PLoS ONE 2015, 10, e0140688. [Google Scholar] [CrossRef] [PubMed]
- Lagacherie, P.; Sneep, A.-R.; Gomez, C.; Bacha, S.; Coulouma, G.; Hamrouni, M.H.; Mekki, I. Combining Vis–NIR hyperspectral imagery and legacy measured soil profiles to map subsurface soil properties in a Mediterranean area (Cap-Bon, Tunisia). Geoderma 2013, 209, 168–176. [Google Scholar] [CrossRef]
- Gupta, A.; Vasava, H.B.; Das, B.S.; Choubey, A.K. Local modeling approaches for estimating soil properties in selected Indian soils using diffuse reflectance data over visible to near-infrared region. Geoderma 2018, 325, 59–71. [Google Scholar] [CrossRef]
- Farrukh, N. Evaluation of the eo-1heperion Image for Assessment of Soil Organic Carbon in Faizabad Watershed. Master’s Thesis, University of Central Asia, Kyrgyz Republic, 2011. [Google Scholar]
- Dotto, A.C.; Diniz Dalmolin, R.S.; ten Caten, A.; Grunwald, S. A systematic study on the application of scatter-corrective and spectral-derivative preprocessing for multivariate prediction of soil organic carbon by Vis-NIR spectra. Geoderma 2018, 314, 262–274. [Google Scholar] [CrossRef]
- Vasat, R.; Kodesova, R.; Boruvka, L. Ensemble predictive model for more accurate soil organic carbon spectroscopic estimation. Comput. Geosci. 2017, 104, 75–83. [Google Scholar] [CrossRef]
- Tekin, Y.; Tumsavas, Z.; Mouazen, A.M. Comparing the artificial neural network with parcial least squares for prediction of soil organic carbon and PH at different moisture content levels using visible and near-infrared spectroscopy. Revista Brasileira de Ciência do Solo 2014, 38, 1794–1804. [Google Scholar] [CrossRef]
- Kumar, S.; Lal, R.; Liu, D. A geographically weighted regression kriging approach for mapping soil organic carbon stock. Geoderma 2012, 189, 627–634. [Google Scholar] [CrossRef]
- Guo, L.; Zhao, C.; Zhang, H.; Chen, Y.; Linderman, M.; Zhang, Q.; Liu, Y. Comparisons of spatial and non-spatial models for predicting soil carbon content based on visible and near-infrared spectral technology. Geoderma 2017, 285, 280–292. [Google Scholar] [CrossRef]
- Lee, C.M.; Cable, M.L.; Hook, S.J.; Green, R.O.; Ustin, S.L.; Mandl, D.J.; Middleton, E.M. An introduction to the NASA Hyperspectral InfraRed Imager (HyspIRI) mission and preparatory activities. Remote Sens. Environ. 2015, 167, 6–19. [Google Scholar] [CrossRef]
- Ben-Dor, E.; Kafri, A.; Varacalli, G. SHALOM: An Italian–Israeli hyperspectral orbital mission—Update. In Proceedings of the International Geoscience and Remote Sensing Symposium, Quebec City, QC, Canada, 13–18 July 2014. [Google Scholar]
- Deng, S.; Tian, L.; Jian, L.I.; Chen, X.; Sun, Z.; Zhang, L.; Wei, A. A novel chlorophyll-a inversion model in turbid water for GF-5 satellite hyperspectral sensor—A case in Poyang Lake. J. Cent. China Normal Univ. 2018, 03, 409–415. [Google Scholar]
- Gomez, C.; Oltra-Carrio, R.; Bacha, S.; Lagacherie, P.; Briottet, X. Evaluating the sensitivity of clay content prediction to atmospheric effects and degradation of image spatial resolution using Hyperspectral VNIR/SWIR imagery. Remote Sens. Environ. 2015, 164, 1–15. [Google Scholar] [CrossRef]
- Shi, C.; Wang, L. Incorporating spatial information in spectral unmixing: A review. Remote Sens. Environ. 2014, 149, 70–87. [Google Scholar] [CrossRef]
- Griffith, D.A.; Chun, Y. Spatial Autocorrelation and Uncertainty Associated with Remotely-Sensed Data. Remote Sens. 2016, 8, 535. [Google Scholar] [CrossRef]
- Chen, S.; Feng, L.; Li, S.; Ji, W.; Shi, Z. Vis-NIR spectral inversion for prediction of soil total nitrogencontent in laboratory based on locally weighted regression. Acta Pedol. Sin. 2015, 52, 312–320. [Google Scholar]
- Heil, J.; Häring, V.; Marschner, B.; Stumpe, B. Advantages of fuzzy k-means over k-means clustering in the classification of diffuse reflectance soil spectra: A case study with West African soils. Geoderma 2019, 337, 11–21. [Google Scholar] [CrossRef]
- Chen, T.; CHANG, Q.-R.; Liu, J. Study of spatial interpolation of soil cd contents in sewage irrigated area based on soil spectral information assistance. Spectrosc. Spectr. Anal. 2013, 33, 2157–2162. [Google Scholar]
- Burt, R.; Staff, S. Kellogg soil survey laboratory methods manual. In Natural Resources Conservation Services; National Soil Survey Center: Lincoln, NE, USA, 2014. [Google Scholar]
- ISO10694, ISO. Soil Quality—Determination of Organic and Total Carbon After Dry Combustion (Elementary Analysis); ISO: Geneva, Switzerland, 1995. [Google Scholar]
- Ross, S.M. Peirce’s criterion for the elimination of suspect experimental data. J. Eng. Technol. 2003, 20, 38–41. [Google Scholar]
- Guo, L.; Zhang, H.; Shi, T.; Chen, Y.; Jiang, Q.; Linderman, M. Prediction of soil organic carbon stock by laboratory spectral data and airborne hyperspectral images. Geoderma 2019, 337, 32–41. [Google Scholar] [CrossRef]
- Guo, L.; Linderman, M.; Shi, T.Z.; Chen, Y.Y.; Duan, L.J.; Zhang, H.T. Exploring the Sensitivity of Sampling Density in Digital Mapping of Soil Organic Carbon and Its Application in Soil Sampling. Remote Sens. 2018, 10, 888. [Google Scholar] [CrossRef]
- Lehmann, T.M.; Gonner, C.; Spitzer, K. Survey: Interpolation methods in medical image processing. IEEE Trans. Med. Imaging 1999, 18, 1049–1075. [Google Scholar] [CrossRef]
- Schultz, R.R.; Stevenson, R.L. Extraction of high-resolution frames from video sequences. IEEE Trans. Image Process. 1996, 5, 996–1011. [Google Scholar] [CrossRef]
- Keys, R.G. Cubic convolution interpolation for digital image-processing. IEEE Trans. Acoust. Speech Signal Process. 1981, 29, 1153–1160. [Google Scholar] [CrossRef]
- Geladi, P.; Kowalski, B.R. Partial least-squares regression: a tutorial. Anal. Chim. Acta 1986, 185, 1–17. [Google Scholar] [CrossRef]
- Askari, M.S.; O’Rourke, S.M.; Holden, N.M. Evaluation of soil quality for agricultural production using visible-near-infrared spectroscopy. Geoderma 2015, 243, 80–91. [Google Scholar] [CrossRef]
- Xu, L.; He, N.P.; Yu, G.R. Methods of evaluating soil bulk density: Impact on estimating large scale soil organic carbon storage. Catena 2016, 144, 94–101. [Google Scholar] [CrossRef] [Green Version]
- Harald, M.; Paul, G. Multivariate calibration. Technometrics 1991, 1158, 61. [Google Scholar]
- Brunsdon, C.; Fotheringham, S.; Charlton, M. Geographically weighted regression. J. R. Stat. Soc. Ser. D (The Statistician) 1998, 47, 431–443. [Google Scholar] [CrossRef]
- Charlton, M.; Fotheringham, S.; Brunsdon, C. Geographically weighted regression. In White Paper. National Centre for Geocomputation; National University of Ireland Maynooth: Maynooth, Ireland, 2009. [Google Scholar]
- Fotheringham, A.S.; Brunsdon, C.; Charlton, M. Geographically Weighted Regression; Wiley: New York, NY, USA, 2002. [Google Scholar]
- Gogé, F.; Gomez, C.; Jolivet, C.; Joffre, R. Which strategy is best to predict soil properties of a local site from a national Vis–NIR database? Geoderma 2014, 213, 1–9. [Google Scholar] [CrossRef]
- Bellon-Maurel, V.; Fernandez-Ahumada, E.; Palagos, B.; Roger, J.-M.; McBratney, A. Critical review of chemometric indicators commonly used for assessing the quality of the prediction of soil attributes by NIR spectroscopy. TrAC Trends Anal. Chem. 2010, 29, 1073–1081. [Google Scholar] [CrossRef]
- Li, D.; Chen, Y. Computer and Computing Technologies in Agriculture: 5th IFIP TC 5, SIG 5.1 International Conference, CCTA 2011, Beijing, China, 29–31 October 2011, Proceedings; Springer Science & Business Media: Berlin, Germany, 2012. [Google Scholar]
- Landgrebe, D.A. Signal Theory Methods in Multispectral Remote Sensing; John Wiley & Sons: Hoboken, NJ, USA, 2005; Volume 29. [Google Scholar]
- Schowengerdt, R.A. Remote Sensing: Models and Methods for Image Processing; Academic Press: Cambridge, MA, USA, 2006. [Google Scholar]
- Castaldi, F.; Palombo, A.; Santini, F.; Pascucci, S.; Pignatti, S.; Casa, R. Evaluation of the potential of the current and forthcoming multispectral and hyperspectral imagers to estimate soil texture and organic carbon. Remote Sens. Environ. 2016, 179, 54–65. [Google Scholar] [CrossRef]
- Hunt, G.R. Near-infrared (1.3–2.4) μm spectra of alteration minerals—Potential for use in remote sensing. Geophysics 1979, 44, 1974–1986. [Google Scholar] [CrossRef]
- Plaza, A. Near real-time endmember extraction from remotely sensed hyperspectral data using NVidia GPUs. In Real-Time Image and Video Processing 2010; International Society for Optics and Photonics: San Diego, CA, USA, 2010; Volume 7724, p. 772409. [Google Scholar]
- Wold, S.; Johansson, E.; Cocchi, M. Partial Least Squares Projections to Latent Structures; Wiley & Sons: Hoboken, NJ, USA, 2002. [Google Scholar]
- Liu, Y.; Guo, L.; Jiang, Q.; Zhang, H.; Chen, Y. Comparing geospatial techniques to predict SOC stocks. Soil Tillage Res. 2015, 148, 46–58. [Google Scholar] [CrossRef]
- Yoon, T.K.; Noh, N.J.; Han, S.; Kwak, H.; Lee, W.K.; Son, Y. Small-scale spatial variability of soil properties in a Korean swamp. Landsc. Ecol. Eng. 2015, 11, 303–312. [Google Scholar] [CrossRef]







| Number | Range (%) | Minimum (%) | Maximum (%) | Mean (%) | S.D. (%) | Skewness | CV | C0/(C0 + C) | |
|---|---|---|---|---|---|---|---|---|---|
| Calibration | 120 | 1.84 | 1.31 | 3.14 | 2.34 | 0.38 | −0.65 | 16.05% | 59.46% |
| Validation | 61 | 1.55 | 1.43 | 2.98 | 2.40 | 0.28 | −0.93 | 11.79% | 41.84% |
| Whole | 181 | 1.84 | 1.31 | 3.14 | 2.36 | 0.35 | 0.74 | 14.72% | 58.62% |
| PLSR | GWR | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Num.LVs | RMSEC | RMSEP | R2C | R2P | RPIQ | RMSEC | RMSEP | R2C | R2P | RPIQ | |
| Original | 4 | 0.165 | 0.159 | 0.797 | 0.708 | 1.957 | 0.138 | 0.155 | 0.857 | 0.814 | 2.003 |
| H10B | 4 | 0.181 | 0.183 | 0.754 | 0.609 | 1.697 | 0.16 | 0.171 | 0.807 | 0.802 | 1.813 |
| H10C | 4 | 0.184 | 0.194 | 0.747 | 0.559 | 1.603 | 0.163 | 0.181 | 0.801 | 0.793 | 1.713 |
| H10N | 4 | 0.18 | 0.196 | 0.759 | 0.551 | 1.583 | 0.160 | 0.186 | 0.808 | 0.788 | 1.667 |
| H30B | 5 | 0.226 | 0.222 | 0.617 | 0.45 | 1.400 | 0.220 | 0.216 | 0.639 | 0.646 | 1.435 |
| H30C | 5 | 0.227 | 0.232 | 0.613 | 0.406 | 1.342 | 0.223 | 0.227 | 0.630 | 0.638 | 1.366 |
| H30N | 5 | 0.235 | 0.250 | 0.587 | 0.33 | 1.242 | 0.228 | 0.246 | 0.611 | 0.607 | 1.260 |
| H60B | 6 | 0.259 | 0.267 | 0.497 | 0.382 | 1.166 | 0.247 | 0.267 | 0.543 | 0.497 | 1.161 |
| H60C | 6 | 0.260 | 0.270 | 0.494 | 0.381 | 1.151 | 0.250 | 0.267 | 0.533 | 0.502 | 1.161 |
| H60N | 6 | 0.257 | 0.274 | 0.505 | 0.417 | 1.134 | 0.237 | 0.273 | 0.578 | 0.535 | 1.136 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, L.; Shi, T.; Linderman, M.; Chen, Y.; Zhang, H.; Fu, P. Exploring the Influence of Spatial Resolution on the Digital Mapping of Soil Organic Carbon by Airborne Hyperspectral VNIR Imaging. Remote Sens. 2019, 11, 1032. https://doi.org/10.3390/rs11091032
Guo L, Shi T, Linderman M, Chen Y, Zhang H, Fu P. Exploring the Influence of Spatial Resolution on the Digital Mapping of Soil Organic Carbon by Airborne Hyperspectral VNIR Imaging. Remote Sensing. 2019; 11(9):1032. https://doi.org/10.3390/rs11091032
Chicago/Turabian StyleGuo, Long, Tiezhu Shi, Marc Linderman, Yiyun Chen, Haitao Zhang, and Peng Fu. 2019. "Exploring the Influence of Spatial Resolution on the Digital Mapping of Soil Organic Carbon by Airborne Hyperspectral VNIR Imaging" Remote Sensing 11, no. 9: 1032. https://doi.org/10.3390/rs11091032
APA StyleGuo, L., Shi, T., Linderman, M., Chen, Y., Zhang, H., & Fu, P. (2019). Exploring the Influence of Spatial Resolution on the Digital Mapping of Soil Organic Carbon by Airborne Hyperspectral VNIR Imaging. Remote Sensing, 11(9), 1032. https://doi.org/10.3390/rs11091032