Cross-Comparison and Methodological Improvement in GPS Tomography
Abstract
:1. Potential of GPS Tomography for Meteorological Applications
2. Overview of the Selected Severe Weather Situation
3. GPS Data and External Observations
3.1. Data Inputs for GPS Tomography Using the Continuously Operating Reference Station (CORS) Network
3.2. Independent Observations of Water Vapour Density and Wet Refractivity Profiles
3.2.1. Profiles from Radiosonde
3.2.2. Profiles from the Radio-Occultation Technique
4. A Selection of Five Tomography Models
5. Methodological Improvement in GNSS Tomography
5.1. Methodology for Improving of the Geometrical Representativeness
5.1.1. Data Stacking of Slant Observations
5.1.2. Use of Pseudo-Slant Observations
5.2. A Priori Condition and Improvement of the Convergence in the Inversion Process
5.3. Sensitivity Tests Based on the Uncertainty of Slant Observations
6. Results of Methodological Improvement in GPS Tomography
6.1. Results Regarding the Improvement of Geometrical Distribution
6.1.1. Interest in Data Stacking for Mid-Troposphere Retrievals
6.1.2. Interest in Pseudo-Slant Observations for Low- and Mid-Troposphere Retrievals
6.2. Convergence of Tomography Solutions with Respect to A Priori Conditions and Time Resolution of Processes
6.3. Results Regarding the Impact on the Precision of Slant Retrievals
7. Cross-Comparison of Tomography Models with Profiles from External Observations
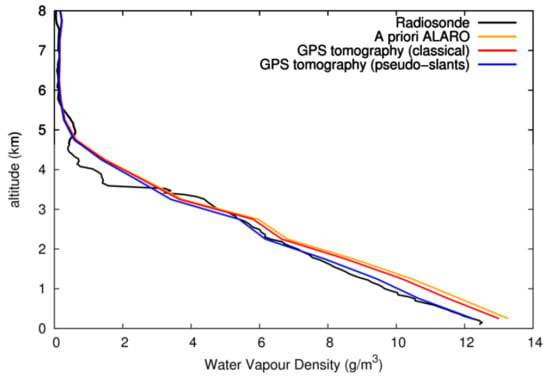
7.1. Comparison with Profiles from Radiosondes
7.2. Comparison with Profiles from Radio-Occultations
7.3. Selected Results–Focus on Tomography Network in the East and during Selected Epochs
8. Summary, Conclusions, and Perspectives for Future Works
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Overview of the BIRA Tomography Model
Appendix B. Overview of the WUELS Tomography Model
Appendix C. Overview of the VSB Tomography Model
Appendix D. Overview of the TUW Tomography Model
Appendix E. Overview of the UBI Tomography Model
References
- Flores, A.; Ruffini, G.; Rius, A. 4D tropospheric tomography using GPS slant wet delays. Ann. Geophys. 2000, 18, 223–234. [Google Scholar] [CrossRef]
- Seko, H.; Shimada, S.; Nakamura, H.; Kato, T. Three-dimensional distribution of water vapor estimated from tropospheric delay of GPS data in a mesoscale precipitation system of the Baiu front. Earth Planets Space 2000, 52, 927–933. [Google Scholar] [CrossRef] [Green Version]
- Elgered, G.; Davis, J.L.; Herring, T.A.; Shapiro, I.I. Geodesy by radio interferometry: Water vapor radiometry for estimation of the wet delay. J. Geophys. Res. Solid Earth 1991, 96, 6541–6555. [Google Scholar] [CrossRef]
- Gradinarsky, L. Sensing Atmospheric Water Vapor Using Radio Waves: Studies of the 2, 3 and 4-D Structure of the Atmospheric Water Vapor Using Ground-based Radio Techniques Comprising the Global Positioning System, Microwave Radiometry and Very Long Baseline Interferometr; Chalmers University of Technology: Gothenburg, Sweden, 2002. [Google Scholar]
- Gradinarsky, L.; Jarlemark, P. Ground-Based GPS Tomography of Water Vapor: Analysis of Simulated and Real Data. J. Meteorol. Soc. Jpn. 2004, 82, 551–560. [Google Scholar] [CrossRef] [Green Version]
- Champollion, C.; Masson, F.; Bouin, M.-N.; Walpersdorf, A.; Doerflinger, E.; Bock, O.; Van Baelen, J. GPS water vapour tomography: Preliminary results from the ESCOMPTE field experiment. Atmos. Res. 2005, 74, 253–274. [Google Scholar] [CrossRef] [Green Version]
- Bastin, S. On the use of GPS tomography to investigate water vapor variability during a Mistral/sea breeze event in southeastern France. Geophys. Res. Lett. 2005, 32, L05808. [Google Scholar] [CrossRef] [Green Version]
- Bastin, S.; Champollion, C.; Bock, O.; Drobinski, P.; Masson, F. Diurnal cycle of water vapor as documented by a dense GPS network in a coastal area during ESCOMPTE IOP2. J. Appl. Meteorol. Clim 2007, 46, 167–187. [Google Scholar] [CrossRef] [Green Version]
- Troller, M.; Geiger, A.; Brockmann, E.; Bettems, J.-M.; Bürki, B.; Kahle, H.-G. Tomographic determination of the spatial distribution of water vapor using GPS observations. Adv. Space Res. 2006, 37, 2211–2217. [Google Scholar] [CrossRef]
- Nilsson, T.; Gradinarsky, L. Water vapor tomography using GPS phase observations: Simulation results. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2927–2941. [Google Scholar] [CrossRef]
- Nilsson, T.; Elgered, G. Water vapour tomography using GPS phase observations: Results from the ESCOMPTE experiment. Tellus A Dyn. Meteorol. Oceanogr. 2007, 59, 674–682. [Google Scholar] [CrossRef] [Green Version]
- Boniface, K.; Ducrocq, V.; Jaubert, G.; Yan, X.; Brousseau, P.; Masson, F.; Champollion, C.; Chéry, J.; Doerflinger, E. Impact of high-resolution data assimilation of GPS zenith delay on Mediterranean heavy rainfall forecasting. Ann. Geophys. 2009, 27, 2739–2753. [Google Scholar] [CrossRef]
- Bender, M.; Dick, G.; Ge, M.; Deng, Z.; Wickert, J.; Kahle, H.-G.; Raabe, A.; Tetzlaff, G. Development of a GNSS water vapour tomography system using algebraic reconstruction techniques. Adv. Space Res. 2011, 47, 1704–1720. [Google Scholar] [CrossRef] [Green Version]
- Perler, D.; Geiger, A.; Hurter, F. 4D GPS water vapor tomography: New parameterized approaches. J. Geod. 2011, 85, 539–550. [Google Scholar] [CrossRef] [Green Version]
- Notarpietro, R.; Cucca, M.; Gabella, M.; Venuti, G.; Perona, G. Tomographic reconstruction of wet and total refractivity fields from GNSS receiver networks. Adv. Space Res. 2011, 47, 898–912. [Google Scholar] [CrossRef]
- Van Baelen, J.; Reverdy, M.; Tridon, F.; Labbouz, L.; Dick, G.; Bender, M.; Hagen, M. On the relationship between water vapour field evolution and the life cycle of precipitation systems. Q. J. R. Meteorol. Soc. 2011, 137, 204–223. [Google Scholar] [CrossRef] [Green Version]
- Brenot, H.; Walpersdorf, A.; Reverdy, M.; van Baelen, J.; Ducrocq, V.; Champollion, C.; Masson, F.; Doerflinger, E.; Collard, P.; Giroux, P. A GPS network for tropospheric tomography in the framework of the Mediterranean hydrometeorological observatory Cévennes-Vivarais (southeastern France). Atmos. Meas. Tech. 2014, 7, 553–578. [Google Scholar] [CrossRef] [Green Version]
- Brenot, H.; Champollion, C.; Deckmyn, A.; Van Malderen, R.; Kumps, N.; Warnant, R.; Mazière, M. Humidity 3D field comparisons between GNSS tomography, IASI satellite observations and ALARO model. Geophys. Res. Abst. 2012, 14, 2012–4285. [Google Scholar]
- Rohm, W.; Bosy, J. Local tomography troposphere model over mountains area. Atmos. Res. 2009, 93, 777–783. [Google Scholar] [CrossRef]
- Rohm, W.; Bosy, J. The verification of GNSS tropospheric tomography model in a mountainous area. Adv. Space Res. 2011, 47, 1721–1730. [Google Scholar] [CrossRef]
- Ducrocq, V.; Ricard, D.; Lafore, J.-P.; Orain, F. Storm-Scale Numerical Rainfall Prediction for Five Precipitating Events over France: On the Importance of the Initial Humidity Field. Weather Forecast. 2002, 17, 1236–1256. [Google Scholar] [CrossRef]
- Bender, M.; Stosius, R.; Zus, F.; Dick, G.; Wickert, J.; Raabe, A. GNSS water vapour tomography—Expected improvements by combining GPS, GLONASS and Galileo observations. Adv. Space Res. 2011, 47, 886–897. [Google Scholar] [CrossRef]
- Champollion, C.; Flamant, C.; Bock, O.; Masson, F.; Turner, D.D.; Weckwerth, T. Mesoscale GPS tomography applied to the 12 June 2002 convective initiation event of IHOP_2002. Q. J. R. Meteorol. Soc. 2009, 135, 645–662. [Google Scholar] [CrossRef]
- Rohm, W. The ground GNSS tomography-unconstrained approach. Adv. Space Res. 2013, 51, 501–513. [Google Scholar] [CrossRef]
- Rohm, W.; Zhang, K.; Bosy, J. Limited constraint, robust Kalman filtering for GNSS troposphere tomography. Atmos. Meas. Tech. 2014, 7, 1475–1486. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Q.; Yao, Y.; Yao, W. A troposphere tomography method considering the weighting of input information. Ann. Geophys. 2017, 35, 1327–1340. [Google Scholar] [CrossRef] [Green Version]
- Choy, S.; Zhang, K.; Wang, C.; Li, Y.; Kuleshov, Y. Remote Sensing of the Earth’s Lower Atmosphere during Severe Weather Events using GPS Technology: A Study in Victoria, Australia. In Proceedings of the 24th International Technical Meeting of The Satellite Division of the Institute of Navigation (ION GNSS 2011), Portland, OR, USA, 20–23 September 2011; pp. 559–571. [Google Scholar]
- Jenkins, M.; Lillebuen, S. Mini-Cyclone Melbourne Storm Causes Transport Sporting Event Chaos. 2010. Available online: https://www.smh.com.au/national/minicyclone-storm-lashes-melbourne-20100306-ppjb.html (accessed on 6 March 2010).
- Le Marshall, J.; Xiao, Y.; Norman, R.; Zhang, K.; Rea, A.; Cucurull, L.; Seecamp, R.; Steinle, P.; Puri, K.; Le, T. The beneficial impact of radio occultation observations on Australian Region forecasts. Aust. Meteorol. Oceanogr. J. 2010, 60, 121–125. [Google Scholar] [CrossRef] [Green Version]
- Lutz, R.; Loyola, D.; Gimeno García, S.; Romahn, F. OCRA radiometric cloud fractions for GOME-2 on MetOp-A/B. Atmos. Meas. Tech. 2016, 9, 2357–2379. [Google Scholar] [CrossRef] [Green Version]
- Vasilkov, A.; Joiner, J.; Spurr, R.; Bhartia, P.K.; Levelt, P.; Stephens, G. Evaluation of the OMI cloud pressures derived from rotational Raman scattering by comparisons with other satellite data and radiative transfer simulations. J. Geophys. Res. 2008, 113, D15S19. [Google Scholar] [CrossRef] [Green Version]
- Puri, K.; Dietachmayer, G.; Steinle, P.; Dix, M.; Rikus, L.; Logan, L.; Naughton, M.; Tingwell, C.; Xiao, Y.; Barras, V.; et al. Implementation of the initial ACCESS numerical weather prediction system. Aust. Meteorol. Oceanogr. J. 2013, 63, 265–284. [Google Scholar] [CrossRef]
- Manning, T.; Zhang, K.; Rohm, W.; Choy, S.; Hurter, F. Detecting severe weather using GPS tomography: An Australia case study. J. Glob. Position. Syst. 2012, 11, 58–70. [Google Scholar] [CrossRef]
- Askne, J.; Nordius, H. Estimation of tropospheric delay for microwaves from surface weather data. Radio Sci. 1987, 22, 379–386. [Google Scholar] [CrossRef]
- Dach, R.; Hugentobler, U.; Fridez, P.; Meindl, M. Bernese GPS Software Version 5.0. User Manual; Astronomical Institute, University of Bern: Bern, Switzerland, 2007. [Google Scholar]
- Rohm, W.; Yuan, Y.; Biadeglgne, B.; Zhang, K.; Marshall, J.L. Ground-based GNSS ZTD/IWV estimation system for numerical weather prediction in challenging weather conditions. Atmos. Res. 2014, 138, 414–426. [Google Scholar] [CrossRef]
- Boehm, J.; Niell, A.; Tregoning, P.; Schuh, H. Global Mapping Function (GMF): A new empirical mapping function based on numerical weather model data. Geophys. Res. Lett. 2006, 33, L07304. [Google Scholar] [CrossRef] [Green Version]
- Van Malderen, R.; Brenot, H.; Pottiaux, E.; Beirle, S.; Hermans, C.; De Mazière, M.; Wagner, T.; De Backer, H.; Bruyninx, C. A multi-site intercomparison of integrated water vapour observations for climate change analysis. Atmos. Meas. Tech. 2014, 7, 2487–2512. [Google Scholar] [CrossRef] [Green Version]
- Saastamoinen, J. Atmospheric Correction for the Troposphere and Stratosphere in Radio ranging of satellites. Geophys. Monogr. Ser. 1972, 15, 247–251. [Google Scholar]
- Brenot, H.; Ducrocq, V.; Walpersdorf, A.; Champollion, C.; Caumont, O. GPS zenith delay sensitivity evaluated from high-resolution numerical weather prediction simulations of the 8–9 September 2002 flash flood over southeastern France. J. Geophys. Res. 2006, 111, D15105. [Google Scholar] [CrossRef] [Green Version]
- Brenot, H.; Errera, Q.; Champollion, C.; Verhoelst, T.; Kumps, N.; Van Malderen, R.; Van Roozendael, M. Gnss tomography and and optimal geometrical setting to retrieve water vapour density of the neutral atmosphere. Geophys. Res. Abst. 2014, 16, U2014–U12204. [Google Scholar]
- Herring, T.A. Modeling Atmospheric Delays in the Analysis of Space Geodetic Data. In Proceedings of the Symposium on Refraction of Transatmospheric Signals in Geodesy, The Hague, The Netherlands, 19–22 May 1992; Geodetic, N., Ed.; Commission, Publications on Geodesy: Delft, The Netherlands, 1992. [Google Scholar]
- Chen, G.; Herring, T.A. Effects of atmospheric azimuthal asymmetry on the analysis of space geodetic data. J. Geophys. Res. Solid Earth 1997, 102, 20489–20502. [Google Scholar] [CrossRef]
- Elósegui, P.; Davis, J.L.; Gradinarsky, L.P.; Elgered, G.; Johansson, J.M.; Tahmoush, D.A.; Rius, A. Sensing atmospheric structure using small-scale space geodetic networks. Geophys. Res. Lett. 1999, 26, 2445–2448. [Google Scholar] [CrossRef] [Green Version]
- Ruffini, G.; Kruse, L.P.; Rius, A.; Bürki, B.; Cucurull, L.; Flores, A. Estimation of tropospheric zenith delay and gradients over the Madrid area using GPS and WVR data. Geophys. Res. Lett. 1999, 26, 447–450. [Google Scholar] [CrossRef] [Green Version]
- Manning, T. Sensing the Dynamics of Severe Weather Using 4D GPS Tomography in the Australian Region; School of Mathematical and Geospatial Sciences, RMIT University: Melbourne, Australia, 2013. [Google Scholar]
- Sargent, G.P. Computation of vapour pressure, dew-point and relative humidity from dry- and wet-bulb temperatures. Meteorol. Mag. 1980, 109, 238–246. [Google Scholar]
- Lawrence, M.G. The Relationship between Relative Humidity and the Dewpoint Temperature in Moist Air: A Simple Conversion and Applications. Bull. Am. Meteorol. Soc. 2005, 86, 225–234. [Google Scholar] [CrossRef]
- Sonntag, D. Advancements in the field of hygrometry. Meteorol. Z. 1994, 3, 51–66. [Google Scholar] [CrossRef]
- Davis, J.L.; Herring, T.A.; Shapiro, I.I.; Rogers, A.E.E.; Elgered, G. Geodesy by radio interferometry: Effects of atmospheric modeling errors on estimates of baseline length. Radio Sci. 1985, 20, 1593–1607. [Google Scholar] [CrossRef]
- Biondi, R.; Neubert, T.; Syndergaard, S.; Nielsen, J.K. Radio occultation bending angle anomalies during tropical cyclones. Atmos. Meas. Tech. 2011, 4, 1053–1060. [Google Scholar] [CrossRef] [Green Version]
- Pincus, R.; Beljaars, A.; Buehler, S.A.; Kirchengast, G.; Ladstaedter, F.; Whitaker, J.S. The Representation of Tropospheric Water Vapor Over Low-Latitude Oceans in (Re-)analysis: Errors, Impacts, and the Ability to Exploit Current and Prospective Observations. Surv. Geophys. 2017, 38, 1399–1423. [Google Scholar] [CrossRef]
- Kursinski, E.R.; Gebhardt, T. A Method to Deconvolve Errors in GPS RO-Derived Water Vapor Histograms. J. Atmos. Ocean. Technol. 2014, 31, 2606–2628. [Google Scholar] [CrossRef]
- Ladstädter, F.; Steiner, A.K.; Schwärz, M.; Kirchengast, G. Climate intercomparison of GPS radio occultation, RS90/92 radiosondes and GRUAN from 2002 to 2013. Atmos. Meas. Tech. 2015, 8, 1819–1834. [Google Scholar] [CrossRef] [Green Version]
- Bender, M.; Raabe, A. Preconditions to ground based GPS water vapour tomography. Ann. Geophys. 2007, 25, 1727–1734. [Google Scholar] [CrossRef]
- Möller, G. Reconstruction of 3D Wet Refractivity Fields in the Lower Atmosphere along Bended GNSS Signal Paths; SVH Südwestdeutscher Verlag für Hochschulschriften: Saarbrücken, Germany, 2017. [Google Scholar]
- Brenot, H.; Neméghaire, J.; Delobbe, L.; Clerbaux, N.; De Meutter, P.; Deckmyn, A.; Delcloo, A.; Frappez, L.; Van Roozendael, M. Preliminary signs of the initiation of deep convection by GNSS. Atmos. Chem. Phys. 2013, 13, 5425–5449. [Google Scholar] [CrossRef] [Green Version]
- Hogg, D.-C.; Guiraud, F.-O.; Decker, M.-T. Measurement of excess radio transmission length on earth-space paths. Astron. Astrophys. 1981, 95, 304–307. [Google Scholar]
- Niell, A.E. Global mapping functions for the atmosphere delay at radio wavelengths. J. Geophys. Res. Solid Earth 1996, 101, 3227–3246. [Google Scholar] [CrossRef]
- Bevis, M.; Businger, S.; Chiswell, S.; Herring, T.A.; Anthes, R.A.; Rocken, C.; Ware, R.H. GPS Meteorology: Mapping Zenith Wet Delays onto Precipitable Water. J. Appl. Meteorol. 1994, 33, 379–386. [Google Scholar] [CrossRef]
- Vedel, H.; Mogensen, K.S.; Huang, X.-Y. Calculation of zenith delays from meteorological data comparison of NWP model, radiosonde and GPS delays. Phys. Chem. Earth Part A Solid Earth Geod. 2001, 26, 497–502. [Google Scholar] [CrossRef]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Zus, F.; Bender, M.; Deng, Z.; Dick, G.; Heise, S.; Shang-Guan, M.; Wickert, J. A methodology to compute GPS slant total delays in a numerical weather model. Radio Sci. 2012, 47, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Möller, G.; Landskron, D. Atmospheric bending effects in GNSS tomography. Atmos. Meas. Tech. 2019, 12, 23–34. [Google Scholar] [CrossRef] [Green Version]
- Tarantola, A. Inverse Problem Theory and Methods for Model Parameter Estimation; SIAM (Society of Industrial and Applied Mathematics): Philadelphia, PA, USA, 2005. [Google Scholar]
- Zelinka, I.; Skanderova, L. Simulated Annealing in Research and Applications, Simulated Annealing—Single and Multiple Objective Problems; InTech: Vienna, Austria, 2012; ISBN 978-953-51-0767-5. [Google Scholar]
- Onwubolu, G.; Babu, B. V New Optimization Techniques in Engineering; Springer: Berlin/Heidelberg, Germany, 2004; ISBN 3-540-20167X. [Google Scholar]
- Kačmařík, M.; Rapant, L. New GNSS tomography of the atmosphere method—Proposal and testing. Geoinform. FCE CTU 2012, 9, 63–76. [Google Scholar] [CrossRef] [Green Version]
- Censor, Y.; Elfving, T. Block-Iterative Algorithms with Diagonally Scaled Oblique Projections for the Linear Feasibility Problem. SIAM J. Matrix Anal. Appl. 2002, 24, 40–58. [Google Scholar] [CrossRef] [Green Version]
- Jiang, M.; Wang, G. Convergence of the simultaneous algebraic reconstruction technique (SART). IEEE Trans. Image Process. 2003, 12, 957–961. [Google Scholar] [CrossRef]
- Jiang, M.; Wang, G. Convergence studies on iterative algorithms for image reconstruction. IEEE Trans. Med. Imaging 2003, 22, 569–579. [Google Scholar] [CrossRef] [PubMed]
- Censor, Y.; Elfving, T.; Herman, G.T.; Nikazad, T. On Diagonally Relaxed Orthogonal Projection Methods. SIAM J. Sci. Comput. 2008, 30, 473–504. [Google Scholar] [CrossRef] [Green Version]
- Qu, G.; Wang, C.; Jiang, M. Necessary and Sufficient Convergence Conditions for Algebraic Image Reconstruction Algorithms. IEEE Trans. Image Process. 2009, 18, 435–440. [Google Scholar] [PubMed]
















| Mean Times of Measurement | Cosmic-GPS Couple | Lower Position | Top of Tomography Grid | Higher Position |
|---|---|---|---|---|
| 3 March, 2010 08:07 UTC | C006-G09 | (37.99°S, 145.98°E, 2300 m) | (37.71°S, 145.17°E, 12,800 m) | (37.66°S, 144.62°E, 39,900 m) |
| 4 March, 2010 16:39 UTC | C004-G12 | (37.33°S, 147.03°E, 1900 m) | (38.81°S, 146.21°E, 12,800 m) | (37.66°S, 144.62°E, 39,900 m) |
| 8 March, 2010 05:36 UTC | C003-G01 | (37.04°S, 142.60°E, 1200 m) | (38.25°S, 142.33°E, 12,800 m) | (38.86°S, 142.35°E, 39,900 m) |
| 8 March, 2010 07:33 UTC | C006-G27 | (36.83°S, 144.63°E, 1300 m) | (36.41°S, 143.26°E, 12,800 m) | (36.32°S, 142.52°E, 39,900 m) |
| Tomography Model | Inversion | Dim. | Retrievals | Covariance Operator Data | Covariance Operator A Priori Model | Quality Check |
|---|---|---|---|---|---|---|
| BIRA | SVD, weighted and damped LS adjustment | 3D | , | 10% | 90% | Resolution matrix, covariance matrix, spread |
| WUELS | Kalman filter with selective SVD | 3D | , | Diagonal obs. error fed | Diagonal-height-dependent | Condition number and variance–covariance , |
| TUW | TSVD | 3D | Elevation dependent weighting | Altitude-dependent weights | RMS of weighted residuals | |
| UBI | SART | 3D | Unit covariance matrix | Unit covariance matrix | Condition number and converge | |
| TUO | LS adjustment | 2D | , | - | - | - |
| Parameter | Value | Unit | Absolute Uncertainty | Relative Error |
| Rd | 287.0586 | J/(kmol K) | ±0.0055 | ±0.002% |
| Rw | 461.525 | J/(kmol K) | ±0.013 | ±0.003% |
| k1 | 77.60 | K/hPa | ±0.05 | ±0.064% |
| k2 | 70.4 | K/hPa | ±2.2 | ±3.125% |
| k3 | 373900 | K2/hPa | ±1200 | ±0.321% |
| k2’ | 22.1345 | K/hPa | ±2.2352 | ±10.090% |
| Parameter | Typical Value | Unit | Absolute Uncertainty | Relative Error |
| PS | 1000 | hPa | ±2 (±1) | ±0.200% (±0.100%) |
| Tm | 285 | K | ± 1 (±0.5) | ±0.351% (±0.175%) |
| gm | 9.807 | m.s−2 | ±0.022 | ±0.227% |
| ZTD | 2.54 | m | ± Formal error + 0.010 (+ 0.005) | ±0.497% (±0.296%) |
| ZHD | 2.29 | m | ±0.011 (±0.007) | ±0.494% (±0.326%) |
| ZWD | 0.25 | m | ±0.019 (±0.010) | ±8.605% (±4.503%) |
| κ | 159 | kg/m3 | ±1.335 (±1.053) | ±0.840% (±0.622%) |
| IWV | 40 | kg/m2 | ±3.375 (±2.513) | ±8.440% (±6.260%) |
| Variable *, mean: 0.765 | m | Variable *, mean: ±0.069 | Mean: ±9.020% | |
and (GEW, GNS) | Variable *, mean: 0.027 [GEW, GNS] = [5, 5] | m (mm, mm) | Variable *, mean: ±0.003 (±0.001) ± Formal error + [0.8, 0.6] ([0.4, 0.2]) | Mean: ±10.249% (±5.137%) |
| SWD | Variable *, mean: 0.792 | m | Variable *, mean: ±0.072 (±0.039) | Mean: ±9.091% (±4.924%) |
| SIWV | Variable *, mean: 122 | kg/m2 | Variable *, mean: ±12.230 (±6.238) | Mean: ±10.003% (±5.098%) |
| Data Type | Initial Observations (IO) | IO with Additional Pseudo-Observations | Observations Modified Considering Uncertainties | |||||
|---|---|---|---|---|---|---|---|---|
| Positive | Negative | Positive | Negative | |||||
 | Every 6 h | First Epoch Only | Every 6 h | First Epoch Only | Every 6 h | First Epoch Only | ||
| No | Tests a and A | Tests b and B | Test Aπ | Test Bπ | Tests A+, A(+) | Tests A−, A(−) | Tests B+, B(+) | Tests B−, B(−) |
| 30 min | Test A30 | Test B30 | Test Aπ30 | Test Bπ30 | Tests A30+, A30(+) | Tests A30-, A30(−) | Tests B30+, B30(+) | Tests B30-, B30(−) |
| 60 min | Test A60 | Test B60 | - | - | Tests A30+, A30(+) | Tests A30-, A30(−) | Tests B30+, B30(+) | Tests B30-, B30(−) |
| 120 min | Test A120 | Test B120 | - | - | Tests A120+, A120(+) | Tests A120-, A120(−) | Tests B120+, B120(+) | Tests B120-, B120(−) |
| Type of Tomography Calculation | No Stacking | Stacked Data (30 min) | Stacked Data (60 min) | Stacked Data (120 min) | Pseudo-Slant Observations | ||
|---|---|---|---|---|---|---|---|
| No Stacking | Stacked Data (30 min) | ||||||
| Mean Number of SLANTGPS | 685 | 1370 | 2050 | 3400 | 3140 | 6275 | |
| Geometrical Distribution (% of Voxels Crossed) for Different Layers | 0–1 km | 51.2 | 51.2 | 51.2 | 51.4 | 82.9 | 84.6 |
| 1–2 km | 58.3 | 58.3 | 58.3 | 61.6 | 88.0 | 89.4 | |
| 2–4 km | 65.6 | 66.0 | 67.4 | 72.2 | 93.1 | 93.1 | |
| 4–6 km | 73.6 | 75.0 | 76.4 | 82.6 | 95.8 | 97.2 | |
| 6–9 km | 77.0 | 81.3 | 84.0 | 87.5 | 92.4 | 93.1 | |
| 9–13 km | 61.8 | 67.4 | 67.8 | 70.6 | 64.6 | 68.0 | |
| All | 67.8 | 69.3 | 69.5 | 72.0 | 92.8 | 93.7 | |
| Indicator of Mean Time of Processing (minutes) | 0.5 | 1 | 2 | 8 | 7 | 130 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brenot, H.; Rohm, W.; Kačmařík, M.; Möller, G.; Sá, A.; Tondaś, D.; Rapant, L.; Biondi, R.; Manning, T.; Champollion, C. Cross-Comparison and Methodological Improvement in GPS Tomography. Remote Sens. 2020, 12, 30. https://doi.org/10.3390/rs12010030
Brenot H, Rohm W, Kačmařík M, Möller G, Sá A, Tondaś D, Rapant L, Biondi R, Manning T, Champollion C. Cross-Comparison and Methodological Improvement in GPS Tomography. Remote Sensing. 2020; 12(1):30. https://doi.org/10.3390/rs12010030
Chicago/Turabian StyleBrenot, Hugues, Witold Rohm, Michal Kačmařík, Gregor Möller, André Sá, Damian Tondaś, Lukas Rapant, Riccardo Biondi, Toby Manning, and Cédric Champollion. 2020. "Cross-Comparison and Methodological Improvement in GPS Tomography" Remote Sensing 12, no. 1: 30. https://doi.org/10.3390/rs12010030
APA StyleBrenot, H., Rohm, W., Kačmařík, M., Möller, G., Sá, A., Tondaś, D., Rapant, L., Biondi, R., Manning, T., & Champollion, C. (2020). Cross-Comparison and Methodological Improvement in GPS Tomography. Remote Sensing, 12(1), 30. https://doi.org/10.3390/rs12010030