1. Introduction
Mapping Earth’s surface and its rapid changes with remotely sensed data are a crucial task to help understand the impact of an increasingly urban world population on the environment. The information provided by urban scene classification and change maps are quite important for urban planners, environmental engineers, and decision makers in general. Land Use/Land Cover (LULC) classes are established categorical variables that represent the status of the Earth’s surface in a viable way. In the last couple decades, several studies have investigated the classification of urban scenes using remote sensing data. Remotely sensed data provides cheap, comprehensive, and easy to use source to map the location and the spatial extent of different LULC classes. With its rich information content, multispectral optical images have been used intensively for urban scene classification [
1,
2,
3,
4,
5,
6]. Unlike optical, radar images have lower spectral information content. Nevertheless, these images are not affected by atmospheric and solar illumination conditions. Several studies have shown the potential of these images in urban classification [
7,
8,
9,
10,
11,
12,
13]. The successful use of remote sensing data for urban scene classification depends on several considerations (e.g., image spatial resolution, acquisition time, spectral information, classification scheme, etc.). Another factor of crucial importance and that has strong impact on the classification accuracy, in general, is the input features and their quality. It is quite common to use the raw input spectral images (e.g., green, red, NIR, radar cross section, etc.), or/and product derived from these spectral bands (e.g., NDBI, NDVI, NDWI) as input features. Texture measures (e.g., GLCM texture) have also played important role in increasing the discrimination between different LULC classes [
14,
15]. Features that can be used for scene classification are not restricted to raw image spectral bands or products derived from them. Several studies have shown that combining features extracted from images acquired at different times could help significantly improving the classification accuracy [
11,
16,
17,
18,
19]. The basic idea is that despite the fact that some LULC classes would look very similar in one season/time, they tend to look quite different in another. By combining images acquired in different times, therefore, it is possible increase classes’ separability.
Because of their different modalities, optical and SAR provide quite different information about earth surface. The response of earth surface materials to the short wavelength energy used by optical sensors depends to a high extent on the biochemical properties of the observed objects. Conversely, radar response is often associated with other factors such as objects geometrical properties (e.g., roughness), and its moisture content. It is therefore natural to think of SAR and optical images as complementary to each other [
20]. Several studies have investigated the possibility to improve classification accuracy through the fusion of SAR and optical images [
21,
22,
23]. Fusion can be carried out at the feature, pixel, or information level. The former approach consists of combining features extracted from different data sources into a one augmented feature vector; it can then be an input of any classification algorithm. Because of the simplicity involved, this approach has been the focus of several studies [
24,
25,
26,
27,
28]. In fact, the multitemporal image classification approach discussed in the previous section can be envisaged as a feature-level fusion technique; this approach was further extended by the fusion of multitemporal and multi-source features extracted from Radarsat-2 and QuickBird images for urban land-cover mapping [
29]. Despite the availability of a large selection of features that can be used for the classification task, most studies only consider a few of them. This could be attributed to the fact that in many cases features will be highly correlated, i.e., they contain redundant information. Including such features would serve nothing other than slowing down the classification process. Another reason is that features computation (e.g., GLCM textures) is time consuming and handling large dataset with many features is not easy in common image classification software [
30]. For this reason, the analyst faces the problem of selecting few out of hundredth of available features (e.g., spectral band, GLCM textures, and indices). Usually, expert knowledge is used to manually select a few, allegedly promising features, even though numerous algorithms exist that could perform the dimensionality reduction task automatically [
31,
32,
33,
34,
35,
36].
Dimensionality reduction is the process of simplifying the classification task by either transforming the original features to a representation in a set of lower dimensionality (feature extraction) or by removing redundant and irrelevant features (feature selection) [
37]. A well-known feature extraction method is principal component analysis (PCA) [
38]. It projects the input feature space to a new space in which feature will be uncorrelated. It also compresses (i.e., dimensionality reduction) the information into few output features that contain most of the information available in the original space. Unlike PCA, linear discriminant analysis (LDA) is a supervised feature extraction method that projects the input feature space in a way that maximizes the separation between the classes [
39]. With large representative training data, LDA is expected to outperform PCA since it takes samples classes into consideration [
40]. Feature selection methods can be grouped into three main categories: filters, wrappers, and embedded methods [
37,
41]. While filters rank features according to some predefined statistic and remove lowest ranking features, wrappers utilize learning machines to find the best performing subset of features. Embedded methods find optimal feature subsets during training and are integral parts of certain learning machines. In particular, filters are independent of the learning machine and they evaluate feature importance based on data characteristics [
42]. Univariate filters compute a feature’s quality individually, assuming independence between the features, while multivariate filters take possible dependencies into account and perform assessment in batches.
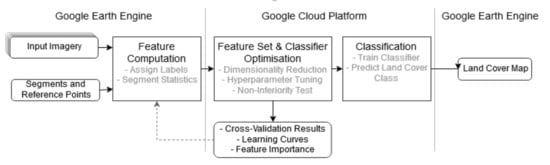
The frequent acquisition of satellite imagery leads to an impressive amount of data that is collected and published on a daily basis. An efficient means of access and an infrastructure that allows large-scale processing of this big EO data are needed to fully exploit it. Google Earth Engine (GEE) is a cloud-based platform for planetary-scale geospatial analysis that utilizes the massive computational capabilities of Google’s servers. It facilitates access to geographical and remote sensing data in their “multi-petabyte analysis-ready data catalog” [
43]. GEE allows for effective processing through subdivision and distribution of computations. In general, GEE lowers the threshold for large-scale geospatial computation and makes it possible “for everyone” [
43]. Though, GEE offers valuable opportunities for EO data analysis it could be vastly enhanced with an integration with Google Cloud Platform (GCP) (
https://cloud.google.com/). GCP provides Google Compute Engine, which offers scalable and customizable virtual machines for cloud computing and Google Cloud Storage, a service for storing and accessing data. It allows different types of storage based on the desired access-frequency and the intended use. On GCP, external libraries can be used for further processing and deeper analysis of data derived from GEE. One example is Scikit-learn, an open-source machine learning Python module [
44]. It contains a variety of machine learning models for classification, regression, and clustering [
45]. Besides implementations of machine learning models, it contains tools for model selection, cross-validation, hyperparameter tuning, and model evaluation as well as dimensionality reduction, feature decomposition, and feature selection.
In this study, we will utilize the computational power of Google Earth Engine (GEE) and Google Cloud Platform (GCP) to generate an oversized feature set extracted form Sentinel1 and Sentinel2 multitemporal images. We will explore feature importance and analyze the potential of different dimensionality reduction methods. A large feature set is evaluated to find the most relevant features which discriminate the classes well and thereby contribute most to achieve high classification accuracy. In doing so, we present an automated alternative to the sensitive knowledge-based but tedious and sometimes biased selection of input features. Three methods of dimensionality reduction, i.e., linear discriminant analysis (LDA), mutual information-based (MI), and Fisher-criterion-based (F-Score), will be tested and evaluated. LDA is a feature extraction method that transform the original feature space into a projected space of lower dimensionality. MI and F-score belong to the group of filter-based univariate feature selection methods that rank and filter the features according to some statistic. We evaluate the optimized feature sets against an untreated feature set in terms of classification accuracy, training and prediction performance, data compression, and sensitivity to training set sizes.
For features classification, a support vector machine (SVM) is chosen. SVM is a supervised non-parametric machine learning algorithm [
46]. Although it is commonly used for classification tasks, it has also been used for regression. SVM maps the input features space to a higher dimensional space using kernel functions (e.g., radial basis function). The training samples are separated in the new space by a hyperplane (defined by the support vectors) that guarantee the largest margin between the classes. It has been used successfully in different types of remote sensing applications—for example, classification [
47,
48,
49], change detection [
50,
51,
52], and in image fusion [
53]. Depending on the size of the training sample, SVM is known for being slow during the training phase. However, the classification phase is quite fast since it only depends on a few training samples known as the support vector. The spatial resolutions of Sentinel-1 (S1) SAR data and Sentinel-2 (S2) MSI sensors are moderate (e.g., 10 m) and the classification will often use the pixel-based approach. Geographic object-based image analysis (GEOBIA) is often applied when using high spatial resolution data [
54,
55]. However, given the large extent of the study areas, which surpasses even the largest case studies compared in a recent review of object-based methods by a factor of a thousand [
56], we adopted an object-based classification even though the analysis will be based on S1 and S2 images. The application of GEOBIA to moderate spatial resolution is not very common, however is not rare either [
57]. The object-based paradigm allows us to reduce the computational complexity immensely, and consequently, allow us to put more emphasis on the main goal of this paper, which is the investigation of feature selection for urban scenes classification.
In summary, we provide a framework that derives features from GEE’s data catalogue. We deliver a prototype for GCP that applies dimensionality reduction and feature set optimization methods and tunes the classifier’s hyperparameters in an exhaustive search. Performances on the different feature sets are compared to each other with statistical measures, different visualization methods, and a non-inferiority test for the highest dimensionality reduction satisfying the chosen performance requirements. The overall aim is the exploration of feature importance in the big EO data that are available today. Understanding the feature importance leads to an improved classification accuracy by the removal of irrelevant features and to an increased classification throughput by the reduction of the datasets. We demonstrate the applicability of our methodology in two different study sites (i.e., Stockholm and Beijing) based on a multitemporal stack of S1 and S2 imagery. For the given classification scheme, we find the best feature set that achieve the highest overall accuracy. A further analysis of the feature selection allows us to evaluate the importance of individual features to the classification task.
2. Study Areas and Data Description
We demonstrate our methodology on two study areas. One is based on a scheme of 10 LULC classes in the urban area of Stockholm, while the other is based on 8 LULC classes scheme in the urban area of Beijing. The study areas are shown in (
Figure 1) and cover 450,000 ha in Stockholm and 518,000 ha in Beijing. The classes represent the dominant land cover and land use types in the respective areas as demonstrated in [
58,
59], and are derived from urban planning applications and urban sprawl monitoring. The classification schemas adopted for the study areas were defined in previous projects [
58,
59] to monitor the urbanization process and evaluate the corresponding environmental impact;
Table 1 provides an overview of the selected classes. We used reference points that were manually collected by remote sensing experts not involved in this study [
58,
59] and we divided them in training and validation sets. In Stockholm, these reference points are approximately uniformly distributed over most classes (≈1000 samples per class, except 500 for bare rock and wetlands). In Beijing, there are in general fewer reference points with more imbalanced classes (70 samples for urban green space up to 175 for forests).
As mentioned earlier, an object-based approach has been adopted in order to reduce the computational burden and focus more on the feature selection and classification. The segmented image-objects should aim to depict the entities of the urban land cover types. For the detection of low-density built-up areas, which are a dense mix of built-up and vegetated pixels, an object-based approach is beneficial. Additionally, the separation of high-density built-up areas and roads can benefit from the geometric properties of the objects (e.g., minimum enclosing circle, minimal area rotated rectangle, and least-squared fitted ellipse).
For both study areas, the segmentation is performed using a multiresolution module of eCognition software [
60]. The segmentation is based on the S2 10 m spectral bands. The segments are created using a scale parameter of 50, a shape vs. color ratio of 0.7:0.3 and a compactness vs. smoothness ratio of 0.7:0.3. The parameters were selected based on repeated tests for a subjectively good segmentation (compare
Figure 2,
Figure 3 and
Figure 4). The criteria of this selection were mainly the proper distinction of segments containing LDB (low density built-up) in comparison to UGS (urban green spaces); and R (roads and railroads) in comparison to HDB (high density built-up). The adequacy of a segmentation layout can only be assessed in the context of an application. Consequently, the traditional approach has been to use human expert to evaluate the quality of the segmentation [
59]. However, when facing big EO data, the segmentation process and determination of its parameters needs to be automated. Several approaches have been proposed [
61,
62,
63] and should be evaluated for efficient integration in the workflow.
Using the reference data, the segments were labeled based on the class of the reference point located in the segment. Inside Stockholm lies a total of 5800 labeled segments and an additional 200,000 unlabeled segments (~3% labeled). In Beijing 1100 segments are labeled and 458,000 segments are unlabeled (~0.25% labeled). For Stockholm and Beijing, the analysis considers S1 and S2 images from the summer of 2015 and 2016, respectively (
Table 2). For S1 images, two orbit directions (i.e., ascending and descending) with two polarizations (i.e., VV and VH) are used and treated as individual inputs. Four temporal stacks are created (one for each direction/polarization). Each temporal stack is reduced by computing its temporal mean and standard deviation. This way, the speckle noise is reduced while still capturing temporal variations of the different LULC classes. For each mean and standard deviation image, 17 GLCM texture measures (
Table 3) estimated with kernel size of 9 × 9 are computed. Finally, for each segment, the mean, standard deviation, max, and min of the abovementioned features are computed (see
Table 4).
The S2 stack is filtered such that only images with less than 15% cloud cover is included. All S2 spectral bands were resampled to 10 m spatial resolution. In addition to the 12 spectral bands, normalized difference-vegetation and water indices (NDVI, and NDWI) are computed and added to the S2 stack. Additionally, 17 GLCM texture measures are computed for NIR (10 m) spectral band: we could have computed GLCM textures for all S2 spectral band but this would have increased the number of features tremendously (extra 748 features) without adding substantial new information considering the high correlation of texture between the available S2 bands. Moreover, since several S1 textures have been included, choosing only NIR texture will be enough for the objective of this paper. For each segment, four statistics (i.e., mean, standard deviation, min, and max) are computed for all the available images. Finally, 12 features describing the segments’ geometric properties are computed (see
Table 4 for details). In total, 712 features are computed in the GEE platform and exported into GCP (see
Table 4).
5. Conclusions
This study demonstrates the feasibility of GEE and GCP infrastructure to apply dimensionality reduction through feature extraction and feature selection methods for object-based land cover classifications with oversized feature sets. The presented workflow allows thorough assessments of different features as well as different dimensionality reduction methods for specific GEOBIA applications. It incorporates the dimensionality reduction as a key step in the land cover classification process, which we consider essential for the exploitation of the growing EO big data.
The LDA showed the highest compression of the initial feature space and can obtain remarkable results in comparison to the default SVM. One disadvantage, however, is that this method gives no intuitive indication about the contribution of individual features to the accuracy and is less reliable with small training sets. The feature selection methods appear very promising and provide exactly this insight into the features’ quality. With a sensitive non-inferiority margin, both MI and F-Score allowed high compressions of the feature set and achieved notable improvements of the accuracy. This emphasizes the fact that dimensionality reduction should form a key step in land cover classification using SVM. Thanks to the availability of cloud computing, these dimensionality reduction processes are no longer limited by the lack of computational power and can easily be integrated into the classification workflow.
Despite the different training set sizes in the two study areas, the averaged feature importance ranking showed similar results for the top-ranking features. It strongly indicates that a feature-level fusion of SAR data from Sentinel-1 and multispectral imagery from Sentinel-2 allows for a better discrimination between different LULC classes. It should be acknowledged, however, that the optimal set of features is specific for each classification scheme. Different land cover classes require different features to be separable from one another. Future research should therefore expand this method to different classification schemes but also further investigate the importance of features for each individual class. To explore the relevance of features for a land cover classification more broadly, additional features need to be included in the analysis. More spectral indices should be included; thorough multi-temporal analyses of optical or SAR imagery are promising candidates to improve land cover; analysis of the phenology through harmonic or linear fitting of the NDVI, for example, help to distinguish between different vegetation classes.
Despite their limitation, LDA, MI, and F-Score serve as a demonstration of the integration in the workflow. In future work, different feature selection methods should be tested following the proposed methodology. Multivariate filter methods, in particular, should be explored, since the applied univariate methods fail to identify the dependency between similar high-ranked features. Moreover, wrappers and embedded methods especially designed for the chosen classifier should be included in the analysis as well.
Considering the multiple types of sensors and the massive amount of data that is already available and that will be available in the next years, we think that the developed framework can be used to analyze the importance of the different input data and the derived features; it can contribute to understanding how to optimize the integration of these different data sources (i.e., very high-resolution SAR and multispectral data) for object-based classification analysis.
The Python scripts developed during this study are released in a public GitHub repository and licensed under GNU GPL v3.0 [
71]. Additionally, the respective JavaScript snippets for the Google Earth Engine web API as well as the segmented image-objects and reference points are published and referenced in the GitHub repository. We hope that this might encourage further research and the development of reliable workflows for the efficient exploitation of today’s EO big data with inter-comparable results.