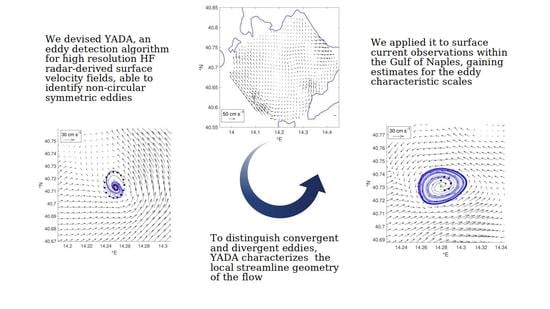
Eddy Detection in HF Radar-Derived Surface Currents in the Gulf of Naples

Abstract

Submesoscale eddies play an important role in the energy transfer from the mesoscale down to the dissipative range, as well as in tracer transport. They carry inorganic matter, nutrients and biomass; in addition, they may act as pollutant conveyors. However, synoptic observations of these features need high resolution sampling, in both time and space, making their identification challenging. Therefore, HF coastal radar were and are successfully used to accurately identify, track and describe them. In this paper we tested two already existing algorithms for the automated detection of submesoscale eddies. We applied these algorithms to HF radar velocity fields measured by a network of three radar systems operating in the Gulf of Naples. Both methods showed shortcomings, due to the high non-geostrophy of the observed currents. For this reason we developed a third, novel algorithm that proved to be able to detect highly asymmetrical eddies, often not properly identified by the previous ones. We used the results of the application of this algorithm to estimate the eddy boundary profiles and the eddy spatial distribution.

1. Introduction

Transport in the ocean develops over an extremely wide range of scales, from the basin to the dissipation scale (e.g., [1]). Our ability to observe and/or to model processes at smaller and smaller scales has greatly increased over the last few decades. Phenomena that in the very recent past could not be detected or described, and thus needed to be parametrized in terms of larger scales (e.g., [2,3]), are now subjects of consolidated research, as is the case of mesoscale features. Now, our focus has shifted to smaller dynamics, such as submesoscale motions. In the wide range of turbulent processes in the ocean, submesoscale eddies are the most volatile ones, due to their short lifetime (few hours) and length scale (below 10 km).

Submesoscale eddies principally act as energy conveyors from the mesoscale to the microscale, and play a crucial ecological role: they may influence the state of health of ocean regions through their ability to carry heat, inorganic matter, nutrients and biomass ([4,5]), ensuring the connectivity between different ecosystems ([6]). They are particularly important for phytoplankton, as they develop over timescales similar to those of phytoplankton growth ([7]), moreover, they may act as carriers of pollutants (see, e.g., [8]). Consequently the detection of eddies, behind its inherent interest, is crucial also for environmental applications.

As more and more synoptic, high resolution data on mesoscale and submesoscale eddies has become available, thanks to remote sensing techniques at different resolutions, automatic eddy detection methods have gained importance and interest. In the recent past, several eddy detection algorithms ([9,10,11,12,13]) have been developed and applied to velocity fields derived from altimeter data, numerical model outputs and HF radar observations. They can be divided into three families: geometrical, dynamical and hybrid ones. The definition depends on the flow characteristics extrapolated by the algorithm itself, that can be geometrical, dynamical or both (e.g., [9,10,11] and respectively). However, the existing methods have been mainly conceived for meso and larger scale recirculations, which display different kinematic characteristics than submesoscale eddies, in particular in terms of divergence and (a)symmetry of the flow field.

Mesoscale eddies scale with the first internal Rossby radius ([14,15]), which is of the order of 10 km in the Mediterranean (5 to 12 km according to [16]) and four to ten times as large in the north Atlantic ([17]). Differently, submesoscale surface eddies have characteristic lengths starting from $0.1$ km up to the mesoscale ([8,18]). They are completely confined in the surface mixed layer, within depths going from tens to hundreds of meters. Therefore, since their relative Rossby and Froude numbers, $\mathrm{Ro}$ and $\mathrm{Fr}$, are not small, these structures show highly non-geostrophic behavior, high divergent flow patterns and strong asymmetries. As a consequence, the aforementioned algorithms, typically designed to capture the features of vortices in geostrophic balance, may fail in detecting submesoscale eddies as they are often unable to characterize highly deformed, divergent or convergent motions. For this reason, we have designed a novel algorithm, presented in this paper, that has proved to be able to capture the noncircular symmetry and the divergent character of submesoscale recirculations.

High resolution data is needed in order to identify submesoscale motions. In this framework, HF radars are proving to be an almost irreplaceable tool: They are land-based remote sensing instruments which allow to observe surface currents at very high spatial and temporal resolution, thus suitable to monitor such small scale phenomena ([19,20]). Other remote sensing techniques are available, even with much higher spatial resolution, and are thus able to detect submesoscale flow features ([21,22,23], but they have very long revisit periods with respect to the hourly sampling provided by coastal radars, thus allowing for detecting but not for tracking such features.

In this study we have utilized HF radar observations of surface currents in the Gulf of Naples (GoN), a semi-enclosed area of the Tyrrhenian, a sub-basin of the western Mediterranean Sea. The GoN is surrounded by a coast characterized by a quite uneven orography, dominated by the presence of the Vesuvius volcano and of Mount Faito in the East, both exceeding 1000 m altitude, and of a number of lower hills very close to the northern coastline. It has a complex bathymetry, with an average depth of 170 m which reaches down to more than 800 m in correspondence of two major canyons, the Magnaghi and the Dohrn, which carve the shelf across the threshold connecting the Gulf with the open Tyrrhenian Sea. Its surface circulation is mainly wind driven, with a strong seasonal regime ([24,25]), even though the offshore circulation of the Southern Tyrrhenian may occasionally affect the current pattern in the interior of the GoN ([25] and references therein). The Gulf represents a very complex system: It hosts a heavily anthropized coastline, with industrial settlements in the immediate vicinity of the coast, side by side with four marine/natural protected areas. Moreover, oligotrophic and eutrophic characteristics coexist in the Gulf. Its outer portion is dominated by Tyrrhenian, oligotrophic waters, while the coastal part is typically eutrophic, as can be expected ([26,27]). Water exchange inside the Gulf is ruled by mechanisms acting at different spatial and temporal scales, triggered by external (local and remote) driving as well as by bottom topography and coastal constraints ([25,28,29,30,31]). Fixed-point long term investigations of the local plankton community composition have shown a strong variability of species, alternatively coming from the coast or from offshore ([32]). Recent investigations have pointed out the different roles of physical transport and biological processes, demonstrating in particular the effect of transient current patterns (e.g., [33]). For the above reasons we believe that the Gulf may well represent a universal example of a coastal area facing and intensively interacting with the open sea, but more importantly characterized by the coexistence of different subsystems. In such a framework, submesoscale eddies may act as an extremely powerful exchange mechanism among those subsystems for water and its biogeochemical content, and are therefore worthy of the maximum consideration.

The article is structured as follows. In Section 2 we describe our dataset and the dynamical fields that allow us to identify recirculating structures. Then in Section 3 we accurately describe the chosen detection algorithms, and in Section 4 we describe the algorithm tuning procedure and we provide a method for estimating eddy boundaries and radii. In Section 5 we discuss the results obtained by two algorithms and we analyze the spatial distribution of the detected eddies. Finally, in Section 6, we summarize our results and highlight some possible research directions.

2. Materials

2.1. Dataset

For this study we used the HF radar observations of surface currents in the GoN collected by a CODAR (Coastal Ocean Dynamics Application Radar) SeaSonde system. The product consists of a two-dimensional velocity field with a spatial resolution of 1 km over an area of approximately 20–30 km alongshore by 15–20 km offshore, and with an hourly frequency. The specifics of the radar network operating in the GoN can be found in [30]; see [20] for a review on HF radar theory and its applications to coastal current observations; [34] for a recent utilization of HF radar-detected transport to fisheries. Specific applications to the GoN in terms of description of the dynamics, data validation, as well as their use in conjunction with numerical models, can be found in [24,25,33,35,36,37,38]. The data utilized in this study refers to the late fall period 24 November through 8 December 2008. Since the number of eddies was clearly detectable in radar observations, we selected this period among many others, as a sort of training dataset for our algorithm, necessarily limited to a relatively short timespan for validation issues.

Since the observed GoN eddies have radii in a range between 0.5 and 5 km (we found a mean equivalent radius of approximately $0.8$ km, with extrema reaching 4 km) we decided (following [10]) to refine the grid to approximately 0.5 km, by means of a cubic interpolation, as illustrated in Figure 1.

With a reference velocity scale U of $10\mathrm{cm}{\mathrm{s}}^{-1}$, a length scale L of $1\mathrm{km}$ and a Coriolis parameter $f\sim 9.5·{10}^{-5}{\mathrm{s}}^{-1}$, the Rossby number is $\mathrm{Ro}\sim 1$. It is thus evident that the quasi-geostrophic equations are not accurate for describing the GoN dynamics.

2.2. Dynamical Parameters Characterizing Recirculations

At a first glance, eddies of two-dimensional turbulent flows can be described as flow regions characterized by a rigid-body rotation. In this approximation, many local and semi-local parameters can be adopted to decide whether vortices exist or are likely to develop. As eddies are extensive structures, it is natural to consider integral quantities, rather than pointwise ones, to identify them. Nevertheless, the choice of the appropriate computational regions, specifically their shape and area, is completely arbitrary. For this reason these parameters naturally depend on a scale coefficient.

2.2.1. Okubo–Weiss and Local Okubo–Weiss Parameters

The Okubo–Weiss parameter ($\mathrm{OW}$) is a local dynamical field which, loosely speaking, measures the relative dominance of the rate-of-strain tensor s over the vorticity $\omega$ of the velocity field (here $|.|$ denotes the euclidean module)

$$\mathrm{OW}={\left|s\right|}^2-{\left|\omega \right|}^2.$$

It was independently introduced by [39,40]. For a two-dimensional flow $\underline{u}=(u,v)$ it turns out that

$$\begin{array}{c}\hfill \mathrm{OW}={\left(\frac{\partial }{\partial x}u\right)}^2+{\left(\frac{\partial }{\partial y}v\right)}^2+2\left(\frac{\partial }{\partial y}u\right)\left(\frac{\partial }{\partial x}v\right).\end{array}$$

By definition $\mathrm{OW}<0$ whenever the rotation tendency exceeds the strain one.

The local version of the $\mathrm{OW}$ parameter, called the local Okubo–Weiss parameter $\left(\mathrm{LOW}\right)$ (see [10]), depends on a positive distance $a>0$ and is defined as the integral of $\mathrm{OW}$ over the disk of radius a:

$$\mathrm{LOW}\left(\underline{x}\right)={\int }_{B_a\left(\underline{x}\right)}\mathrm{OW}\left({\underline{x}}^{\prime }\right)d{\underline{x}}^{\prime }.$$

2.2.2. Local Normalized Angular Momentum and Momentum Flux Fields

In the rotating rigid-body analogy the angular momentum of a fluid particle has to be maximized about the eddy center, as pointed out by [41]. This consideration suggested to define the local normalized angular momentum field $\left(\mathrm{LNAM}\right)$:

$$\mathrm{LNAM}\left(\underline{x}\right)=\frac{\widehat{z}·{\int }_{B_a\left(\underline{x}\right)}({\underline{x}}^{\prime }-\underline{x})\times \underline{u}d{\underline{x}}^{\prime }}{{\int }_{B_a\left(\underline{x}\right)}\left(|\underline{u}\left|\right|{\underline{x}}^{\prime }-\underline{x}|+|\underline{u}·({\underline{x}}^{\prime }-\underline{x})|\right)d{\underline{x}}^{\prime }},$$

which assumes extreme values $\pm 1$ at the centers of circular symmetric eddies: $+1$ for cyclonic rotations and $-1$ for anticyclonic ones (in [41] the term $\underline{u}·({\underline{x}}^{\prime }-\underline{x})$ appears with its sign; we added the modulus to get $\left|\mathrm{LNAM}\right|\le 1$.)

Analogously, the local normalized momentum flux field $\left(\mathrm{LNMF}\right)$ can be defined as follows:

$$\mathrm{LNMF}\left(\underline{x}\right)=\frac{{\int }_{B_a\left(\underline{x}\right)}\underline{u}·({\underline{x}}^{\prime }-\underline{x})d{\underline{x}}^{\prime }}{{\int }_{B_a\left(\underline{x}\right)}\left(|\underline{u}\left|\right|{\underline{x}}^{\prime }-\underline{x}|+|\underline{u}\times ({\underline{x}}^{\prime }-\underline{x})|\right)d{\underline{x}}^{\prime }}.$$

It is clear that $\mathrm{LNMF}$ identically vanishes on centers of rotating eddies, while it assumes extreme values $\pm 1$ at the symmetric sources and sinks; so it can be adopted to distinguish these various types of recirculating structures.

3. Methods

3.1. Eddy Detection Algorithms

We implemented two versions of two different existing detection algorithms for our study. The first method, the angular momentum eddy detection and tracking algorithm (AMEDA), developed by [10], was tested on several products such as altimeter data, numerical simulations and laboratory experiment. The second, proposed by [11], the ’Nencioli et al. algorithm’ (NEAL), was specifically designed for certain HF radar derived datasets.

It is worth noting that in both cases above the velocity fields utilized for testing and application were geostrophic or quasi-geostrophic. On the other hand the surface flow observed in the GoN is highly non-geostrophic and significant variations of the divergence field frequently occur, often associated to recirculating sources or sinks. So, to distinguish similar structures in our study area, it was necessary to modify those algorithms, and yet, as discussed in the following, our proposed refinements led to just moderate improvements. Therefore, in order to specifically address the aforementioned classification problems, we defined a third method, yet another eddy detection algorithm (YADA), inspired by [10,12].

3.2. Ameda

The AMEDA algorithm ([10]) determines the eddy centers accordingly with the following procedure:

1.

Identifies grid points which are local extrema of $\mathrm{LNAM}$ satisfying $\mathrm{LNAM}>\mathrm{K}$ and $\mathrm{LOW}<0$, for a chosen threshold $\mathrm{K}\in (0,1)$;

2.

Verifies the existence of at least one closed streamline around each extremum.

However, as already pointed out, GoN eddies may have hyperbolic orbits, in contrast with the geostrophic flows found in [10,11]. In such cases the second assumption is never verified, so we decided to adopt the following alternative criterion (described in [11]):

2’.

Confirms that the velocity field constantly rotates along the perimeter of the square domain of edge $2b$ and centered at the extremum, for a chosen distance b.

The modified version of AMEDA, obtained by substituting 2 with 2’, is here denoted by AMEDAmod.

3.3. Neal

The eddy detection algorithm developed in [11], and here denoted by NEAL, identifies the eddy centers in several steps, namely:

1.

Identifies couples of adjacent grid points $({\underline{x}}_1,{\underline{x}}_2)$ such that the meridional component of the velocity field changes sign going westward along the zonal segment of length $2a$, centered at ${\underline{x}}_i$, and increases its magnitude away from this point. This computation also provides the expected sign of rotation;

2.

Verifies that, at any such grid point ${\underline{x}}_i$, the zonal component of the velocity field changes sign going northward along the meridional segment of length $2a$, centered at ${\underline{x}}_i$, and increases its magnitude away from this point. This change must be compatible with the expected rotation;

3.

Identifies the $\mathrm{KE}$ (kinetic energy) local minima inside a square domain of edge $2b$, centered at ${\underline{x}}_i$, which are global minima in a square neighborhood $Q_b$ of the same size;

4.

Confirms that the velocity field constantly rotates along the perimeter $\partial Q_b$.

3.4. Yada

The YADA algorithm searches for potential eddy centers in two steps:

1.

Identifies the local extrema of a dynamical field like $\mathrm{LNAM}$, $\mathrm{KE}$ or $\mathrm{OW}$;

2.

Analyzes the streamline geometry within some neighborhood $Q_b$ of each extremum, ensuring the existence of either bounded hyperbolic orbits (characterizing eddies with sink-like cores) or elliptic orbits (in presence of eddies having stable orbits).

Note that the second step is precisely designed to distinguish different eddy geometries. During this classification procedure, as we will see in the next section, the YADA algorithm computes quantities that are strongly related to the eddy shape, and therefore provide useful information about its character, which may be either hyperbolic or elliptic, depending on the streamline behavior.

3.5. Tuning Strategy

Each algorithm depends on some parameters, specifically the $\mathrm{LNAM}$ threshold $\mathrm{K}$ and the neighborhood radii a and b, which have to be tuned in order to maximize the probability of detection. In principle, such a training phase should be carried out with a set of completely characterized observations, for which the real eddy population and its spatio-temporal distribution is perfectly known. This is never the case for eddy detection studies. In [10] the authors, in order to cross-validate their parametric algorithm, considered the number of detected eddies as a score function depending on the algorithm parameters. The best model was then chosen by looking for parameters stabilizing the score function. The reasoning behind this approach can be heuristically described as follows. One starts with an inaccurate model which predicts too few (or too many) eddies. However, by randomly exploring different parameter values, one may observe an increase (decrease) of the score function until reaching a stable region in the parameter space. Then, elements within the stable region can be considered optimal assuming that the observed local fluctuations are caused by the existence of eddies, that randomly fall in (or escape from) the detection range as parameters vary. In our study we chose to adopt the same tuning strategy, better described in the next section.

4. Results

In this section we first describe the tuning procedure for each chosen algorithm and then we discuss the results. Before doing this, some observations about the algorithm definitions are needed. Firstly, for numerical convenience, we substituted the disk $B_a\left(\underline{x}\right)$ in the definition of $\mathrm{LNAM}$ and $\mathrm{LOW}$ with the square domain centered at $\underline{x}$ of edge $2a$, which we denote by $Q_a$. Secondly, we note that in both algorithms AMEDA and NEAL the final step concerns the rotation of the velocity vector along a boundary profile. This was explicitly done by following the path counter-clockwise and verifying that any velocity vector at a given grid point was rotated to the left of the previous by an angle less than $\pi /2$ radians; note that this criterion does not depend on the sense of rotation of the velocity field along the path.

4.1. Ameda Tuning and Results

Three parameters have to be determined to run this algorithm: a, from the definition of $\mathrm{LNAM}$ and $\mathrm{LOW}$, $\mathrm{K}$ and b. To obtain all dimensionless parameters we divided a and b by the length scale l of one pixel ($l\sim 0.5$ km): $a_0=a/l$ and $b_0=b/l$.

The optimal choice of these parameters depends on the scale analysis of the investigated dynamics: if $a_0$ is too large then $\mathrm{LNAM}$ may sum up the contribution of many eddies inside $Q_a$, leading to a wrong estimate of the angular momentum. Similarly a large $b_0$ is not recommended, nor is a small one since the velocity vector may abruptly rotate with an angular velocity greater than $\pi /2$ radians per pixel in proximity of the eddy center. The parameter $\mathrm{K}$, in turn, once $a_0$ is coherently chosen, represents a lower bound for the detected eddy intensity.

We ran the algorithm on the 10-day dataset described in Section 2.1 for different values of the parameters $a_0$ and $b_0$, and analyzed the number of detected eddies $\mathrm{Ne}$ as a function of $\mathrm{K}$, varying from $0.1$ to 1 with step $0.1$. The results are shown in Figure 2.

For any choice of $a_0$ and $b_0$ the values of $\mathrm{Ne}$ turned out to be approximately constant for $\mathrm{K}<0.6$, so we set $\mathrm{K}=0.6$. On the other hand for a fixed $a_0$ the maximum of $\mathrm{Ne}$ was achieved at $b_0=2$; so we chose this value for $b_0$. Finally we noted that $\mathrm{Ne}$ weakly decreased as $a_0$ increased, as expected, suggesting to take $a_0=1$. In summary, our optimal choice of the parameters turned out be $(a_0,b_0,\mathrm{K})=(1,2,0.6)$.

Since we were interested in discriminating diverging structures from converging ones we added a third control to AMEDA (see above, Section 3.4):

3.

Discards those extrema satisfying $\mathrm{LNMF}>0.2$.

In this way we allowed only a little divergence near the eddy core (see the $\mathrm{LNMF}$ contour line in Figure 3 for instance). This correction reduced the number of detected eddies $\mathrm{Ne}$ by about 16% for $\mathrm{K}=0.6$, and by 0.4% for $\mathrm{K}=0.7$; this behavior was expected since strong rotations often imply weak divergences.

Unfortunately this criterion is not optimal: It is a pure dynamical control depending on the local behavior of the flow, but eddies are extensive structures which may admit internal divergences. In such a case the eddy center and its real extension is difficult to estimate since it would be necessary to understand the streamline geometry.

4.2. Neal Tuning and Results

By definition NEAL is a purely geometrical method, which is not required to compute any differential quantity: Eddy centers are simply defined as energy minima. Of course this reduces the computation time, making the algorithm fast and efficient. Moreover we note that, as in the previous case, there are two parameters, a and b, to be determined; as before we considered the dimensionless parameters $a_0=a/l$ and $b_0=b/l$.

We ran the algorithm on the dataset for $a_0=1,\dots ,8$ and $b_0=1,\dots ,8$. In Figure 4 the number of eddies $\mathrm{Ne}$, discarding the unlikely results obtained for $a_0=1$ ($\mathrm{Ne}>1000$), is shown. We observed that for $a_0=2$ there was a weak dependence on $b_0$, but the values of $\mathrm{Ne}$ turned out to be much less than those obtained by AMEDA. For $a_0=3,4$ the number of detected eddies highly depended on $b_0$, but the results did not converge anywhere; for $a_0>4$ we obtained values depending weakly on $b_0$ but much less than those for $a_0=2$. These discrepancies were likely caused by asymmetrical eddies lacking radially increasing velocity components. In conclusion, we were not able to tune NEAL, as no stable regions in the parameter space were identified.

4.3. Yada Tuning and Results

The first step of the algorithm coincides with that of AMEDA: it identifies any local extremum $\underline{x}$ of $\mathrm{LNAM}$ satisfying $\mathrm{LNAM}>0.6$ for $a_0=1$ (having tested this values in tuning AMEDA).

The second step concerns the study of the streamline geometry in a neighborhood of the extremum. It proceeds as follows: in a square neighborhood $Q_b$ centered at $\underline{x}$ with edge $2b$, where the length b has to be intended as an upper limit for the eddy radius (which, in this study, has been overestimated to be $b=10l$), it draws a circle $C_r$ of radius $r=l$, centered at $\underline{x}$ and composed by 8 points (as many as the grid points on the tangent square perimeter). It then computes the streamlines originated from these points (each streamline is built by means of a fourth order Runge–Kutta method, with a step of 5 points per pixel. It is composed by up to 1000 points), collecting their mean points (geometric means) and end points.

Then the algorithm performs a selection of all the streamlines such that:

(1)

The end points belong to the square domain $Q_{b-2l}$ (that is: they stay away from the boundary of the reference domain);

(2)

Each streamline completes at least one revolution.

The second control consists in looking at the cumulative winding-angle (given an oriented piece-wise linear curve, its cumulative winding-angle is the sum, over all the angular points, of the angle, with positive sign going counter-clockwise and negative going clockwise, between the two intersecting segments, considered as vectors) of the streamline, as defined in [12]: it has to be, in modulus, equal to or grater than $2\pi$. If no such streamline exists we increase the radius of $C_r$ by l until at least one streamline satisfying (1) and (2) is found; the maximum allowed r will be $b/2$ (at any step we increase the number of points in the circle to match the amount of grid points in the tangent square perimeter).

Note that if one such streamline exists it means that either it converges to some point inside the domain or it definitely stays inside the domain without converging anywhere (at least for the first 1000 points). Of course some diverging streamline, which rotates without reaching the boundary of the domain, could exist and be identified by the algorithm. However, a path starting from $\underline{x}$ and which rotates around it at least three times before reaching the boundary, and having the same step-size of the drawn streamlines, counts approximately 300–400 points. Then, if a spiral-like streamline diverging from the center stays inside the domain without reaching the boundary, it has to complete at least eight revolutions; even in this case we can safely affirm that an eddy exists.

Once the algorithm has selected all the streamlines satisfying (1) and (2) for the first allowable r, it compares the distributions of the mean points with that of the end points. If the eddy core behaves as a sink all the end points will accumulate near it. On the other hand if the orbits around the eddy are elliptic the mean points will be close to the orbits’ common center of mass. So the algorithm chooses the distribution with less variance and choose its mean point as eddy center of mass, or eddy symmetry center (ESC); by contrast the extremum will be called the eddy extreme point (EEP). However, to ensure it is not selecting another eddy in the square domain relative to a different extremum, it is required that the expected ESC must belong to the disk bounded by $C_r$, otherwise the point is discarded and the algorithm moves toward the next extremum; some examples of this procedure can be found in Figure 5 and Figure 6.

Generally the $\mathrm{ESC}$ does not coincide with the eddy center even though it provides a better approximation of the true eddy core than the $\mathrm{EEP}$; e.g., Figure 5, Figure 6, Figure 7 and Figure 8. As a consequence the distance between the ESC and the EEP can be considered as a measure of the eddy asymmetry.

Following the procedure just described, the algorithm detected $\mathrm{Ne}=255$ eddies, about 30% more than the value obtained with AMEDA. Eddies such as those in Figure 5, for instance, were missed by AMEDA due to their small extension and asymmetry, whereas they were detected by YADA. However there were still structures detected by AMEDA and missed by YADA, see for instance Figure 9. In some of these cases we noted that the divergence around the $\mathrm{LNAM}$ extremum was so weak ($\mathrm{LNMF}<0.2$) that some orbits complete up to three revolutions before leaving the region.

In conclusion we can affirm that YADA was able to detect and distinguish multiple kinds of eddies and, as it will be shown in the next part, it can be refined to estimate their boundaries.

4.4. Eddy Boundaries

There is no universal definition of eddy boundary: many authors adopted $\mathrm{OW}$ or $\omega$ contour lines, as well as closed streamlines or closed stream-function contours (not equivalent at all) to locate them.

Based on YADA architecture, we propose a different definition, which aims to distinguish eddies with sink-like cores from those having elliptic orbits. Of course we can not expect to identify the true boundary profile, so we assume it to be in general elliptic (rather than circular).

4.4.1. Sink-Like Cores

We considered the set $S_r$ of all the streamlines originated from $C_r$ and satisfying conditions (1) and (2) as explained in the definition of YADA. We then evaluated the variance ellipse of this distribution of points; let e be its eccentricity. Then we drew the ellipse $E_d$ of eccentricity e, centered at the $\mathrm{ESC}$, with major semi-axis $d=l$. As we did for $C_r$ we consider the streamlines emanated by $E_d$ and if all such streamlines belong to the ellipse interior we increment d by l, repeating the step up to reach $d=b$. Further, in analogy with [10], we also control that the circulation along $E_d$ does not decrease by increasing d. The largest ellipse $E_d$ satisfying this criterion will define the eddy boundary, as shown in Figure 7.

4.4.2. Eddies Having Elliptic Orbits

For such eddies we also started by building the variance ellipse of the admissible streamlines $S_r$. Then we drew the ellipses $E_d$ with eccentricity e, centered at the ESC and having semi-major axis $d=l,2l,\dots ,d^{\prime }$, where $d^{\prime }$ was the maximum distance for which the circulation around $E_d$ was a non-decreasing function of d, and we moved each $E_d$ following the flow, thus collecting all the end points of the streamlines emanated by $E_d$. We denoted this set by $\epsilon \left(E_d\right)$.

We expected that, if $E_d$ approximated the eddy boundary, it had to be close to an elliptic orbit, and therefore $ϵ\left(E_d\right)$ had to be a small deformation of $E_d$. However, in order to ignore the effects of translating motions, which could occur, we centered the two sets on the same reference point. Then we evaluated the Hausdorff distance $\delta \left(d\right)$ between them (see the Appendix A for details).

Finally we took $d^{*}$ satisfying $\delta \left(d^{*}\right)=\min \left\{\delta \left(d\right)\right\}$, and $E_{d^{*}}$ as eddy boundary; we chose $E_{d^{*}}$ to keep the elliptic symmetric, though $ϵ\left(E_{d^{*}}\right)$ would provide a better approximation. In Figure 8 we plotted the various steps just described; in each panel the ellipse of semi-major axis $d=l,2l,\dots ,d^{\prime }$ is drawn.

5. Discussion

5.1. Detected Eddies

In Section 4 we tried to tune the three chosen algorithms by following a stability criterion. We succeeded for AMEDA, but failed for NEAL. Indeed, in the latter case, no stable parameter regions were identified. The algorithm YADA, instead, was indirectly tuned by using the AMEDA common parameters, namely K and a; in fact both these parameters served to set a lower bound to the eddy rotational energy, which was independent on the algorithm itself.

We then compared the tuned version of the two algorithms, AMEDA and YADA. It turns out that AMEDA detected 195 eddies within the time period, whereas YADA detected 255 eddies. However, among these, 157 eddies have been identified by both, leaving 38 eddies detected by AMEDA but missed by YADA and 98 seen by YADA but lost by AMEDA. Mismatches between AMEDA and YADA detections were expected, as already observed: eddies like that in Figure 9 were missed by YADA due to their large extension and weak, but still positive, divergence. On the other hand, deformed recirculations, as in Figure 5, were easily hidden to AMEDA but not to YADA.

Finally we checked by visual inspection all the available time frames, in order to determine the existence of false positive detections. Interestingly, no such detections were found, testifying the reliability of both the algorithms, at least in terms of false alarms. The same inspection showed that volatile and higly asymmetrical structures were still missed by both. However, our algorithm was able to detect long-lived eddies for longer time periods, as shown in Figure 10.

5.2. Equivalent Radii

Following [10] we computed the equivalent radius $\rho$ for each detected eddy. It is defined as the radius of the circle bounding an area equivalent to that delimited by the eddy boundary. For elliptic contours it equals $d\sqrt[4]{1-e^2}$. The mean radius $\overline{\rho }$ turned out to be $0.87$ km, with a standard deviation of $0.84$ km and values of $2.8$ and $3.6$ km for the 95th and 99th percentile respectively. Similarly we computed a mean eccentricity $\overline{e}$ of $0.71$ with standard deviation of $0.02$. It turned out that the mean equivalent radius was merely 1–2 times the pixel length scale of the dataset, and therefore we could expect that our method would not accurately describe some kinematic and dynamic features of eddies having $\rho$ close to $\overline{\rho }$. It may have been possible to obtain a more accurate description by increasing the spatial resolution up to reach $l\sim 0.3$ km; however this would have implied performing interpolations at a much higher resolution.

5.3. Spatial Distribution

The hourly sampling frequency of the HF radar allowed to track eddies having longer lifetime. We identified such long-lived structures by looking for eddies encircling an EEP, coming from the previous temporal frame, within their own boundary. The spatial distribution of all the detected long-lived eddies, counted without repetitions, can be found in Figure 11.

A larger density can be noted in correspondence of a relatively flat plateau located in ${40.73}^{\circ }$ N, ${14.27}^{\circ }$ E, between 120 and 160 m of depth, excluding topographic wakes, that need steep bathymetric slopes, as primary instability causes (for a comprehensive analysis of several submesoscale eddy generation mechanisms see [5]). To understand the instability sources generating the GoN eddies, therefore, it would be necessary to investigate the flow behavior within the SBL (surface boundary layer). Unfortunately there are neither wind observations nor density profiles relative to the GoN SBL. However, there is a work in progress, funded by the Science and Technology department of the Parthenope University of Naples, aiming to investigate the vertical water profile through numerical simulation. Such a study could provide more information to understand the instability sources within the GoN.

Finally we observed that the detected long-lived eddies, namely those with lifetimes greater than 1 h, were 36, distributed as shown in Figure 11. They usually persisted for few hours, 5 or 7 h in some cases, distributed in agreement with the entire density population. We also noted that, except for few examples, they were almost stationary.

6. Conclusions

Submesoscale motions play an important role in the transfer of energy from the mesoscale down to the dissipative range ([5,42]) as well as in the transport of pollutants, of biomass, of organic and inorganic matter ([43,44]). At present, they represent one of the frontiers of the study of transport in the ocean. On the other hand, as recently pointed out by several authors (see, e.g., [5,8,45]), the observation of submesoscale eddies in a synoptic way is challenging, feasible with remote sensing techniques which are typicaly limited by available resolution. HF radars are land-based remote sensing tools that can be very suitable for such investigations, given their temporal and spatial sampling characteristics. In this paper we have tackled the issue of devising an algorithm for submesoscale eddy detection in a high resolution surface velocity field provided by a network of 25 Mhz coastal radar antennas active in the Gulf of Naples. We started by applying two different eddy detection algorithms, here denoted by AMEDA and NEAL, based on the studies of [10,11] respectively, but they both displayed some weaknesses. The application of AMEDA to the selected surface current dataset demonstrated to be unable to distinguish submesoscale eddies entrapping fluid masses from the others. So we refined the algorithm by measuring the divergence occurring in the eddy core. The number of detected eddies then decreased. Differently, we did not succeed to tune the algorithm NEAL.

To obtain a more efficient detection method, able to distinguish asymmetric eddies entrapping fluid masses, we developed a novel, modified algorithm, named YADA, which detected 255 eddies (about 30% more than the refined AMEDA value). Then we used YADA to estimate the eddy boundaries, assuming an elliptical symmetry, and we found a mean equivalent radius of $0.87$ km and a mean eccentricity of $0.71$.

YADA’s results were validated comparison with the results of the algorithm AMEDA, as well as by visual inspection of all time frames. Having developed a more robust algorithm, this also allowed us to look at the spatial distribution of the detected eddies, and to observe a larger density at the plateau located at 160 m of depth, and led us to exclude topographic wakes as main instability sources. Moreover, we obtained estimates for their spatial scales taking into account the noncircular geometry of the vortices.

As mentioned above, submesoscale eddies represent a relevant transport mechanism for waters and their biogeochemical characteristics; their influence is particularly important in those coastal areas, such as the Gulf of Naples, characterized by the coexistence of different subsystems, whose mutual exchanges may strongly affect the whole functioning of the area. For this reason an accurate identification of such structures is a necessary first step for the quantitative assessment of their role, which we plan to further investigate in terms of their specific transport properties both in the horizontal and in the vertical.