Next Article in Journal
Assessing Typhoon-Induced Canopy Damage Using Vegetation Indices in the Fushan Experimental Forest, Taiwan
Next Article in Special Issue
Accuracies of Soil Moisture Estimations Using a Semi-Empirical Model over Bare Soil Agricultural Croplands from Sentinel-1 SAR Data
Previous Article in Journal
Enhancing Methods for Under-Canopy Unmanned Aircraft System Based Photogrammetry in Complex Forests for Tree Diameter Measurement
Previous Article in Special Issue
Applications of UAV Thermal Imagery in Precision Agriculture: State of the Art and Future Research Outlook
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 12
Issue 10
10.3390/rs12101653
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

To Blend or Not to Blend? A Framework for Nationwide Landsat–MODIS Data Selection for Crop Yield Prediction

by
Yang Chen
1,*,
Tim R. McVicar
2,
Randall J. Donohue
2,
Nikhil Garg
1,
François Waldner
3,
Noboru Ota
4,
Lingtao Li
2 and
Roger Lawes
4
1
CSIRO Data61, Goods Shed North, 34 Village St, Docklands, VIC 3008, Australia
2
CSIRO Land and Water, GPO Box 1700, Canberra, ACT 2061, Australia
3
CSIRO Agriculture and Food, 306 Carmody Rd, St Lucia, QLD 4067, Australia
4
CSIRO Agriculture and Food, 147 Underwood Ave, Floreat, WA 6014, Australia
*
Author to whom correspondence should be addressed.
Remote Sens. 2020, 12(10), 1653; https://doi.org/10.3390/rs12101653
Submission received: 1 May 2020 / Revised: 19 May 2020 / Accepted: 19 May 2020 / Published: 21 May 2020
(This article belongs to the Special Issue Remote Sensing in Agriculture: State-of-the-Art)
Browse Figures
Versions Notes

Abstract

:
The onus for monitoring crop growth from space is its ability to be applied anytime and anywhere, to produce crop yield estimates that are consistent at both the subfield scale for farming management strategies and the country level for national crop yield assessment. Historically, the requirements for satellites to successfully monitor crop growth and yield differed depending on the extent of the area being monitored. Diverging imaging capabilities can be reconciled by blending images from high-temporal-frequency (HTF) and high-spatial-resolution (HSR) sensors to produce images that possess both HTF and HSR characteristics across large areas. We evaluated the relative performance of Moderate Resolution Imaging Spectroradiometer (MODIS), Landsat, and blended imagery for crop yield estimates (2009–2015) using a carbon-turnover yield model deployed across the Australian cropping area. Based on the fraction of missing Landsat observations, we further developed a parsimonious framework to inform when and where blending is beneficial for nationwide crop yield prediction at a finer scale (i.e., the 25-m pixel resolution). Landsat provided the best yield predictions when no observations were missing, which occurred in 17% of the cropping area of Australia. Blending was preferred when <42% of Landsat observations were missing, which occurred in 33% of the cropping area of Australia. MODIS produced a lower prediction error when ≥42% of the Landsat images were missing (~50% of the cropping area). By identifying when and where blending outperforms predictions from either Landsat or MODIS, the proposed framework enables more accurate monitoring of biophysical processes and yields, while keeping computational costs low.

Graphical Abstract

1. Introduction

The world’s human population is projected to increase by more than 35% by 2050 [1]. To contribute to improved global food security, the next generation of crop models and agricultural decision support tools needs to efficiently and consistently operate across various scales [2]. Accurate nationwide crop yield forecasts may ensure food security to the citizens. More accurate crop yield prediction at the subfield scale can provide farmers with more detailed information for guiding, within the growing season, in-field variable rate applications of fertilizer, herbicides, and pesticides. An efficient approach to monitor crop growth uses satellite observations providing repeated synoptic regional assessments [3,4,5,6]. High-temporal-frequency (HTF) observations are required to accurately track crop development [7] and predict yield [8], and high-spatial-resolution (HSR) observations are necessary to capture within-field heterogeneity [9].
There is a trade-off between temporal frequency and spatial resolution [10,11,12] as no single sensor can regularly image vast areas of the Earth used for nation-wide dryland cropping at a high spatial resolution. Commercial options of products combine HTF and HSR images achieved by increasing the number of satellites in orbit, such as PlanetScope; however, such commercial options are not affordable for national-scale monitoring, especially in a country as large as Australia (7.7 million km2), with the southern Australian cereal-based agricultural system notionally covering 530,000 km2 [13]. The Moderate Resolution Imaging Spectroradiometer (MODIS) provides complete coverage of the globe every day at a 250-m spatial resolution from red and near-infrared bands. This resolution constrains the capacity of describing cropping systems, crop growth, and field heterogeneities, especially when fields are small-to-moderate sized and landscapes are fragmented [14,15]. Sensors with higher spatial resolution, such as Sentinel-2 or Landsat, are more suitable for these smaller fields/management units, but their lower temporal frequencies limit their ability to capture rapidly evolving crop processes, especially when factoring in the potential clouds [16]. Lobell et al. [17] used valid Landsat observations (cloud cover <10%) during the growing season to generate optical-based vegetation indices (Vis) and then fitted a multilinear regression between these VIs and a large number of Agricultural Production Systems Simulator (APSIM) simulations for yield prediction. In a country like Australia, most of the arable non-irrigated land grows winter wheat, barley, oats, and canola, and their growth depends on the in-season rainfall; therefore, totally cloud-free time-series observations for their entire growing season are infrequent.
To overcome these challenges, various methods for spatial filtering [18], temporal gap-filling [19,20,21], and data fusion [22,23,24] were devised with a varying degree of success. As spatial filtering and temporal gap-filling disregard the spatial and temporal correlation of a pixel, they are highly sensitive to the choice of size/length of the spatial/temporal window [20,25]. Data fusion techniques, on which this article focuses, were shown to improve the temporal resolution of fine-spatial-resolution data by blending observations from sensors with different spatial and temporal characteristics. Prominent examples are the Spatial and Temporal Adaptive Reflectance Fusion Model (STARFM; Gao et al. [12]) and the Enhanced STARFM (ESTARFM; Zhu et al. [11]). However, blending is no “silver bullet”, as it often introduces unforeseen spatial and temporal variances [10]. Therefore, it is critical to systematically evaluate the benefits of blending and identify where and when blending helps to improve monitoring.
Blending satellite data with complementary frequency and spatial resolution characteristics, such as MODIS (herein considered as an HTF and low-spatial-resolution (LSR) sensor) and Landsat (herein considered as a low-temporal-frequency (LTF) and HSR sensor), provides a solution of synthetic imagery that is both HTF and HSR [26]. Current literature such as Dong et al. [27] found that using Landsat images provides a higher crop yield prediction accuracy for field scales over MODIS images, and a further improvement can be achieved by combining Landsat and MODIS (L–M) blended data with the incomplete Landsat series. To date, the utility of blended output is not yet tested for regional and national crop yield mapping [28,29,30,31,32,33,34,35] (Table 1); this study fills that niche.
This study quantifies and evaluates the benefits of blending satellite data of different temporal frequencies and spatial resolutions for crop yield prediction. The specific objectives of this study are to (i) estimate yields using MODIS, Landsat, and L–M blended data and then compare the yield prediction at both pixel and field scales, (ii) identify the fraction of missing Landsat data during a growing season considering the 16-day acquisition cycle to determine a threshold where the blended data can improve the prediction, and (iii) quantify the improvements in the yield prediction accuracy based on the threshold.

2. Study Area and Data

2.1. Study Area

The southern Australian agricultural system is dominated by dryland agriculture where cereals (e.g., wheat, barley, and oats), oilseeds (e.g., canola), and legumes (e.g., lupins, chickpeas, field peas, and soybeans) are planted, often in rotation with annual pastures and fallows. Australian wheatbelt (Figure 1) spans an extremely variable agroecological environment with respect to the climate across the continent, leading to the high spatial variability in Australian grain production. The precipitation varies enormously across the country (Figure S1, Supplementary Materials); winter (June–August) precipitations are dominant in Western Australia and South Australia, while summer (December–February) precipitations are dominant in Queensland and northern New South Wales. In southern New South Wales and Victoria, total precipitation is more uniformly distributed throughout the seasons where summer precipitation is more intense indicating that winter precipitation is more frequent [36]. Long-term average monthly accumulated precipitation records strongly correlate with the average number of rainy days (Figure S1, Supplementary Materials).

2.2. Data

2.2.1. Satellite Images and L–M Blended Data

Time series of Landsat-5 Thematic Mapper (TM), Landsat-7 Enhanced Thematic Mapper (ETM)+, and Landsat-8 Operational Land Imager (OLI) and Thermal Infrared Sensor (TIRS) standardized surface reflectance data are sourced from Geoscience Australia (http://geoscienceaustralia.github.io/digitalearthau/index.html), which contains 239 scenes covering the Australian wheatbelt across seven years (2009–2015). These images are nadir-corrected, adjusted for bidirectional reflectance distribution function, and topographically corrected followed by Li et al.’s methods [38], resulting in a 25-m pixel resolution. This is as, in Geoscience Australia’s processing stream, they oversample the Landsat imagery to 25 m to allow easier integration with other remote sensing data sources. Time series of normalized difference vegetation index (NDVI) are then computed using the red and near-infrared bands [39]. The 16-day composite of MODIS NDVI (MOD13Q1 v006) data are used due to the low clouds, low view angle, and the highest NDVI value at 250-m spatial resolution. The MODIS data are sourced from United States Geological Survey for the corresponding periods and area (16 tiles) and are then downscaled to 25 m by 25 m spatial resolution using nearest neighbor interpolation [40] for input to the blending algorithm and for consistency to enable further analysis.
The inter-annual variability of precipitation (Figure 2b) illustrates that the probability of rain days is higher during June–August (i.e., tillering to flowering phase), which is a critical period for crop yield prediction [41,42]. Figure 2b also shows the value of 0.58 in July at the 75th quartile, which indicates that the probability of cloud-free Landsat images could be lower than 42% in most areas. Here, 75% of field-scale Landsat missing data occur during the growing season (i.e., 113–289 days of the year (DOY)), and only 25% of the Landsat data are complete sequences (Figure 3).
To blend MODIS and Landsat NDVI data and create the 16-day time series of gap-filled Landsat-like images, we applied ESTARFM [11], which is superior when the spatial variance is dominant [10]. We follow Jarihani et al.’s [22] recommendation to “index then blend”, as it yields more accurate results and provides higher computational efficiency than the “blend then index” approach. Figure S2 (Supplementary Materials) illustrates the blending process and the resulting Landsat-like image. As a result of data blending, each pixel is described by 22 observations across the calendar year. For more details about ESTARFM see [11,43].

2.2.2. Yield Data

Australia’s major dryland crops are selected for yield estimates and validation, including 35 fields of canola, 123 fields of wheat, and 52 fields of barley (Table S1, Supplementary Materials). The average area of these fields is ~112 ha with a standard deviation of ~69 ha. Using various yield monitoring systems mounted on grain harvesters operated by farmers, these observed data were collected at these sites across the country from 2009 to 2015 (Figure 1). The data obtained by these commercially available yield monitors were used to construct a yield data image at 5-m resolution [44], which was upscaled to 25 m and 250 m to match the Landsat and MODIS resolutions, respectively.

2.2.3. Climate Data

Climate data were sourced from Science Information for Land Owners (SILO) which provides nationwide meteorological variables (e.g., maximum and minimum air temperature, and precipitation) at daily temporal frequencies by interpolating observations made by the Australian Bureau of Meteorology onto a 0.05° by 0.05° grid [37].

3. Methods

3.1. Yield Prediction

We use a semi-empirical model [C-Crop; 6]) because of its low data requirements for calibration across large areas. C-Crop correlates actual grain weight (t/ha) to end-of-season above-ground plant carbon mass (C), and the estimation of C is based on biophysical principles of plant photosynthesis [6]. C i is estimated using the carbon mass ( C i − 1 ) from the previous time step and the current period’s allocated net assimilation flux N i (gCm−2) minus the dead biomass that enters the litter store, and i (1–22) is the model time step (every 16 days in a calendar year).
C i = ( 1 − ρ ) ( C i − 1 + N i )
where ρ (periods−1) is the reciprocal of carbon longevity (i.e., the turn-over rate of plant live carbon into senesced tissue per time step i).

3.1.1. Net Primary Productivity

Net primary productivity (NPP) is the rate of carbon assimilation from atmospheric CO2 to organic material (biomass) for a given area while accounting for the energy loss due to autotrophic respiration [6,45].
N i = 0.75 ( G i f P A R i 0.95 − 16 r 10 C i − 1 c n σ i )
where f P A R i 0.95 is the fraction of total assimilation flux G i allocated to the above-ground plant biomass (gCm−2) at time step i. The plant maintenance respiration is calculated as a function of leaf nitrogen, air temperature, and previous biomass C i − 1 . r 10 is the plant tissue respiration rate at 10 °C; cn stands for plant carbon-to-nitrogen ratio; σ i is a scalar that modifies the respiration rate according to the daily air temperature [46].

3.1.2. Gross Primary Productivity

The total assimilation flux G i , = also known as the gross primary productivity (GPP) (gCm−2∙day−1), can be calculated using the remote sensing-based plant light use efficiency (LUE) approach. The chloroplasts use incoming solar radiation with a spectral range between 400 nm and 700 nm in photosynthesis [47].
G i = P A R i × f P A R i × R U E i
P A R = 2.3 ( R O × τ ∂ ) ρ s w
where ( R O × τ ∂ ) ρ s w represents the shortwave irradiance (Rs), R O is daily top-of-atmosphere shortwave irradiance (J/m2/day) [48,49], τ ∂ is atmospheric transmissivity calculated using the Bristow–Campbell relationship [50,51] calibrated for Australia, and ρ s w is the ratio of shortwave irradiance at a sloping surface to that at a horizontal surface [52].
fPAR is the portion of PAR that is absorbed by a photosynthetic organism, and it is estimated using a linear relation between fPAR and rescaled NDVI by thresholds (i.e., local minimum and crop-specific maximum NDVIs) [53,54]. LUE is highly linearly related to a diffuse fraction (fD) and photosynthetic carbon flux [55].
L U E i = 0.024 × f D i + 0.00061 A x
where A x is the maximum photosynthetic capacity (μmolCm−2∙s−1), which is a crop-specific parameter; is 23, 40, and 45 for barley [56], canola [57], and wheat [57], respectively; f D is the ratio of diffused to total solar irradiance varying from 0.2 (under clear skies) to 1.0 (under overcast skies) [48]. For a full description of C-Crop, see Donohue et al. [6].

3.2. Validation

Two sets of data are used for validation and further analysis, depending on the pixel-level completeness of time-series Landsat NDVIs at 25-m pixel resolution across the growing season (i: 8–19) between April (DOY 113) and October (DOY 304) (Figure S3, Supplementary Materials). Firstly, the coordinates of complete time-series Landsat pixels are used to obtain the resampled MODIS, L–M blended, and observed yield data for validation at the 25-m resolution as the first dataset. Secondly, these complete time-series Landsat pixels are upscaled at 250 m pixel size to extract the MODIS and the L–M blended data with the same pixel size for the validation at the moderate resolution. Thirdly, the pixel-level yield predictions are aggregated for each respective field by averaging the yield values of the pixels within, for field-level validation. Fourthly, and finally, the predicted yields are evaluated using the model coefficient of determination (R2), the root-mean-square error (RMSE), and the mean bias error (MBE). The R2 describes the proportion of the response variable that can be explained by the model. RMSE gives more weight to the largest errors, and the MBE indicates the systematic error of the model to under or overestimate. These procedures are then repeated for the second dataset created according to the coordinates of incomplete time-series Landsat NDVIs at the 25-m pixel resolution. As C-Crop requires a time series of NDVI, the results are assessed without the incomplete time-series pixels of Landsat.

3.3. Identification of Threshold for When to Blend

The incomplete time-series pixels of Landsat are gap-filled with the L–M blended pixels (LLM). The threshold to indicate when blending is beneficial is identified by quantifying the impact of the fraction of missing data on the prediction accuracy at 25 m. Firstly, we group MODIS and LLM time series in eight groups, based on the fraction of Landsat missing data (<10%, 10–20%, 20–30%, 30–40%, 40–50%, 50–60%, 60–70%, and 70–80%). Then, the accuracy of each group is analyzed by calculating the R2 and the RMSE. The performance of C-Crop using MODIS and LLM is compared by the fraction of missing data in Landsat across time. The threshold can be identified, when the model provides the same R2 and RMSE using LLM as with MODIS (Figure S3, Supplementary Materials). This threshold determines when, where, or how much L–M blended data improves crop yield prediction when the fraction of missing data in Landsat is lower than the identified threshold.

3.4. Evaluation of the Improvement in Yield Prediction Accuracy

The improvement in prediction accuracy using the identified threshold for multiple spatio-temporal data selection is statistically quantified. More specifically, the threshold is applied to the Landsat observations (2000–2018). Firstly, we compute the temporal probability of optimally using MODIS, Landsat, and LLM images for nationwide crop yield predictions during the past two decades, and then map the results to illustrate the spatial variability of multi-sensor data selection for 25-m pixel-level yield prediction across the wheatbelt. We then evaluate the area percentage of the data sources on a yearly basis and analyze their potential correlation to the annual precipitation (mm/year). Finally, the improvement in the accuracy of predicted yields is evaluated on the field level using MODIS and LLM for Western and eastern Australia, against the reported data [58]. The growing season of 2015 is selected due to the availability of a larger quantity of observed yield data. The incomplete 2015 Landsat series are gap-filled with the blended values corresponding to the threshold value.

4. Results

4.1. Yield Prediction

Exactly 66% of the observed fields have a complete time series of Landsat NDVIs at the pixel level across the growing season. For this dataset, C-Crop performs the best with Landsat images at field (R2 = 0.68; Figure 4a), 250-m (R2 = 0.85; Figure 4d), and 25-m (R2 = 0.48; Figure 4g) pixel resolutions for yield prediction pooled for wheat, barley, and canola. MODIS-based model yields were at least 10% less in terms of the R2 than when using complete time-series Landsat data. The model performs almost identically when using MODIS and L–M blended data for the predictions at both field and pixel scales. However, it produces the lowest bias for field (MBE = −0.32 t/ha; Figure 4c), 250-m (MBE = −0.23; Figure 4f), and 25-m (MBE = −0.21; Figure 4i) pixels when using the L–M blended data.
Figure 5 shows that 210 fields have incomplete time-series Landsat pixels during the growing season. These series are incomplete due to clouds in some of the Landsat images acquired in the specific growing season when the yield data are observed. Using this set of data, the L–M blended data-based model performs the same as the MODIS-based model when aggregating to 250-m (R2 = 0.86, RMSE = 0.52 t/ha, MBE = −0.40 t/ha; Figure 5c,d) and field (R2 = 0.66, RMSE = 0.82 t/ha, MBE = −0.49 t/ha; Figure 5a,b) scales. The L–M blended data-based model shows its advantages at the 25-m pixel level, which explains an extra 7% of the variability in the observed yields when the Landsat time-series pixels are incomplete (Figure 5e,f).

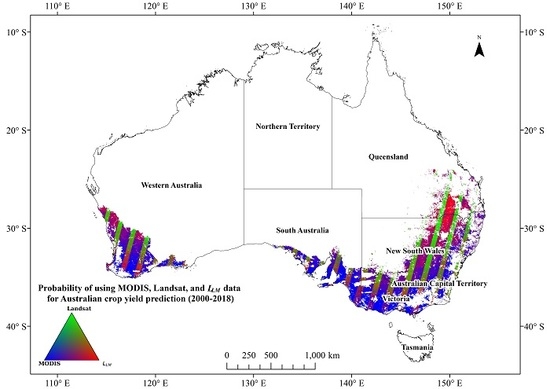
4.2. Identification of the Threshold

Figure 6a shows that the 25-m pixel-level yield prediction accuracy fluctuates between 0.35 and 0.75 using MODIS and LLM data in time and space, where time-series Landsat observations are incomplete. The R2 derived from MODIS is steady (between 0.4 and 0.5) where the fraction of missing Landsat data ranged between 0.05 and 0.42, which is lower than the R2 (0.62–0.5) derived from LLM data. The RMSE derived from both data sources remains approximately 0.9 t/ha for the same fraction of missing Landsat data (Figure 6b). When more incomplete time-series Landsat data are observed (from 0.42 to 0.75 on both Figure 6a,b), the R2 based on MODIS increases to around 0.7 and the RMSE decreases to 0.4 t/ha (as MODIS is not as cloud-affected as Landsat due to imagery being acquired on more days), whereas the R2 derived from the LLM fluctuates between 0.6 and 0.4 and the RMSE changes between 1.3 and 0.8 t/ha (Figure 6). Given this, up to 42% of missing Landsat data in the growing season is defined as the threshold for when L–M blending is optimal to implement. That is, the 25-m pixel-level yield prediction accuracy can be improved using LLM when the fraction of missing Landsat data at the coordinates is below this threshold. For instance, the LLM-based model increases R2 by up to 20% when the fraction of the missing Landsat data is below 42% (Figure 6a).

4.3. Evaluation of the Improvement in Yield Prediction Accuracy

Given the availability of cloud-free Landsat and MODIS data across the wheatbelt (2000–2018), in concert with the previously determined threshold (Figure 6) and finding (Figure 5), we can demonstrate which imagery (i.e., either MODIS, Landsat, and LLM) is best suitable for 25-m pixel-level crop yield prediction (Figure 7). Figure 7 shows the selection when using multiple satellite products for crop yield estimates across the wheatbelt over the past two decades. For the wheatbelt north of 35° south (S), there is a higher probability of obtaining complete cloud-free Landsat observations over the growing season in the east–west overlapping areas of adjacent Landsat Path-Rows, whilst LLM is optimal elsewhere north of 35° S. South of 35° S, MODIS is optimal, with LLM being optimal in the east–west overlapping areas of adjacent Landsat Path-Rows (in Figure 7).
For 25-m pixel-level yield prediction, blended data should be preferred on average for 33% of the Australian wheatbelt area (Figure 8a). MODIS and Landsat data remain the preferred data sources in 50% and 17% of cases, respectively. Figure 8b shows that the area percentage is positively correlated with annual precipitation for MODIS and negatively correlated for Landsat and the L-M blended data. MODIS has a larger scatter when annual precipitation is greater than 400 mm/year.
Of the 53-million-ha Australia wheatbelt, complete Landsat time series were suitable for 28.6% of that area, MODIS for 31.5%, and LLM for 39.9% during the 2015 growing season (Figure 8a). In this season, there are 104 fields available for assessing the accuracy improvement in yield prediction accuracy for nationwide crop yield prediction (Table S1, Supplementary Materials). Within these observed yield data, 69 fields are located where L–M blended images can improve the prediction accuracy according to the previously defined (see Figure 6) 42% Landsat missing data threshold. Figure 9 shows the predicted yields against the observed values for 63 fields in Western Australia (i.e., WA), and six fields in eastern Australia (i.e., Queensland (QLD), New south Wales (NSW), Victoria (VIC), and South Australia (SA)).
In these areas (see Figure 9), when the fraction of incomplete Landsat series across the growing season of 2015 falls below 42%, using LLM reduced the field-level yield prediction errors by 0.15 t/ha for Western Australia and 0.28 t/ha for eastern Australia. More specifically, the bias of 598 kilotons in grain production over the cropping area of 39,882 km2 in Western Australia and of 1672 kilotons in grain production over the cropping area of 59,716 km2 in eastern Australia can be decreased when using the threshold determined herein to decide the areas where the blended data can improve the prediction accuracy.

5. Discussion

Globally, wheat-growing regions are distributed within areas that experience a relatively high frequency of clouds [59]. Persistent cloud cover limits the use of HSR sensors over large spatial extents due to the low frequency of the observations, whereas the other sensors that have HTF are constrained by the LSR. Although blending improves the monitoring of rapidly changing processes such as crop growth, it may introduce unforeseen spatial and temporal variances in the blended images when images are often not observed concurrently [10], and implementing the current suite of algorithms across large areas is currently computationally expensive. Therefore, it is important to systematically quantify and evaluate the utility of blending imagery across time and space before embarking on the development of nationwide blending capabilities.
This study developed a parsimonious approach to identify when and where blending is beneficial for crop yield prediction at the 25-m pixel resolution. When incomplete Landsat series falls below 42% of the possible imagery in the growing season, blending is recommended because it improves the accuracy of the yield estimates. When incomplete Landsat series exceeds 42% of data, the use of HTF LSR data (e.g., MODIS) for the 25-m pixel-level yield prediction is recommended, reducing the computational need for blending. LTF HSR data show benefits, for example, in providing detailed information on plant photosynthesis across space; thus, they should be solely used for crop yield prediction when enough cloud-free images are available throughout the growing season.
Annual precipitation, which is strongly associated with cloudiness [60,61] and, thus, partly governs the amount of missing Landsat data, indicates which data sources should be preferably used (Figure 8). For instance, MODIS should be used for the prediction for greater than 50% of the wheatbelt during wet years (e.g., 2003, 2010, 2011, and 2016). During dry years (e.g., 2006 and 2018), the proportion of the wheatbelt where Landsat is suitable for yield prediction increases by >10% compared to the average proportion (17%). For crop yield prediction, blended data can be optimally applied across approximately 33% of the wheatbelt during dry to normal years.
Crop production fluctuates from year to year due to the rapidly changing patterns of precipitation and temperature [42,62,63]. Over the last 50 years, the amount of precipitation received by the Australian wheatbelt declined [64]. Based on model projections, it was also suggested that the changing climatic conditions will affect both the frequency and intensity of the extreme events such as floods, heatwaves, and droughts, which will impact agricultural production [65,66]. Within the context of the present study, an increase in the number of clear sky days can be beneficial for the use of RS in crop yield forecasting. Moreover, a decline in the number of rain days in recent decades within the wheatbelt area can also be noted (see Figure S4, Supplementary Materials). Here, this decline in the number of rain days is assumed to correlate with the increase in the number of days with clear skies. However, a decrease in the number of rain days does not necessarily imply an absence of clouds, as there could be non-precipitating clouds. However, studies such as Norris et al. [67], using observations and Coupled Model Intercomparison Project Phase 5 (CMIP5) model outputs, showed that, on average, there is a decline in cloud amount across the region from 60° S–60° north (N). This decline was attributed to the poleward shift of mid-latitude storm tracks, among others.
The potential influence of climate change on grain production suggests a decline in world food supply [68] and an increase in the level of exposure of the global population to the risk of hunger [69]. It is, therefore, important to ensure the accuracy and efficiency of yield prediction at anytime, anywhere, and at any scale. A more precise description of grain weight patterns in time and space provides more accurate information for precision agriculture to improve its production and sustainability. The semi-empirical carbon turn-over model used for crop yield prediction is based on historical yield data, and, in the future, relevant drivers (e.g., precipitation and temperature) and their interactions may change under climate change, thus requiring model re-calibration [4,6,70,71]. Our approach was tested with C-Crop but could be extended to other semi-empirical models [72] and models based on machine learning [73].
Development of a national-scale yield prediction system requires time series of HSR and HTF imagery to describe the crop growth; therefore, next-generation HSR and HTF satellite data like Sentinel-2 [74,75] should be tested for nationwide yield estimates post the growing season of 2015. Harmonized Landsat and Sentinel-2 surface reflectance products should be tested for national-scale crop yield prediction [76] when observed yield data for more recent years are available. However, spatio-temporal fusion of MODIS and Landsat data is still necessary for long-term studies that involve historical satellite images collected before 2015 (back to the year 2000, when MODIS was launched). Future studies should also focus on using active RS technologies, such as radio detecting and ranging (Radar) [77,78] and light detection and ranging (LiDAR) [79], for a national yield estimation because of their ability to penetrate clouds and detect a plant’s three-dimensional structural characteristics. Data blending between HSR optical imagery and active RS data (e.g., Radar and LiDAR) [80] warrants further study.

6. Conclusions

Sparse time series of satellite remote sensing, due to LTF and/or cloud contamination, represent one of the main barriers limiting accurate crop yield estimation at regional to national scales. Blending of HSR but LTF images with LSR but HTF images was proposed to increase the temporal resolution and maintain spatial details. In this study, the benefits of blending were tested for crop yield prediction across the Australian wheatbelt. We found that, when time series are gap-free, yield prediction from Landsat is the most accurate on both field and pixel scales. When Landsat time series contain <42% missing values during the growing season, blending is recommended for nationwide crop yield prediction at the 25-m pixel resolution. When Landsat time series contain ≥42% missing observations, MODIS outperforms blending. Across Australia, these recommendations would improve yield estimates by 0.15 t/ha for Western Australia and 0.28 t/ha for eastern Australia on average. By identifying where and when to blend, this work paves the way to more accurate monitoring of biophysical processes and yields, while keeping computational costs low.

Supplementary Materials

The following are available online at https://www.mdpi.com/2072-4292/12/10/1653/s1, Table S1: Summary of observed data (the number of field-years) used herein; Figure S1. Long-term (1901–2018) average monthly accumulated precipitation (mm/month) (left) and the long-term average rain days (right) across the wheatbelt for (a, b) Queensland, (c, d) New South Wales, (e, f) Victoria, (g, h) South Australia, (i, j) Western Australia, and (k, l) Tasmania. The precipitation data are sourced from Jeffrey et al. [37], and the wheat belt mask was resampled from native 2-km2 horizontal resolution onto the precipitation data grid with 5-km2 horizontal resolution using nearest neighbor [40]. The vertical black lines (a–f) represent one standard deviation of the monthly wheatbelt specific precipitation for each state. The horizontal line (g–l) represents the median of the data, the box spans from 25th to 75th quartiles of the data, and the rain day threshold is 0 mm/day. It should be noted that Northern Territory is not included in the analysis due to its small cropping area; Figure S2. An example of MODIS and Landsat blended NDVI using ESTARFM. The x-axis and y-axis are time (t, DOY) and spatial resolution (m), respectively. Both MODIS and Landsat have valid observations at t1 and t2. The image at the center of the top row is a valid observation of MODIS at ts, and that at the center of the bottom row is Landsat-like blended data at ts created using the 16-day MODIS composite images on the DOYs 257, 273, and 289, as well as the Landsat images acquired on the DOYs 257 and 289; Figure S3: The implementation flowchart of validation and identification of threshold for when to blend. The shaded areas indicate the original data sources; Figure S4: Long-term (1900–2018) average monthly accumulated precipitation (mm/month) across (a) eastern Australian, (b) Western Australia, and (c) the wheatbelt. The precipitation data are sourced from Jeffrey et al. [37].

Author Contributions

Conceptualization, Y.C., T.R.M., and R.J.D.; methodology, Y.C.; software, N.O. and N.G.; validation, Y.C.; formal analysis, Y.C.; investigation, Y.C. and F.W.; resources, L.L. and N.G.; writing—original draft preparation, Y.C.; writing—review and editing, T.R.M., R.J.D., F.W., N.G., and R.L.; visualization, Y.C. and N.G.; supervision, T.R.M. and R.J.D.; project administration, R.L.; funding acquisition, R.L. All authors read and agreed to the published version of the manuscript.

Funding

The authors acknowledged the support of the Digiscape Future Science Platform, funded by the CSIRO.

Acknowledgments

Appreciation is extended to numerous industry participants who provided training data in the form of yield maps, accessed by the project team. Randall J. Donohue and Tim R. McVicar acknowledge the support of the ARC Center of Excellence for Climate Extremes (Australian Research Council grant CE170100023). We thank the two anonymous reviewers and the Remote Sensing Academic Editor for helpful comments that helped us improve this paper.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Cohen, J.E. Human population: The next half century. Science 2003, 302, 1172–1175. [Google Scholar] [CrossRef]
  2. Jones, J.W.; Antle, J.M.; Basso, B.; Boote, K.J.; Conant, R.T.; Foster, I.; Godfray, H.C.J.; Herrero, M.; Howitt, R.E.; Janssen, S.; et al. Brief history of agricultural systems modeling. Agric. Syst. 2017, 155, 240–254. [Google Scholar] [CrossRef] [PubMed]
  3. Prasad, A.K.; Chai, L.; Singh, R.P.; Kafatos, M. Crop yield estimation model for Iowa using remote sensing and surface parameters. Int. J. Appl. Earth Obs. Geoinf. 2006, 8, 26–33. [Google Scholar] [CrossRef]
  4. Doraiswamy, P.C.; Moulin, S.; Cook, P.W.; Stern, A. Crop yield assessment from remote sensing. Photogramm. Eng. Remote Sens. 2003, 69, 665–674. [Google Scholar] [CrossRef]
  5. Serrano, L.; Filella, I.; Penuelas, J. Remote sensing of biomass and yield of winter wheat under different nitrogen supplies. Crop. Sci. 2000, 40, 723–731. [Google Scholar] [CrossRef] [Green Version]
  6. Donohue, R.J.; Lawes, R.A.; Mata, G.; Gobbett, D.; Ouzman, J. Towards a national, remote-sensing-based model for predicting field-scale crop yield. Field Crop. Res. 2018, 227, 79–90. [Google Scholar] [CrossRef]
  7. Myers, E.; Kerekes, J.; Daughtry, C.; Russ, A. Assessing the Impact of Satellite Revisit Rate on Estimation of Corn Phenological Transition Timing through Shape Model Fitting. Remote Sens. 2019, 11, 2558. [Google Scholar] [CrossRef] [Green Version]
  8. Waldner, F.; Chen, Y.; Horan, H.; Hochan, Z. High temporal resolution of leaf area data improves empirical estimation of grain yield. Sci. Rep. Press 2019, 9, 1–4. [Google Scholar] [CrossRef] [Green Version]
  9. Sakamoto, T.; Gitelson, A.A.; Arkebauer, T.J. Near real-time prediction of US corn yields based on time-series MODIS data. Remote Sens. Environ. 2014, 147, 219–231. [Google Scholar] [CrossRef]
  10. Emelyanova, I.V.; McVicar, T.R.; Van Niel, T.G.; Li, L.T.; van Dijk, A.I.J.M. Assessing the accuracy of blending Landsat–MODIS surface reflectances in two landscapes with contrasting spatial and temporal dynamics: A framework for algorithm selection. Remote Sens. Envrion. 2013, 133, 193–209. [Google Scholar] [CrossRef]
  11. Zhu, X.; Chen, J.; Gao, F.; Chen, X.; Masek, J.G. An enhanced spatial and temporal adaptive reflectance fusion model for complex heterogeneous regions. Remote Sens. Environ. 2010, 114, 2610–2623. [Google Scholar] [CrossRef]
  12. Gao, F.; Masek, J.; Schwaller, M.; Hall, F. On the blending of the Landsat and MODIS surface reflectance: Predicting daily Landsat surface reflectance. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2207–2218. [Google Scholar]
  13. ABS. Themes: Land Use on Farms, Australia, Year Ended 30 June 2017; Australian Bureau of Statistics: Canberra, Australia, 2017. Available online: http://www.abs.gov.au/ausstats/[email protected]/mf/4627.0 (accessed on 7 April 2020).
  14. Duveiller, G.; Baret, F.; Defourny, P. Crop specific green area index retrieval from MODIS data at regional scale by controlling pixel-target adequacy. Remote Sens. Environ. 2011, 115, 2686–2701. [Google Scholar] [CrossRef]
  15. Waldner, F.; Defourny, P. Where can pixel counting area estimates meet user-defined accuracy requirements? Int. J. Appl. Earth Obs. Geoinf. 2017, 60, 1–10. [Google Scholar] [CrossRef]
  16. Whitcraft, A.; Becker-Reshef, I.; Killough, B.; Justice, C. Meeting earth observation requirements for global agricultural monitoring: An evaluation of the revisit capabilities of current and planned moderate resolution optical earth observing missions. Remote Sens. 2015, 7, 1482–1503. [Google Scholar] [CrossRef] [Green Version]
  17. Lobell, D.B.; Thau, D.; Seifert, C.; Engle, E.; Little, B. A scalable satellite-based crop yield mapper. Remote Sens. Environ. 2015, 164, 324–333. [Google Scholar] [CrossRef]
  18. Schowengerdt, R.A. Remote Sensing: Models and Methods for Image Processing; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
  19. Kang, S.; Running, S.W.; Zhao, M.; Kimball, J.S.; Glassy, J. Improving continuity of MODIS terrestrial photosynthesis products using an interpolation scheme for cloudy pixels. Int. J. Remote Sens. 2005, 26, 1659–1676. [Google Scholar] [CrossRef]
  20. Poggio, L.; Gimona, A.; Brown, I. Spatio-temporal MODIS EVI gap filling under cloud cover: An example in Scotland. ISPRS J. Photogramm. Remote Sens. 2012, 72, 56–72. [Google Scholar] [CrossRef]
  21. Borak, J.S.; Jasinski, M.F. Effective interpolation of incomplete satellite-derived leaf-area index time series for the continental United States. Agric. For. Meteorol. 2009, 149, 320–332. [Google Scholar] [CrossRef] [Green Version]
  22. Jarihani, A.; McVicar, T.; Van Niel, T.; Emelyanova, I.; Callow, J.; Johansen, K. Blending Landsat and MODIS data to generate multispectral indices: A comparison of “Index-then-Blend” and “Blend-then-Index” approaches. Remote Sens. 2014, 6, 9213–9238. [Google Scholar] [CrossRef] [Green Version]
  23. Zhang, J. Multi-source remote sensing data fusion: Status and trends. Int. J. Image Data Fusion 2010, 1, 5–24. [Google Scholar] [CrossRef] [Green Version]
  24. Pohl, C.; Van Genderen, J.L. Review article multisensor image fusion in remote sensing: Concepts, methods and applications. Int. J. Remote Sens. 1998, 19, 823–854. [Google Scholar] [CrossRef] [Green Version]
  25. Viovy, N.; Arino, O.; Belward, A. The Best Index Slope Extraction (BISE): A method for reducing noise in NDVI time-series. Int. J. Remote Sens. 1992, 13, 1585–1590. [Google Scholar] [CrossRef]
  26. Löw, F.; Biradar, C.; Dubovyk, O.; Fliemann, E.; Akramkhanov, A.; Narvaez Vallejo, A.; Waldner, F. Regional-scale monitoring of cropland intensity and productivity with multi-source satellite image time series. GIsci. Remote Sens. 2018, 55, 539–567. [Google Scholar] [CrossRef]
  27. Dong, T.; Liu, J.; Qian, B.; Zhao, T.; Jing, Q.; Geng, X.; Wang, J.; Huffman, T.; Shang, J. Estimating winter wheat biomass by assimilating leaf area index derived from fusion of Landsat-8 and MODIS data. Int. J. Appl. Earth Obs. Geoinf. 2016, 49, 63–74. [Google Scholar] [CrossRef]
  28. Meng, J.; Du, X.; Wu, B. Generation of high spatial and temporal resolution NDVI and its application in crop biomass estimation. Int. J. Digit. Earth 2013, 6, 203–218. [Google Scholar] [CrossRef]
  29. Wang, L.; Tian, Y.; Yao, X.; Zhu, Y.; Cao, W. Predicting grain yield and protein content in wheat by fusing multi-sensor and multi-temporal remote-sensing images. Field Crop. Res. 2014, 164, 178–188. [Google Scholar] [CrossRef]
  30. Gao, F.; Anderson, M.C.; Zhang, X.; Yang, Z.; Alfieri, J.G.; Kustas, W.P.; Mueller, R.; Johnson, D.M.; Prueger, J.H. Toward mapping crop progress at field scales through fusion of Landsat and MODIS imagery. Remote Sens. Environ. 2017, 188, 9–25. [Google Scholar] [CrossRef] [Green Version]
  31. Semmens, K.A.; Anderson, M.C.; Kustas, W.P.; Gao, F.; Alfieri, J.G.; McKee, L.; Prueger, J.H.; Hain, C.R.; Cammalleri, C.; Yang, Y. Monitoring daily evapotranspiration over two California vineyards using Landsat 8 in a multi-sensor data fusion approach. Remote Sens. Environ. 2016, 185, 155–170. [Google Scholar] [CrossRef] [Green Version]
  32. Yang, Y.; Anderson, M.C.; Gao, F.; Wardlow, B.; Hain, C.R.; Otkin, J.A.; Alfieri, J.; Yang, Y.; Sun, L.; Dulaney, W. Field-scale mapping of evaporative stress indicators of crop yield: An application over Mead, NE, USA. Remote Sens. Environ. 2018, 210, 387–402. [Google Scholar] [CrossRef]
  33. Gao, F.; Anderson, M.; Daughtry, C.; Johnson, D. Assessing the variability of corn and soybean yields in central Iowa using high spatiotemporal resolution multi-satellite imagery. Remote Sens. 2018, 10, 1489. [Google Scholar] [CrossRef] [Green Version]
  34. He, M.; Kimball, J.; Maneta, M.; Maxwell, B.; Moreno, A.; Beguería, S.; Wu, X. Regional crop gross primary productivity and yield estimation using fused landsat-MODIS data. Remote Sens. 2018, 10, 372. [Google Scholar] [CrossRef] [Green Version]
  35. Liao, C.; Wang, J.; Dong, T.; Shang, J.; Liu, J.; Song, Y. Using spatio-temporal fusion of Landsat-8 and MODIS data to derive phenology, biomass and yield estimates for corn and soybean. Sci. Total Environ. 2019, 650, 1707–1721. [Google Scholar] [CrossRef] [PubMed]
  36. Holper, P.N. Climate Change, Science Information Paper: Australian Rainfall—Past, Present and Future; CSIRO: Canberra, Australia, 2011. [Google Scholar]
  37. Jeffrey, S.J.; Carter, J.O.; Moodie, K.B.; Beswick, A.R. Using spatial interpolation to construct a comprehensive archive of Australian climate data. Environ. Model. Softw. 2001, 16, 309–330. [Google Scholar] [CrossRef]
  38. Li, F.; Jupp, D.L.; Reddy, S.; Lymburner, L.; Mueller, N.; Tan, P.; Islam, A. An evaluation of the use of atmospheric and BRDF correction to standardize Landsat data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2010, 3, 257–270. [Google Scholar] [CrossRef]
  39. Rouse, J.W., Jr.; Haas, R.; Schell, J.; Deering, D. Monitoring Vegetation Systems in the Great Plains with ERTS; NASA: Washington, DC, USA, 1974.
  40. Sibson, R. A brief description of natural neighbour interpolation. In Interpreting Multivariate Data; John Wiley & Sons: New York, NY, USA, 1981; pp. 21–36. [Google Scholar]
  41. Cockram, J.; Jones, H.; Leigh, F.J.; O’Sullivan, D.; Powell, W.; Laurie, D.A.; Greenland, A.J. Control of flowering time in temperate cereals: Genes, domestication, and sustainable productivity. J. Exp. Bot. 2007, 58, 1231–1244. [Google Scholar] [CrossRef] [PubMed]
  42. Hochman, Z.; Gobbett, D.L.; Horan, H. Climate trends account for stalled wheat yields in Australia since 1990. Glob. Chang. Biol. 2017, 23, 2071–2081. [Google Scholar] [CrossRef]
  43. Emelyanova, I.V.; McVicar, T.R.; Van Niel, T.G.; Li, L.T.; Van Dijk, A.I.J.M. On blending Landsat-MODIS surface reflectances in two landscapes with contrasting spectral, spatial and temporal dynamics. In WIRADA Project 3.4: Technical Report; CSIRO: Water for a Healthy Country Flagship: Canberra, Australia, 2012; p. 72. Available online: https://publications.csiro.au/rpr/pub?list=SEA&pid=csiro:EP128838 (accessed on 7 April 2020).
  44. Bramley, R.; Williams, S. A Protocol for the Construction of Yield Maps from Data Collected Using Commercially Available Grape Yield Monitors; Cooperative Research Centre for Viticulture: Adelaide, Australia, 2001.
  45. Kira, T. Primary production of forests. In Photosynthesis and Productivity in Different Environments; Cambridge University Press: Cambridge, UK, 1975. [Google Scholar]
  46. Sitch, S.; Smith, B.; Prentice, I.C.; Arneth, A.; Bondeau, A.; Cramer, W.; Kaplan, J.; Levis, S.; Lucht, W.; Sykes, M.T. Evaluation of ecosystem dynamics, plant geography and terrestrial carbon cycling in the LPJ dynamic global vegetation model. Glob. Chang. Biol. 2003, 9, 161–185. [Google Scholar] [CrossRef]
  47. McCree, K.J. Test of current definitions of photosynthetically active radiation against leaf photosynthesis data. Agric. Meteorol. 1972, 10, 443–453. [Google Scholar] [CrossRef]
  48. Roderick, M.L. Estimating the diffuse component from daily and monthly measurements of global radiation. Agric. For. Meteorol. 1999, 95, 169–185. [Google Scholar] [CrossRef]
  49. Iqbal, M. An Introduction to Solar Radiation; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
  50. Bristow, K.L.; Campbell, G.S. On the relationship between incoming solar radiation and daily maximum and minimum temperature. Agric. For. Meteorol. 1984, 31, 159–166. [Google Scholar] [CrossRef]
  51. McVicar, T.R.; Jupp, D.L. Estimating one-time-of-day meteorological data from standard daily data as inputs to thermal remote sensing based energy balance models. Agric. For. Meteorol. 1999, 96, 219–238. [Google Scholar] [CrossRef]
  52. Wilson, J.P.; Gallant, J.C. Terrain analysis: Principles and Applications; John Wiley & Sons: New York, NY, USA, 2000. [Google Scholar]
  53. Verger, A.; Baret, F.; Camacho, F. Optimal modalities for radiative transfer-neural network estimation of canopy biophysical characteristics: Evaluation over an agricultural area with CHRIS/PROBA observations. Remote Sens. Environ. 2011, 115, 415–426. [Google Scholar] [CrossRef]
  54. Li, W.; Weiss, M.; Waldner, F.; Defourny, P.; Demarez, V.; Morin, D.; Hagolle, O.; Baret, F. A generic algorithm to estimate LAI, FAPAR and FCOVER variables from SPOT4_HRVIR and Landsat sensors: Evaluation of the consistency and comparison with ground measurements. Remote Sens. 2015, 7, 15494–15516. [Google Scholar] [CrossRef] [Green Version]
  55. Donohue, R.J.; Hume, I.; Roderick, M.; McVicar, T.R.; Beringer, J.; Hutley, L.; Gallant, J.C.; Austin, J.; van Gorsel, E.; Cleverly, J. Evaluation of the remote-sensing-based DIFFUSE model for estimating photosynthesis of vegetation. Remote Sens. Environ. 2014, 155, 349–365. [Google Scholar] [CrossRef]
  56. Tambussi, E.; Nogues, S.; Ferrio, P.; Voltas, J.; Araus, J. Does higher yield potential improve barley performance in Mediterranean conditions? A case study. Field Crop. Res. 2005, 91, 149–160. [Google Scholar] [CrossRef]
  57. Jensen, C.; Mogensen, V.; Mortensen, G.; Andersen, M.N.; Schjoerring, J.; Thage, J.; Koribidis, J. Leaf photosynthesis and drought adaptation in field-grown oilseed rape (Brassica napus L.). Funct. Plant. Biol. 1996, 23, 631–644. [Google Scholar] [CrossRef]
  58. ABARES. Australian Agricultural Overview; Australian Bureau of Agricultural and Resource Economics and Sciences: Canberra, Australia, 2018; p. 26.
  59. Wilson, A.M.; Jetz, W. Remotely sensed high-resolution global cloud dynamics for predicting ecosystem and biodiversity distributions. PLoS Biol. 2016, 14, e1002415. [Google Scholar] [CrossRef]
  60. Jovanovic, B.; Collins, D.; Braganza, K.; Jakob, D.; Jones, D.A. A high-quality monthly total cloud amount dataset for Australia. Clim. Chang. 2011, 108, 485–517. [Google Scholar] [CrossRef]
  61. Portmann, R.W.; Solomon, S.; Hegerl, G.C. Spatial and seasonal patterns in climate change, temperatures, and precipitation across the United States. Proc. Natl. Acad. Sci. USA 2009, 106, 7324–7329. [Google Scholar] [CrossRef] [Green Version]
  62. Ludwig, F.; Milroy, S.P.; Asseng, S. Impacts of recent climate change on wheat production systems in Western Australia. Clim. Chang. 2009, 92, 495–517. [Google Scholar] [CrossRef] [Green Version]
  63. Dreccer, M.F.; Fainges, J.; Whish, J.; Ogbonnaya, F.C.; Sadras, V.O. Comparison of sensitive stages of wheat, barley, canola, chickpea and field pea to temperature and water stress across Australia. Agric. For. Meteorol. 2018, 248, 275–294. [Google Scholar] [CrossRef]
  64. Cai, W.; Cowan, T. Dynamics of late autumn rainfall reduction over southeastern Australia. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
  65. Van Dijk, A.I.; Beck, H.E.; Crosbie, R.S.; de Jeu, R.A.; Liu, Y.Y.; Podger, G.M.; Timbal, B.; Viney, N.R. The millennium drought in southeast Australia (2001–2009): Natural and human causes and implications for water resources, ecosystems, economy, and society. Water Resour. Res. 2013, 49, 1040–1057. [Google Scholar] [CrossRef]
  66. Kiem, A.S.; Johnson, F.; Westra, S.; van Dijk, A.; Evans, J.P.; O’Donnell, A.; Rouillard, A.; Barr, C.; Tyler, J.; Thyer, M. Natural hazards in Australia: Droughts. Clim. Chang. 2016, 139, 37–54. [Google Scholar] [CrossRef]
  67. Norris, J.R.; Allen, R.J.; Evan, A.T.; Zelinka, M.D.; O’Dell, C.W.; Klein, S.A. Evidence for climate change in the satellite cloud record. Nature 2016, 536, 72. [Google Scholar] [CrossRef] [Green Version]
  68. Rosenzweig, C.; Parry, M.L. Potential impact of climate change on world food supply. Nature 1994, 367, 133–138. [Google Scholar] [CrossRef]
  69. Parry, M.L.; Rosenzweig, C.; Iglesias, A.; Livermore, M.; Fischer, G. Effects of climate change on global food production under SRES emissions and socio-economic scenarios. Glob. Environ. Chang. 2004, 14, 53–67. [Google Scholar] [CrossRef]
  70. Doraiswamy, P.; Hatfield, J.; Jackson, T.; Akhmedov, B.; Prueger, J.; Stern, A. Crop condition and yield simulations using Landsat and MODIS. Remote Sens. Environ. 2004, 92, 548–559. [Google Scholar] [CrossRef]
  71. Ferencz, C.; Bognar, P.; Lichtenberger, J.; Hamar, D.; Tarcsai, G.; Timar, G.; Molnar, G.; Pásztor, S.; Steinbach, P.; Szekely, B. Crop yield estimation by satellite remote sensing. Int. J. Remote Sens. 2004, 25, 4113–4149. [Google Scholar] [CrossRef]
  72. Chen, Y.; Donohue, R.J.; McVicar, T.R.; Waldner, F.; Mata, G.; Ota, N.; Houshmandfar, A.; Dayal, K.; Lawes, R.A. Nationwide crop yield estimation based on photosynthesis and meteorological stress indices. Agric. For. Meteorol. 2020, 284, 107872. [Google Scholar] [CrossRef]
  73. Kamir, E.; Waldner, F.; Hochman, Z. Estimating wheat yields in Australia using climate records, satellite image time series and machine learning methods. ISPRS J. Photogramm. Remote Sens. 2020, 160, 124–135. [Google Scholar] [CrossRef]
  74. Battude, M.; Al Bitar, A.; Morin, D.; Cros, J.; Huc, M.; Sicre, C.M.; Le Dantec, V.; Demarez, V. Estimating maize biomass and yield over large areas using high spatial and temporal resolution Sentinel-2 like remote sensing data. Remote Sens. Environ. 2016, 184, 668–681. [Google Scholar] [CrossRef]
  75. Skakun, S.; Vermote, E.; Roger, J.-C.; Franch, B. Combined use of Landsat-8 and Sentinel-2A images for winter crop mapping and winter wheat yield assessment at regional scale. AIMS Geosci. 2017, 3, 163. [Google Scholar] [CrossRef]
  76. Skakun, S.; Vermote, E.; Franch, B.; Roger, J.-C.; Kussul, N.; Ju, J.; Masek, J. Winter Wheat Yield Assessment from Landsat 8 and Sentinel-2 Data: Incorporating Surface Reflectance, Through Phenological Fitting, into Regression Yield Models. Remote Sens. 2019, 11, 1768. [Google Scholar] [CrossRef] [Green Version]
  77. Betbeder, J.; Fieuzal, R.; Baup, F. Assimilation of LAI and dry biomass data from optical and SAR images into an agro-meteorological model to estimate soybean yield. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 2540–2553. [Google Scholar] [CrossRef]
  78. Patel, P.; Srivastava, H.S.; Navalgund, R.R. Estimating wheat yield: An approach for estimating number of grains using cross-polarised ENVISAT-1 ASAR data. In Proceedings of the Microwave Remote Sensing of the Atmosphere and Environment V, Goa, India, 13–17 November 2006; p. 641009. [Google Scholar]
  79. Eitel, J.U.; Magney, T.S.; Vierling, L.A.; Brown, T.T.; Huggins, D.R. LiDAR based biomass and crop nitrogen estimates for rapid, non-destructive assessment of wheat nitrogen status. Field Crop. Res. 2014, 159, 21–32. [Google Scholar] [CrossRef]
  80. Joshi, N.; Baumann, M.; Ehammer, A.; Fensholt, R.; Grogan, K.; Hostert, P.; Jepsen, M.; Kuemmerle, T.; Meyfroidt, P.; Mitchard, E. A review of the application of optical and radar remote sensing data fusion to land use mapping and monitoring. Remote Sens. 2016, 8, 70. [Google Scholar] [CrossRef] [Green Version]
Remotesensing 12 01653 g001 550
Figure 1. Study sites and the crop growing season (April–October) average accumulated precipitation (mm for the years 2009–2015) across the Australian wheatbelt (~53 million ha) [13]. The precipitation data are sourced from Jeffrey et al. [37].
Figure 1. Study sites and the crop growing season (April–October) average accumulated precipitation (mm for the years 2009–2015) across the Australian wheatbelt (~53 million ha) [13]. The precipitation data are sourced from Jeffrey et al. [37].
Remotesensing 12 01653 g001
Remotesensing 12 01653 g002 550
Figure 2. Box–whisker plots of 1901 to 2018 averaged (a) monthly accumulated precipitation (mm/month) across the Australian wheatbelt (see Figure 1) and (b) monthly probability of rain days (bottom). For both parts, the horizontal line represents the median of the data, the box spans from 25th to 75th quartiles of the data, and the circles past the end of the whiskers are outliers, while the rain day threshold is 0 mm/day.
Figure 2. Box–whisker plots of 1901 to 2018 averaged (a) monthly accumulated precipitation (mm/month) across the Australian wheatbelt (see Figure 1) and (b) monthly probability of rain days (bottom). For both parts, the horizontal line represents the median of the data, the box spans from 25th to 75th quartiles of the data, and the circles past the end of the whiskers are outliers, while the rain day threshold is 0 mm/day.
Remotesensing 12 01653 g002
Remotesensing 12 01653 g003 550
Figure 3. The quantile of Landsat missing pixels in the fields for which observed yield data are available (2009 to 2015).
Figure 3. The quantile of Landsat missing pixels in the fields for which observed yield data are available (2009 to 2015).
Remotesensing 12 01653 g003
Remotesensing 12 01653 g004 550
Figure 4. Validation of C-Crop-predicted yield pooled for wheat, barley, and canola using Landsat, MODIS, and L–M blended data where the complete Landsat time series are observed (the fraction of missing Landsat series = 0). From top to bottom, the first (a–c), second (d–f), and third (g–i) rows show the comparison between observed (x-axis) and model-predicted yields (y-axis) on the field scale (n = 139), 250-m pixel level (n = 2367), and 25-m pixel level (n = 113,329), respectively, where n is the sample size. From left to right, the first (a,d,g), second (b,e,h), and third (c,f,i) columns delineate the validation using Landsat, MODIS, and L–M blended data, respectively. The solid black line is the line of best fit, the purple and the yellow lines represent the upper and lower bounds of the prediction confidence intervals (i.e., p = 0.01 and p = 0.05), and the black dashed line is the 1:1 line.
Figure 4. Validation of C-Crop-predicted yield pooled for wheat, barley, and canola using Landsat, MODIS, and L–M blended data where the complete Landsat time series are observed (the fraction of missing Landsat series = 0). From top to bottom, the first (a–c), second (d–f), and third (g–i) rows show the comparison between observed (x-axis) and model-predicted yields (y-axis) on the field scale (n = 139), 250-m pixel level (n = 2367), and 25-m pixel level (n = 113,329), respectively, where n is the sample size. From left to right, the first (a,d,g), second (b,e,h), and third (c,f,i) columns delineate the validation using Landsat, MODIS, and L–M blended data, respectively. The solid black line is the line of best fit, the purple and the yellow lines represent the upper and lower bounds of the prediction confidence intervals (i.e., p = 0.01 and p = 0.05), and the black dashed line is the 1:1 line.
Remotesensing 12 01653 g004
Remotesensing 12 01653 g005 550
Figure 5. Validation of C-Crop-predicted yield pooled for wheat, barley, and canola using MODIS and L–M blended data when the complete Landsat time series are not available (the fraction of missing Landsat series ≥0.083). From top to bottom, the first (a,b), second (c,d), and third (e,f) rows show the comparison between observed (x-axis) and model-predicted yields (y-axis) on the field scale (n = 210), 250-m pixel level (n = 3978), and 25-m pixel level (n = 231,667), respectively, where n is the sample size. From left to right, the first (a,c,e) and second (b,d,f) columns delineate the validation using MODIS and L–M blended data, respectively. The solid black line is the line of best fit, the purple and the yellow lines represent the upper and lower bounds of the prediction confidence intervals (i.e., p = 0.01 and p = 0.05), and the black dashed line is the 1:1 line.
Figure 5. Validation of C-Crop-predicted yield pooled for wheat, barley, and canola using MODIS and L–M blended data when the complete Landsat time series are not available (the fraction of missing Landsat series ≥0.083). From top to bottom, the first (a,b), second (c,d), and third (e,f) rows show the comparison between observed (x-axis) and model-predicted yields (y-axis) on the field scale (n = 210), 250-m pixel level (n = 3978), and 25-m pixel level (n = 231,667), respectively, where n is the sample size. From left to right, the first (a,c,e) and second (b,d,f) columns delineate the validation using MODIS and L–M blended data, respectively. The solid black line is the line of best fit, the purple and the yellow lines represent the upper and lower bounds of the prediction confidence intervals (i.e., p = 0.01 and p = 0.05), and the black dashed line is the 1:1 line.
Remotesensing 12 01653 g005
Remotesensing 12 01653 g006 550
Figure 6. The statistical analysis of missing data in Landsat for 25-m pixel-level yield prediction, by evaluating (a) R2 and (b) RMSE against the fraction of Landsat missing data during the growing season. L–M blended data were used to fill the gaps (LLM) in the incomplete Landsat series.
Figure 6. The statistical analysis of missing data in Landsat for 25-m pixel-level yield prediction, by evaluating (a) R2 and (b) RMSE against the fraction of Landsat missing data during the growing season. L–M blended data were used to fill the gaps (LLM) in the incomplete Landsat series.
Remotesensing 12 01653 g006
Remotesensing 12 01653 g007 550
Figure 7. Multi-sensor optimal data selection across the wheatbelt (2000–2018) for 25-m pixel-level crop yield prediction, using the probability of MODIS, Landsat, and LLM images. Blue denotes regions where incomplete Landsat series have a fraction of missing data exceeding 42%, thus indicating where MODIS should be used for yield estimates because it provides more frequent observations than Landsat. Green areas show where adjacent Landsat orbits overlap and, thus, where a complete once every 16-day Landsat series over the whole growing season is available. Areas colored red are those where the fraction of Landsat missing data is below the 0.42 threshold identified previously in Figure 6 when L–M blended data improve the yield prediction accuracy.
Figure 7. Multi-sensor optimal data selection across the wheatbelt (2000–2018) for 25-m pixel-level crop yield prediction, using the probability of MODIS, Landsat, and LLM images. Blue denotes regions where incomplete Landsat series have a fraction of missing data exceeding 42%, thus indicating where MODIS should be used for yield estimates because it provides more frequent observations than Landsat. Green areas show where adjacent Landsat orbits overlap and, thus, where a complete once every 16-day Landsat series over the whole growing season is available. Areas colored red are those where the fraction of Landsat missing data is below the 0.42 threshold identified previously in Figure 6 when L–M blended data improve the yield prediction accuracy.
Remotesensing 12 01653 g007
Remotesensing 12 01653 g008 550
Figure 8. Yearly analysis of multi-sensor data selection for 25-m pixel-level crop yield prediction (2000–2018) by evaluating (a) the area percentage and (b) its correlation with the annual precipitation (mm/year). The white dashed line shows that the area percentage is 50. µ: mean of population values; σ: standard deviation; r: correlation coefficient. The symbols in (b) are labeled with the last two digits of the year.
Figure 8. Yearly analysis of multi-sensor data selection for 25-m pixel-level crop yield prediction (2000–2018) by evaluating (a) the area percentage and (b) its correlation with the annual precipitation (mm/year). The white dashed line shows that the area percentage is 50. µ: mean of population values; σ: standard deviation; r: correlation coefficient. The symbols in (b) are labeled with the last two digits of the year.
Remotesensing 12 01653 g008
Remotesensing 12 01653 g009 550
Figure 9. Scattergram for C-Crop-predicted yield against observed values for 2015 at the field level for (a) Western Australia (n = 63) and (b) eastern Australia (n = 6) wheatbelt using MODIS and L–M blended data for gap-filling Landsat (LLM) when the fraction of incomplete Landsat series is below 42% for the growing season. The RMSE statistics have units of t/ha.
Figure 9. Scattergram for C-Crop-predicted yield against observed values for 2015 at the field level for (a) Western Australia (n = 63) and (b) eastern Australia (n = 6) wheatbelt using MODIS and L–M blended data for gap-filling Landsat (LLM) when the fraction of incomplete Landsat series is below 42% for the growing season. The RMSE statistics have units of t/ha.
Remotesensing 12 01653 g009
Table
Table 1. Review of studies that used data fusion approaches to estimate crop yields and other variables highly related to crop yield (e.g., growing season evapotranspiration and crop phenology). Records are sorted chronologically then alphabetically. When more than one site is reported in a single paper, these are identified with an (A) and (B) in the relevant columns as required. R2: the coefficient of determination; RMSE: root-mean-square error; MAE: mean absolute error; RMAE: relative MAE; NR: not reported. In Australia, dryland agriculture is practiced across the region known colloquially as the “wheatbelt”. STARFM—Spatial and Temporal Adaptive Reflectance Fusion Model; ESTARFM—enhanced STARFM; MODIS—Moderate Resolution Imaging Spectroradiometer; NIR—near infrared; US—United States; NE—New England; NASA—National Aeronautics and Space Administration; L–M—Landsat/MODIS blend; HTF—high temporal frequency; HSR—high spatial resolution.
Table 1. Review of studies that used data fusion approaches to estimate crop yields and other variables highly related to crop yield (e.g., growing season evapotranspiration and crop phenology). Records are sorted chronologically then alphabetically. When more than one site is reported in a single paper, these are identified with an (A) and (B) in the relevant columns as required. R2: the coefficient of determination; RMSE: root-mean-square error; MAE: mean absolute error; RMAE: relative MAE; NR: not reported. In Australia, dryland agriculture is practiced across the region known colloquially as the “wheatbelt”. STARFM—Spatial and Temporal Adaptive Reflectance Fusion Model; ESTARFM—enhanced STARFM; MODIS—Moderate Resolution Imaging Spectroradiometer; NIR—near infrared; US—United States; NE—New England; NASA—National Aeronautics and Space Administration; L–M—Landsat/MODIS blend; HTF—high temporal frequency; HSR—high spatial resolution.
ReferenceBlending AlgorithmRemote Sensing (RS) DataCrop TypeRS Variables (e.g., Vegetation Index (VI))/Study Period/Region/Study Area (km2)RS-Bases Model to Estimate Crop YieldsKey Results and Accuracy
[28]Spatial and Temporal Adaptive Vegetation Index Fusion Model (STAVIF)MODIS and Huanjing Satellite Charge-Coupled Device (HJ-CCD)Winter wheatNormalized difference vegetation index (NDVI)/2008–2009/Yucheng, Shandong, China/NREmpirical modelThe estimated winter wheat biomass correlated well with observed biomass (R2 = 0.88 and MAE = 17.2 kg/ha) using the blended data.
[29]STARFMSatellite for Observation of Earth (SPOT) 5 and HJ-1 CCDWinter wheatNDVI and ratio vegetation index (RVI) (NIR/Red)/2008–2009/(A) Rugao county, Jiangsu, and (B) Anyang county, Henan, China/(A) 0.36 km2 and (B) 0.30 km2Empirical model(A) The accumulated NDVI derived from the blended data gave a higher prediction accuracy (R2 = 0.67 and RMSE = 0.36 t/ha) for wheat yield at Rugao.
(B) The accumulated RVI derived from the blended data produced a higher prediction accuracy (R2 = 0.65 and RMSE = 0.36 t/ha) for wheat yield at Anyang.
[31]STARFMMODIS and LandsatCorn and soybeanEvapotranspiration (ET)/2013/Central Valley, California, the US/(A) 0.34 km2 and (B) 0.21 km2Empirical modelThe daily ET derived from the blended data produced the RMAE of 19% with the observed ET (mm/day). The spatial pattern of cumulative ET corresponded to the measured yield.
[27]ESTARFMMODIS and LandsatWinter wheatGreen leaf area index (GLAI)/2013/Southwestern Ontario, Canada/225 km2Semi-empirical modelThe Landsat GLAI (GLAIL) produced an R2 of 0.77 and RMSE of 2.31 t/ha; the blended GLAI (GLAIF) resulted in an R2 of 0.71 and RMSE of 1.93 t/ha; the combination of GLAIL and GLAIF led to further improvements (R2 = 0.76 and RMSE = 1.76 t/ha).
[30]ESTARFMMODIS and LandsatCorn and soybeanNDVI/2001–2014/Central Iowa, the US/200 km2Empirical modelA linear correlation (R2 = 0.83) between remotely sensed green-up dates and the emergence dates reported by NASA.
[32]STARFMMODIS and LandsatMaizeET/2010–2014/Mead, NE, the US/(A) 0.49 km2, (B) 0.52 km2, and (C) 0.65 km2Empirical modelThe county-level correlation between observed and predicted maize yields improved from 0.47 to 0.93 when aligning the ratio of actual-to-reference ET by emergence date rather than calendar date.
[33]STARFMMODIS and LandsatCorn and soybeanNDVI and enhanced vegetation index (EVI2)/2001–2015/Central Iowa, the US/200 km2Empirical modelMaximum EVI2 derived from L–M blended data produced the highest R2 (0.59 and 0.39) and the lowest RMAE (6.1% and 9.1%) for corn and soybeans, respectively, compared with using single data source alone.
[34]A pixel-wise linear regression modelMODIS and LandsatAlfalfa, barley, maize, peas, durum wheat, spring wheat, and winter wheatNDVI/2008–2015/Montana, the US/4.13 million haSemi-empirical modelA correlation of 0.96 (R2 = 0.92, relative RMSE = 37.0%, p < 0.05) resulted when comparing the yield prediction using the blended data with the reported crop production data on county level.
[26]ESTARFMMODIS and LandsatCotton and winter wheatNDVI/2004–2014/Fergana Valley, Uzbekistan/NRSemi-empirical modelThe R2 is 0.56 (RMSE = 0.63 t/ha) for wheat, and 0.631(RMSE = 0.48 t/ha) for cotton, respectively.
[35]STARFMMODIS and LandsatCorn and soybeanGLAI/2015/Southwestern Ontario, Canada/112 km2Semi-empirical modelThe RMSE of yield prediction is 1.46 t/ha (R2 = 0.56) for corn and 0.86 t/ha (R2 = 0.54) for soybean using the blended data.
This studyESTARFMMODIS and LandsatWheat, barley, and canolaNDVI/2009–2015/Australian wheatbelt/~53 million haSemi-empirical modelComparing HTF, HSR data against the blended data for yield prediction at various scales. Identifying a threshold to determine when and where the blended data can improve in the nationwide yield prediction at the 25-m pixel resolution when using multiple spatio-temporal resolution images. Quantifying and evaluating the improvements in the yield prediction accuracy at various scales based on the threshold.

Share and Cite

MDPI and ACS Style

Chen, Y.; McVicar, T.R.; Donohue, R.J.; Garg, N.; Waldner, F.; Ota, N.; Li, L.; Lawes, R. To Blend or Not to Blend? A Framework for Nationwide Landsat–MODIS Data Selection for Crop Yield Prediction. Remote Sens. 2020, 12, 1653. https://doi.org/10.3390/rs12101653

AMA Style

Chen Y, McVicar TR, Donohue RJ, Garg N, Waldner F, Ota N, Li L, Lawes R. To Blend or Not to Blend? A Framework for Nationwide Landsat–MODIS Data Selection for Crop Yield Prediction. Remote Sensing. 2020; 12(10):1653. https://doi.org/10.3390/rs12101653

Chicago/Turabian Style

Chen, Yang, Tim R. McVicar, Randall J. Donohue, Nikhil Garg, François Waldner, Noboru Ota, Lingtao Li, and Roger Lawes. 2020. "To Blend or Not to Blend? A Framework for Nationwide Landsat–MODIS Data Selection for Crop Yield Prediction" Remote Sensing 12, no. 10: 1653. https://doi.org/10.3390/rs12101653

APA Style

Chen, Y., McVicar, T. R., Donohue, R. J., Garg, N., Waldner, F., Ota, N., Li, L., & Lawes, R. (2020). To Blend or Not to Blend? A Framework for Nationwide Landsat–MODIS Data Selection for Crop Yield Prediction. Remote Sensing, 12(10), 1653. https://doi.org/10.3390/rs12101653

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop