Estimation of Hourly near Surface Air Temperature Across Israel Using an Ensemble Model
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area, Climate, and Meteorological Data
2.2. Remotely Sensed Surface Skin Temperature
2.3. ERA5 Reanalysis Data
2.4. Geospatial Variables
2.5. Statistical Methods
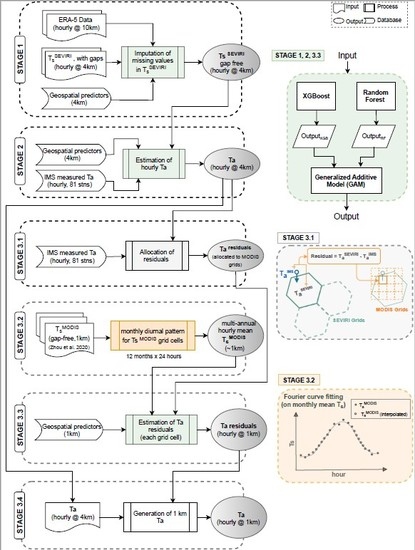
2.5.1. Stage 1 Model: Imputation of SEVIRI Ts
2.5.2. Stage 2 Model: Imputation of Ta from Ts
2.5.3. Stage 3 Model: Downscaling to 1 km Ta by Estimating Residuals
2.5.4. Tuning of Hyper Parameters and Evaluation of Model Performance
3. Results
3.1. SEVIRI Data Coverage
3.2. Performance of the Stage 1 Model
3.2.1. Feature Importance of RF and XGBoost Models in Stage 1
3.2.2. Overall, Temporal, and Spatial Performance
3.2.3. Spatial Pattern of Performance
3.2.4. Spatial Pattern of Imputed Ts of the Stage 1 Model
3.3. Performance of the Stage 2 Model
3.3.1. Feature Importance and Model Performance in Stage 2
3.3.2. Spatio-Temporal Pattern of Ta Estimated from the Stage 2 Models
3.4. Performance of the Stage 3 Model
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Johnson, N.C.; Xie, S.P.; Kosaka, Y.; Li, X. Increasing occurrence of cold and warm extremes during the recent global warming slowdown. Nat. Commun. 2018, 9, 4–6. [Google Scholar] [CrossRef] [Green Version]
- Horton, D.E.; Johnson, N.C.; Singh, D.; Swain, D.L.; Rajaratnam, B.; Diffenbaugh, N.S. Contribution of changes in atmospheric circulation patterns to extreme temperature trends. Nature 2015, 522, 465–469. [Google Scholar] [CrossRef] [Green Version]
- Coumou, D.; Robinson, A. Historic and future increase in the global land area affected by monthly heat extremes. Environ. Res. Lett. 2013, 8, 034018. [Google Scholar] [CrossRef]
- Rahmstorf, S.; Coumou, D. Increase of extreme events in a warming world. Proc. Natl. Acad. Sci. USA 2011, 108, 17905–17909. [Google Scholar] [CrossRef] [Green Version]
- Gasparrini, A.; Guo, Y.; Hashizume, M.; Lavigne, E.; Zanobetti, A.; Schwartz, J.; Tobias, A.; Tong, S.; Rocklöv, J.; Forsberg, B.; et al. Mortality risk attributable to high and low ambient temperature: A multicountry observational study. Lancet 2015, 386, 369–375. [Google Scholar] [CrossRef]
- Wang, Y.; Shi, L.; Zanobetti, A.; Schwartz, J.D. Estimating and projecting the effect of cold waves on mortality in 209 US cities. Environ. Int. 2016, 94, 141–149. [Google Scholar] [CrossRef] [Green Version]
- Huang, C.; Barnett, A.G.; Wang, X.; Vaneckova, P.; FitzGerald, G.; Tong, S. Projecting Future Heat-Related Mortality under Climate Change Scenarios: A Systematic Review. Environ. Health Perspect. 2011, 119, 1681–1690. [Google Scholar] [CrossRef] [Green Version]
- Kloog, I.; Melly, S.J.; Coull, B.A.; Nordio, F.; Schwartz, J.D. Using satellite-based spatiotemporal resolved air temperature exposure to study the association between ambient air temperature and birth outcomes in Massachusetts. Environ. Health Perspect. 2015, 123, 1053–1058. [Google Scholar] [CrossRef] [Green Version]
- Arnfield, A.J. Two decades of urban climate research: A review of turbulence, exchanges of energy and water, and the urban heat island. Int. J. Climatol. 2003, 23, 1–26. [Google Scholar] [CrossRef]
- Oke, T.R.; Mills, G.; Christen, A.; Voogt, J.A. Urban Climates; Cambridge University Press: Cambridge, UK, 2017; ISBN 9781139016476. [Google Scholar]
- Erell, E.; Pearlmutter, D.; Williamson, T. Urban Microclimate: Designing the Spaces between Buildings; Earthscan: London, UK, 2011. [Google Scholar]
- Zeger, S.L.; Thomas, D.; Dominici, F.; Samet, J.M.; Schwartz, J.; Dockery, D.; Cohen, A. Exposure measurement error in time-series studies of air pollution: Concepts and consequences. Environ. Health Perspect. 2000, 108, 419–426. [Google Scholar] [CrossRef]
- Mirzaei, P.A.; Haghighat, F. Approaches to study Urban Heat Island—Abilities and limitations. Build. Environ. 2010, 45, 2192–2201. [Google Scholar] [CrossRef]
- Rosenfeld, A.; Dorman, M.; Schwartz, J.; Novack, V.; Just, A.C.; Kloog, I. Estimating daily minimum, maximum, and mean near surface air temperature using hybrid satellite models across Israel. Environ. Res. 2017, 159, 297–312. [Google Scholar] [CrossRef]
- Kloog, I.; Nordio, F.; Lepeule, J.; Padoan, A.; Lee, M.; Auffray, A.; Schwartz, J. Modelling spatio-temporally resolved air temperature across the complex geo-climate area of France using satellite-derived land surface temperature data. Int. J. Climatol. 2017, 37, 296–304. [Google Scholar] [CrossRef]
- Janatian, N.; Sadeghi, M.; Sanaeinejad, S.H.; Bakhshian, E.; Farid, A.; Hasheminia, S.M.; Ghazanfari, S. A statistical framework for estimating air temperature using MODIS land surface temperature data. Int. J. Climatol. 2017, 37, 1181–1194. [Google Scholar] [CrossRef]
- Kloog, I.; Chudnovsky, A.; Koutrakis, P.; Schwartz, J. Temporal and spatial assessments of minimum air temperature using satellite surface temperature measurements in Massachusetts, USA. Sci. Total Environ. 2012, 432, 85–92. [Google Scholar] [CrossRef] [Green Version]
- Kilibarda, M.; Hengl, T.; Heuvelink, G.B.M.; Gräler, B.; Pebesma, E.; Perčec Tadić, M.; Bajat, B. Spatio-temporal interpolation of daily temperatures for global land areas at 1 km resolution. J. Geophys. Res. Atmos. 2014, 119, 2294–2313. [Google Scholar] [CrossRef] [Green Version]
- Oyler, J.W.; Ballantyne, A.; Jencso, K.; Sweet, M.; Running, S.W. Creating a topoclimatic daily air temperature dataset for the conterminous United States using homogenized station data and remotely sensed land skin temperature. Int. J. Climatol. 2015, 35, 2258–2279. [Google Scholar] [CrossRef]
- Meyer, H.; Katurji, M.; Appelhans, T.; Müller, M.U.; Nauss, T.; Roudier, P.; Zawar-Reza, P. Mapping daily air temperature for Antarctica Based on MODIS LST. Remote Sens. 2016, 8, 732. [Google Scholar] [CrossRef] [Green Version]
- Li, L.; Zha, Y. Mapping relative humidity, average and extreme temperature in hot summer over China. Sci. Total Environ. 2018, 615, 875–881. [Google Scholar] [CrossRef]
- Hough, I.; Just, A.C.; Zhou, B.; Dorman, M.; Lepeule, J.; Kloog, I. A multi-resolution air temperature model for France from MODIS and Landsat thermal data. Environ. Res. 2020, 183, 109244. [Google Scholar] [CrossRef]
- Prigent, C.; Aires, F.; Rossow, W.B. Land surface skin temperatures from a combined analysis of microwave and infrared satellite observations for an all-weather evaluation of the differences between air and skin temperatures. J. Geophys. Res. 2003, 108, 1–14. [Google Scholar] [CrossRef]
- Prihodko, L.; Goward, S.S.N. Estimation of air temperature from remotely sensed surface observations. Remote Sens. Environ. 1997, 4257, 335–346. [Google Scholar] [CrossRef]
- Zhou, B.; Erell, E.; Hough, I.; Rosenblatt, J.; Just, A.C.; Novack, V.; Kloog, I. Estimating near-surface air temperature across Israel using a machine learning based hybrid approach. Int. J. Climatol. 2020. [Google Scholar] [CrossRef] [Green Version]
- Wood, S.N. Generalized Additive Models, 2nd ed.; Chapman and Hall/CRC: London, UK, 2017; ISBN 9781315370279. [Google Scholar]
- Hastie, T.; Tibshirani, R. Generalized Additive Models. In Wiley StatsRef: Statistics Reference Online; John Wiley & Sons, Ltd.: Chichester, UK, 2014. [Google Scholar]
- Di, Q.; Amini, H.; Shi, L.; Kloog, I.; Silvern, R.; Kelly, J.; Sabath, M.B.; Choirat, C.; Koutrakis, P.; Lyapustin, A.; et al. An ensemble-based model of PM2.5 concentration across the contiguous United States with high spatiotemporal resolution. Environ. Int. 2019, 130, 104909. [Google Scholar] [CrossRef]
- Ravindra, K.; Rattan, P.; Mor, S.; Aggarwal, A.N. Generalized additive models: Building evidence of air pollution, climate change and human health. Environ. Int. 2019, 132, 104987. [Google Scholar] [CrossRef]
- Shtein, A.; Kloog, I.; Schwartz, J.; Silibello, C.; Michelozzi, P.; Gariazzo, C.; Viegi, G.; Forastiere, F.; Karnieli, A.; Just, A.C.; et al. Estimating daily PM2.5 and PM10 over Italy using an ensemble model. Environ. Sci. Technol. 2019, 54, 120–128. [Google Scholar] [CrossRef]
- Central Bureau of Statistics Statistical Abstract of Israel 2018. Available online: http://www.cbs.gov.il/reader/?MIval=%2Fshnaton%2Fshnatone_new.htm&CYear=2018&Vol=69&CSubject=2&sa=Continue (accessed on 12 May 2019).
- Goldreich, Y. The Climate of Israel; Springer US: Boston, MA, USA, 2003; ISBN 978-1-4613-5200-6. [Google Scholar]
- Copernicus Climate Change Service (C3S) ERA5: Fifth Generation of ECMWF Atmospheric Reanalyses of the Global Climate. Copernicus Climate Change Service Climate Data Store (CDS). Available online: https://cds.climate.copernicus.eu/cdsapp#!/dataset/reanalysis-era5-single-levels?tab=overview (accessed on 20 January 2019).
- Jin, M.; Dickinson, R.E. Land surface skin temperature climatology: Benefitting from the strengths of satellite observations. Environ. Res. Lett. 2010, 5, 44004. [Google Scholar] [CrossRef] [Green Version]
- Pebesma, E. Simple Features for R: Standardized Support for Spatial Vector Data. R J. 2018, 10, 439–446. [Google Scholar] [CrossRef] [Green Version]
- Esri. ArcGIS Desktop: Release 10.6; Environmental Systems Research Institute: Redlands, CA, USA, 2018. [Google Scholar] [CrossRef] [Green Version]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining-KDD ’16, San Francisco, CA, USA, 13–17 August 2016; ACM Press: New York, NY, USA, 2016; Volume 13, pp. 785–794. [Google Scholar]
- Halevy, A.; Norvig, P.; Pereira, F. The Unreasonable Effectiveness of Data. IEEE Intell. Syst. 2009, 24, 8–12. [Google Scholar] [CrossRef]
- Bischl, B.; Lang, M.; Kotthoff, L.; Schiffner, J.; Richter, J.; Studerus, E.; Casalicchio, G.; Jones, Z.M. mlr: Machine learning in R. J. Mach. Learn. Res. 2016, 17, 5938–5942. [Google Scholar]
- Wright, M.N.; Ziegler, A. ranger: A Fast Implementation of Random Forests for High Dimensional Data in C++ and R. J. Stat. Softw. 2017, 77. [Google Scholar] [CrossRef] [Green Version]
- Chen, T.; He, T.; Benesty, M.; Khotilovich, V.; Tang, Y.; Cho, H.; Chen, K.; Mitchell, R.; Cano, I.; Zhou, T.; et al. xgboost: Extreme Gradient Boosting, R Package Version 0.90.0.2. 2019. Available online: https://cran.r-project.org/package=xgboost (accessed on 3 April 2020).
- Probst, P.; Wright, M.N.; Boulesteix, A.L. Hyperparameters and tuning strategies for random forest. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2019, 9, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Thomas, J.; Coors, S.; Bischl, B. Automatic Gradient Boosting. arXiv 2018, arXiv:1807.03873. [Google Scholar]
- Kloog, I.; Nordio, F.; Coull, B.A.; Schwartz, J. Predicting spatiotemporal mean air temperature using MODIS satellite surface temperature measurements across the Northeastern USA. Remote Sens. Environ. 2014, 150, 132–139. [Google Scholar] [CrossRef]
- Rysman, J.F.; Lemaître, Y.; Moreau, E. Spatial and temporal variability of rainfall in the Alps-Mediterranean Euroregion. J. Appl. Meteorol. Climatol. 2016, 55, 655–671. [Google Scholar] [CrossRef] [Green Version]
- Yang, S.; Smith, E.A. Convective-stratiform precipitation variability ar seasonal scale from 8 yr of TRMM observations: Implications for multiple modes of diurnal variability. J. Clim. 2008, 21, 4087–4114. [Google Scholar] [CrossRef]
- Bivand, R.S.; Pebesma, E.J.; Gómez-Rubio, V. Applied Spatial Data Analysis with R; Springer: New York, NY, USA, 2013; Volume 1, ISBN 0387781706. [Google Scholar]
- Ord, J.K.; Getis, A. Local Spatial Autocorrelation Statistics: Distributional Issues and an Application. Geogr. Anal. 1995, 27, 286–306. [Google Scholar] [CrossRef]
- Getis, A.; Ord, J.K. Local spatial statistics: An overview. In Spatial Analysis: Modeling in A GIS Environment; Longley, P., Batty, M., Eds.; John Wiley & Sons: New York, NY, USA, 1996; pp. 261–277. [Google Scholar]
- Oyler, J.W.; Dobrowski, S.Z.; Holden, Z.A.; Running, S.W. Remotely sensed land skin temperature as a spatial predictor of air temperature across the conterminous United States. J. Appl. Meteorol. Climatol. 2016, 55, 1441–1457. [Google Scholar] [CrossRef]
- Zhou, B.; Kaplan, S.; Peeters, A.; Kloog, I.; Erell, E. “Surface”, “satellite” or “simulation”: Mapping intra-urban microclimate variability in a desert city. Int. J. Climatol. 2019, 40, 3099–3117. [Google Scholar] [CrossRef] [Green Version]
- Stewart, I.D.; Oke, T.R. Local Climate Zones for Urban Temperature Studies. Bull. Am. Meteorol. Soc. 2012, 93, 1879–1900. [Google Scholar] [CrossRef]
- Meyer, H.; Reudenbach, C.; Hengl, T.; Katurji, M.; Nauss, T. Improving performance of spatio-temporal machine learning models using forward feature selection and target-oriented validation. Environ. Model. Softw. 2018, 101, 1–9. [Google Scholar] [CrossRef]
- Georgescu, M.; Moustaoui, M.; Mahalov, A.; Dudhia, J. An alternative explanation of the semiarid urban area “oasis effect”. J. Geophys. Res. Atmos. 2011, 116. [Google Scholar] [CrossRef]
- Brazel, A.; Selover, N.; Vose, R.; Heisler, G. The tale of two climates—Baltimore and Phoenix urban LTER sites. Clim. Res. 2000, 15, 123–135. [Google Scholar] [CrossRef]
- Zhou, B.; Rybski, D.; Kropp, J.P. On the statistics of urban heat island intensity. Geophys. Res. Lett. 2013, 40, 5486–5491. [Google Scholar] [CrossRef]
- Zakšek, K.; Oštir, K. Downscaling land surface temperature for urban heat island diurnal cycle analysis. Remote Sens. Environ. 2012, 117, 114–124. [Google Scholar] [CrossRef]



















© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, B.; Erell, E.; Hough, I.; Shtein, A.; Just, A.C.; Novack, V.; Rosenblatt, J.; Kloog, I. Estimation of Hourly near Surface Air Temperature Across Israel Using an Ensemble Model. Remote Sens. 2020, 12, 1741. https://doi.org/10.3390/rs12111741
Zhou B, Erell E, Hough I, Shtein A, Just AC, Novack V, Rosenblatt J, Kloog I. Estimation of Hourly near Surface Air Temperature Across Israel Using an Ensemble Model. Remote Sensing. 2020; 12(11):1741. https://doi.org/10.3390/rs12111741
Chicago/Turabian StyleZhou, Bin, Evyatar Erell, Ian Hough, Alexandra Shtein, Allan C. Just, Victor Novack, Jonathan Rosenblatt, and Itai Kloog. 2020. "Estimation of Hourly near Surface Air Temperature Across Israel Using an Ensemble Model" Remote Sensing 12, no. 11: 1741. https://doi.org/10.3390/rs12111741
APA StyleZhou, B., Erell, E., Hough, I., Shtein, A., Just, A. C., Novack, V., Rosenblatt, J., & Kloog, I. (2020). Estimation of Hourly near Surface Air Temperature Across Israel Using an Ensemble Model. Remote Sensing, 12(11), 1741. https://doi.org/10.3390/rs12111741