Secchi Disk Depth Estimation from China’s New Generation of GF-5 Hyperspectral Observations Using a Semi-Analytical Scheme
Abstract
:1. Introduction
2. Study Areas and Datasets
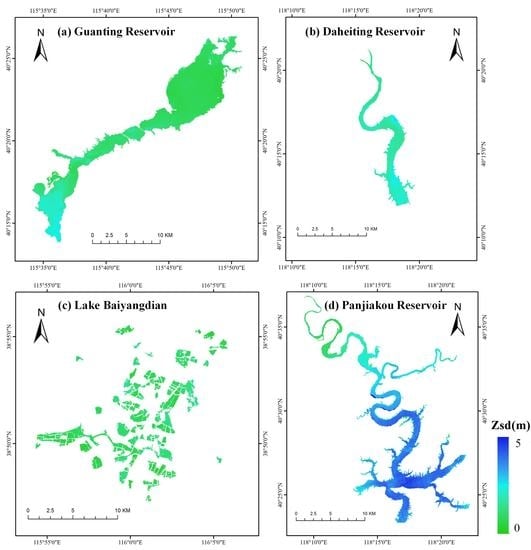
2.1. Study Areas and In Situ Measurements
2.2. Satellite Data Acquisition and Preprocessing
3. Secchi Disk Depth Estimation Method
3.1. IOPs Estimation Using the QAA Method
3.2. Retrieval Using IOPs
3.3. Estimation Based on and
3.4. Accuracy Assessment Method
4. Results
4.1. Estimation from In Situ Measurements
4.2. Estimation Scheme for AHSI Imagery
- (1)
- Samples collected within 3 h and before/after 1 day both yielded with high accuracies on the AHSI images, which is likely owing to the stable weather conditions (i.e., no strong wind or rainfall) during the image acquisition and in situ measurement.
- (2)
- The from the samples collected within 3 h is higher than that the other group, indicating that the image-retrieved has better consistency with the in situ measured on the same day.
- (3)
- Samples collected before/after 1 day have smaller MAE and MRE than those collected on the same day. This is because highly turbid sampling sites (i.e., < 0.7 m) included in the latter have worse predictions, leading to greater MAE and MRE in this group of samples.
5. Discussion
5.1. AHSI Atmospheric Correction Performance Evaluation
5.2. Estimation Methods Evaluation
- (1)
- -based SAM evaluationBased on the in situ acquired AHSI , yielded good predictions only for values higher than 3.0 m due to its limitations in turbid water. In addition, the semi-analytical method with was evaluated as being capable of retrieving the for an oligo- to mesotrophic inland reservoir [37], but acquired an average relative error of 75.05%.
- (2)
- -based SAM evaluationwas developed with limited samples collected from Lake Taihu, with sensitivity to water contents and optical properties as mentioned in Reference [31]. Specifically, the range of Lake Taihu is 0–0.9 m, which is distinct from the water clarity range of our study regions. This is likely the reason for poor performance in terms of the retrieval in our study regions.
- (3)
- -based SAM evaluationThe estimated values based on the using image and AHSI in situ have similar MAEs and MREs. In other words, the image with is generally consistent with the AHSI in-situ generated results when using the -based semi-analytical method, despite an approximated for the image that is generally higher than the in situ measured reflectance due to insufficient atmospheric correction. Since and are mainly affected by the shape and magnitude of the , respectively [38], retrieved from the image is consistent with the in situ-derived values. In addition, affects and to a more extent than does , and therefore, the image-retrieved values are comparable to the in situ-derived results. However, the estimation accuracies were different at various ranges between the image and in situ derived . For the clarity range of 1–3 m, the estimated image has poorer accuracies (MRE of 29.1%) than the in situ determined (MRE of 18.2%). In contrast, the image-generated was better than that of the in situ values for <1 m and >3 m clarity conditions.
- (4)
- -based SAM evaluationFor the -based method, the image , however, acquired distinct results compared with those estimated from the AHSI band-equivalent in situ . Unlike the AHSI in situ that generated desirable predictions using the , the values calculated from the image have significantly poorer accuracies. Specifically, the MRE is 47.4% for a of less than 1 m, while the MRE increases to 60.9 and 75.6% for values ranging from 1–3 m and >3 m, respectively. Moreover, the absolute error also increases from 0.42 to 1.24 m. Such large errors are unacceptable when estimating the water clarity in ranges from 0.3 to 4.5 m. Figure 6 shows that image is higher than in situ but with similar spectral shapes. However, the ratio of image and in-situ at 708 nm is greater than that at 555 nm, since is much lower in the 708 nm band. Therefore, the use of 708 nm in algorithm leads to an overestimation of and , which finally results in an underestimation for on AHSI images.
5.3. Validation Limitations
5.4. GF-5 Applicability to Retrieval
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Le, C.; Zha, Y.; Li, Y.; Sun, D.; Lu, H.; Yin, B. Eutrophication of lake waters in China: Cost, causes, and control. Environ. Manag. 2010, 45, 662–668. [Google Scholar] [CrossRef] [PubMed]
- Zhang, K.; Shi, H.; Peng, J.; Wang, Y.; Xiong, X.; Wu, C.; Lam, P.K. Microplastic pollution in China’s inland water systems: A review of findings, methods, characteristics, effects, and management. Sci. Total Environ. 2018, 630, 1641–1653. [Google Scholar] [CrossRef] [PubMed]
- Behmel, S.; Damour, M.; Ludwig, R.; Rodriguez, M.J. Water quality monitoring strategies—A review and future perspectives. Sci. Total Environ. 2016, 571, 1312–1329. [Google Scholar] [CrossRef] [PubMed]
- Becker, R.H.; Sayers, M.; Dehm, D.; Shuchman, R.; Quintero, K.; Bosse, K.; Sawtell, R. Unmanned aerial system based spectroradiometer for monitoring harmful algal blooms: A new paradigm in water quality monitoring. J. Great Lakes Res. 2019, 45, 444–453. [Google Scholar] [CrossRef]
- Shi, K.; Zhang, Y.; Zhu, G.; Qin, B.; Pan, D. Deteriorating water clarity in shallow waters: Evidence from long term MODIS and in-situ observations. Int. J. Appl. Earth Obs. Geoinf. 2018, 68, 287–297. [Google Scholar] [CrossRef]
- Holmes, R.W. The Secchi disk in turbid coastal waters 1. Limnol. Oceanogr. 1970, 15, 688–694. [Google Scholar] [CrossRef]
- Boyce, D.G.; Lewis, M.; Worm, B. Integrating global chlorophyll data from 1890 to 2010. Limnol. Oceanogr. Methods 2012, 10, 840–852. [Google Scholar] [CrossRef]
- Swift, T.J.; Perez-Losada, J.; Schladow, S.G.; Reuter, J.E.; Jassby, A.D.; Goldman, C.R. Water clarity modeling in lake Tahoe: Linking suspended matter characteristics to Secchi depth. Aquat. Sci. 2006, 68, 1–15. [Google Scholar] [CrossRef]
- Doron, M.; Babin, M.; Hembise, O.; Mangin, A.; Garnesson, P. Ocean transparency from space: Validation of algorithms estimating Secchi depth using MERIS, MODIS and SeaWiFS data. Remote Sens. Environ. 2011, 115, 2986–3001. [Google Scholar] [CrossRef]
- Alikas, K.; Kratzer, S. Improved retrieval of Secchi depth for optically-complex waters using remote sensing data. Ecol. Indic. 2017, 77, 218–227. [Google Scholar] [CrossRef]
- Olmanson, L.G.; Bauer, M.E.; Brezonik, P.L. A 20-year Landsat water clarity census of Minnesota’s 10,000 lakes. Remote Sens. Environ. 2008, 112, 4086–4097. [Google Scholar] [CrossRef]
- McCullough, I.M.; Loftin, C.S.; Sader, S.A. Combining lake and watershed characteristics with Landsat TM data for remote estimation of regional lake clarity. Remote Sens. Environ. 2012, 123, 109–115. [Google Scholar] [CrossRef]
- Mancino, G.; Nolè, A.; Urbano, V.; Amato, M.; Ferrara, A. Assessing water quality by remote sensing in small lakes: The case study of Monticchio lakes in southern Italy. iFor.-Biogeosci. For. 2009, 2, 154. [Google Scholar] [CrossRef] [Green Version]
- Thiemann, S.; Kaufmann, H. Lake water quality monitoring using hyperspectral airborne data—A semiempirical multisensor and multitemporal approach for the Mecklenburg Lake District, Germany. Remote Sens. Environ. 2002, 81, 228–237. [Google Scholar] [CrossRef]
- Binding, C.E.; Greenberg, T.A.; Watson, S.B.; Rastin, S.; Gould, J. Long term water clarity changes in north America’s Great Lakes from multi-sensor satellite observations. Limnol. Oceanogr. 2015, 60, 1976–1995. [Google Scholar] [CrossRef]
- Lee, Z.; Shang, S.; Hu, C.; Du, K.; Weidemann, A.; Hou, W.; Lin, J.; Lin, G. Secchi disk depth: A new theory and mechanistic model for underwater visibility. Remote Sens. Environ. 2015, 169, 139–149. [Google Scholar] [CrossRef] [Green Version]
- Lee, Z.; Carder, K.L.; Arnone, R.A. Deriving inherent optical properties from water color: A multiband quasi-analytical algorithm for optically deep waters. Appl. Opt. 2002, 41, 5755–5772. [Google Scholar] [CrossRef]
- Shang, S.; Lee, Z.; Shi, L.; Lin, G.; Wei, G.; Li, X. Changes in water clarity of the Bohai Sea: Observations from MODIS. Remote Sens. Environ. 2016, 186, 22–31. [Google Scholar] [CrossRef] [Green Version]
- Feng, L.; Hou, X.; Zheng, Y. Monitoring and understanding the water transparency changes of fifty large lakes on the Yangtze Plain based on long-term MODIS observations. Remote Sens. Environ. 2019, 221, 675–686. [Google Scholar] [CrossRef]
- Liu, Y.N.; Sun, D.X.; Hu, X.N.; Ye, X.; Li, Y.D.; Liu, S.F.; Cao, K.Q.; Chai, M.Y.; Zhou, W.Y.N.; Zhang, L.; et al. The Advanced Hyperspectral Imager: Aboard China’s Gaofen-5 satellite. IEEE Geosci. Remote Sens. Mag. 2019, 7, 23–32. [Google Scholar] [CrossRef]
- Liu, Y.N.; Sun, D.X.; Cao, K.Q.; Liu, S.F.; Chai, M.Y.; Liang, J.; Yuan, J. Evaluation of GF-5 AHSI on-orbit instrument radiometric performance. J. Remote Sens. 2020, 24, 352–359. (In Chinese) [Google Scholar]
- Tang, J.W.; Tian, G.L.; Wang, X.Y.; Wang, X.M.; Song, Q.J. The methods of water spectra measurement and analysis I: Above-water method. J. Remote Sens. 2004, 8, 37–44. [Google Scholar]
- Mueller, J.L.; Morel, A.; Frouin, R.; Davis, C.; Arnone, R.; Carder, K.; Lee, Z.P.; Steward, R.G.; Hooker, S.; Mobley, C.D.; et al. Ocean Optics Protocols for Satellite Ocean Color Sensor Validation, Revision 4. Volume III: Radiometric Measurements and Data Analysis Protocols; Goddard Space Flight Space Center: Greenbelt, MD, USA, 2003. [Google Scholar]
- Ruddick, K.G.; Voss, K.; Banks, A.C.; Boss, E.; Castagna, A.; Frouin, R.; Hieronymi, M.; Jamet, C.; Johnson, B.C.; Kuusk, J.; et al. A review of protocols for fiducial reference measurements of downwelling irradiance for the validation of satellite remote sensing data over water. Remote Sens. 2019, 11, 1742. [Google Scholar] [CrossRef] [Green Version]
- Mobley, C.D. Estimation of the remote-sensing reflectance from above-surface measurements. Appl. Opt. 1999, 38, 7442–7455. [Google Scholar] [CrossRef]
- Lee, Z.; Ahn, Y.H.; Mobley, C.; Arnone, R. Removal of surface-reflected light for the measurement of remote-sensing reflectance from an above-surface platform. Opt. Express 2010, 18, 26313–26324. [Google Scholar] [CrossRef]
- Zhang, X.; He, S.; Shabani, A.; Zhai, P.W.; Du, K. Spectral sea surface reflectance of skylight. Opt. Express 2017, 25, A1–A13. [Google Scholar] [CrossRef]
- Kaufman, Y.J.; Wald, A.E.; Remer, L.A.; Gao, B.C.; Li, R.R.; Flynn, L. The MODIS 2.1-μm channel-correlation with visible reflectance for use in remote sensing of aerosol. IEEE Trans. Geosci. Remote Sens. 1997, 35, 1286–1298. [Google Scholar] [CrossRef]
- Zhang, F.; Li, J.; Zhang, B.; Shen, Q.; Ye, H.; Wang, S.; Lu, Z. A simple automated dynamic threshold extraction method for the classification of large water bodies from Landsat-8 OLI water index images. Int. J. Remote Sens. 2018, 39, 3429–3451. [Google Scholar] [CrossRef]
- Lee, Z.; Shang, S.; Qi, L.; Yan, J.; Lin, G. A semi-analytical scheme to estimate Secchi-disk depth from Landsat-8 measurements. Remote Sens. Environ. 2016, 177, 101–106. [Google Scholar] [CrossRef]
- Le, C.F.; Li, Y.M.; Zha, Y.; Sun, D.; Yin, B. Validation of a quasi-analytical algorithm for highly turbid eutrophic water of Meiliang Bay in Taihu Lake, China. IEEE Trans. Geosci. Remote Sens. 2009, 47, 2492–2500. [Google Scholar]
- Mishra, S.; Mishra, D.R.; Lee, Z. Bio-optical inversion in highly turbid and cyanobacteria-dominated waters. IEEE Trans. Geosci. Remote Sens. 2013, 52, 375–388. [Google Scholar] [CrossRef]
- Yang, W.; Matsushita, B.; Chen, J.; Yoshimura, K.; Fukushima, T. Retrieval of inherent optical properties for turbid inland waters from remote-sensing reflectance. IEEE Trans. Geosci. Remote Sens. 2012, 51, 3761–3773. [Google Scholar] [CrossRef]
- Lee, Z.; Lubac, B.; Werdell, J.; Arnone, R. An Update of the Quasi-Analytical Algorithm (QAA_v5). International Ocean Color Group Software Report. 2009, pp. 1–9. Available online: http://www.ioccg.org/groups/Software_OCA/QAA_v5.pdf (accessed on 1 January 2020).
- Lee, Z.; Hu, C.; Shang, S.; Du, K.; Lewis, M.; Arnone, R.; Brewin, R. Penetration of uv-visible solar radiation in the global oceans: Insights from ocean color remote sensing. J. Geophys. Res. Ocean. 2013, 118, 4241–4255. [Google Scholar] [CrossRef] [Green Version]
- Preisendorfer, R.W. Secchi disk science: Visual optics of natural waters 1. Limnol. Oceanogr. 1986, 31, 909–926. [Google Scholar] [CrossRef] [Green Version]
- Rodrigues, T.; Alcântara, E.; Watanabe, F.; Imai, N. Retrieval of Secchi disk depth from a reservoir using a semi-analytical scheme. Remote Sens. Environ. 2017, 198, 213–228. [Google Scholar] [CrossRef] [Green Version]
- Shang, S.; Lee, Z.; Lin, G.; Hu, C.; Shi, L.; Zhang, Y.; Li, X.; Wu, J.; Yan, J. Sensing an intense phytoplankton bloom in the western Taiwan Strait from radiometric measurements on a UAV. Remote Sens. Environ. 2017, 198, 85–94. [Google Scholar] [CrossRef]
- Rodrigues, T.; Alcântara, E.; Mishra, D.R.; Watanabe, F.; Bernardo, N.; Rotta, L.; Imai, N.; Astuti, I. Performance of existing QAAs in Secchi disk depth retrieval in phytoplankton and dissolved organic matter dominated inland waters. J. Appl. Remote Sens. 2018, 12, 036017. [Google Scholar] [CrossRef]
- Luis, K.M.; Rheuban, J.E.; Kavanaugh, M.T.; Glover, D.M.; Wei, J.; Lee, Z.; Doney, S.C. Capturing coastal water clarity variability with Landsat 8. Mar. Pollut. Bull. 2019, 145, 96–104. [Google Scholar] [CrossRef]






| No. | Study Region | Longitude | Latitude | In Situ Data | N | (m) | ||
|---|---|---|---|---|---|---|---|---|
| Acquisition Date | Mean | Min | Max | |||||
| 1 | Guanting Reservoir | 115.73 E | 40.35 N | 5/22/2019 | 18 | 1.16 | 0.30 | 2.15 |
| 2 | Lake Baiyangdian | 116.01 E | 38.82 N | 5/21/2019 | 16 | 1.13 | 0.70 | 1.60 |
| 5/22/2019 | 13 | 1.13 | 0.55 | 1.70 | ||||
| 3 | Panjiakou Reservoir | 118.29 E | 40.43 N | 9/24/2019 | 25 | 3.41 | 1.20 | 4.50 |
| 4 | Daheiting Reservoir | 118.31 E | 40.28 N | 9/25/2019 | 12 | 1.38 | 0.85 | 2.10 |
| Step | Property | |||
|---|---|---|---|---|
| 0 | same as | same as | ||
| 1 | same as | same as | ||
| 2 | ||||
| 3 | same as | |||
| 4 | same as | |||
| 5 | same as | same as | ||
| 6 | same as | same as |
| Range (m) | N | |||||
|---|---|---|---|---|---|---|
| MAE (m) | 0.3–1.0 | 23 | 0.34 | 0.49 | 0.13 | 0.18 |
| 1.0–3.0 | 43 | 0.25 | 0.44 | 0.46 | 0.21 | |
| >3.0 | 18 | 0.57 | 0.56 | 1.96 | 1.26 | |
| 0.3–4.5 | 84 | 0.35 | 0.48 | 0.69 | 0.42 | |
| MRE | 0.3–1.0 | 23 | 48.4% | 72.1% | 15.5% | 22.8% |
| 1.0–3.0 | 43 | 18.2% | 28.7% | 28.7% | 12.8% | |
| >3.0 | 18 | 14.7% | 14.2% | 50.3% | 32.3% | |
| 0.3–4.5 | 84 | 25.7% | 37.5% | 29.7% | 19.7% |
| Range (m) | N | MAE (m) | MRE | ||
|---|---|---|---|---|---|
| 0.3–1.0 | 23 | 0.22 | 0.39 | 33.1% | 47.4% |
| 1.0–3.0 | 43 | 0.46 | 0.98 | 29.1% | 60.9% |
| >3.0 | 18 | 0.24 | 2.94 | 6.3% | 75.6% |
| Total | 84 | 0.35 | 1.24 | 25.3% | 60.4% |
| Time Difference between | Range (m) | N | MAE (m) | MRE | |
|---|---|---|---|---|---|
| In Situ Data and AHSI Image | |||||
| Within 3 h | 0.3–4.5 | 56 | 0.38 | 26.1% | 0.871 |
| Before/after 1 day | 0.7–2.1 | 28 | 0.28 | 23.7% | 0.502 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Xiao, C.; Li, J.; Zhang, F.; Wang, S. Secchi Disk Depth Estimation from China’s New Generation of GF-5 Hyperspectral Observations Using a Semi-Analytical Scheme. Remote Sens. 2020, 12, 1849. https://doi.org/10.3390/rs12111849
Liu Y, Xiao C, Li J, Zhang F, Wang S. Secchi Disk Depth Estimation from China’s New Generation of GF-5 Hyperspectral Observations Using a Semi-Analytical Scheme. Remote Sensing. 2020; 12(11):1849. https://doi.org/10.3390/rs12111849
Chicago/Turabian StyleLiu, Yao, Chenchao Xiao, Junsheng Li, Fangfang Zhang, and Shenglei Wang. 2020. "Secchi Disk Depth Estimation from China’s New Generation of GF-5 Hyperspectral Observations Using a Semi-Analytical Scheme" Remote Sensing 12, no. 11: 1849. https://doi.org/10.3390/rs12111849
APA StyleLiu, Y., Xiao, C., Li, J., Zhang, F., & Wang, S. (2020). Secchi Disk Depth Estimation from China’s New Generation of GF-5 Hyperspectral Observations Using a Semi-Analytical Scheme. Remote Sensing, 12(11), 1849. https://doi.org/10.3390/rs12111849