Gudalur Spectral Target Detection (GST-D): A New Benchmark Dataset and Engineered Material Target Detection in Multi-Platform Remote Sensing Data
Abstract
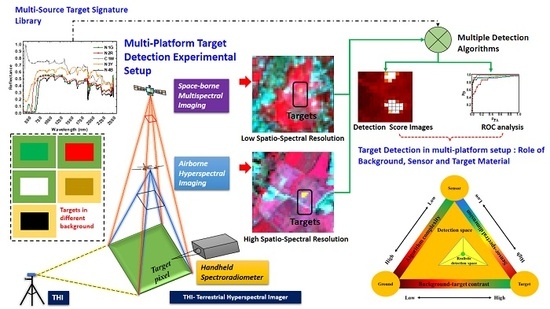
:1. Introduction
2. Materials and Methods
2.1. Experimental Design
2.2. Data Pre-Processing
2.2.1. Reference Spectral Data Sources and Pre-Processing
2.2.2. Pre-Processing of Airborne and Spaceborne Imagery
2.3. Experimental Implementation of Target Detection
Target Detection Algorithms
2.4. Quantitative Description of Target Detection Algorithms
2.5. Validation, and Quantitative Spectral Analysis
3. Results
3.1. In-Situ Measurements as Reference Target Spectra
3.1.1. Target Detection in Airborne Hyperspectral Imagery
3.1.2. Target Detection in Spaceborne Remote Sensing Imagery
3.2. Ground-Based Hyperspectral Imagery (THI) as Reference Target Spectra
3.2.1. Target Detection in Airborne Hyperspectral Imagery
3.2.2. Target Detection in Spaceborne Remote Sensing Imagery
3.3. Target Reference Spectra from the Airborne Hyperspectral Imagery
3.3.1. Target Detection in Airborne Hyperspectral Imagery
3.3.2. Target Detection in Spaceborne Multispectral Imagery
3.4. Target Reference Spectra from the Spaceborne Multispectral Imagery
3.5. Quantitative Spectral Similarity Analysis
4. Discussion
4.1. Spectral Conformity of the Reference Target Spectra from the Ground to Spaceborne Platform
4.2. Target–Background Interaction—Role of Context
4.3. Detection Algorithms and Their Functional Categorization
4.4. Key Elements of Influence in Target Detection
4.5. Experimental Dataset
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Baldridge, A.M.; Hook, S.J.; Grove, C.I.; Rivera, G. The ASTER spectral library version 2.0. Remote Sens. Environ. 2009, 113, 711–715. [Google Scholar] [CrossRef]
- Kokaly, R.F.; Clark, R.N.; Swayze, G.A.; Livo, K.E.; Hoefen, T.M.; Pearson, N.C.; Wise, R.A.; Benzel, W.M.; Lowers, H.A.; Driscoll, R.L.; et al. USGS Spectral Library Version 7. Geol. Surv. Data Ser. 2017. [Google Scholar] [CrossRef]
- Meerdink, S.K.; Hook, S.J.; Roberts, D.A.; Abbott, E.A. The ECOSTRESS spectral library version 1.0. Remote Sens. Environ. 2019, 230, 111196. [Google Scholar] [CrossRef]
- Cohen, Y.; August, Y.; Blumberg, D.G.; Rotman, S.R. Evaluating subpixel target detection algorithms in hyperspectral imagery. J. Electr. Comput. Eng. 2012. [Google Scholar] [CrossRef]
- Archer, C.; Morgenstern, J.; Musallam, R.N. Improved target recognition with live atmospheric correction. In Algorithms and Technologies for Multispectral, Hyperspectral, and Ultraspectral ImageryXIX; International Society for Optics and Photonics: Baltimore, MD, USA, 18 May 2013; Volume 8743, p. 87430. [Google Scholar]
- Yadav, D.; Arora, M.K.; Tiwari, K.C.; Ghosh, J.K. Parameters affecting target detection in VNIR and SWIR range. Egypt. J. Remote Sens. Space Sci. 2018, 21, 325–333. [Google Scholar] [CrossRef]
- Cheng, G.; Han, J. A survey on object detection in optical remote sensing images. ISPRS J. Photogramm. Remote Sens. 2016, 117, 11–28. [Google Scholar] [CrossRef] [Green Version]
- Kanjir, U.; Greidanus, H.; Oštir, K. Vessel detection and classification from spaceborne optical images: A literature survey. Remote Sens. Environ. 2018, 207, 1–26. [Google Scholar] [CrossRef] [PubMed]
- Briottet, X.; Boucher, Y.; Dimmeler, A.; Malaplate, A.; Cini, A.; Diani, M.; Bekman, H.H.P.T.; Schwering, P.; Skauli, T.; Kasen, I.; et al. Military applications of hyperspectral imagery. In Targets and Backgrounds XII: Characterization and Representation; International Society for Optics and Photonics: Orlando (Kissimmee), FL, USA, 4 May 2006; Volume 6239, p. 62390. [Google Scholar]
- Yuen, P.W.; Richardson, M. An introduction to hyperspectral imaging and its application for security, surveillance and target acquisition. Imaging Sci. J. 2010, 58, 241–253. [Google Scholar] [CrossRef]
- Molan, Y.E.; Refahi, D.; Tarashti, A.H. Mineral mapping in the Maherabad area, eastern Iran, using the HyMap remote sensing data. Int. J. Appl. Earth Obs. Geoinf. 2014, 27, 117–127. [Google Scholar] [CrossRef]
- Hou, Y.; Zhang, Y.; Yao, L.; Liu, X.; Wang, F. Mineral target detection based on MSCPE_BSE in hyperspectral image. In Proceedings of the 2016 IEEE InternationalGeoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 1614–1617. [Google Scholar]
- Dos Reis Salles, R.; Souza Filho, C.R.; Cudahy, T.; Vicente, L.E.; Monteiro, L.V.S. Hyperspectral remote sensing applied to uranium exploration: A case study at the Mary Kathleen metamorphic-hydrothermal U-REE deposit, NW, Queensland, Australia. J. Geochem. Explor. 2017, 179, 36–50. [Google Scholar] [CrossRef]
- Snyder, D.; Kerekes, J.; Fairweather, I.; Crabtree, R.; Shive, J.; Hager, S. Development of a web-based application to evaluate target finding algorithms. In Proceedings of the IGARSS 2008-IEEE International Geoscience and Remote Sensing Symposium, Boston, MA, USA, 7–11 July 2008; Volume 2, p. 915. [Google Scholar]
- Manolakis, D.; Marden, D.; Shaw, G.A. Hyperspectral image processing for automatic target detection applications. Linc. Lab. J. 2003, 14, 79–116. [Google Scholar]
- Acito, N.; Matteoli, S.; Rossi, A.; Diani, M.; Corsini, G. Hyperspectral airborne “Viareggio 2013 Trial” data collection for detection algorithm assessment. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 2365–2376. [Google Scholar] [CrossRef]
- Hamlin, L.; Green, R.O.; Mouroulis, P.; Eastwood, M.; Wilson, D.; Dudik, M.; Paine, C. Imaging spectrometer science measurements for terrestrial ecology. In Proceedings of the AVIRIS and New Developments. 2011 Aerospace Conference, Big Sky, MT, USA, 5–12 March 2011; pp. 1–7. [Google Scholar]
- Bhattacharya, B.K.; Green, R.O.; Rao, S.; Saxena, M.; Sharma, S.; Kumar, K.A.; Srinivasulu, P.; Sharma, S.; Dhar, D.; Bandyopadhyay, S.; et al. An overview of AVIRIS-NG airborne hyperspectral science campaign over India. Curr. Sci. 2019, 116, 1082–1088. [Google Scholar] [CrossRef]
- SVC-Field-Spectroscopy-Guide-Rev-1-2019-10-22.pdf. Available online: https://www.spectravista.com/wp-content/uploads/2019/12/SVC-Field-Spectroscopy-Guide-Rev-1-2019-10-22.pdf (accessed on 19 June 2020).
- Adler-Golden, S.; Berk, A.; Bernstein, L.S.; Richtsmeier, S.; Acharya, P.K.; Matthew, M.W.; Anderson, G.P.; Allred, C.L.; Jeong, L.S.; Chetwynd, J.H. FLAASH, a MODTRAN4 atmospheric correction package for hyperspectral data retrievals and simulations. In Summaries of the Seventh JPL Airborne Earth Science Workshop; Jet Propulsion Laboratory, California Institute of Technology: Pasadena, CA, USA, 16 January 1998; Volume 1, pp. 9–14. [Google Scholar]
- Gruninger, J.H.; Ratkowski, A.J.; Hoke, M.L. The Sequential Maximum Angle Convex Cone (SMACC) Endmember Model. In Algorithms and Technologies for Multispectral, Hyperspectral, and Ultraspectral ImageryX; International Society for Optics and Photonics: Orlando, FL, USA, 12 August 2004; Volume 5425. [Google Scholar]
- Manolakis, D.G.; Lockwood, R.B.; Cooley, T.W. Hyperspectral Imaging Remote Sensing: Physics, Sensors, and Algorithms; Cambridge University Press: Cambridge, UK, 2016. [Google Scholar]
- Kay, S.M. Fundamentals of Statistical Signal Processing: Detection Theory; Prentice Hall PTR: Upper Saddle River, NJ, USA, 1993; Volume II. [Google Scholar]
- Kruse, F.A.; Lefkoff, A.B.; Boardman, J.W.; Heidebrecht, K.B.; Shapiro, A.T.; Barloon, P.J.; Goetz, A.F.H. The spectral image processing system (SIPS)—Interactive visualization and analysis of imaging spectrometer data. Remote Sens. Environ. 1993, 44, 145–163. [Google Scholar] [CrossRef]
- Manolakis, D. Detection algorithms for hyperspectral imaging applications: A signal processing perspective. In Proceedings of the 2003 IEEE Workshop onAdvances in Techniques for Analysis of Remotely Sensed Data, Greenbelt, MD, USA, 27–28 October 2003; pp. 378–384. [Google Scholar]
- Chang, C.I. Hyperspectral Imaging: Techniques for Spectral Detection and Classification; Springer Science & Business Media: New York, NY, USA, 2003; Volume 1. [Google Scholar]
- Scharf, L.L.; McWhorter, L.T. Adaptive matched subspace detectors and adaptive coherence estimators. In Proceedings of the Conference Record of the Thirtieth Asilomar IEEE Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 3–6 November 1996; pp. 1114–1117. [Google Scholar]
- Harsanyi, J.C.; Chang, C.I. Hyperspectral image classification and dimensionality reduction: An orthogonal subspace projection approach. IEEE Trans. Geosci. Remote Sens. 1994, 32, 779–785. [Google Scholar] [CrossRef] [Green Version]
- Ren, H.; Chang, C.I. Target-constrained interference-minimized approach to subpixel target detection for hyperspectral images. Opt. Eng. 2000, 39, 3138–3146. [Google Scholar] [CrossRef]
- Fawcett, T. An introduction to ROC analysis. Pattern Recognit. Lett. 2006, 27, 861–874. [Google Scholar] [CrossRef]
- Krawczyk, B. Learning from imbalanced data: Open challenges and future directions. Prog. Artif. Intell. 2016, 5, 221–232. [Google Scholar] [CrossRef] [Green Version]
- Chang, C.I. An information-theoretic approach to spectral variability, similarity, and discrimination for hyperspectral image analysis. IEEE Trans. Inf. Theory 2000, 46, 1927–1932. [Google Scholar] [CrossRef] [Green Version]
- Robila, S.A.; Gershman, A. Spectral matching accuracy in processing hyperspectral data. In Proceedings of the IEEE International Symposium on Signals, Circuits and Systems (ISSCS 2005), Iasi, Romania, 14–15 July 2005; Volume 1, pp. 163–166. [Google Scholar]
- Van der Meer, F. The effectiveness of spectral similarity measures for the analysis of hyperspectral imagery. Int. J. Appl. Earth Obs. Geoinf. 2006, 8, 3–17. [Google Scholar] [CrossRef]
- Goodenough, A.A.; Brown, S.D. DIRSIG 5: Core design and implementation. In Algorithms and Technologies for Multispectral, Hyperspectral, and Ultraspectral ImageryXVIII; International Society for Optics and Photonics: Baltimore, MD, USA, 2012; Volume 8390, p. 83900. [Google Scholar]
- Wang, Z.; Xue, J.-H. The matched subspace detector with interaction effects. Pattern Recognit. 2017, 68, 24–37. [Google Scholar] [CrossRef]
- Matteoli, S.; Diani, M.; Theiler, J. An overview of background modeling for detection of targets and anomalies in hyperspectral remotely sensed imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2317–2336. [Google Scholar] [CrossRef]






















| Target Material | Target Name |
|---|---|
| Green nylon sheet | N1G |
| Red nylon sheet | N2R |
| White cotton sheet | C1W |
| Yellow nylon sheet | N3Y |
| Black nylon sheet | N4B |
| In-Situ Reference Spectra vs. Airborne Image Spectra | In-Situ Reference Spectra vs. Satellite Imagery Spectra | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Metric | N1G | N2R | C1W | N3Y | N4B | N1G | N2R | C1W | N3Y | N4B |
| SA | 7.623 | 10.386 | 12.273 | 8.503 | 11.617 | 8.338 | 14.111 | 15.246 | 8.008 | 19.219 |
| SID | 0.031 | 0.050 | 0.050 | 0.028 | 0.105 | 0.045 | 0.126 | 0.074 | 0.019 | 0.306 |
| SGA | 0.650 | 0.839 | 0.523 | 0.678 | 0.744 | 0.688 | 1.040 | 0.904 | 0.667 | 0.887 |
| THI Reference Spectra vs. Airborne Image Spectra | THI Reference Spectra vs. Satellite Imagery Spectra | |||||||
|---|---|---|---|---|---|---|---|---|
| Metric | N1G | N2R | N3Y | N4B | N1G | N2R | N3Y | N4B |
| SA | 15.444 | 15.762 | 20.916 | 14.268 | 13.459 | 18.181 | 16.290 | |
| SID | 0.143 | 0.101 | 0.179 | 0.172 | 0.087 | 0.136 | 0.134 | 0.176 |
| SGA | 0.775 | 0.821 | 0.943 | 0.754 | 0.898 | 1.282 | 0.288 | 0.836 |
| Airborne Reference Spectra vs. Satellite Imagery Spectra | |||||
|---|---|---|---|---|---|
| Metric | N1G | N2R | C1W | N3Y | N4B |
| SA | 4.169 | 4.431 | 13.008 | 1.406 | 6.045 |
| SID | 0.011 | 0.016 | 0.073 | 0.001 | 0.018 |
| SGA | 0.336 | 0.391 | 0.378 | 0.096 | 0.309 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jha, S.S.; Nidamanuri, R.R. Gudalur Spectral Target Detection (GST-D): A New Benchmark Dataset and Engineered Material Target Detection in Multi-Platform Remote Sensing Data. Remote Sens. 2020, 12, 2145. https://doi.org/10.3390/rs12132145
Jha SS, Nidamanuri RR. Gudalur Spectral Target Detection (GST-D): A New Benchmark Dataset and Engineered Material Target Detection in Multi-Platform Remote Sensing Data. Remote Sensing. 2020; 12(13):2145. https://doi.org/10.3390/rs12132145
Chicago/Turabian StyleJha, Sudhanshu Shekhar, and Rama Rao Nidamanuri. 2020. "Gudalur Spectral Target Detection (GST-D): A New Benchmark Dataset and Engineered Material Target Detection in Multi-Platform Remote Sensing Data" Remote Sensing 12, no. 13: 2145. https://doi.org/10.3390/rs12132145
APA StyleJha, S. S., & Nidamanuri, R. R. (2020). Gudalur Spectral Target Detection (GST-D): A New Benchmark Dataset and Engineered Material Target Detection in Multi-Platform Remote Sensing Data. Remote Sensing, 12(13), 2145. https://doi.org/10.3390/rs12132145