Evaluation of Inter-System Bias between BDS-2 and BDS-3 Satellites and Its Impact on Precise Point Positioning
Abstract
:1. Introduction
2. Methods
3. BDS-3 Precise Products Description
4. The Analysis of ISB Between BDS-2 and BDS-3
4.1. Processing Strategy for ISB
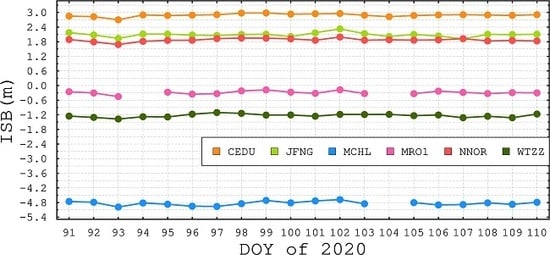
4.2. The Consistency of BDS-2 and BDS-3 Code Hardware Delays
5. The Impact of ISB on BDS PPP
5.1. Data Description and Processing Strategy
5.2. Results and Analysis
6. Discussion
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Yang, Y.; Gao, W.; Guo, S.; Mao, Y. Introduction to BeiDou-3 navigation satellite system. Navigation 2019, 66, 7–18. [Google Scholar] [CrossRef] [Green Version]
- Wang, M.; Wang, J.; Dong, D.; Meng, L.; Chen, J.; Wang, A.; Cui, H. Performance of BDS-3: Satellite visibility and dilution of precision. GPS Solut. 2019, 23, 56. [Google Scholar] [CrossRef]
- Cao, C.; Jing, G.; Luo, M. COMPASS Satellite Navigation System Development. In Proceedings of the PNT challenges and opportunities symposium, Stanford, CA, USA, 5–6 November 2008. [Google Scholar]
- Hauschild, A.; Montenbruck, O.; Sleewaegen, J.M.; Huisman, L.; Teunissen, P.J.G. Characterization of Compass M-1 signals. GPS Solut. 2012, 16, 117–126. [Google Scholar] [CrossRef]
- Montenbruck, O.; Steigenberger, P.; Hauschild, A. Multi-GNSS signal-in-space range error assessment—Methodology and results. Adv. Sp. Res. 2018, 61, 3020–3038. [Google Scholar] [CrossRef]
- Yang, Y.; Li, J.; Xu, J.; Tang, J.; Guo, H.; He, H. Contribution of the Compass satellite navigation system to global PNT users. Chin. Sci. Bull. 2011, 56, 2813–2819. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.; Li, J.; Wang, A.; Xu, J.; He, H.; Guo, H.; Shen, J.; Dai, X. Preliminary assessment of the navigation and positioning performance of BeiDou regional navigation satellite system. Sci. China Earth Sci. 2014, 57, 144–152. [Google Scholar] [CrossRef]
- Montenbruck, O.; Hauschild, A.; Steigenberger, P.; Hugentobler, U.; Teunissen, P.; Nakamura, S. Initial assessment of the COMPASS/BeiDou-2 regional navigation satellite system. GPS Solut. 2013, 17, 211–222. [Google Scholar] [CrossRef]
- Wang, G.; de Jong, K.; Zhao, Q.; Hu, Z.; Guo, J. Multipath analysis of code measurements for BeiDou geostationary satellites. GPS Solut. 2015, 19, 129–139. [Google Scholar] [CrossRef]
- Wanninger, L.; Beer, S. BeiDou satellite-induced code pseudorange variations: Diagnosis and therapy. GPS Solut. 2015, 19, 639–648. [Google Scholar] [CrossRef] [Green Version]
- Lou, Y.; Gong, X.; Gu, S.; Zheng, F.; Feng, Y. Assessment of code bias variations of BDS triple-frequency signals and their impacts on ambiguity resolution for long baselines. GPS Solut. 2017, 21, 177–186. [Google Scholar] [CrossRef]
- Montenbruck, O.; Steigenberger, P.; Hauschild, A. Broadcast versus precise ephemerides: A multi-GNSS perspective. GPS Solut. 2015, 19, 321–333. [Google Scholar] [CrossRef]
- Shi, C.; Zhao, Q.; Li, M. Precise orbit determination of Beidou satelliteswith precise positioning. Sci. China Earth Sci. 2012, 55, 1079–1086. [Google Scholar] [CrossRef]
- Steigenberger, P.; Hugentobler, U.; Hauschild, A.; Montenbruck, O. Orbit and clock analysis of compass GEO and IGSO satellites. J. Geod. 2013, 87, 515–525. [Google Scholar] [CrossRef]
- Zhao, Q.; Guo, J.; Li, M. Initial results of precise orbit and clock determination for COMPASS navigation satellite system. J. Geod. 2013, 87, 475–486. [Google Scholar] [CrossRef]
- Guo, F.; Li, X.; Zhang, X. Assessment of precise orbit and clock products for Galileo, BeiDou, and QZSS from IGS Multi-GNSS Experiment (MGEX). GPS Solut. 2016, 21, 279–290. [Google Scholar] [CrossRef]
- Guo, J.; Xu, X.; Zhao, Q. Precise orbit determination for quad-constellation satellites at Wuhan University: Strategy, result validation, and comparison. J. Geod. 2016, 90, 143–159. [Google Scholar] [CrossRef]
- Lou, Y.; Liu, Y.; Shi, C. Precise orbit determination of BeiDou constellation based on BETS and MGEX network. Sci. Rep. 2014, 4, 4692. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Ge, M.; Dai, X. Accuracy and reliability of multi-GNSS real-time precise positioning: GPS, GLONASS, BeiDou, and Galileo. J. Geod. 2015, 89, 607–635. [Google Scholar] [CrossRef]
- Geng, T.; Xie, X.; Zhao, Q. Improving BDS integer ambiguity resolution using satellite-induced code bias correction for precise orbit determination. GPS Solut. 2017, 21, 1191–1201. [Google Scholar] [CrossRef] [Green Version]
- Geng, J.; Li, X.; Zhao, Q.; Li, G. Inter-system PPP ambiguity resolution between GPS and Beidou for rapid initialization. J. Geod. 2018, 93, 383–398. [Google Scholar] [CrossRef]
- Li, P.; Zhang, X.; Guo, F. Ambiguity resolved precise point positioning with GPS and BeiDou. J. Geod. 2017, 91, 25–40. [Google Scholar]
- Pan, L.; Zhang, X.; Li, X.; Lu, X.; Liu, C.; Wang, Q. Satellite availability and point positioning accuracy evaluation on a global scale for integration of GPS, GLONASS, BeiDou and Galileo. Adv. Sp. Res. 2019, 63, 2696–2710. [Google Scholar] [CrossRef]
- Zhang, X.; Wu, M.; Liu, W.; Li, X.; Yu, S.; Lu, C.; Wickert, J. Initial assessment of the COMPASS/BeiDou-3: New-generation navigation signals. J. Geod. 2017, 91, 1225–1240. [Google Scholar] [CrossRef]
- Yang, Y.; Xu, Y.; Li, J.; Yang, C. Progress and performance evaluation of BeiDou global navigation satellite system: Data analysis based on BDS-3 demonstration system. Sci. China Earth Sci. 2018, 61, 614–624. [Google Scholar] [CrossRef]
- Tan, B.; Yuan, Y.; Wen, M.; Ning, Y.; Liu, X. Initial results of the precise orbit determination for the new-generation BeiDou satellites (BeiDou-3) based on the iGMAS Network. ISPRS Int. J. Geo-Inf. 2016, 5, 196. [Google Scholar] [CrossRef] [Green Version]
- Xie, X.; Geng, T.; Zhao, Q.; Cai, H.; Zhang, F.; Wang, X.; Meng, Y. Precise orbit determination for BDS-3 satellites using satellite-ground and inter-satellite link observations. GPS Solut. 2019, 23, 40. [Google Scholar] [CrossRef]
- Li, X.; Yuan, Y.; Zhu, Y.; Huang, J.; Wu, J.; Xiong, Y.; Zhang, X.; Li, X. Precise orbit determination for BDS3 experimental satellites using iGMAS and MGEX tracking networks. J. Geod. 2019, 93, 103–117. [Google Scholar] [CrossRef]
- Qu, L.; Du, M.; Wang, J.; Gao, Y.; Zhao, Q.; Zhang, Q.; Guo, X. Precise point positioning ambiguity resolution by integrating BDS-3e into BDS-2 and GPS. GPS Solut. 2019, 23, 63. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, B.; Nie, L.; Wei, C.; Jia, S.; Jiang, S. Initial assessment of BeiDou-3 global navigation satellite system: Signal quality, RTK and PPP. GPS Solut. 2019, 23, 111. [Google Scholar] [CrossRef]
- Gu, S.; Wang, Y.; Zhao, Q.; Zheng, F.; Gong, X. BDS-3 differential code bias estimation with undifferenced uncombined model based on triple-frequency observation. J. Geod. 2020, 94, 45. [Google Scholar] [CrossRef] [Green Version]
- Zhou, F.; Dong, D.; Li, P.; Li, X.; Schuh, H. Influence of stochastic modeling for inter-system biases on multi-GNSS undifferenced and uncombined precise point positioning. GPS Solut. 2019, 23, 59. [Google Scholar] [CrossRef]
- Geng, J.; Meng, X.; Dodson, A.H.; Teferle, F.N. Integer ambiguity resolution in precise point positioning: Method comparison. J. Geod. 2010, 84, 569–581. [Google Scholar] [CrossRef] [Green Version]
- Bock, H.; Dach, R.; Jaggi, A.; Beutler, G. High-rate GPS clock corrections from CODE: Support of 1 Hz applications. J. Geod. 2009, 83, 1083–1094. [Google Scholar] [CrossRef] [Green Version]
- Han, S.; Kwon, J.; Jekeli, C. Accurate absolute GPS positioning through satellite clock offset error estimation. J. Geod. 2001, 75, 33–43. [Google Scholar] [CrossRef]
- CSNO. Development of the BeiDou Navigation Satellite System (Version 3.0); China Satellite Navigation Office: Beijing, China, 2018. [Google Scholar]
- Zhou, F.; Cao, X.; Ge, Y.; Li, W. Assessment of the positioning performance and tropospheric delay retrieval with precise point positioning using products from different analysis centers. GPS Solut. 2020, 24, 12. [Google Scholar] [CrossRef]
- Ge, M.; Gendt, G.; Dick, G.; Zhang, F.P.; Rothacher, M. A New Data Processing Strategy for Huge GNSS Global Networks. J. Geod. 2006, 80, 199–203. [Google Scholar] [CrossRef]
- Li, X.; Li, X.; Yuan, Y.; Zhang, K.; Zhang, X.; Wickert, J. Multi-GNSS phase delay estimation and PPP ambiguity resolution: GPS, BDS, GLONASS, Galileo. J. Geod. 2018, 92, 579–608. [Google Scholar] [CrossRef]






















| Institution | ID | Observation Types | PCO/PCV | Interval | Availability |
|---|---|---|---|---|---|
| WHU | WUM0MGXFIN | B1I, B3I for BDS-2, and BDS-3 | igs14_2101.atx | SP3: 15 min CLK: 30 s | Since DOY 265, 2019 |
| GFZ | GBM0MGXRAP | SP3: 5 min CLK: 30 s/5 min | Since DOY 332, 2019 |
| Manufacturer | Receiver Types | Receiver Version | Supported BDS-3 Satellites |
|---|---|---|---|
| JAVAD | JAVAD TRE_3 | 3.7.6 | C19-C30, C32-C37 |
| JAVAD TRE_3 DELTA | 3.7.9 | C19-C30, C32-C46 | |
| SEPTENTRIO | SEPT ASTERX4 | 4.4.3 | C19-C30, C32-C37 |
| SEPT POLARX5 | 5.3.0 | C19-C20, C32-C37 | |
| 5.3.2 | |||
| SEPT PLOARX5TR | 5.3.2 | ||
| TRIMBLE | TRIMBLE ALLOY | 5.37 | C19-C30 |
| 5.43 | C19-C30, C32-C46 | ||
| 5.44 | |||
| TRIMBLE NETR9 | 5.37 | C19-C30 | |
| 5.42 | |||
| 5.43 | |||
| 5.44 |
| CEDU | JFNG | MCHL | MRO1 | NNOR | WTZZ | |
|---|---|---|---|---|---|---|
| mean | 2.89 | 2.09 | −4.84 | −0.29 | 1.87 | −1.23 |
| std | 0.06 | 0.08 | 0.08 | 0.06 | 0.06 | 0.07 |
| 15 min | 30 min | 1 h | 2 h | 6 h | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| CON | NO | CON | NO | CON | NO | CON | NO | CON | NO | ||
| CEDU | east | 15.4 | 17.0 | 6.7 | 6.8 | 4.1 | 3.9 | 2.8 | 2.7 | 0.5 | 0.5 |
| north | 3.1 | 3.1 | 1.9 | 1.9 | 1.2 | 1.3 | 0.8 | 0.9 | 0.6 | 0.6 | |
| up | 10.6 | 11.9 | 3.3 | 3.8 | 2.4 | 2.3 | 2.2 | 2.2 | 1.5 | 1.5 | |
| JFNG | east | 26.5 | 30.6 | 8.7 | 10.0 | 3.3 | 3.3 | 1.4 | 1.4 | 0.9 | 0.9 |
| north | 9.0 | 9.0 | 2.0 | 2.0 | 1.1 | 1.1 | 0.6 | 0.6 | 0.6 | 0.6 | |
| up | 47.9 | 44.5 | 7.3 | 7.1 | 4.1 | 3.9 | 3.2 | 3.1 | 2.4 | 2.3 | |
| MCHL | east | 23.2 | 25.3 | 10.0 | 10.4 | 3.7 | 3.7 | 3.6 | 3.6 | 0.6 | 0.7 |
| north | 6.4 | 7.3 | 2.3 | 2.5 | 1.5 | 1.6 | 1.1 | 1.1 | 0.4 | 0.4 | |
| up | 10.3 | 12.0 | 5.3 | 6.0 | 3.3 | 3.2 | 2.5 | 2.4 | 1.8 | 1.8 | |
| MRO1 | east | 19.6 | 19.2 | 5.5 | 5.4 | 2.6 | 2.6 | 1.6 | 1.6 | 0.5 | 0.5 |
| north | 7.1 | 6.9 | 1.8 | 1.7 | 1.0 | 1.0 | 0.6 | 0.6 | 0.4 | 0.4 | |
| up | 36.7 | 36.4 | 12.3 | 12.3 | 4.0 | 4.0 | 1.6 | 1.6 | 1.4 | 1.4 | |
| NNOR | east | 14.2 | 14.5 | 6.6 | 6.5 | 3.0 | 2.9 | 2.1 | 2.1 | 0.7 | 0.7 |
| north | 6.5 | 6.3 | 2.8 | 2.7 | 1.2 | 1.2 | 0.5 | 0.5 | 0.4 | 0.4 | |
| up | 16.0 | 17.4 | 5.9 | 6.1 | 3.8 | 3.7 | 1.7 | 1.7 | 2.1 | 2.1 | |
| WTZZ | east | 9.7 | 9.3 | 4.5 | 4.4 | 2.1 | 2.1 | 1.1 | 1.1 | 0.4 | 0.4 |
| north | 7.3 | 7.0 | 3.3 | 3.3 | 1.7 | 1.7 | 1.0 | 1.0 | 0.3 | 0.3 | |
| up | 16.8 | 17.0 | 6.7 | 6.7 | 2.5 | 2.5 | 1.6 | 1.6 | 1.5 | 1.5 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, W.; Chen, H.; Gao, Y.; Jiang, W.; Liu, X. Evaluation of Inter-System Bias between BDS-2 and BDS-3 Satellites and Its Impact on Precise Point Positioning. Remote Sens. 2020, 12, 2185. https://doi.org/10.3390/rs12142185
Zhao W, Chen H, Gao Y, Jiang W, Liu X. Evaluation of Inter-System Bias between BDS-2 and BDS-3 Satellites and Its Impact on Precise Point Positioning. Remote Sensing. 2020; 12(14):2185. https://doi.org/10.3390/rs12142185
Chicago/Turabian StyleZhao, Wen, Hua Chen, Yang Gao, Weiping Jiang, and Xuexi Liu. 2020. "Evaluation of Inter-System Bias between BDS-2 and BDS-3 Satellites and Its Impact on Precise Point Positioning" Remote Sensing 12, no. 14: 2185. https://doi.org/10.3390/rs12142185
APA StyleZhao, W., Chen, H., Gao, Y., Jiang, W., & Liu, X. (2020). Evaluation of Inter-System Bias between BDS-2 and BDS-3 Satellites and Its Impact on Precise Point Positioning. Remote Sensing, 12(14), 2185. https://doi.org/10.3390/rs12142185