Validation of the EGSIEM-REPRO GNSS Orbits and Satellite Clock Corrections
Abstract
:1. Introduction
2. Materials and Methods
2.1. Generation of GNSS Orbits
2.2. Generation of Gnss Clock Products
3. Results
3.1. ERP Misclosures
3.2. GNSS Satellite Clock Corrections Analysis
- GPS + GLONASS kinematic solution;
- GPS only kinematic solution;
- GLONASS only kinematic solution.
3.3. Validation of GNSS Orbits by Satellite Laser Ranging
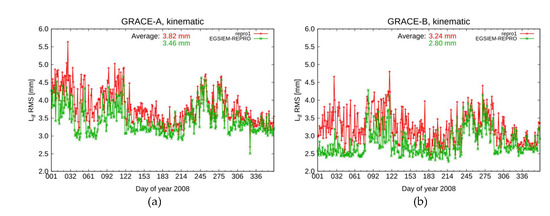
3.4. Quality Assessment Using GRACE Precise Orbit Determination
4. Discussion and Outlook
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Jäggi, A.; Weigelt, M.; Flechtner, F.; Güntner, A.; Mayer-Gürr, T.; Martinis, S.; Bruinsma, S.; Flury, J.; Bourgogne, S.; Steffen, H.; et al. European Gravity Service for Improved Emergency Management (EGSIEM)-from concept to implementation. Geophys. J. Int. 2019, 218, 1572–1590. [Google Scholar] [CrossRef]
- Tapley, B.; Bettadpur, S.; Ries, J.; Watkins, M. GRACE measurements of mass variability in the Earth system. Science 2004, 305, 503–505. [Google Scholar] [CrossRef] [Green Version]
- Jean, Y.; Meyer, U.; Jäggi, A. Combination of GRACE monthly gravity field solutions from different processing strategies. J. Geod. 2018, 92, 1313–1328. [Google Scholar] [CrossRef] [Green Version]
- Meyer, U.; Jean, Y.; Kvas, A.; Dahle, C.; Lemoine, J.-M.; Jäggi, A. Combination of GRACE monthly gravity fields on the normal equation level. J. Geod. 2019, 93, 1645–1658. [Google Scholar] [CrossRef] [Green Version]
- Zumberge, J.F.; Heflin, M.B.; Jefferson, D.C.; Watkins, M.M.; Webb, F.H. Precise point positioning for the efficient and robust analysis of GPS data from large networks. J. Geo. Res. 1997, 102, 5005–5017. [Google Scholar] [CrossRef] [Green Version]
- Dach, R.; Schaer, S.; Arnold, D.; Orliac, E.; Prange, L.; Sušnik, A.; Villiger, A.; Jäggi, A.; Beutler, G.; Brockmann, E.; et al. Center of Orbit Determination in Europe: IGS Technical Report 2017. In International GNSS Service: Technical Report 2017; Villiger, A., Dach, R., Eds.; (AIUB), IGS Central Bureau and University of Bern, Bern Open Publishing: Bern, Switzerland, 2018; pp. 32–44. [Google Scholar]
- Bock, H.; Beutler, G.; Schaer, S.; Springer, T.A.; Rothacher, M. Processing aspects related to permanent GPS arrays. Earth Planets Space 2000, 52, 657–662. [Google Scholar] [CrossRef] [Green Version]
- Bock, H.; Dach, R.; Jäggi, A.; Beutler, G. High-rate GPS clock corrections from CODE: Support of 1 Hz applications. J. Geod. 2009, 83, 1083–1094. [Google Scholar] [CrossRef] [Green Version]
- Beutler, G.; Rothacher, M.; Schaer, S.; Springer, T.A.; Kouba, J.; Neilan, R.E. The international GPS service (IGS): An interdisciplinary service in support of Earth sciences. Adv. Space Res. 1999, 23, 631–653. [Google Scholar] [CrossRef]
- Dow, J.; Neilan, R.; Rizos, C. The International GNSS service in a changing landscape of Global Navigational Satellite Systems. J. Geod. 2009, 82, 191–198. [Google Scholar] [CrossRef]
- Steigenberger, P.; Hugentobler, U.; Lutz, S.; Dach, R. CODE Contribution to the first IGS Reprocessing Campaign. Tech. Rep. 2011. 1/2011. Available online: http://www.bernese.unibe.ch/publist/2011/artproc/CODE_Repro1.pdf (accessed on 25 May 2020).
- Fritsche, M.; Sosnica, K.; Rodriguez-Solano, C.; Steigenberger, P.; Dietrich, R.; Dach, R.; Wang, K.; Hugentobler, U.; Rothacher, M. Homogeneous reprocessing of GPS, GLONASS and SLR observations. J. Geod. 2014, 88, 625–642. [Google Scholar] [CrossRef]
- Griffiths, J. Combined orbits and clocks from IGS 2nd reprocessing. J. Geod. 2018, 93, 177–195. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Altamimi, Z.; Rebischung, P.; Metivier, L.; Collilieux, X. ITRF2014: A new release of the International Terrestrial Reference Frame modeling nonlinear station motions. J. Geophys. Res. Solid Earth 2016, 121, 6109–6131. [Google Scholar] [CrossRef] [Green Version]
- Arnold, D.; Meindl, M.; Beutler, G.; Dach, R.; Schaer, S.; Lutz, S.; Prange, L.; Sosnica, K.; Mervart, L.; Jäggi, A. CODE’s new solar radiation pressure model for GNSS orbit determination. J. Geod. 2015, 89, 775–791. [Google Scholar] [CrossRef] [Green Version]
- Rebischung, P.; Griffiths, J.; Ray, J.; Schmid, R.; Collilieux, X.; Garayt, B. IGS08: The IGS realization of ITRF2008. GPS Solut. 2012, 16, 483–494. [Google Scholar] [CrossRef]
- Schmid, R.; Dach, R.; Collilieux, X.; Jäggi, A.; Schmitz, M.; Dilssner, F. Absolute IGS antenna phase center model igs08.atx: Status and potential improvements. J. Geod. 2016, 90, 343–364. [Google Scholar] [CrossRef] [Green Version]
- Dach, R.; Lutz, S.; Walser, P.; Fridez, P. (Eds.) The Bernese GNSS Software Version 5.2. User Manual; Astronomical Institute, University of Bern, Bern Open Publishing: Bern, Switzerland, 2015. [Google Scholar]
- The IGSMail Archives. Available online: https://lists.igs.org/pipermail/igsmail/2015/000869.html (accessed on 25 May 2020).
- Mervart, L.; Beutler, G.; Rothacher, M. Ambiguity resolution strategies using the results of the International GPS Geodynamics Service (IGS). Bull. Géodésique 1994, 68, 29–38. [Google Scholar] [CrossRef]
- Dach, R.; Schaer, S.; Lutz, S.; Meindl, A.; Bock, H.; Orliac, E.; Prange, L.; Thaller, D.; Mervart, L.; Jäggi, A.; et al. Center for Orbit Determination in Europe. IGS Technical Report 2011. In International GNSS Service: Technical Report 2011; Dach, R., Yean, Y., Eds.; IGS Central Bureau and University of Bern, Bern Open Publishing: Bern, Switzerland, 2012; pp. 21–34. [Google Scholar]
- Beutler, G.; Brockmann, E.; Hugentobler, U.; Mervart, L.; Rothacher, M.; Weber, R. Combining consecutive short arcs into long arcs for precise and efficient GPS orbit determination. J. Geod. 1996, 70, 287–299. [Google Scholar] [CrossRef]
- Caissy, M.; Agrotis, L.; Weber, G.; Hermandez-Pajares, M.; Hugentobler, U. The International GNSS Real-Time Service. GPS World 2012, 23, 52–58. [Google Scholar]
- Gurtner, W. RINEX: The receiver-independent exchange format. GPS World 1994, 5, 48–52. Available online: ftp://igs.org/pub/data/format/rinex2.txt (accessed on 15 May 2020).
- Lutz, S.; Meindl, M.; Steigenberger, P.; Beutler, G.; Sosnica, K.; Schaer, S.; Dach, R.; Arnold, D.; Thaller, D.; Jäggi, A. Impact of the arc length on GNSS analysis results. J. Geod. 2015, 90, 365–378. [Google Scholar] [CrossRef]
- Allan, D. Time and Frequency (Time-Domain) Characterization, Estimation, and Prediction of Precision Clocks and Oscillators. IEEE Trans. Ultrason. Ferroelectr. 1987, 34, 647–654. [Google Scholar] [CrossRef] [PubMed]
- Sosnica, K.; Thaller, D.; Dach, R.; Steigenberger, P.; Beutler, G.; Arnold, D.; Jäggi, A. Satellite laser ranging to GPS and GLONASS. J. Geod. 2015, 89, 725–743. [Google Scholar] [CrossRef] [Green Version]
- Rodriguez-Solano, C.; Hugentobler, U.; Steigenberger, P.; Blossfeld, M.; Fritsche, M. Reducing the draconitic errors in GNSS geodetic products. J. Geod. 2014, 88, 559–574. [Google Scholar] [CrossRef]
- Grahsl, A.; Sušnik, A.; Prange, L.; Arnold, D.; Dach, R.; Jäggi, A. GNSS orbit validation activites at the Astronomical Institute in Bern. In International Laser Ranging Service, Workshop 2016, 9–14 October 2016; Potsdam, Germany. Available online: https://cddis.nasa.gov/lw20/docs/2016/papers/P15-Maier_paper.pdf (accessed on 10 July 2020).
- Neubert, R.; Grunwaldt, L.; Neubert, J. The retroreflector for the CHAMP satellite: Final design and realization. In Proceedings of the 11th International Workshop on Laser Ranging, Deggendorf, Germany, 12–25 September 1998; pp. 260–270. [Google Scholar]
















| Empirical CODE Orbit Model (ECOM) | D | Y | B |
|---|---|---|---|
| D0B1 | constant | constant | constant, 1-cpr |
| D2B1 | constant, 2-cpr | constant | constant, 1-cpr |
| D4B1 | constant, 2-cpr, 4-cpr | constant | constant, 1-cpr |
| Solution | Periods (Days) | X | Y | ||
|---|---|---|---|---|---|
| R-02 | R-15 | R-02 | R-15 | ||
| 1-day | All | 194.2 | 174.9 | 255.7 | 240.2 |
| <30 | 138.1 | 137.2 | 173.7 | 183.8 | |
| 30 < P < 600 | 135.5 | 106.9 | 182.2 | 153.1 | |
| 3-day | All | 28.7 | 29.5 | 29.9 | 29.6 |
| <30 | 26.9 | 28 | 28.3 | 28.7 | |
| 30 < P < 600 | 9.1 | 8.1 | 9.0 | 7.1 | |
| Product Identifier | GRACE-A | GRACE-B |
|---|---|---|
| repro1 | 1.99 ± 18.14 (32,587) | 0.09 ± 18.51 (31,008) |
| EGSIEM-REPRO | 2.21 ± 12.93 (32,639) | 0.70 ± 14.14 (31,030) |
| Product Identifier | GRACE-A | GRACE-B |
|---|---|---|
| repro1 | 1.24 ± 19.98 (32,358) | 0.44 ± 23.00 (30,343) |
| EGSIEM-REPRO | 2.11 ± 17.00 (32,409) | 1.24 ± 19.75 (30,456) |
| Solution | Median (mm) | IQR (mm) |
|---|---|---|
| D0B1 | 5.0 | 38.0 |
| D2B1 | −2.4 | 32.8 |
| D4B1 | −2.6 | 33.3 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sušnik, A.; Grahsl, A.; Arnold, D.; Villiger, A.; Dach, R.; Beutler, G.; Jäggi, A. Validation of the EGSIEM-REPRO GNSS Orbits and Satellite Clock Corrections. Remote Sens. 2020, 12, 2322. https://doi.org/10.3390/rs12142322
Sušnik A, Grahsl A, Arnold D, Villiger A, Dach R, Beutler G, Jäggi A. Validation of the EGSIEM-REPRO GNSS Orbits and Satellite Clock Corrections. Remote Sensing. 2020; 12(14):2322. https://doi.org/10.3390/rs12142322
Chicago/Turabian StyleSušnik, Andreja, Andrea Grahsl, Daniel Arnold, Arturo Villiger, Rolf Dach, Gerhard Beutler, and Adrian Jäggi. 2020. "Validation of the EGSIEM-REPRO GNSS Orbits and Satellite Clock Corrections" Remote Sensing 12, no. 14: 2322. https://doi.org/10.3390/rs12142322
APA StyleSušnik, A., Grahsl, A., Arnold, D., Villiger, A., Dach, R., Beutler, G., & Jäggi, A. (2020). Validation of the EGSIEM-REPRO GNSS Orbits and Satellite Clock Corrections. Remote Sensing, 12(14), 2322. https://doi.org/10.3390/rs12142322