A Method to Detect and Track Moving Airplanes from a Satellite Video
Abstract
:1. Introduction
2. Background
3. Materials and Methods
3.1. Satellite Video Data and Preprocessing
3.2. Methods
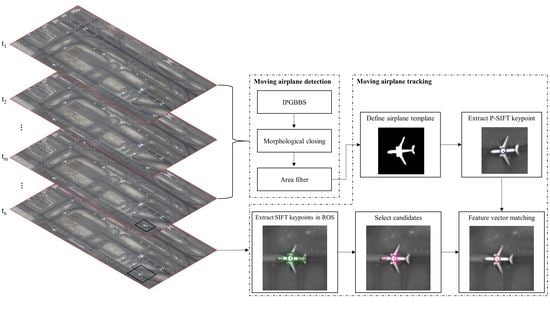
3.2.1. Moving Airplane Detection by IPGBBS
3.2.2. SIFT Based Keypoint and Feature Vector Extraction
3.2.3. Moving Airplane Tracking by P-SIFT Keypoint Matching
- High distinctiveness: The P-SIFT keypoint has the largest scale variable among all SIFT keypoint of the same airplane.
- High repeatability: For an airplane having a spectral contrast with its surrounding background, its P-SIFT keypoint can always be detected in any video frame.
- High stability of the feature vector: For an airplane with consistent spectral properties, the feature vector of its P-SIFT keypoint is highly rotation and scale invariant in the frame sequence.
3.3. Accuracy Assessment
4. Results
4.1. Results of Moving Airplane Detection
4.2. Results of Moving Airplane Tracking
5. Discussion
5.1. Computational Efficiency
5.2. Data Availability
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Shao, J.; Du, B.; Wu, C.; Zhang, L. Can we track targets from space? A hybrid kernel correlation filter tracker for satellite video. IEEE Trans. Geosci. Remote Sens. 2019, 57, 8719–8731. [Google Scholar] [CrossRef]
- Ahmadi, S.A.; Ghorbanian, A.; Mohammadzadeh, A. Moving vehicle detection, tracking and traffic parameter estimation from a satellite video: A perspective on a smarter city. Int. J. Remote Sens. 2019, 40, 8379–8394. [Google Scholar] [CrossRef]
- Mou, L.; Zhu, X.; Vakalopoulou, M.; Karantzalos, K.; Paragios, N.; Le Saux, B.; Moser, G.; Tuia, D. Multitemporal very high resolution from space: Outcome of the 2016 IEEE GRSS data fusion contest. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 3435–3447. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Jia, X.; Hu, J. Motion flow clustering for moving vehicle detection from satellite high definition video. In Proceedings of the International Conference on Digital Image Computing: Techniques and Applications (DICTA), Sydney, Australia, 29 November–1 December 2017; pp. 1–7. [Google Scholar]
- Yang, T.; Wang, X.; Yao, B.; Li, J.; Zhang, Y.; He, Z.; Duan, W. Small moving vehicle detection in a satellite video of an urban area. Sensors 2016, 16, 1528. [Google Scholar] [CrossRef] [Green Version]
- Mou, L.; Zhu, X. Spatiotemporal scene interpretation of space videos via deep neural network and tracklet analysis. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Bejing, China, 10–15 July 2016; pp. 1823–1826. [Google Scholar]
- Kopsiaftis, G.; Karantzalos, K. Vehicle detection and traffic density monitoring from very high resolution satellite video data. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 1881–1884. [Google Scholar]
- Vakalopoulou, M.; Platias, C.; Papadomanolaki, M.; Paragios, N.; Karantzalos, K. Simultaneous registration, segmentation and change detection from multisensor, multitemporal satellite image pairs. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Bejing, China, 10–15 July 2016; pp. 1827–1830. [Google Scholar] [CrossRef] [Green Version]
- Kelbe, D.; White, D.; Hardin, A.; Moehl, J.; Phillips, M. Sensor-agnostic photogrammetric image registration with applications to population modeling. Procedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Bejing, China, 10–15 July 2016; pp. 1831–1834. [Google Scholar] [CrossRef]
- Ahmadi, S.A.; Mohammadzadeh, A. A simple method for detecting and tracking vehicles and vessels from high resolution spaceborne videos. In Proceedings of the Joint Urban Remote Sensing Event (JURSE), Dubai, UAE, 6–8 March 2017; pp. 1–4. [Google Scholar] [CrossRef]
- Shao, J.; Du, B.; Wu, C.; Zhang, L. Tracking objects from satellite videos: A velocity feature based correlation filter. IEEE Trans. Geosci. Remote Sens. 2019, 57, 7860–7871. [Google Scholar] [CrossRef]
- Piccardi, M. Background subtraction techniques: A review. In Proceedings of the IEEE International Conference on Systems, Man and Cybernetics, The Hague, The Netherlands, 10–13 October 2004; Volume 4, pp. 3099–3104. [Google Scholar]
- Elhabian, S.Y.; El-Sayed, K.M.; Ahmed, S.H. Moving object detection in spatial domain using background removal techniques-state-of-art. Recent Patents Comput. Sci. 2008, 1, 32–54. [Google Scholar] [CrossRef]
- Chris, S.; Grimson, W.E. Adaptive background mixture models for real-time tracking. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Fort Collins, CO, USA, 23–25 June 1999; Volume 2, pp. 246–252. [Google Scholar] [CrossRef]
- Kim, K.; Chalidabhongse, T.H.; Harwood, D.; Davis, L. Real-time foreground-background segmentation using codebook model. Real-Time Imag. 2005, 11, 172–185. [Google Scholar] [CrossRef] [Green Version]
- Barnich, O.; Droogenbroeck, M. Van ViBe: A universal background subtraction algorithm for video sequences. IEEE Trans. Image Process 2010, 20, 1709–1724. [Google Scholar] [CrossRef] [Green Version]
- Barnich, O.; Van Droogenbroeck, M. ViBe: A powerful random technique to estimate the background in video sequences. In Proceedings of the 2009 IEEE International Conference on Acoustics, Speech and Signal Processing, Taipei, Taiwan, 19–24 April 2009; pp. 945–948. [Google Scholar]
- Koga, Y.; Miyazaki, H.; Shibasaki, R. A method for vehicle detection in high-resolution satellite images that uses a region-based object detector and unsupervised domain adaptation. Remote Sens. 2020, 12, 575. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Zhu, X. An efficient and scene-adaptive algorithm for vehicle detection in aerial images using an improved YOLOv3 framework. ISPRS Int. J. Geo-Inf. 2019, 8, 483. [Google Scholar] [CrossRef] [Green Version]
- Zheng, K.; Wei, M.; Sun, G.; Anas, B.; Li, Y. Using vehicle synthesis generative adversarial networks to improve vehicle detection in remote sensing images. ISPRS Int. J. Geo-Inf. 2019, 8, 390. [Google Scholar] [CrossRef] [Green Version]
- Audebert, N.; Le Saux, B.; Lefèvre, S. Segment-before-detect: Vehicle detection and classification through semantic segmentation of aerial images. Remote Sens. 2017, 9, 368. [Google Scholar] [CrossRef] [Green Version]
- Jain, S.D.; Xiong, B.; Grauman, K. FusionSeg: Learning to combine motion and appearance for fully automatic segmentation of generic objects in videos. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 2117–2126. [Google Scholar] [CrossRef]
- Perazzi, F.; Khoreva, A.; Benenson, R.; Schiele, B.; Sorkine-Hornung, A. Learning video object segmentation from static images. In Proceedings of the IEEE Conference on computer vision and pattern recognition, Honolulu, HI, USA, 22–25 July 2017; pp. 3491–3500. [Google Scholar]
- You, S.; Zhu, H.; Li, M.; Li, Y. A review of visual trackers and analysis of its application to mobile robot. arXiv 2019, arXiv:1910.09761. [Google Scholar]
- Pan, Z.; Liu, S.; Fu, W. A review of visual moving target tracking. Multimed. Tools Appl. 2017, 76, 16989–17018. [Google Scholar] [CrossRef]
- Lewis, J.P. Fast Normalized Cross-Correlation. 1995. Available online: https://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.21.6062 (accessed on 5 March 2020).
- Liwei, W.; Yan, Z.; Jufu, F. On the Euclidean distance of images. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 1334–1339. [Google Scholar] [CrossRef]
- Nakhmani, A.; Tannenbaum, A. A new distance measure based on generalized Image normalized cross-correlation for robust video tracking and image recognition. Pattern Recognit. Lett. 2013, 34, 315–321. [Google Scholar] [CrossRef] [Green Version]
- Tsai, D.-M.; Tsai, Y.-H. Rotation-invariant pattern matching with color ring-projection. Pattern Recognit. 2002, 35, 131–141. [Google Scholar] [CrossRef]
- Hu, M.K. Visual pattern recognition by moment invariants. IRE Trans. Inf. Theory 1962, 8, 179–187. [Google Scholar]
- Goshtasby, A. Template Matching in Rotated Images. IEEE Trans. Pattern Anal. Mach. Intell. 1985, 3, 338–344. [Google Scholar] [CrossRef]
- Kaur, A.; Singh, C. Automatic cephalometric landmark detection using Zernike moments and template matching. Signal Image Video Process. 2015, 9, 117–132. [Google Scholar] [CrossRef]
- Ullah, F.; Kaneko, S. Using orientation codes for rotation-invariant template matching. Pattern Recognit. 2004, 37, 201–209. [Google Scholar] [CrossRef]
- Choi, M.S.; Kim, W.Y. A novel two stage template matching method for rotation and illumination invariance. Pattern Recognit. 2002, 35, 119–129. [Google Scholar] [CrossRef]
- Wang, L.; Liu, T.; Wang, G.; Chan, K.L.; Yang, Q. Video tracking using learned hierarchical features. IEEE Trans. Image Process. 2015, 24, 1424–1435. [Google Scholar] [CrossRef] [PubMed]
- Choi, J.; Chang, H.J.; Fischer, T.; Yun, S.; Lee, K.; Jeong, J.; Demiris, Y.; Choi, J.Y. Context-aware deep feature compression for high-speed visual tracking. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 479–488. [Google Scholar] [CrossRef] [Green Version]
- Dicle, C.; Camps, O.I.; Sznaier, M. The way they move: Tracking multiple targets with similar appearance. In Proceedings of the IEEE International Conference on Computer Vision, Sidney, Australia, 1–8 December 2013; pp. 2304–2311. [Google Scholar] [CrossRef] [Green Version]
- Luo, W.; Xing, J.; Milan, A.; Zhang, X.; Liu, W.; Zhao, X.; Kim, T.-K. Multiple object tracking: A literature review. arXiv 2017, arXiv:1409.7618. [Google Scholar]
- Javed, O.; Shah, M.; Shafique, K. A hierarchical approach to robust background subtraction using color and gradient information. In Proceedings of the Workshop on Motion and Video Computing, Orlando, FL, USA, 9 December 2003. [Google Scholar] [CrossRef]
- Toyama, K.; Krumm, J.; Brumitt, B.; Meyers, B. Wallflower: Principles and practice of background maintenance. In Proceedings of the Seventh IEEE International Conference on Computer Vision, Kerkyra, Greece, 20–27 September 1999; pp. 255–261. [Google Scholar]
- Cristani, M.; Farenzena, M.; Bloisi, D.; Murino, V. Background subtraction for automated multisensor surveillance: A comprehensive review. EURASIP J. Adv. Signal. Process. 2010, 2010, 1–24. [Google Scholar] [CrossRef] [Green Version]
- Juan, L.; Gwon, L. A comparison of sift, pca-sift and surf. Int. J. Signal. Process. 2007, 8, 169–176. [Google Scholar] [CrossRef]
- Lowe, D.G. Distinctive Image Features from Scale-Invariant Keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]








| Parameter | Description | Value |
|---|---|---|
| σ0 | The initial standard deviation for the Gaussian background model | 30 |
| αb | The learning rate for adapting background pixels | 0.01 |
| αf | The learning rate for adapting foreground pixels | 0.001 |
| φ | The threshold to detect foreground pixels | 3 |
| Algorithm | FP Count | Recall | Precision | F1 Score |
|---|---|---|---|---|
| Initial Detection | ||||
| Codebook | 37 | 0.125 | 0.026 | 0.043 |
| MoG | 7866 | 1 | 0.001 | 0.002 |
| ViBe | 129 | 1 | 0.058 | 0.110 |
| IPGBBS | 34 | 1 | 0.191 | 0.321 |
| Boosted Detection | ||||
| Codebook | 1 | 0.125 | 0.500 | 0.200 |
| MoG | 199 | 0.750 | 0.029 | 0.056 |
| ViBe | 2 | 1.000 | 0.800 | 0.889 |
| IPGBBS | 1 | 1.000 | 0.890 | 0.942 |
| Airplane ID | Dynamic Speed (m/s) | Average Speed (m/s) | Total Distance (m) | ||||
|---|---|---|---|---|---|---|---|
| 17 s | 19 s | 21 s | 23 s | 25 s | |||
| 1 | 3.63 | 3.53 | 3.49 | 3.27 | 2.76 | 3.34 | 33.37 |
| 2 | 4.25 | 4.61 | 4.95 | 5.37 | 5.41 | 4.92 | 49.17 |
| 3 | 3.16 | 3.44 | 3.6 | 3.64 | 4.01 | 3.57 | 35.70 |
| 4 | 1 | 7.05 | 2.51 | 1.81 | 1.17 | 2.71 | 27.06 |
| 5 | 2.41 | 2.49 | 2.47 | 2.45 | 2.56 | 2.48 | 24.78 |
| 6 | 2.03 | 3.04 | 2.51 | 2.61 | 2.77 | 2.59 | 25.92 |
| 8 | 7.21 | 7.4 | 7.06 | 7.16 | 6.81 | 7.13 | 71.26 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, F.; Qiu, F.; Li, X.; Tang, Y.; Zhong, R.; Yang, C. A Method to Detect and Track Moving Airplanes from a Satellite Video. Remote Sens. 2020, 12, 2390. https://doi.org/10.3390/rs12152390
Shi F, Qiu F, Li X, Tang Y, Zhong R, Yang C. A Method to Detect and Track Moving Airplanes from a Satellite Video. Remote Sensing. 2020; 12(15):2390. https://doi.org/10.3390/rs12152390
Chicago/Turabian StyleShi, Fan, Fang Qiu, Xiao Li, Yunwei Tang, Ruofei Zhong, and Cankun Yang. 2020. "A Method to Detect and Track Moving Airplanes from a Satellite Video" Remote Sensing 12, no. 15: 2390. https://doi.org/10.3390/rs12152390
APA StyleShi, F., Qiu, F., Li, X., Tang, Y., Zhong, R., & Yang, C. (2020). A Method to Detect and Track Moving Airplanes from a Satellite Video. Remote Sensing, 12(15), 2390. https://doi.org/10.3390/rs12152390