Underwater 3D Rigid Object Tracking and 6-DOF Estimation: A Case Study of Giant Steel Pipe Scale Model Underwater Installation
Abstract
:1. Introduction
1.1. ETSP Underwater Installation
1.2. Related Work of 6-DOF Applications
1.3. Objectives and Challenges
2. ETSP Scale Model and Equipment
2.1. ETSP Scale Model and Coordinate System Definition
2.2. Imaging Equipment and Auxiliary Devices
2.3. Experiment Environment
2.4. Sample Images of ETSP Attitude Adjustment Simulation
3. Methodology
3.1. Camera Calibration
3.2. Motion Parameters Computation of 6-DOF
3.2.1. Multicamera Coordinate Transformation
3.2.2. Single-camera Relative Orientation Transformation
4. Results and Analysis
4.1. Results of Camera Calibration
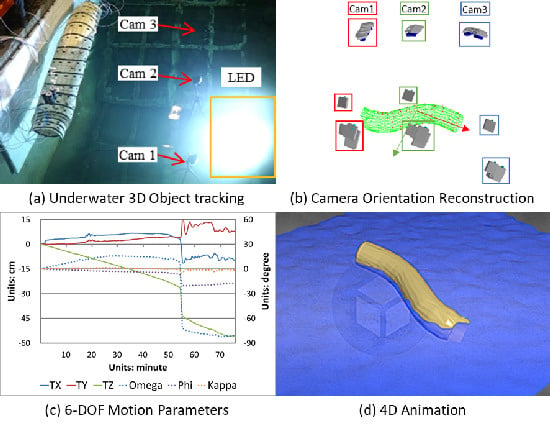
4.2. Motion Parameters and 4D Animation of ETSP
4.3. Comparison of Multi- and Single-Camera Approaches
5. Conclusions and Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Yu, Y.C.; Jou, B.J.D.; Hsu, H.H.; Cheng, C.T.; Chen, Y.M.; Lee, T.J. Typhoon Morakot meteorological analyses. J. Chin. Inst. Eng. 2013, 37, 595–610. [Google Scholar] [CrossRef]
- Li, H.C.; Hsieh, L.S.; Chen, L.C.; Lin, L.Y.; Li, W.S. Disaster investigation and analysis of Typhoon Morakot. J. Chin. Inst. Eng. 2013, 37, 558–569. [Google Scholar] [CrossRef]
- Chang, S.H.; Chen, C.S.; Wang, T.T. Sediment Sluice Tunnel of Zengwen Reservoir and construction of section with huge underground excavation adjacent to neighboring slope. Eng. Geol. 2019, 260, 105227. [Google Scholar] [CrossRef]
- Jhan, J.P.; Rau, J.Y.; Chou, C. 4D animation reconstruction from multi-camera coordinates transformation ISPRS—International archives of the photogrammetry. Remote Sens. Spat. Inf. Sci. 2016, 41, 841–847. [Google Scholar]
- Heller, V. Scale effects in physical hydraulic engineering models. J. Hydraul. Res. 2011, 49, 293–306. [Google Scholar] [CrossRef]
- Nistér, D.; Naroditsky, O.; Bergen, J. Visual odometry. In Proceedings of the 2004 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Washington, DC, USA, 27 June–2 July 2004; Volume 651, pp. 652–659. [Google Scholar]
- Scaramuzza, D.; Fraundorfer, F. Visual odometry [tutorial]. IEEE Robot. Autom. Mag. 2011, 18, 80–92. [Google Scholar] [CrossRef]
- Davison, A.J.; Reid, I.; Molton, N.D.; Stasse, O. MonoSLAM: Real-Time Single Camera SLAM. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 29, 1052–1067. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Luhmann, T. Close range photogrammetry for industrial applications. ISPRS J. Photogramm. Remote Sens. 2010, 65, 558–569. [Google Scholar] [CrossRef]
- Hartley, R.; Zisserman, A. Multiple View Geometry in Computer Vision; Cambridge University Press (CUP): New York, NY, USA, 2004. [Google Scholar]
- Lepetit, V.; Fua, P. Monocular model-based 3D tracking of rigid objects: A survey. Found. Trends® Comput. Graph. Vis. 2005, 1, 1–89. [Google Scholar] [CrossRef]
- Pollefeys, M.; Sinha, S.N.; Guan, L.; Franco, J.S. Multi-view calibration, synchronization, and dynamic scene reconstruction. In Multi-Camera Networks; Elsevier: Amsterdam, The Netherlands, 2009; pp. 29–75. [Google Scholar] [CrossRef]
- Rau, J.Y.; Yeh, P.C. A Semi-automatic image-based close range 3D modeling pipeline using a multi-camera configuration. Sensors 2012, 12, 11271–11293. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Poppe, R. Vision-based human motion analysis: An overview. Comput. Vis. Image Underst. 2007, 108, 4–18. [Google Scholar] [CrossRef]
- Nocerino, E.; Menna, F. Comparison between Single and Multi-Camera View Videogrammetry for Estimating 6DOF of a Rigid Body. SPIE Opt. Metrol. 2015, 9528, 1–14. [Google Scholar]
- Nocerino, E.; Menna, F.; Troisi, S. High accuracy low-cost videogrammetric system: An application to 6DOF estimation of ship models. SPIE Opt. Metrol. 2013, 8791, 87910J. [Google Scholar]
- Fryer, J.G.; Fraser, C.S. On the calibration of underwater cameras. Photogramm. Rec. 1986, 12, 73–85. [Google Scholar] [CrossRef]
- Telem, G.; Filin, S. Photogrammetric modeling of underwater environments. ISPRS J. Photogramm. Remote Sens. 2010, 65, 433–444. [Google Scholar] [CrossRef]
- Fraser, C.S.; Edmundson, K.L. Design and implementation of a computational processing system for off-line digital close-range photogrammetry. ISPRS J. Photogramm. Remote Sens. 2000, 55, 94–104. [Google Scholar] [CrossRef]
- Fraser, C.S. Digital camera self-calibration. ISPRS J. Photogramm. Remote Sens. 1997, 52, 149–159. [Google Scholar] [CrossRef]













| Specifications of ETSP | Prototype | 1:20 Scale Model | Scale Factor | |
|---|---|---|---|---|
| Length (m) | Curve | 60.00 | 3.00 | |
| Horizontal | 54.00 | 2.70 | ||
| Diameter (m) | Outer | 11.66 | 0.58 | |
| Inner | 10.00 | 0.50 | ||
| Weight (kg) | 1,576,000 | 197 | ||
| Volume (m3) | 4712.39 1/1694.13 2 | 0.59/0.21 | ||
| Density (g/cm3) | 0.33 1/0.93 2 | 0.33/0.93 | 1 | |
| Camera Info. | Air | Housing | UW |
|---|---|---|---|
| Focal length (mm) | 20.552 | 20.586 | 27.453 |
| Max. radial distortion (Pixels) | 166.03 | 155.93 | −168.33 |
| Max. decentering distortion (Pixels) | 16.67 | 13.74 | 16.31 |
| Sigma0 (Pixels) | 0.20 | 0.27 | 0.40 |
| Focal length ratio between UW and Housing | 1.333 | ||
| Differences between the Multi- and Single-Camera Approaches | ||||||
|---|---|---|---|---|---|---|
| Cases | RMSE of Translations (cm) | RMSE of Rotation Angles (degrees) | ||||
| ΔTX | ΔTY | ΔTZ | ΔO | ΔP | ΔK | |
| Cam1 | 0.15 | 1.11 | 1.28 | 0.35 | 0.03 | 0.05 |
| Cam2 | 0.14 | 1.12 | 1.29 | 0.41 | 0.03 | 0.05 |
| Cam3 | 0.15 | 1.11 | 1.28 | 0.36 | 0.02 | 0.05 |
| Differences between Each Single-Camera Approach | ||||||
| Cases | RMSE of Translations (cm) | RMSE of Rotation Angles (degrees) | ||||
| ΔTX | ΔTY | ΔTZ | ΔO | ΔP | ΔK | |
| Cam1 vs. Cam2 | 0.18 | 0.15 | 0.28 | 0.06 | 0.01 | 0.01 |
| Cam2 vs. Cam3 | 0.18 | 0.16 | 0.26 | 0.05 | 0.01 | 0.01 |
| Cam1 vs. Cam3 | 0.10 | 0.12 | 0.09 | 0.02 | 0.01 | 0.01 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jhan, J.-P.; Rau, J.-Y.; Chou, C.-M. Underwater 3D Rigid Object Tracking and 6-DOF Estimation: A Case Study of Giant Steel Pipe Scale Model Underwater Installation. Remote Sens. 2020, 12, 2600. https://doi.org/10.3390/rs12162600
Jhan J-P, Rau J-Y, Chou C-M. Underwater 3D Rigid Object Tracking and 6-DOF Estimation: A Case Study of Giant Steel Pipe Scale Model Underwater Installation. Remote Sensing. 2020; 12(16):2600. https://doi.org/10.3390/rs12162600
Chicago/Turabian StyleJhan, Jyun-Ping, Jiann-Yeou Rau, and Chih-Ming Chou. 2020. "Underwater 3D Rigid Object Tracking and 6-DOF Estimation: A Case Study of Giant Steel Pipe Scale Model Underwater Installation" Remote Sensing 12, no. 16: 2600. https://doi.org/10.3390/rs12162600
APA StyleJhan, J. -P., Rau, J. -Y., & Chou, C. -M. (2020). Underwater 3D Rigid Object Tracking and 6-DOF Estimation: A Case Study of Giant Steel Pipe Scale Model Underwater Installation. Remote Sensing, 12(16), 2600. https://doi.org/10.3390/rs12162600