Remote Sensing-Informed Zonation for Understanding Snow, Plant and Soil Moisture Dynamics within a Mountain Ecosystem
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Satellite Images
2.3. Supervised Learning for Snow Cover Classification
2.4. Unsupervised Learning for Time Series-based Zonation
2.5. Topographic Metrics
2.6. Soil Moisture
3. Results
3.1. Snow Classification
3.2. Time Lapse NDVI Images
3.3. Plant Dynamics-based Zonation
3.4. Relationship between Zonation and Topography, Plant Functional Types, Snow and Soil Moisture
4. Discussion
5. Conclusions
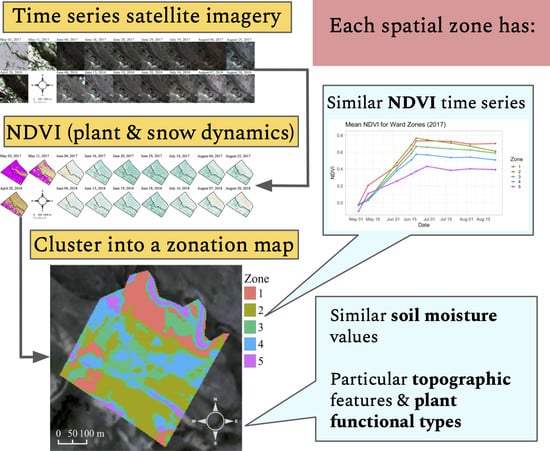
- The spatial zones—identified through hierarchical clustering of time series satellite imagery—are associated with distinct soil moisture distributions, plant functional types and topographic features.
- By comparing Ward and complete linkage methods of clustering, we found that the difference between the resulting zonation maps can be understood from the distance measures of these two linkages; the Ward method defined clusters with similar time series, which was more appropriate for our application, in contrast with the complete linkage method, which is more useful for extracting areas with extreme values.
- The zonation approach provides a tractable way to investigate ecosystem dynamics by structuring analysis and sampling efforts around spatial zones, where each zone represents a group with distinct plant-soil-snow interactions.
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lamanna, C.A. The Structure and Function of Subalpine Ecosystems in the Face of Climate Change. Ph.D. Thesis, University of Arizona, Tuscon, AZ, USA, 2012. [Google Scholar]
- Sloat, L.L.; Henderson, A.N.; Lamanna, C.; Enquist, B.J. The Effect of the Foresummer Drought on Carbon Exchange in Subalpine Meadows. Ecosystems 2015, 18, 533–545. [Google Scholar] [CrossRef]
- Wainwright, H.M.; Steefel, C.; Trutner, S.D.; Henderson, A.N.; Nikolopoulos, E.I.; Wilmer, C.F.; Chadwick, K.D.; Falco, N.; Schaettle, K.B.; Brown, J.B.; et al. Satellite-derived foresummer drought sensitivity of plant productivity in Rocky Mountain headwater catchments: Spatial heterogeneity and geological-geomorphological control. Environ. Res. Lett. 2020, 15, 084018. [Google Scholar] [CrossRef]
- Diffenbaugh, N.S.; Scherer, M.; Ashfaq, M. Response of snow-dependent hydrologic extremes to continued global warming. Nat. Clim. Chang. 2013, 3, 379–384. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gerten, D.; Schaphoff, S.; Haberlandt, U.; Lucht, W.; Sitch, S. Terrestrial vegetation and water balance—hydrological evaluation of a dynamic global vegetation model. J. Hydrol. 2004, 286, 249–270. [Google Scholar] [CrossRef]
- Fisher, J.B.; Malhi, Y.; Bonal, D.; Da Rocha, H.R.; De Araújo, A.C.; Gamo, M.; Goulden, M.L.; Hirano, T.; Huete, A.R.; Kondo, H.; et al. The land–atmosphere water flux in the tropics. Glob. Chang. Biol. 2009, 15, 2694–2714. [Google Scholar] [CrossRef]
- Engstrom, R.; Hope, A.; Kwon, H.; Stow, D.; Zamolodchikov, D. Spatial distribution of near surface soil moisture and its relationship to microtopography in the Alaskan Arctic coastal plain. Hydrol. Res. 2005, 36, 219–234. [Google Scholar] [CrossRef]
- Mohanty, B.P.; Skaggs, T.H.; Famiglietti, J.S. Analysis and mapping of field-scale soil moisture variability using high-resolution, ground-based data during the Southern Great Plains 1997 (SGP97) Hydrology Experiment. Water Resour. Res. 2000, 36, 1023–1031. [Google Scholar] [CrossRef] [Green Version]
- Vereecken, H.; Huisman, J.A.; Pachepsky, Y.; Montzka, C.; van der Kruk, J.; Bogena, H.; Weihermüller, L.; Herbst, M.; Martinez, G.; Vanderborght, J. On the spatio-temporal dynamics of soil moisture at the field scale. J. Hydrol. 2014, 516, 76–96. [Google Scholar] [CrossRef]
- Peng, J.; Loew, A.; Merlin, O.; Verhoest, N.E.C. A review of spatial downscaling of satellite remotely sensed soil moisture: Downscale Satellite-Based Soil Moisture. Rev. Geophys. 2017, 55, 341–366. [Google Scholar] [CrossRef]
- Anderson, M.; Neale, C.; Li, F.; Norman, J.; Kustas, W.; Jayanthi, H.; Chavez, J. Upscaling ground observations of vegetation water content, canopy height, and leaf area index during SMEX02 using aircraft and Landsat imagery. Remote Sens. Environ. 2004, 92, 447–464. [Google Scholar] [CrossRef]
- Wang, L.; Qu, J.J.; Hao, X.; Zhu, Q. Sensitivity studies of the moisture effects on MODIS SWIR reflectance and vegetation water indices. Int. J. Remote Sens. 2008, 29, 7065–7075. [Google Scholar] [CrossRef]
- Hubbard, S.S.; Gangodagamage, C.; Dafflon, B.; Wainwright, H.; Peterson, J.; Gusmeroli, A.; Ulrich, C.; Wu, Y.; Wilson, C.; Rowland, J.; et al. Quantifying and relating land-surface and subsurface variability in permafrost environments using LiDAR and surface geophysical datasets. Hydrogeol. J 2013, 21, 149–169. [Google Scholar] [CrossRef]
- Dafflon, B.; Oktem, R.; Peterson, J.; Ulrich, C.; Tran, A.P.; Romanovsky, V.; Hubbard, S.S. Coincident aboveground and belowground autonomous monitoring to quantify covariability in permafrost, soil, and vegetation properties in Arctic tundra. J. Geophys. Res. Biogeosci. 2017, 122, 1321–1342. [Google Scholar] [CrossRef] [Green Version]
- Falco, N.; Wainwright, H.; Dafflon, B.; Léger, E.; Peterson, J.; Steltzer, H.; Wilmer, C.; Rowland, J.C.; Williams, K.H.; Hubbard, S.S. Investigating Microtopographic and Soil Controls on a Mountainous Meadow Plant Community Using High-Resolution Remote Sensing and Surface Geophysical Data. J. Geophys. Res. Biogeosci. 2019, 124, 1618–1636. [Google Scholar] [CrossRef] [Green Version]
- Planet Team. Planet Application Program Interface: In Space for Life on Earth; Planet: San Francisco, CA, USA, 2017. [Google Scholar]
- Wainwright, H.M.; Dafflon, B.; Smith, L.J.; Hahn, M.S.; Curtis, J.B.; Wu, Y.; Ulrich, C.; Peterson, J.E.; Torn, M.S.; Hubbard, S.S. Identifying multiscale zonation and assessing the relative importance of polygon geomorphology on carbon fluxes in an Arctic tundra ecosystem. J. Geophys. Res. Biogeosci. 2015, 120, 788–808. [Google Scholar] [CrossRef]
- Dirmeyer, P.A.; Gao, X.; Zhao, M.; Guo, Z.; Oki, T.; Hanasaki, N. GSWP-2: Multimodel Analysis and Implications for Our Perception of the Land Surface. Bull. Am. Meteorol. Soc. 2006, 87, 1381–1398. [Google Scholar] [CrossRef] [Green Version]
- Koster, R.D.; Guo, Z.; Yang, R.; Dirmeyer, P.A.; Mitchell, K.; Puma, M.J. On the Nature of Soil Moisture in Land Surface Models. J. Clim. 2009, 22, 4322–4335. [Google Scholar] [CrossRef] [Green Version]
- Bergen, K.J.; Johnson, P.A.; de Hoop, M.V.; Beroza, G.C. Machine learning for data-driven discovery in solid Earth geoscience. Science 2019, 363, eaau0323. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 2nd ed.; Springer: New York, NY, USA, 2009; ISBN 978-0-387-84858-7. [Google Scholar]
- Reichstein, M.; Camps-Valls, G.; Stevens, B.; Jung, M.; Denzler, J.; Carvalhais, N. Prabhat Deep learning and process understanding for data-driven Earth system science. Nature 2019, 566, 195–204. [Google Scholar] [CrossRef]
- Duda, T.; Canty, M. Unsupervised classification of satellite imagery: Choosing a good algorithm. Int. J. Remote Sens. 2002, 23, 2193–2212. [Google Scholar] [CrossRef]
- Winkler, D.E.; Chapin, K.J.; Kueppers, L.M. Soil moisture mediates alpine life form and community productivity responses to warming. Ecology 2016, 97, 1553–1563. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hubbard, S.S.; Williams, K.H.; Agarwal, D.; Banfield, J.; Beller, H.; Bouskill, N.; Brodie, E.; Carroll, R.; Dafflon, B.; Dwivedi, D.; et al. The East River, Colorado, Watershed: A Mountainous Community Testbed for Improving Predictive Understanding of Multiscale Hydrological-Biogeochemical Dynamics. Vadose Zone J. 2018, 17, 180061. [Google Scholar] [CrossRef] [Green Version]
- Kittel, G.; Rondeau, R.; Kettler, S. A classification of the riparian vegetation of the Gunnison River Basin, Colorado. In Submitted to Colorado Department of Natural Resources and the Environmental Protection Agency. Prepared by Colorado Natural Heritage Program, Fort Collins; Colorado State University: Ft. Collins, CO, USA, 1995. [Google Scholar]
- PRISM Climate Group 30-Year Normals. Available online: https://prism.oregonstate.edu/normals/ (accessed on 4 July 2020).
- Tucker, C.J. Red and Photographic Infrared Linear Combinations for Monitoring Vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar] [CrossRef] [Green Version]
- Myneni, R.B.; Hall, F.G.; Sellers, P.J.; Marshak, A.L. The interpretation of spectral vegetation indexes. IEEE Trans. Geosci. Remote Sens. 1995, 33, 481–486. [Google Scholar] [CrossRef]
- Hall, D.K.; Riggs, G.A. Normalized-Difference Snow Index (NDSI). In Encyclopedia of Snow, Ice, and Glaciers; Singh, V.P., Singh, P., Haritashya, U.K., Eds.; Encyclopedia of Earth Sciences; Springer: Dordrecht, The Netherlands, 2011; ISBN 978-90-481-2642-2. [Google Scholar]
- Stillinger, T.; Roberts, D.A.; Collar, N.M.; Dozier, J. Cloud Masking for Landsat 8 and MODIS Terra Over Snow-Covered Terrain: Error Analysis and Spectral Similarity Between Snow and Cloud. Water Resour. Res. 2019, 55, 6169–6184. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, D.; Stow, D. The Effect of Training Strategies on Supervised Classification at Different Spatial Resolutions. Photogram. Eng. Remote Sens. 2002, 68, 1155–1162. [Google Scholar]
- Millard, K.; Richardson, M. On the Importance of Training Data Sample Selection in Random Forest Image Classification: A Case Study in Peatland Ecosystem Mapping. Remote Sens. 2015, 7, 8489–8515. [Google Scholar] [CrossRef] [Green Version]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Liaw, A.; Wiener, M. Classification and regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Kassambara, A. Practical Guide to Cluster Analysis in R: Unsupervised Machine Learning; Multivariate Analysis; STHDA: Paris, France, 2017; Volume 1, ISBN 978-1-5424-6270-9. [Google Scholar]
- Lawson, R.G.; Jurs, P.C. New index for clustering tendency and its application to chemical problems. J. Chem. Inf. Model. 1990, 30, 36–41. [Google Scholar] [CrossRef]
- Dormann, C.F.; Elith, J.; Bacher, S.; Buchmann, C.; Carl, G.; Carré, G.; Marquéz, J.R.G.; Gruber, B.; Lafourcade, B.; Leitão, P.J.; et al. Collinearity: A review of methods to deal with it and a simulation study evaluating their performance. Ecography 2013, 36, 27–46. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2019. [Google Scholar]
- Ward, J.H. Hierarchical Grouping to Optimize an Objective Function. J. Am. Stat. Assoc. 1963, 58, 236–244. [Google Scholar] [CrossRef]
- Wainwright, H.; Williams, K. LiDAR Collection in August 2015 over the East River Watershed, Colorado, USA; Lawrence Berkeley National Lab: Berkeley, CA, USA, 2017. [Google Scholar]
- Zevenbergen, L.W.; Thorne, C.R. Quantitative analysis of land surface topography. Earth Surf. Process. Landforms 1987, 12, 47–56. [Google Scholar] [CrossRef]
- Wilson, M.F.J.; O’Connell, B.; Brown, C.; Guinan, J.C.; Grehan, A.J. Multiscale Terrain Analysis of Multibeam Bathymetry Data for Habitat Mapping on the Continental Slope. Mar. Geod. 2007, 30, 3–35. [Google Scholar] [CrossRef] [Green Version]
- Quinn, P.F.; Beven, K.J.; Lamb, R. The in(a/tan/β) index: How to calculate it and how to use it within the topmodel framework. Hydrol. Process. 1995, 9, 161–182. [Google Scholar] [CrossRef]
- Falco, N.; Dafflon, B.; Devadoss, J.; Shirley, I.; Soom, F.; Uhlemann, S.; Wainwright, H.M. Time-domain reflectometer survey across the East River Watershed, Colorado. Watershed Funct. SFA 2020. [Google Scholar] [CrossRef]
- Jones, S.B.; Wraith, J.M.; Or, D. Time domain reflectometry measurement principles and applications. Hydrol. Process. 2002, 16, 141–153. [Google Scholar] [CrossRef]
- Dafflon, B.; Léger, E. Soil moisture and temperature data along the northeast facing hillslope at the Lower Montane site in the East River Watershed, Colorado. Watershed Funct. SFA 2020. [Google Scholar] [CrossRef]
- Dietz, A.J.; Kuenzer, C.; Gessner, U.; Dech, S. Remote sensing of snow—A review of available methods. Int. J. Remote Sens. 2012, 33, 4094–4134. [Google Scholar] [CrossRef]
- Chen, Y.; Wieder, W.R.; Hermes, A.L.; Hinckley, E.S. The role of physical properties in controlling soil nitrogen cycling across a tundra-forest ecotone of the Colorado Rocky Mountains, USA. CATENA 2020, 186, 104369. [Google Scholar] [CrossRef]
- Harte, J.; Saleska, S.R.; Levy, C. Convergent ecosystem responses to 23-year ambient and manipulated warming link advancing snowmelt and shrub encroachment to transient and long-term climate-soil carbon feedback. Glob. Chang. Biol. 2015, 21, 2349–2356. [Google Scholar] [CrossRef] [PubMed]
- Fisk, M.C.; Schmidt, S.K.; Seastedt, T.R. Topographic patterns of above- and belowground production and nitrogen cycling in alpine tundra. Ecology 1998, 79, 2253–2266. [Google Scholar] [CrossRef]
- Zhang, T.; Zhang, Y.; Xu, M.; Zhu, J.; Chen, N.; Jiang, Y.; Huang, K.; Zu, J.; Liu, Y.; Yu, G. Water availability is more important than temperature in driving the carbon fluxes of an alpine meadow on the Tibetan Plateau. Agric. For. Meteorol. 2018, 256–257, 22–31. [Google Scholar] [CrossRef]
- Walker, M.D.; Walker, D.A.; Theodose, T.A.; Webber, P.J. The Vegetation: Hierarchical Species-Environment Relationships. In Structure and Function of an Alpine Ecosystem: Niwot Ridge, Colorado; Bowman, W.D., Seastedt, T.R., Eds.; Oxford University Press: Oxford, UK, 2001; pp. 99–127. ISBN 978-0-19-511728-8. [Google Scholar]
- Litaor, M.I.; Williams, M.; Seastedt, T.R. Topographic controls on snow distribution, soil moisture, and species diversity of herbaceous alpine vegetation, Niwot Ridge, Colorado. J. Geophys. Res. 2008, 113, G2. [Google Scholar] [CrossRef] [Green Version]
- Körner, C. Alpine Plant Life: Functional Plant Ecology of High Mountain Ecosystems; Springer: Berlin, Germany, 2003; ISBN 978-3-540-00347-2. [Google Scholar]
- Oroza, C.A.; Zheng, Z.; Glaser, S.D.; Tuia, D.; Bales, R.C. Optimizing embedded sensor network design for catchment-scale snow-depth estimation using LiDAR and machine learning. Water Resour. Res. 2016, 52, 8174–8189. [Google Scholar] [CrossRef] [Green Version]
- Seddon, A.W.R.; Macias-Fauria, M.; Long, P.R.; Benz, D.; Willis, K.J. Sensitivity of global terrestrial ecosystems to climate variability. Nature 2016, 531, 229–232. [Google Scholar] [CrossRef] [Green Version]
- Dong, C.; MacDonald, G.M.; Willis, K.; Gillespie, T.W.; Okin, G.S.; Williams, A.P. Vegetation Responses to 2012–2016 Drought in Northern and Southern California. Geophys. Res. Lett. 2019, 46, 3810–3821. [Google Scholar] [CrossRef]












| Peak SWE (mm) | Peak SWE Date | Snowmelt Date | Mean June Temperature (°C) | |
|---|---|---|---|---|
| Historical Average | 391.2 | 10 April | 13 May | 11.4 |
| 2017 | 541.0 | 5 April | 28 May | 13.8 |
| 2018 | 256.5 | 9 April | 7 May | 14.1 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Devadoss, J.; Falco, N.; Dafflon, B.; Wu, Y.; Franklin, M.; Hermes, A.; Hinckley, E.-L.S.; Wainwright, H. Remote Sensing-Informed Zonation for Understanding Snow, Plant and Soil Moisture Dynamics within a Mountain Ecosystem. Remote Sens. 2020, 12, 2733. https://doi.org/10.3390/rs12172733
Devadoss J, Falco N, Dafflon B, Wu Y, Franklin M, Hermes A, Hinckley E-LS, Wainwright H. Remote Sensing-Informed Zonation for Understanding Snow, Plant and Soil Moisture Dynamics within a Mountain Ecosystem. Remote Sensing. 2020; 12(17):2733. https://doi.org/10.3390/rs12172733
Chicago/Turabian StyleDevadoss, Jashvina, Nicola Falco, Baptiste Dafflon, Yuxin Wu, Maya Franklin, Anna Hermes, Eve-Lyn S. Hinckley, and Haruko Wainwright. 2020. "Remote Sensing-Informed Zonation for Understanding Snow, Plant and Soil Moisture Dynamics within a Mountain Ecosystem" Remote Sensing 12, no. 17: 2733. https://doi.org/10.3390/rs12172733
APA StyleDevadoss, J., Falco, N., Dafflon, B., Wu, Y., Franklin, M., Hermes, A., Hinckley, E. -L. S., & Wainwright, H. (2020). Remote Sensing-Informed Zonation for Understanding Snow, Plant and Soil Moisture Dynamics within a Mountain Ecosystem. Remote Sensing, 12(17), 2733. https://doi.org/10.3390/rs12172733