Improved Point–Line Visual–Inertial Odometry System Using Helmert Variance Component Estimation

Abstract

Mobile platform visual image sequence inevitably has large areas with various types of weak textures, which affect the acquisition of accurate pose in the subsequent platform moving process. The visual–inertial odometry (VIO) with point features and line features as visual information shows a good performance in weak texture environments, which can solve these problems to a certain extent. However, the extraction and matching of line features are time consuming, and reasonable weights between the point and line features are hard to estimate, which makes it difficult to accurately track the pose of the platform in real time. In order to overcome the deficiency, an improved effective point–line visual–inertial odometry system is proposed in this paper, which makes use of geometric information of line features and combines with pixel correlation coefficient to match the line features. Furthermore, this system uses the Helmert variance component estimation method to adjust weights between point features and line features. Comprehensive experimental results on the two datasets of EuRoc MAV and PennCOSYVIO demonstrate that the point–line visual–inertial odometry system developed in this paper achieved significant improvements in both localization accuracy and efficiency compared with several state-of-the-art VIO systems.

1. Introduction

Simultaneous localization and mapping (SLAM) has become a key technology in autonomous driving and autonomous robot navigation, which has attracted widespread attention from academia and industry [1]. Visual SLAM technology, using an optical lens as a sensor, has the characteristics of low power consumption and small size, and is widely used in indoor environment positioning and navigation. However, visual SLAM has higher requirements for observation conditions. When the movement speed is fast or the illumination conditions are poor, the tracked point features are easily lost, resulting in larger positioning errors. In order to improve the reliability and accuracy of the visual SLAM system, fusing inertial navigation data into the visual SLAM system can significantly improve the positioning accuracy and reliability, which has become a research hotspot.

Visual–inertial odometry (VIO) uses visual and inertial navigation data for integrated navigation, which has broad application prospects and is studied worldwide [2,3]. The earliest VIO systems are mainly based on filtering technology [4,5] by using the integral of inertial measurement unit (IMU) measurement information to predict the state variables of the motion carrier, which further updates the state variables with visual information, so as to realize the tightly coupled approaches of vision and IMU information. However, with the linearization point of the nonlinear measurement model and the state transition model fixed in the filtering process, the linearization process may pose a large error with an unreasonable initial value. Thus, most scholars adopt the method of graph optimization [6,7] and use iterative methods to achieve higher precision parameter estimation [8]. For example, the OKVIS [9] system uses tightly coupled approaches to optimize the visual constraints of feature points and the preintegration constraints of IMU, and adopts optimization strategy based on keyframe and “first-in first-out” sliding window method by marginalizing the measurements from the oldest state. The VINS [10] system is a monocular visual–inertial SLAM scheme, which uses a sliding-window-based approach to construct the tightly coupled optimization of IMU preintegration and visual measurement information. In the sliding window, the oldest frame and the latest frame are selectively marginalized to maintain the optimized state variables and achieve a good optimization effect.

At present, mainstream VIO systems generally use point features as visual observations. For example, the VINS system is designed to detect Shi–Tomasi corner points [11], which uses the Kanade–Lucas–Tomasi (KLT) sparse optical flow method for tracking [12]. The S-MSCKF system [13] is designed to detect feature from accelerated segment test (FAST) corner points [14], using the KLT sparse optical flow [12] method for tracking. The OKVIS [9] system is designed to detect Harris [15] corner points, and uses binary robust invariant scalable keypoints (BRISK) [16] to match and track feature points. In most scenarios, the number of corner points are large and stable, which can ensure positioning performance. However, in weak texture environments and scenes where the illumination changes significantly, the point features always have less visual measurement information or have large measurement errors [17,18]. In order to present relief from the insufficient point feature performance, the line features that can provide structured information are introduced into the VIO system [19]. The simplest way is to use the two endpoints of the line to represent the 3D spatial line [20,21]. The 3D spatial line represented by the endpoints requires six parameters, while the 3D spatial line only has four degrees-of-freedom (DoFs); thus this representation will further cause a rank deficit problem of the equation and add additional computational burden. Bartoli and Sturm [22] proposed an orthogonal representation of line features by using four parameters to represent the 3D spatial line, in which the three-dimensional vector is related to the rotation of the line around three axes, and the last parameter represents the vertical distance from the origin to the spatial line [23]. This representation method has good numerical stability. Based on the line feature representation, He et al. [24] proposed a tightly coupled monocular point–line visual–inertial odometry (PL–VIO), which uses point and line measurement information and IMU measurement information to continuously estimate the state of the moving platform, and the state variables are optimized by the sliding window method, which ensures the accuracy and in the meantime guarantees an appropriate number of optimization variables, thereby improving the efficiency of optimization. Wen et al. [25] proposed a tightly coupled stereo point–line visual–inertial odometry (PLS–VIO), which uses stereo point–line features and IMU measurement information for tightly coupled optimization. Compared with the monocular VIO system, the stereo VIO system has higher stability and accuracy, while the time consumption is greatly increased.

In a VIO system that uses point features and line features at the same time, the traditional line feature matching method using line binary descriptors (LBD) [26] is time consuming, which reduces the real-time performance of the entire VIO system. At the same time, in the VIO system, it is difficult to provide reasonable and reliable weights of point and line features, and these two points are the key to getting good performance of the point–line coupled VIO system.

Line features have geometric information and good pixel level information. By using these two kinds of information, line features can be matched. Helmert variance component estimation (HVCE) [27] can determine the weights of different types of observations, and has been applied in many different fields including inertial navigation system (INS) and global navigation satellite system (GNSS) fusion positioning [28,29], global positioning system (GPS) and BeiDou navigation satellite system (BDS) pseudorange differential positioning [30], and other fields, which demonstrate the effectiveness of Helmert variance component estimation.

Based on this discussion, at the front end of the point–line VIO system, the line feature matching speed is slow; at the back end, when performing tightly coupled optimization of IMU observation, point feature observation, and line feature observation, it is difficult to determine a more reasonable point–line weight. Contributions described in this article follow:

• Aiming to solve the time-consuming problem of line feature matching, this paper comprehensively uses geometric information such as the position and angle of the line feature, as well as the pixel gray information around the line feature, and uses the correlation coefficient combined with the geometric information to match the line feature.
• Aiming to deal with the problem of difficulty in determining appropriate weights for line feature and point feature observations, this paper uses the Helmert variance component estimation (HVCE) method in the sliding window optimization based on the orthogonal representation of line features to assign more reasonable weights of point and line features.
• This article compares the improved point–line VIO system (IPL–VIO, improved PL–VIO) with OKVIS–Mono [9], VINS–Mono [10], PL–VIO [24] systems, and runs EuRoc MAV [31] and PennCOSYVIO [32] datasets. We comprehensively analyze the performance of the proposed method and other classic methods on different datasets.

The organization of this paper is as follows. After a comprehensive introduction in Section 1, the mathematical model is introduced in Section 2. The numerical experiments are conducted in Section 3 and the results are discussed in Section 4. Finally, conclusions and recommendations are given in Section 5.

2. Mathematical Formulation

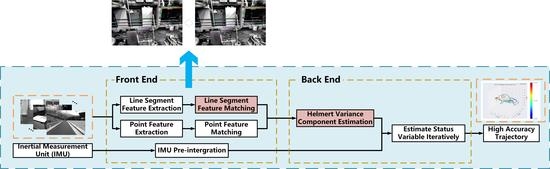
In general, the VIO system is divided into two modules: the front end and the back end. The front end is designed for the processing of visual measurement information, the preintegration of IMU measurement information [8], and calculates the initial poses. The back end is designed for data fusion and optimization. The front end of PL–VIO [24] adds line feature measurement information in addition to the original point feature measurement information, which improves the robustness of the algorithm. On the basis of PL–VIO, in order to reduce the front-end running time, the matching algorithm of the line feature is improved. In order to improve the accuracy of visual information in the overall optimization, we adopt the method of Helmert variance component estimation to better determine the prior weights of point and line information.

Figure 1 shows the algorithm pipeline. At the front end, we improved the line feature matching algorithm, as is shown in the red box. Simultaneously, as shown again in the red box at the back end, before entering the sliding window optimization, we use the Helmert variance component estimation algorithm to estimate the weights of point features and line features. Finally, we add visual information and IMU measurement information to the sliding window for optimization.

2.1. Notations

Figure 2 [24] shows the basic principle of the point–line coupled visual–inertial odometry, and stipulates the following notation. The visual–inertial odometry uses the extracted point features and line features as visual observation values, and couples IMU measurement information for integrated navigation; ${\mathrm{c}}_i$ and ${\mathrm{b}}_i$ represent camera frame and IMU body frame at time $t=i$; ${\mathrm{f}}_j$ and ${\mathrm{L}}_j$ represent a point feature and a line feature in the world coordinate system. The variable $z_{{\mathrm{f}}_j}^{{\mathrm{c}}_i}$ is the $j$th point feature observed by $i$th camera frame, $z_{{\mathrm{L}}_j}^{{\mathrm{c}}_i}$ is the $j$th line feature observed by $i$th camera frame; they compose visual observations, $z_{b_i{b}_j}$ represents a preintegrated IMU measurement between two keyframes; ${\mathrm{q}}_{bc}$ and ${\mathrm{p}}_{bc}$ are the extrinsic parameters between the camera frame and the body frame.

2.2. Improved Line Feature Matching Algorithm

In general, most line feature matching algorithms use LBD [26] to match line features, which need to describe the line features, and the matching of the descriptors would take a certain amount of time, hugely increasing the burden of calculations.

Since the line features contain rich geometric and texture characteristics, we comprehensively use the angle, position, and pixel properties of the line features to match the line features. The algorithm can increase the matching speed of the line features. The specific algorithm follows:

(1) According to the midpoint coordinates of the line features, narrow the matching range by extracting line features of the left and right image, and the two endpoints of the line features are extracted by the line segment detector (LSD) algorithm [33]. Then the left image is divided into m × n grids and the line features extracted from the left image are mapped into different grids according to the midpoint coordinates, as shown in Figure 3. When the midpoint coordinates of the line features in the right image fall into the corresponding grid of the left image, then all line features of the left image and the right image in the same grid are obtained as candidate line features. We denote candidate line features in the left image as $\{P_1,P_2,\dots P_n\}$ and in right image as $\{Q_1,Q_2,\dots Q_n\}$.

(2) According to the correlation coefficient of the pixels in the surrounding area of the line features, the matching line features are determined. We match the candidate line feature $P_i$ in $\{P_1,P_2,\dots P_n\}$ with the line features $\{Q_1,Q_2,\dots Q_n\}$, and the correlation coefficient of single pixel in the matching line is calculated using Formula (1) [34]. The respective correlation coefficients between $P_i$ and $\{Q_1,Q_2,\dots Q_n\}$ are calculated according to averaging the correlation coefficient of each pixel in the corresponding line features, and the correlation coefficients of the line features are sorted from small to large. If the correlation coefficient between $P_i$ and $Q_j$ is the largest, the respective correlation coefficients between $Q_j$ and $\{P_1,P_2,\dots P_n\}$ are calculated as well. If the correlation coefficient between $Q_j$ and $P_i$ is also the largest, $P_i$ and $Q_j$ are considered to be a pair of matching lines.

$$\rho (c,r,c^{\prime },r^{\prime })=\frac{{\displaystyle \sum _{i=1}^m{\displaystyle \sum _{j=1}^n{g}_{i+r,j+c}·g_{i+r^{\prime },j+c^{\prime }}^{\prime }-\frac{1}{m·n}\left({\displaystyle \sum _{i=1}^m{\displaystyle \sum _{j=1}^n{g}_{i+r,j+c}}}\right)}}\left({\displaystyle \sum _{i=1}^m{\displaystyle \sum _{j=1}^n{g}_{i+r^{\prime },j+c^{\prime }}^{\prime }}}\right)}{\sqrt{\left[{\displaystyle \sum _{i=1}^m{\displaystyle \sum _{j=1}^n{g}_{i+r,j+c}^2-\frac{1}{m·n}{\left({\displaystyle \sum _{i=1}^m{\displaystyle \sum _{j=1}^n{g}_{i+r,j+c}}}\right)}^2}}\right]\left[{\displaystyle \sum _{i=1}^m{\displaystyle \sum _{j=1}^n{g}_{i+r^{\prime },j+c^{\prime }}^{\prime }{}^2-\frac{1}{m·n}{\left({\displaystyle \sum _{i=1}^m{\displaystyle \sum _{j=1}^n{g}_{i+r^{\prime },j+c^{\prime }}^{\prime }}}\right)}^2}}\right]}}$$

(1)

where $c,r\in l_1$, $c^{\prime },r^{\prime }\in l_2$, $(c,r)$ are the pixel coordinates of line $l_1$ on left image; $(c^{\prime },r^{\prime })$ are the pixel coordinates of line $l_2$ on right image; $m,n$ are the matching window size; $g_{i,j}$ is the gray value at $(i,j)$ on left image; $g_{i,j}^{\prime }$ is the gray value at $(i,j)$ on right image; and $\rho (c,r,c^{\prime },r^{\prime })$ is the correlation coefficient.

(3) According to the rotation consistency of the line feature angles of the matched images, mismatches are eliminated. If the matching images are rotated, the angle changes of all matching line features should be consistent, which means the line feature rotation angles of the matching images have global consistency. If there is a rotation angle obviously inconsistent with the rotation angles of other matching line features, the matching pair may be seen as a mismatch and should be eliminated. This paper establishes a statistical histogram from 0 to 360 degrees in a unit of 1 degree. Through the histogram, the angle changes of matching line features are counted and the group with the largest number of histograms is retained. Line feature matching pairs that fall into other groups are considered to be mismatches and are eliminated.

2.3. Tightly Coupled VIO System

The VIO system in this paper uses point features, line features and IMU measurement information to optimize in the sliding window. In the optimization process, reasonable weights of different measurement information need to be given. Generally, the IMU measurements adopt the form of preintegration to construct the observation constraints, and the weight matrix of the IMU observation is recursively obtained, with the point features and the line features assigned prior weight matrices. Since the point feature and the line feature express different visual measurement information, the given prior weight matrices may be unreasonable to a certain extent. We use the Helmert variance component estimation method to obtain the post-test estimation of the prior weight matrices to better determine the contribution of visual measurement information to the overall optimization.

In order to better explain the improved algorithm in this article, the basic principles of tight coupling in the VIO system will be introduced in the following section, according to the basic principles of IMU error model, point feature error model, line feature error model, and Helmert variance component estimation.

2.3.1. Basic Principles of Tightly Coupled VIO System

In order to ensure accuracy and take into account efficiency at the same time, the sliding window algorithm is used to optimize state variables at the back end of the VIO system. Define the variable optimized in the sliding window at time $t$ as [24]:

$$\begin{array}{l}\mathit{X}=[{\mathit{x}}_n,{\mathit{x}}_{n+1},\dots ,{\mathit{x}}_{n+N},{\lambda }_m,{\lambda }_{m+1},\dots ,{\lambda }_{m+M},l_k,l_{k+1},\dots l_{k+K}]\\ {\mathit{x}}_i=[{\mathbf{p}}_{w{b}_i},{\mathbf{q}}_{w{b}_i},{\mathbf{v}}_i^w,{\mathbf{b}}_a^{b_i},{\mathbf{b}}_g^{b_i}]T,i\in [n,n+N]\end{array}$$

(2)

where ${\mathit{x}}_i$ describes the $i$th IMU body state; ${\mathbf{p}}_{w{b}_i}$, ${\mathbf{v}}_i^w$, ${\mathbf{q}}_{w{b}_i}$ describe the position, velocity, and orientation of the IMU body in the world frame; ${\mathbf{b}}_a^{b_i}$, ${\mathbf{b}}_g^{b_i}$ describe the acceleration bias and angular velocity bias. We only use one variable, the inverse depth ${\lambda }_k$, to parameterize the $k$th point landmark from its first observed keyframe. The variable $l_s$ is the orthonormal representation of the $s$th line feature in the world frame. Subscripts $n$, $m$, and $k$ are the start indexes of the body states, point landmarks, and line landmarks, respectively. $N$ is the number of keyframes in the sliding window. $M$ and $K$ are the numbers of point landmarks and line landmarks observed by all keyframes in the sliding window.

We optimize all the state variables in the sliding window by minimizing the sum of cost terms from all the measurement residuals [24]:

$$\begin{array}{ll}\min \rho ({\Vert {\mathbf{r}}_p-{\mathbf{J}}_p\mathit{X}\Vert }_{{\sum }_P}^2)+& {\displaystyle \sum _{i\in B}\rho ({\Vert {\mathbf{r}}_b({\mathit{z}}_{b_i{b}_{i+1}},\mathit{X})\Vert }_{{\sum }_{b_i{b}_{i+1}}}^2)}+\\ & {\displaystyle \sum _{(i,j)\in F}\rho ({\Vert {\mathbf{r}}_f({\mathit{z}}_{{\mathbf{f}}_j}^{c_i},\mathit{X})\Vert }_{{\sum }_{{\mathbf{f}}_j}^{c_i}}^2)}+{\displaystyle \sum _{(i,l)\in L}\rho ({\Vert {\mathbf{r}}_l({\mathit{z}}_{L_i}^{c_i},\mathit{X})\Vert }_{{\sum }_{L_i}^{c_i}}^2)}\end{array}$$

(3)

where $\{{\mathbf{r}}_p,{\mathbf{J}}_p\}$ is prior information after marginalizing out one frame in the sliding window, and ${\mathbf{J}}_p$ is the prior Jacobian matrix from the resulting Hessian matrix after the previous optimization. The variable ${\mathbf{r}}_b({\mathbf{z}}_{b_i{b}_{i+1}},\mathit{X})$ is an IMU measurement residual between the body state ${\mathit{x}}_i$ and ${\mathit{x}}_{i+1}$; $B$ is the set of all preintegrated IMU measurements in the sliding window; ${\mathbf{r}}_f(z_{{\mathbf{f}}_j}^{c_i},\mathit{X})$ and ${\mathbf{r}}_l(z_{L_i}^{c_i},\mathit{X})$ are the point feature reprojection residual and line feature reprojection residual, respectively. $F$ and $L$ are the sets of point features and line features observed by camera frames. The Cauchy robust function $\rho$ is used to suppress outliers.

We express the abovementioned nonlinear optimization process in the form of a factor graph [35]. As shown in Figure 4, the nodes represent the variables to be optimized; in the VIO system they are the visual features and the state variables of the IMU body. The edges represent the visual constraints, IMU preintegration constraints, and prior constraints. Through the constraint information of the edges, the state variables of the nodes are optimized.

2.3.2. IMU Measurement Model

The IMU original observation values are preintegrated between two consecutive camera observation frames of ${\mathbf{b}}_i$ and ${\mathbf{b}}_j$, and an IMU measurement error model constructed through the preintegration [24]:

$${\mathbf{r}}_b({\mathbf{z}}_{b_i{b}_j},\mathit{X})=\left[\begin{array}{c}\begin{array}{c}{\mathbf{r}}_p\\ {\mathbf{r}}_{\theta }\end{array}\\ {\mathbf{r}}_{\nu }\\ {\mathbf{r}}_{ba}\\ {\mathbf{r}}_{bg}\end{array}\right]={\left[\begin{array}{c}\begin{array}{c}{\mathbf{R}}_{b_{i}w}({\mathbf{p}}_{w{b}_j}-{\mathbf{p}}_{w{b}_i}-{\mathbf{v}}_i^w\Delta t+\frac{1}{2}{\mathbf{g}}^w\Delta t^2)-{\widehat{\mathsf{\alpha }}}_{b_i{b}_j}\\ 2{\left[{\widehat{\mathbf{q}}}_{b_j{b}_i}\otimes ({\mathbf{q}}_{b_{i}w}\otimes {\mathbf{q}}_{w{b}_j})\right]}_{xyz}\end{array}\\ {\mathbf{R}}_{b_{i}w}({\mathbf{v}}_j^w-v_i^w+{\mathbf{g}}^w\Delta t)-{\widehat{\mathsf{\beta }}}_{b_i{b}_j}\\ {\mathbf{b}}_a^{b_j}-{\mathbf{b}}_a^{b_i}\\ {\mathbf{b}}_g^{b_j}-{\mathbf{b}}_g^{b_i}\end{array}\right]}_{15\times 1}$$

(4)

where ${\mathbf{z}}_{b_i{b}_j}=[{\widehat{\mathsf{\alpha }}}_{b_i{b}_j},{\widehat{\mathsf{\beta }}}_{b_i{b}_j},{\widehat{\mathbf{q}}}_{b_i{b}_j}]$ is the preintegrated measurement value of the IMU [8]; ${[\mathbf{·}]}_{xyz}$ extracts the real part of a quaternion, which is used to approximate the three-dimensional rotation error.

2.3.3. Point Feature Measurement Model

For a point feature, the distance from the projection point to the observation point, that is, the reprojection error, is used to construct the point feature error model. The normalized image plane coordinate of the $k$th point on the $c_j$th frame is ${\mathit{z}}_{{\mathbf{f}}_k}^{c_j}={[u_{{\mathbf{f}}_k}^{c_j},v_{{\mathbf{f}}_k}^{c_j},1]}^T$, the reprojection error is defined as [24]:

$${\mathbf{r}}_f({\mathit{z}}_{{\mathbf{f}}_k}^{c_i},\mathit{X})=\left[\begin{array}{l}\frac{x^{c_j}}{z^{c_j}}-u_{{\mathbf{f}}_k}^{c_j}\\ \frac{y^{c_j}}{z^{c_j}}-v_{{\mathbf{f}}_k}^{c_j}\end{array}\right]$$

(5)

where ${\mathit{z}}_{{\mathbf{f}}_k}^{c_j}={[u_{{\mathbf{f}}_k}^{c_j},v_{{\mathbf{f}}_k}^{c_j},1]}^{\mathrm{T}}$ indicates the point on the normalized image plane that is observed by the camera frame $c_i$ and $[x^{c_j},y^{c_j},z^{c_j}]$ indicates the point transformed into the camera frame $c_i$.

2.3.4. Line Feature Measurement Model

The reprojection error of a line feature is defined as the distance from the endpoints to the projection line. For a pinhole model camera, a 3D spatial line $L=[\mathbf{n},\mathbf{d}{]}^{\mathrm{T}}$ is projected to the camera image plane by the following formula [24]:

$$\mathbf{l}=\left[\begin{array}{l}{l}_1\\ l_2\\ l_3\end{array}\right]={\rm K}{\mathbf{n}}^c=\left[\begin{array}{ccc}{f}_y& 0& 0\\ 0& f_x& 0\\ -f_y{c}_x& -f_x{c}_y& f_x{f}_y\end{array}\right]{\mathbf{n}}^c$$

(6)

where a 3D spatial line is represented by the normal vector $\mathbf{n}$ and the direction vector $\mathbf{d}$, ${\rm K}$ is the projection matrix for a line feature. According to the projection of a line (Equation (6)), the normal vector of a 3D spatial line is projected to the normalized plane, which is the projection line of a 3D spatial line.

The reprojection error of the line feature in camera frame $c_i$ is defined as (7) [24]:

$${\mathbf{r}}_l({\mathbf{z}}_{L_l}^{c_i},\mathit{X})=\left[\begin{array}{l}d({\mathbf{s}}_l^{c_i},{\mathbf{l}}_l^{c_i})\\ d({\mathbf{e}}_l^{c_i},{\mathbf{l}}_l^{c_i})\end{array}\right]$$

(7)

where $d(\mathbf{s},\mathbf{l})$ indicates the distance function from endpoint $\mathbf{s}$ to the projection line $\mathbf{l}$.

2.4. Basic Principle of Helmert Variance Component Estimation

Perform the first-order Taylor expansion of the point feature error formula (5) and the line feature error Formula (7) to obtain:

$${\mathbf{r}}_f({\mathit{z}}_{{\mathbf{f}}_k}^{c_i},\mathit{X})\approx {\mathbf{r}}_f({\mathit{z}}_{{\mathbf{f}}_k}^{c_i},{\mathit{X}}_0)+{\mathbf{J}}_f\Delta \mathrm{x}$$

(8)

$${\mathbf{r}}_l({\mathit{z}}_{L_l}^{c_i},\mathit{X})\approx {\mathbf{r}}_l({\mathit{z}}_{L_l}^{c_i},{\mathit{X}}_0)+{\mathbf{J}}_l\Delta \mathrm{x}$$

(9)

where ${\mathbf{r}}_f({\mathit{z}}_{{\mathbf{f}}_k}^{c_i},{\mathit{X}}_0)$ and ${\mathbf{r}}_l({\mathit{z}}_{L_l}^{c_i},{\mathit{X}}_0)$ are the values of the point feature error model and the line feature error model at the state variable ${\mathit{X}}_0$, respectively, ${\mathbf{J}}_f$ and ${\mathbf{J}}_l$ are the corresponding Jacobian matrices.

The constructed least squares optimization is:

$$\mathbf{H}\Delta \mathbf{x}=\mathbf{b}$$

(10)

$$\mathbf{H}={\mathbf{J}}_f^T{\mathbf{P}}_f{\mathbf{J}}_f+{\mathbf{J}}_l^T{\mathbf{P}}_l{\mathbf{J}}_l={\mathbf{H}}_f+{\mathbf{H}}_l$$

(11)

$$\mathbf{b}=-{\mathbf{J}}_f^T{\mathbf{P}}_f{\mathbf{r}}_f-{\mathbf{J}}_l^T{\mathbf{P}}_l{\mathbf{r}}_l={\mathbf{b}}_f+{\mathbf{b}}_l$$

(12)

where ${\mathbf{P}}_f$ and ${\mathbf{P}}_l$ are the weight matrices corresponding to the point feature observations and the line feature observations, respectively.

In general, during the first optimization, the weights of the point feature observations and the line feature observations are inappropriate, or the corresponding unit weight variances are not equal. Let the unit weight variance of the point feature and the line feature observations be ${\sigma }_f^2$, ${\sigma }_l^2$, the corresponding relationship between covariance matrix and the weight matrix is:

$${\mathbf{\Sigma }}_f={\sigma }_f^2{\mathbf{P}}_f^{-1}$$

(13)

$${\mathbf{\Sigma }}_l={\sigma }_l^2{\mathbf{P}}_l^{-1}$$

(14)

where ${\mathbf{\Sigma }}_f$ and ${\mathbf{\Sigma }}_l$ are the covariance matrices of the point and line features.

Using the rigorous formula of Helmert variance component estimation, we get:

$$\begin{array}{ll}E({\mathbf{r}}_f^T{\mathbf{P}}_f{\mathbf{r}}_f)& ={\sigma }_f^2\{\mathrm{tr}({\mathbf{H}}^{-1}{\mathbf{H}}_f{\mathbf{H}}^{-1}{\mathbf{H}}_f)-2\mathrm{tr}({\mathbf{H}}^{-1}{\mathbf{H}}_f)+{\mathrm{n}}_1\}\\ & +{\sigma }_l^{2}tr({\mathbf{H}}^{-1}{\mathbf{H}}_f{\mathbf{H}}^{-1}{\mathbf{H}}_l)\end{array}$$

(15)

$$\begin{array}{ll}E({\mathbf{r}}_l^T{\mathbf{P}}_l{\mathbf{r}}_l)=& {\sigma }_l^2\{\mathrm{tr}({\mathbf{H}}^{-1}{\mathbf{H}}_l{\mathbf{H}}^{-1}{\mathbf{H}}_l)-2\mathrm{tr}({\mathbf{H}}^{-1}{\mathbf{H}}_l)+{\mathrm{n}}_2\}\\ & +{\sigma }_f^{2}tr({\mathbf{H}}^{-1}{\mathbf{H}}_f{\mathbf{H}}^{-1}{\mathbf{H}}_l)\end{array}$$

(16)

where ${\mathrm{n}}_1$, ${\mathrm{n}}_2$ are the number of observations of point feature and line feature.

After combining the formulas we get:

$$\mathit{S}=\left[\begin{array}{cc}\mathrm{tr}({\mathbf{H}}^{-1}{\mathbf{H}}_f{\mathbf{H}}^{-1}{\mathbf{H}}_f)-2\mathrm{tr}({\mathbf{H}}^{-1}{\mathbf{H}}_f)+{\mathrm{n}}_1& \mathrm{tr}({\mathbf{H}}^{-1}{\mathbf{H}}_f{\mathbf{H}}^{-1}{\mathbf{H}}_l)\\ \mathrm{tr}({\mathbf{H}}^{-1}{\mathbf{H}}_f{\mathbf{H}}^{-1}{\mathbf{H}}_l)& \mathrm{tr}({\mathbf{H}}^{-1}{\mathbf{H}}_l{\mathbf{H}}^{-1}{\mathbf{H}}_l)-2\mathrm{tr}({\mathbf{H}}^{-1}{\mathbf{H}}_l)+{\mathrm{n}}_2\end{array}\right]$$

(17)

$$\mathit{W}=\left[\begin{array}{c}{\mathbf{r}}_f^T{\mathbf{P}}_f{\mathbf{r}}_f\\ {\mathbf{r}}_l^T{\mathbf{P}}_l{\mathbf{r}}_l\end{array}\right]\widehat{\mathit{\theta }}=\left[\begin{array}{c}{\widehat{\sigma }}_f^2\\ {\widehat{\sigma }}_l^2\end{array}\right]$$

(18)

$$\mathit{S}\widehat{\mathit{\theta }}=\mathit{W}$$

(19)

$$\widehat{\mathit{\theta }}={\mathit{S}}^{-1}\mathit{W}$$

(20)

We take the post-test unit weight variance ${\widehat{\sigma }}_f^2$ of the point feature as the unit weight variance, then the post-test weights of the point feature and the line feature are:

$${\widehat{\mathbf{P}}}_f={\mathbf{P}}_f$$

(21)

$${\widehat{\mathbf{P}}}_l=\frac{{\widehat{\sigma }}_f^2}{{\widehat{\sigma }}_l^2}{\mathbf{P}}_l$$

(22)

In sliding window optimization, in order to improve the efficiency of optimization, we ignore the trace part in the coefficient matrix $\mathit{S}$.

3. Experimental Results

We performed two improvements to the IPL–VIO system: the front-end line feature matching method and the back-end Helmert variance component estimation. In order to evaluate the performance of the algorithm in this paper, we used the EuRoc MAV [31] and PennCOSYVIO [32] datasets for verification.

We compared the IPL–VIO proposed in this paper with OKVIS–Mono [9], VINS–Mono [10], and PL–VIO [24] to verify the effectiveness of the method. OKVIS is a VIO system which can work with monocular or stereo modes. It uses a sliding window optimization algorithm to tightly couple visual point features and IMU measurements. VINS–Mono is a monocular visual inertial SLAM system that uses visual point features to assist in optimizing the IMU state. It uses a sliding window method for tightly coupling optimization and has closed-loop detection. PL–VIO is a monocular VIO system that uses a sliding window algorithm to tightly couple and optimize visual points, line features, and IMU measurement. Since the IPL–VIO in this article is a monocular VIO system, we compared it with the OKVIS in monocular mode and VINS–Mono without loop closure.

All the experiments were performed in the Ubuntu 16.04 system by an Intel Core i7-9750H CPU with 2.60 GHz and 8 GB RAM, on the ROS Kinetic [36].

3.1. Experimental Data Introduction

The EuRoc microaerial vehicle (MAV) datasets were collected by an MAV containing two scenes, a machine hall at ETH Zürich and an ordinary room, as shown in Figure 5. The datasets contain stereo images from a global shutter camera at 20 FPS and synchronized IMU measurements at 200 Hz [31]. Each dataset provides a groundtruth trajectory given by the VICON motion capture system. The datasets also provide all the extrinsic and intrinsic parameters. In our experiments, we only used the images from the left camera.

The PennCOSYVIO dataset contains images and synchronized IMU measurements that are collected with handheld equipment, including indoor and outdoor scenes of a glass building, as shown in Figure 5 [32]. Challenging factors include illumination changes, rapid rotations, and repetitive structures. The dataset also contains all the intrinsic and extrinsic parameters as well as the groundtruth trajectory.

We used the open source accuracy evaluation tool evo (https://michaelgrupp.github.io/evo/) to evaluate the accuracy of the EuRoc MAV datasets. We used absolute pose error (APE) as the error evaluation standard. For better comparison and analysis, we compared the rotation and translation parts of the trajectory and the groundtruth, respectively. Meanwhile, the tool provides a visualization of the comparison results, thereby the accuracy of the results can be analyzed more intuitively.

The PennCOSYVIO dataset is equipped with accuracy assessment tools (https://daniilidis-group.github.io/penncosyvio/). We used absolute pose error (APE) and relative pose error (RPE) as the evaluation criteria for errors. For RPE, it expresses the errors in percentages by dividing the value with the path length [32]. The creator of PennCOSYVIO cautiously selected the evaluation parameters, so their tool is suited for evaluating VIO approaches in this dataset. Therefore, we adopted this evaluation tool in our experiments.

3.2. Experimental Analysis of the Improved Line Feature Matching Algorithm

We compared the proposed line feature matching method with the LBD descriptor matching method. Figure 6 shows the line feature matching effect of the LBD descriptor matching method and the method proposed in this paper. Figure 7 shows the trajectory errors of two methods running on EuRoc MAV’s MH_02_easy dataset and V1_03_difficult dataset. We comprehensively used geometric information such as the position and angle of the line features, as well as the pixel gray information around the line feature to match the corresponding line feature. It can be seen that the accuracy of the improved algorithm is equivalent to the descriptor matching method.

We counted the trajectory error and time of the two methods after running the MH_02_easy and V1_03_difficult dataset of EuRoc MAV; the root mean square error (RMSE) of APE is used to evaluate the translation error and rotation error, respectively, and the time is the average time of the different algorithms running the datasets, as shown in

Table 1. Comparison of LBD descriptor matching method and the matching method we proposed.

Algorithm	Translation Error (m)		Rotation Error (°)		Time (ms)
	LBD	Proposed	LBD	Proposed	LBD	Proposed
MH_02_easy	0.13057	0.13253	1.73778	1.73950	74	15
V1_03_difficult	0.19490	0.19792	3.31055	3.27675	37	10

. It can be seen that running the MH_02_easy dataset by using the LBD descriptor matching algorithm, the errors of the translation part and rotation part are 0.13057 m and 1.73778 degrees; using the matching algorithm proposed in this article, the errors of the translation part and rotation part are 0.13253 m and 1.73950 degrees. Although the accuracy has decreased, it is very limited. When running the V1_03_difficult dataset, using the LBD descriptor matching algorithm to run the dataset, the errors of the translation part and rotation part are 0.19490 m and 3.31055 degrees; using the matching algorithm proposed in this paper, the errors of the translation part and rotation part are 0.19792 m and 3.27675 degrees. The accuracy of the translation part is slightly decreased, but the accuracy of the rotation part is slightly increased, and the overall accuracy is equivalent.

Using the improved line feature matching method and the LBD descriptor matching method, the final trajectory accuracy is equivalent. However, when comparing the running time for the MH_02_easy dataset, the LBD descriptor matching takes an average of 74 ms per frame, and the method described in this paper takes 15 ms; it can be seen that the running time is 20% that of the LBD descriptor matching method; for the V1_03_difficult dataset, LBD descriptor matching takes an average of 37 ms per frame, the method described in this paper takes 10 ms, and the running time is 27% of the LBD descriptor matching method. It can be seen that the method proposed in this article can effectively speed up the line feature matching.

3.3. Experimental Analysis of Helmert Variance Component Estimation

We ran OKVIS–Mono, VINS–Mono, PL–VIO and IPL–VIO systems on the EuRoc MAV datasets to evaluate the accuracy.

Table 2. The root mean square error (RMSE) results on several EuRoc MAV datasets.

Seq.	OKVIS–Mono		VINS–Mono		PL–VIO		IPL–VIO
	Trans (m)	Rot (°)	Trans (m)	Rot (°)	Trans (m)	Rot (°)	Trans (m)	Rot (°)
MH_02_easy	0.30655	3.92590	0.17143	2.30959	0.13057	1.74408	0.11534	1.47136
MH_03_medium	0.33372	3.30597	0.19401	1.64611	0.26095	1.70340	0.25248	1.96238
MH_04_difficult	0.38942	2.28610	0.34633	1.49141	0.35759	1.64553	0.36427	1.15279
MH_05_difficult	0.46736	2.37892	0.29151	0.71333	0.24446	1.07200	0.19262	1.25478
V1_01_easy	0.08982	5.83328	0.08683	6.33691	0.07792	5.82240	0.08778	5.85792
V1_03_difficult	0.27364	5.58748	0.20710	6.20628	0.19489	3.20856	0.18983	3.09684
V2_01_easy	0.13543	2.21792	0.08162	2.03056	0.08432	2.06150	0.07394	1.89420
V2_02_medium	0.19826	4.85181	0.15685	4.34073	0.14284	2.97881	0.11158	2.60868

shows the trajectories’ root mean square error (RMSE) of the translation part (m) and rotation part (degrees) of the four systems, the numbers in bold representing the estimated trajectory are more close to the groundtruth. Simultaneously, we made statistics of the histogram, which can be seen in Figure 8. As shown in Table 2, in terms of translation, the IPL–VIO system has higher accuracy than other systems on MH_02_easy, MH_05_difficult, V1_03_difficult, V2_01_easy, and V2_02_medium. In terms of rotation, the IPL–VIO system has higher accuracy on MH_02_easy, MH_04_difficult, V1_03_difficult, V2_01_easy, and V2_02_medium.

However, there are datasets in Table 2 whose accuracy decreases after the Helmert variance component method is used. As shown in Figure 9, in the V1_01_easy dataset, there are a large number of weak texture environments in the dataset scene, the quality of the extracted point features is relatively low. These still contain repetitive textures that make line features prone to the mismatch problem. Therefore, the RMSE of the translation part of PL–VIO is 0.07792 m and the RMSE of the rotation part is 5.82240 degrees. After using the Helmert variance component estimation, the results are susceptible to errors, resulting in a decrease in accuracy. The RMSE of the translation part of the IPL–VIO is 0.08778 m and the RMSE of the rotation part is 5.85792 degrees.

Another representative dataset is MH_03_medium. Compared with VINS–Mono, the accuracy of PL–VIO with added line features decreased. This is because in MH_03_medium, there are mismatches of line features, as shown in Figure 10; the line features in the scene are also relatively short and fragmented, which increase error. However, it can be seen from Table 2 that after Helmert variance component estimation, compared with PL–VIO, the accuracy of the translation part of IPL–VIO improved from 0.26095 to 0.25248 m.

In order to show a more intuitive result, we have drawn the trajectory estimation heat map of both PL–VIO and IPL–VIO in a same figure for the MH_05_difficult and V2_02_medium datasets. As shown in Figure 11 and Figure 12, the more reddish the figure, the larger the translation error of the trajectory. It can be seen that by adjusting the weights of the point and line features, the IPL–VIO has higher accuracy than PL–VIO.

When the carrier undergoes significant rotation changes or runs along straight lines, as shown in Figure 11a,b, using the Helmert variance component to estimate the weights of the points and lines, the trajectory accuracy can be significantly improved. From Figure 12a,b, we can see that for continuous rapid rotation changes, we can effectively improve the accuracy by adjusting the weights of point features and line features.

The PennCOSYVIO dataset contains various scenes such as obvious changes in lighting, rapid rotation, and repeated texture. For these challenges, the point and line features have different characteristics, so we used this dataset to compare and analyze the accuracy and time consumption of PL–VIO and IPL–VIO.

It can be seen from Figure 13 that the dataset contains a large number of repetitive linear textures and scenes with changes in light, illumination, and darkness, which can fully verify the method proposed in this article. We used the Helmert variance component estimation method to weight the two visual features, and the accuracy of the trajectory can be significantly improved. As shown in

Table 3. Absolute and relative pose error (APE and RPE) of the trajectory by running PL–VIO and IPL–VIO on the PennCOSYVIO dataset.

Algorithm	APE				RPE
	x (m)	y (m)	z (m)	rot (°)	x (%)	y (%)	z (%)	rot (°)
PL–VIO	0.406	0.169	1.006	2.3756	2.561	1.221	5.323	1.8276
IPL–VIO	0.371	0.137	0.911	2.2657	2.401	1.254	4.827	1.7983

, we compared APE and RPE of the trajectory after running PL–VIO and IPL–VIO. The rotation errors for the APE and RPE are expressed in degrees. The translation errors are expressed in the x, y, z axes, and the APE of translation part is expressed in meters, while the RPE of translation part is expressed in percentages. The numbers in bold, representing the estimated trajectory, are closer to the groundtruth. We can see that the trajectory accuracy has a significant improvement when compared to APE and RPE.

Table 4. The running time of each module of PL–VIO and IPL–VIO.

Module	Operation	Algorithm Times (ms)
		PL–VIO	IPL–VIO
front end	Point feature detection and matching	18	18
	Line feature detection and matching	74	60
	IMU forward propagation	1	1
back end	Nonlinear optimization	23	24

shows the time consumption of each module in IPL–VIO. It can be seen that for the average time per frame of line feature extraction and matching, the original method takes 74 ms; the method proposed in this article takes 60 ms. At the back end, without the Helmert variance component estimation method, it takes 23 ms, and using the Helmert variance component estimation method, it takes 24 ms. Thus, the time increase is negligible.

4. Discussion

In this paper, an improved point line coupled VIO system (IPL–VIO) was proposed. IPL–VIO has two main improvements. Firstly, geometric information such as the position and angle of the line feature and the gray information of the pixels around the line features were explored. We comprehensively used the geometric information and correlation coefficient to match the line features. Secondly, the Helmert variance component estimation method was introduced in the sliding window optimization, which ensured that more reasonable weights can be assigned for point features and line features. Compared with point features, line features are high-dimensional visual feature information that contain structured and geometric information, but matching line features is more time consuming. Thus, our proposed line feature matching method can shorten the matching time without any loss of accuracy. In addition, in the sliding window optimization, we used the Helmert variance component estimation method to determine more reasonable posterior weights for point features and line features, and improved the accuracy of visual information in the VIO system.

In order to verify the effectiveness of the proposed IPL–VIO system, a series of experiments were conducted. The improved line feature matching method was compared with the traditional LBD descriptor matching method, and the EuRoc MAV datasets were used for verification. As is shown, the improved matching method had the same accuracy as the traditional method, but reduced the running time to about a quarter of the traditional one. We compared and analyzed IPL–VIO with the current mainstream VIO systems: OKVIS–Mono, VINS–Mono, and PL–VIO. The test results on the EuRoc MAV datasets showed that the proposed IPL–VIO system performed well on most datasets when compared to other systems. There are also datasets with reduced accuracy, such as the V1_01_easy dataset, where there are a large number of weak texture and repetitive texture environments in the dataset scenes; the quality of point features and line features is both poor, after adjusting the weights, and the accuracy of the trajectory decreased. From the error heat map of the trajectory, it can be seen that the trajectory accuracy of IPL–VIO can be improved whether it is smooth running or exhibiting continuous large-angle rotation. We also compared and analyzed the proposed IPL–VIO system and the PL–VIO system on the PennCOSYVIO dataset, which contains challenging scenes such as significant changes in lighting, large-angle rotation, and repeated textures. It was seen that the IPL–VIO system can improve the final trajectory accuracy after readjusting the point-line weights with the Helmert variance component estimation method. Furthermore, we assessed the speed of each module of IPL–VIO and PL–VIO. The improved line feature matching method can reduce the time consumption of the front end, and the Helmert variance component estimation method added in the back end was effective for the back end; the increase load was quite limited and almost negligible, which proved the effectiveness of the proposed IPL–VIO system.

The algorithm in this paper improved the basis of PL–VIO. Therefore, in Table 2, Table 3 and Table 4, we indicate the results of a comprehensive comparison of PL–VIO and IPL–VIO. As is shown in Table 2, IPL–VIO had higher accuracy than PL–VIO in most datasets, which shows that the algorithm in this paper has better performance in different scenarios. As can be seen from Table 3, the error in the x, y, z three-axis direction of IPL–VIO was almost small compared with PL–VIO. It can be seen from Table 4 that the method proposed in this paper shortened the matching time of line features and leaves more time for the operation of other modules.

5. Conclusions

This paper proposes an improved point–line VIO system IPL–VIO. The IPL–VIO system has two main improvement modules: the front end and the back end. In the front-end module, an improved line feature matching algorithm is proposed, which comprehensively uses the geometric information and the pixel gray information of the line feature to match. In the back-end module, we use the Helmert variance component estimation method to determinate the weights of the point features and line features. We compared IPL–VIO with OKVIS–Mono [9], VINS–Mono [10], and PL–VIO [24], and verified the effectiveness of the algorithm on the EuRoc MAV [31] and PennCOSYVIO [32] datasets. According to the analysis and results, there are two further conclusions:

• Compared with traditional line feature matching methods using LBD descriptors, using geometric information and pixel gray information to match has the same accuracy as the traditional method, but reduces the running time to about a quarter of the traditional one.
• By using the Helmert variance component estimation method to determine more reasonable posterior weights for point features and line features, this method can improve the accuracy of visual information in the VIO system. The final trajectory accuracy is improved and time consumption is almost negligible.

We also look forward to the next work. At the back end, we use the simplified formula of the Helmert variance component estimation method, which introduces a certain degree of error. In the future, we would like to study how to improve the accuracy of weight determination without increasing the back-end overhead. We only use the Helmert variance component estimation method to estimate the weights of visual features; in the future, we will try to figure out how to better determine the weights of visual information and IMU information.