Hyperspectral Image Classification Using Feature Relations Map Learning
Abstract
:1. Introduction
2. Methods
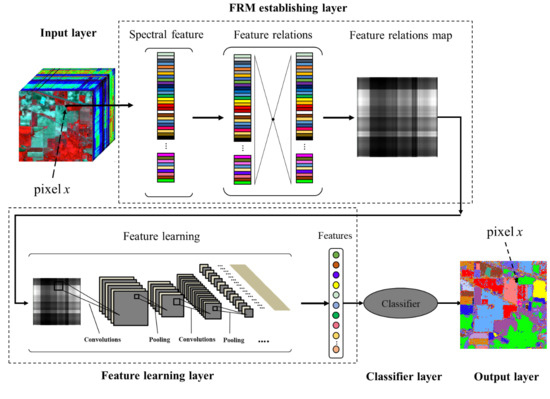
2.1. Feature Relations Map Learning
2.1.1. Feature Relations Map Establishment
2.1.2. Feature Learning Method
2.1.3. Classification Method
2.2. Measurement of the Feature Relations Map Difference
2.3. Measurement of the Separability of Different Class Samples
2.4. Accuracy Verification
3. Dataset Descriptions and Experimental Designs
4. Experimental Results and Analysis
4.1. Feature Relations Map Analysis
4.1.1. Feature Relations Map Results
4.1.2. Feature Relations Map Differences
4.2. Sample Separability with Features Learned from SFRMs
4.3. Classification Results and Analysis
4.3.1. Classification Performance at the Overall Level
4.3.2. Classification Performance at the Per-Class Level
4.3.3. Impact of the Training Sample Size on FRML
4.3.4. Land Use Mapping with FRML
4.3.5. Time Cost
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Mou, L.; Ghamisi, P.; Zhu, X.X. Deep Recurrent Neural Networks for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote. Sens. 2017, 55, 3639–3655. [Google Scholar] [CrossRef] [Green Version]
- Kong, F.; Wen, K.; Li, Y. Regularized Multiple Sparse Bayesian Learning for Hyperspectral Target Detection. J. Geovis. Spat. Anal. 2019, 3. [Google Scholar] [CrossRef]
- Bansod, B.; Singh, R.; Thakur, R. Analysis of water quality parameters by hyperspectral imaging in Ganges River. Spat. Inf. Res. 2018, 26, 203–211. [Google Scholar] [CrossRef]
- Caballero, D.; Calvini, R.; Amigo, J.M. Hyperspectral imaging in crop fields: Precision agriculture. In Design and Optimization in Organic Synthesis; Elsevier BV: Amsterdam, The Netherlands, 2020; Volume 32, pp. 453–473. [Google Scholar]
- Yokoya, N.; Chan, J.C.-W.; Segl, K. Potential of Resolution-Enhanced Hyperspectral Data for Mineral Mapping Using Simulated EnMAP and Sentinel-2 Images. Remote. Sens. 2016, 8, 172. [Google Scholar] [CrossRef] [Green Version]
- Audebert, N.; Le Saux, B.; Lefèvre, S. Deep Learning for Classification of Hyperspectral Data: A Comparative Review. IEEE Geosci. Remote. Sens. Mag. 2019, 7, 159–173. [Google Scholar] [CrossRef] [Green Version]
- Li, S.; Song, W.; Fang, L.; Chen, Y.; Ghamisi, P.; Benediktsson, J.A. Deep Learning for Hyperspectral Image Classification: An Overview. IEEE Trans. Geosci. Remote. Sens. 2019, 57, 6690–6709. [Google Scholar] [CrossRef] [Green Version]
- Xia, J.; Yokoya, N.; Iwasaki, A. Hyperspectral Image Classification with Canonical Correlation Forests. IEEE Trans. Geosci. Remote. Sens. 2016, 55, 421–431. [Google Scholar] [CrossRef]
- Yang, D.; Bao, W. Group Lasso-Based Band Selection for Hyperspectral Image Classification. IEEE Geosci. Remote. Sens. Lett. 2017, 14, 2438–2442. [Google Scholar] [CrossRef]
- Khan, M.J.; Khan, H.S.; Yousaf, A.; Khurshid, K.; Abbas, A. Modern Trends in Hyperspectral Image Analysis: A Review. IEEE Access 2018, 6, 14118–14129. [Google Scholar] [CrossRef]
- Du, P.; Bai, X.; Tan, K.; Xue, Z.; Samat, A.; Xia, J.; Li, E.; Su, H.; Liu, W. Advances of Four Machine Learning Methods for Spatial Data Handling: A Review. J. Geovis. Spat. Anal. 2020, 4, 1–25. [Google Scholar] [CrossRef]
- Chan, J.C.-W.; Paelinckx, D. Evaluation of Random Forest and Adaboost tree-based ensemble classification and spectral band selection for ecotope mapping using airborne hyperspectral imagery. Remote. Sens. Environ. 2008, 112, 2999–3011. [Google Scholar] [CrossRef]
- Cao, X.; Wen, L.; Ge, Y.; Zhao, J.; Jiao, L. Rotation-Based Deep Forest for Hyperspectral Imagery Classification. IEEE Geosci. Remote. Sens. Lett. 2019, 16, 1105–1109. [Google Scholar] [CrossRef]
- Zhang, Y.; Cao, G.; Li, X.; Wang, B. Cascaded Random Forest for Hyperspectral Image Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote. Sens. 2018, 11, 1082–1094. [Google Scholar] [CrossRef]
- Ergul, U.; Bilgin, G. HCKBoost: Hybridized composite kernel boosting with extreme learning machines for hyperspectral image classification. Neurocomputing 2019, 334, 100–113. [Google Scholar] [CrossRef]
- Su, H.; Yu, Y.; Du, Q.; Du, P. Ensemble Learning for Hyperspectral Image Classification Using Tangent Collaborative Representation. IEEE Trans. Geosci. Remote. Sens. 2020, 58, 3778–3790. [Google Scholar] [CrossRef]
- Datta, A.; Ghosh, S.; Ghosh, A. Unsupervised band extraction for hyperspectral images using clustering and kernel principal component analysis. Int. J. Remote. Sens. 2017, 38, 850–873. [Google Scholar] [CrossRef]
- Jia, S.; Deng, X.; Zhu, J.; Xu, M.; Zhou, J.; Jia, X. Collaborative Representation-Based Multiscale Superpixel Fusion for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote. Sens. 2019, 57, 7770–7784. [Google Scholar] [CrossRef]
- Mahdianpari, M.; Salehi, B.; Mohammadimanesh, F.; Brisco, B.; Mahdavi, S.; Amani, M.; Granger, J.E. Fisher Linear Discriminant Analysis of coherency matrix for wetland classification using PolSAR imagery. Remote. Sens. Environ. 2018, 206, 300–317. [Google Scholar] [CrossRef]
- Ghamisi, P.; Souza, R.; Benediktsson, J.A.; Rittner, L.; Lotufo, R.D.A.; Zhu, X.X. Hyperspectral Data Classification Using Extended Extinction Profiles. IEEE Geosci. Remote. Sens. Lett. 2016, 13, 1641–1645. [Google Scholar] [CrossRef] [Green Version]
- Majdar, R.S.; Ghassemian, H. A probabilistic SVM approach for hyperspectral image classification using spectral and texture features. Int. J. Remote. Sens. 2017, 38, 4265–4284. [Google Scholar] [CrossRef]
- Jia, S.; Hu, J.; Zhu, J.; Jia, X.; Li, Q. Three-Dimensional Local Binary Patterns for Hyperspectral Imagery Classification. IEEE Trans. Geosci. Remote. Sens. 2017, 55, 2399–2413. [Google Scholar] [CrossRef]
- He, L.; Li, J.; Liu, C.; Li, S. Recent Advances on Spectral–Spatial Hyperspectral Image Classification: An Overview and New Guidelines. IEEE Trans. Geosci. Remote. Sens. 2018, 56, 1579–1597. [Google Scholar] [CrossRef]
- Zhu, X.X.; Tuia, D.; Mou, L.; Xia, G.-S.; Zhang, L.; Xu, F.; Fraundorfer, F. Deep Learning in Remote Sensing: A Comprehensive Review and List of Resources. IEEE Geosci. Remote. Sens. Mag. 2017, 5, 8–36. [Google Scholar] [CrossRef] [Green Version]
- Cheng, G.; Yang, C.; Yao, X.; Guo, L.; Han, J. When Deep Learning Meets Metric Learning: Remote Sensing Image Scene Classification via Learning Discriminative CNNs. IEEE Trans. Geosci. Remote. Sens. 2018, 56, 2811–2821. [Google Scholar] [CrossRef]
- Zhong, Y.; Fei, F.; Liu, Y.; Zhao, B.; Jiao, H.; Zhang, L. SatCNN: Satellite image dataset classification using agile convolutional neural networks. Remote. Sens. Lett. 2016, 8, 136–145. [Google Scholar] [CrossRef]
- Paoletti, M.E.; Haut, J.M.; Plaza, J.; Plaza, J. A new deep convolutional neural network for fast hyperspectral image classification. ISPRS J. Photogramm. Remote. Sens. 2018, 145, 120–147. [Google Scholar] [CrossRef]
- Santara, A.; Mani, K.; Hatwar, P.; Singh, A.; Garg, A.; Padia, K.; Mitra, P. BASS Net: Band-Adaptive Spectral-Spatial Feature Learning Neural Network for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote. Sens. 2017, 55, 5293–5301. [Google Scholar] [CrossRef] [Green Version]
- Ghamisi, P.; Plaza, J.; Chen, Y.; Li, J.; Plaza, J. Advanced Spectral Classifiers for Hyperspectral Images: A review. IEEE Geosci. Remote. Sens. Mag. 2017, 5, 8–32. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Zhu, L.; Ghamisi, P.; Jia, X.; Li, G.; Tang, L. Hyperspectral Images Classification with Gabor Filtering and Convolutional Neural Network. IEEE Geosci. Remote. Sens. Lett. 2017, 14, 2355–2359. [Google Scholar] [CrossRef]
- Pan, B.; Shi, Z.; Xu, X. R-VCANet: A New Deep-Learning-Based Hyperspectral Image Classification Method. IEEE J. Sel. Top. Appl. Earth Obs. Remote. Sens. 2017, 10, 1975–1986. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, H.; Shen, Q. Spectral–Spatial Classification of Hyperspectral Imagery with 3D Convolutional Neural Network. Remote. Sens. 2017, 9, 67. [Google Scholar] [CrossRef] [Green Version]
- Mou, L.; Ghamisi, P.; Zhu, X.X. Unsupervised Spectral–Spatial Feature Learning via Deep Residual Conv–Deconv Network for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote. Sens. 2018, 56, 391–406. [Google Scholar] [CrossRef] [Green Version]
- Zhong, Z.; Li, J.; Luo, Z.; Chapman, M. Spectral–Spatial Residual Network for Hyperspectral Image Classification: A 3-D Deep Learning Framework. IEEE Trans. Geosci. Remote. Sens. 2017, 56, 847–858. [Google Scholar] [CrossRef]
- Zhong, P.; Gong, Z.; Li, S.; Schönlieb, C.-B. Learning to Diversify Deep Belief Networks for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote. Sens. 2017, 55, 3516–3530. [Google Scholar] [CrossRef]
- Liu, Q.; Zhou, F.; Hang, R.; Yuan, X. Bidirectional-Convolutional LSTM Based Spectral-Spatial Feature Learning for Hyperspectral Image Classification. Remote. Sens. 2017, 9, 1330. [Google Scholar] [CrossRef] [Green Version]
- Zhang, C.; Sargent, I.; Pan, X.; Li, H.; Gardiner, A.; Hare, J.; Atkinson, P.M. Joint Deep Learning for land cover and land use classification. Remote. Sens. Environ. 2019, 221, 173–187. [Google Scholar] [CrossRef] [Green Version]
- Li, E.; Xia, J.; Du, P.; Lin, C.; Samat, A. Integrating Multilayer Features of Convolutional Neural Networks for Remote Sensing Scene Classification. IEEE Trans. Geosci. Remote. Sens. 2017, 55, 5653–5665. [Google Scholar] [CrossRef]
- Liu, B.; Yu, X.; Zhang, P.; Tan, X.; Yu, A.; Xue, Z. A semi-supervised convolutional neural network for hyperspectral image classification. Remote. Sens. Lett. 2017, 8, 839–848. [Google Scholar] [CrossRef]
- Yuan, Q.; Yuan, Q.; Li, J.; Shen, H.; Zhang, L. Hyperspectral Image Denoising Employing a Spatial–Spectral Deep Residual Convolutional Neural Network. IEEE Trans. Geosci. Remote. Sens. 2019, 57, 1205–1218. [Google Scholar] [CrossRef] [Green Version]
- Hu, F.; Xia, G.-S.; Hu, J.; Zhang, L. Transferring Deep Convolutional Neural Networks for the Scene Classification of High-Resolution Remote Sensing Imagery. Remote. Sens. 2015, 7, 14680–14707. [Google Scholar] [CrossRef] [Green Version]
- Andrearczyk, V.; Whelan, P.F. Convolutional neural network on three orthogonal planes for dynamic texture classification. Pattern Recognit. 2018, 76, 36–49. [Google Scholar] [CrossRef] [Green Version]
- Anwer, R.M.; Khan, F.S.; Van De Weijer, J.; Molinier, M.; Laaksonen, J. Binary patterns encoded convolutional neural networks for texture recognition and remote sensing scene classification. ISPRS J. Photogramm. Remote. Sens. 2018, 138, 74–85. [Google Scholar] [CrossRef] [Green Version]
- Wang, M.; Zhang, X.; Niu, X.; Wang, F.; Zhang, X. Scene Classification of High-Resolution Remotely Sensed Image Based on ResNet. J. Geovis. Spat. Anal. 2019, 3, 16. [Google Scholar] [CrossRef]
- Breiman, L.; Friedman, J.H.; Olshen, R.A.; Stone, C.J. Classification and regression trees (CART). Biometrics 1984, 40, 874. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Sabale, S.P.; Jadhav, C.R. Hyperspectral Image Classification Methods in Remote Sensing—A Review. In Proceedings of the 2015 International Conference on Computing Communication Control and Automation, Pune, India, 26–27 February 2015; pp. 679–683. [Google Scholar]
- Kussul, N.; Lavreniuk, M.; Skakun, S.; Shelestov, A. Deep Learning Classification of Land Cover and Crop Types Using Remote Sensing Data. IEEE Geosci. Remote. Sens. Lett. 2017, 14, 778–782. [Google Scholar] [CrossRef]
- Dou, P.; Chen, Y.; Yue, H. Remote-sensing imagery classification using multiple classification algorithm-based AdaBoost. Int. J. Remote. Sens. 2017, 39, 619–639. [Google Scholar] [CrossRef]
- Wang, J.; Wu, Z.; Wu, C.; Cao, Z.; Fan, W.; Tarolli, P. Improving impervious surface estimation: An integrated method of classification and regression trees (CART) and linear spectral mixture analysis (LSMA) based on error analysis. GIScience Remote. Sens. 2017, 55, 583–603. [Google Scholar] [CrossRef]
- Noi, P.T.; Kappas, M. Comparison of Random Forest, k-Nearest Neighbor, and Support Vector Machine Classifiers for Land Cover Classification Using Sentinel-2 Imagery. Sensors 2017, 18, 18. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Xi, B.; Li, Y.; Du, Q.; Wang, K. Hyperspectral Classification Based on Texture Feature Enhancement and Deep Belief Networks. Remote. Sens. 2018, 10, 396. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dabboor, D.; Howell, S.; Shokr, E.L.; Yackel, J.J. The Jeffries-Matusita distance for the case of complex Wishart distribution as a separability criterion for fully polarimetric SAR data. Int. J. Remote Sens. 2014, 35, 6859–6873. [Google Scholar]
- Xu, Y.; Du, B.; Zhang, F.; Zhang, L. Hyperspectral image classification via a random patches network. ISPRS J. Photogramm. Remote. Sens. 2018, 142, 344–357. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, L.; Du, B.; Zhang, F. Spectral-Spatial Unified Networks for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote. Sens. 2018, 56, 1–17. [Google Scholar] [CrossRef]
- Tang, Y.Y.; Lu, Y.; Yuan, H. Hyperspectral Image Classification Based on Three-Dimensional Scattering Wavelet Transform. IEEE Trans. Geosci. Remote. Sens. 2014, 53, 2467–2480. [Google Scholar] [CrossRef]
- Kang, X.; Li, S.; Fang, L.; Li, M.; Benediktsson, J.A. Extended Random Walker-Based Classification of Hyperspectral Images. IEEE Trans. Geosci. Remote. Sens. 2014, 53, 144–153. [Google Scholar] [CrossRef]















| Indiana Pines (IP) Dataset | |||
| Class Name | Sample Count | Class Name | Sample Count |
| Alfalfa (AL) | 46 | Oats (OT) | 20 |
| Corn-notill (CN) | 1428 | Soybean-notill (SN) | 972 |
| Corn-mintill (CM) | 830 | Soybean-mintill (SM) | 2455 |
| Corn (CO) | 237 | Soybean-clean (SC) | 593 |
| Grass-pasture (GP) | 483 | Wheat (WH) | 205 |
| Grass-trees (GT) | 730 | Woods (WO) | 1265 |
| Grass-pasture-mowed (GPM) | 28 | Buildings-grass-trees-drives (BGTD) | 386 |
| Hay-windrowed (HW) | 478 | Stone-steel-towers (SST) | 93 |
| Salinas (SA) dataset | |||
| Class name | Sample count | Class name | Sample count |
| Broccoli-green-weeds 1 (BGW1) | 2009 | Soil-vineyard-develop (SVD) | 6203 |
| Broccoli-green-weeds 2 (BGW2) | 3726 | Corn-senesced-green-weeds (CSGW) | 3278 |
| Fallow (FA) | 1976 | Lettuce-romaine-4wk (LR4) | 1068 |
| Fallow-rough-plow (FRP) | 1394 | Lettuce-romaine-5wk (LR5) | 1927 |
| Fallow-smooth (FS) | 2678 | Lettuce-romaine-6wk (LR6) | 916 |
| Stubble (ST) | 3959 | Lettuce-romaine-7wk (LR7) | 1070 |
| Celery (CE) | 3579 | Vineyard-untrained (VU) | 7268 |
| Grapes-untrained (GU) | 11,271 | Vineyard-vertical-trellis (VVT) | 1807 |
| HyRANK-Loukia (HL) dataset | |||
| Class name | Sample count | Class name | Sample count |
| Dense urban fabric (DUF) | 288 | Mixed forest (MF) | 1072 |
| Mineral extraction sites (MES) | 67 | Dense sclerophyllous vegetation (DSV) | 3793 |
| Non irrigated arable land (NIAL) | 542 | Sparse sclerophyllous vegetation (SSV) | 2803 |
| Fruit trees (FT) | 79 | Sparsely vegetated areas (SVA) | 404 |
| Olive groves (OG) | 1401 | Rocks and sand (RS) | 487 |
| Broad-leaved forest (BLF) | 223 | Water (WA) | 1393 |
| Coniferous forest (CF) | 500 | Coastal water (CW) | 451 |
| Pavia University (PU) dataset | |||
| Class name | Sample count | Class name | Sample count |
| Asphalt (AS) | 6631 | Bare Soil (BS) | 5029 |
| Meadows (ME) | 18,649 | Bitumen (BI) | 1330 |
| Gravel (GR) | 2099 | Self-Blocking Bricks (SBB) | 3682 |
| Trees (TR) | 3064 | Shadows (SH) | 947 |
| Painted metal sheets (PMS) | 1345 | ||
| Layers | Filter Size | ReLU | Max-Pooling |
|---|---|---|---|
| Conv-1 | 32 × 5 × 5 | Yes | No |
| MaxPool-1 | 2 × 2 | No | Yes |
| Conv-2 | 64 × 5 × 5 | Yes | No |
| MaxPool-2 | 2 × 2 | No | Yes |
| Conv-3 | 128 × 3 × 3 | Yes | No |
| Output | 2 × 2 | No | Yes |
| Classifier | Description of Parameters |
|---|---|
| CART | The minimum number of samples required to split an internal node: 2. |
| The minimum number of samples required to be at a leaf node: 1. | |
| RF | The number of trees in the forest: 20. |
| The minimum number of samples required to split an internal node: 2. | |
| The minimum number of samples required to be at a leaf node: 1. | |
| DBN | The number of epochs for pre-training: 200. |
| The number of epochs for fine-tuning: 500. | |
| Learning ratio of pre-training and fine-tuning: 0.001. | |
| Batch size: 30. | |
| List of hidden units: [200]. |
| Classifier | Feature Extract Method | Accuracy Evaluations of Different Datasets | Average | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| IP | SA | HL | PU | ||||||||
| OA | Kappa | OA | Kappa | OA | Kappa | OA | Kappa | OA | Kappa | ||
| CART | LSTM | 73.85 | 0.703 | 91.59 | 0.906 | 77.00 | 0.727 | 86.63 | 0.822 | 82.27 | 0.790 |
| MCNN | 85.05 | 0.829 | 95.32 | 0.948 | 66.15 | 0.597 | 85.94 | 0.813 | 83.12 | 0.797 | |
| SSUN | 81.67 | 0.791 | 93.27 | 0.925 | 75.33 | 0.780 | 92.05 | 0.885 | 85.58 | 0.845 | |
| RPNet | 92.17 | 0.911 | 97.28 | 0.970 | 82.32 | 0.790 | 96.98 | 0.960 | 92.19 | 0.908 | |
| 3DSWT | 82.25 | 0.797 | 87.34 | 0.859 | 78.33 | 0.742 | 87.04 | 0.829 | 83.74 | 0.807 | |
| ERW | 92.67 | 0.917 | 99.49 | 0.994 | 93.37 | 0.921 | 96.79 | 0.958 | 95.58 | 0.948 | |
| FRML | 96.30 | 0.960 | 98.19 | 0.980 | 96.30 | 0.960 | 97.98 | 0.973 | 97.19 | 0.968 | |
| RF | LSTM | 85.09 | 0.830 | 94.39 | 0.937 | 85.22 | 0.823 | 90.89 | 0.877 | 88.90 | 0.867 |
| MCNN | 99.08 | 0.990 | 99.19 | 0.991 | 81.56 | 0.776 | 97.12 | 0.962 | 94.24 | 0.930 | |
| SSUN | 95.90 | 0.953 | 96.75 | 0.964 | 85.80 | 0.872 | 96.96 | 0.956 | 93.85 | 0.936 | |
| RPNet | 95.48 | 0.948 | 97.57 | 0.973 | 87.24 | 0.848 | 98.66 | 0.982 | 94.74 | 0.938 | |
| 3DSWT | 95.27 | 0.946 | 98.12 | 0.979 | 94.11 | 0.930 | 95.71 | 0.943 | 95.80 | 0.950 | |
| ERW | 95.60 | 0.950 | 99.67 | 0.996 | 96.37 | 0.957 | 98.96 | 0.986 | 97.65 | 0.972 | |
| FRML | 97.30 | 0.969 | 98.74 | 0.986 | 98.48 | 0.982 | 98.97 | 0.986 | 98.37 | 0.981 | |
| DBN | LSTM | 81.61 | 0.790 | 92.36 | 0.915 | 82.06 | 0.785 | 92.47 | 0.900 | 87.13 | 0.848 |
| MCNN | 76.21 | 0.728 | 95.28 | 0.948 | 61.43 | 0.523 | 88.06 | 0.840 | 80.25 | 0.760 | |
| SSUN | 86.11 | 0.841 | 94.69 | 0.941 | 73.12 | 0.769 | 93.69 | 0.908 | 86.90 | 0.865 | |
| RPNet | 98.07 | 0.978 | 97.67 | 0.974 | 91.94 | 0.904 | 99.23 | 0.990 | 96.73 | 0.962 | |
| 3DSWT | 65.14 | 0.596 | 55.25 | 0.489 | 90.33 | 0.884 | 76.59 | 0.683 | 71.83 | 0.663 | |
| ERW | 99.91 | 0.999 | 99.00 | 0.988 | 97.12 | 0.969 | 99.56 | 0.994 | 98.90 | 0.988 | |
| FRML | 96.29 | 0.958 | 99.02 | 0.988 | 98.15 | 0.978 | 99.67 | 0.995 | 98.28 | 0.980 | |
| Dataset | LSTM | MCNN | SSUN | RPNet | 3DSWT | ERW | FRML | |
|---|---|---|---|---|---|---|---|---|
| SFRM-E | FL-SFRM | |||||||
| IP | 2.768 | 4.463 | 3.126 | 0.436 | 16.761 | 74.936 | 33.722 | 1.173 |
| SA | 10.406 | 15.396 | 17.374 | 2.850 | 83.040 | 367.610 | 63.539 | 3.948 |
| HL | 9.872 | 14.449 | 16.710 | 3.618 | 53.784 | 748.000 | 21.819 | 0.527 |
| PU | 9.859 | 16.780 | 17.496 | 2.813 | 45.207 | 631.628 | 19.182 | 0.712 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dou, P.; Zeng, C. Hyperspectral Image Classification Using Feature Relations Map Learning. Remote Sens. 2020, 12, 2956. https://doi.org/10.3390/rs12182956
Dou P, Zeng C. Hyperspectral Image Classification Using Feature Relations Map Learning. Remote Sensing. 2020; 12(18):2956. https://doi.org/10.3390/rs12182956
Chicago/Turabian StyleDou, Peng, and Chao Zeng. 2020. "Hyperspectral Image Classification Using Feature Relations Map Learning" Remote Sensing 12, no. 18: 2956. https://doi.org/10.3390/rs12182956
APA StyleDou, P., & Zeng, C. (2020). Hyperspectral Image Classification Using Feature Relations Map Learning. Remote Sensing, 12(18), 2956. https://doi.org/10.3390/rs12182956