Climate-Quality Calibration for Low Earth-Orbit Microwave Radiometry †
Abstract
:1. Introduction
2. Radiometer Design
- A phase-locked local oscillator (LO) prevents frequency drift.
- The system response of the amplifiers and detectors should be as nearly as possible linear with input power. An internal noise diode will allow correction of residual non-linearity. Firing the noise diode during part of the viewing time of high and low calibration temperatures yields four calibration points, which can be solved for three coefficients of the instrument transfer function (e.g., a quadratic form) and also the excess noise temperature of the diode [12]. (The noise temperature of the diode is not assumed to be constant.) However, nonlinearity in common amplifier stages can introduce crosstalk between channels because of gain compression [13], which this method will not correct. Therefore, linearity is extremely important for those amplifiers. Digital processing may be useful in this context, given that the non-linearity inherent in binary representation of signals can be corrected analytically [14].
- Instead of total power detection, sensitivity to short-term gain fluctuations within the calibration cycle should be reduced by Dicke-switching, by digital correlation, or by some other means.
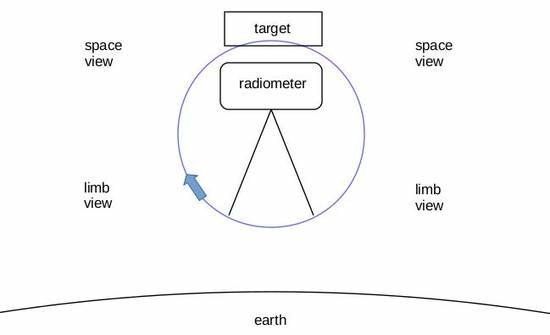
- A low-sidelobe horn antenna without a reflector eliminates spillover of energy at the edge of the reflector, making the directivity pattern accurately calculable. The radiometer section would rotate along with the antenna, to scan the earth and also view cold space and an on-board black-body target, as sketched in Figure 1. A monostatic return loss of 55 dB from 31 to 84 GHz has been measured on a folded inverted-cone target [15]. The antenna should be closely coupled to the target when viewing it.
- The scan should include the earth limbs for comparison of limb radiometric measurements to GNSS radio-occultation (RO) measurements, as discussed below in Section 3. Comparison with radiometric measurements at the limb instead of closer to nadir avoids the difficulties associated with different viewing geometries (e.g., see [16]).
- Dual-polarization measurements, using two radiometers coupled to orthogonal modes of the antenna, allow exact transfer of calibration to rotating-polarization instruments like ATMS, for channels sensitive to surface polarization. For frequencies not sensitive to the surface, the two polarization measurements would be averaged together.
- Control of instrument temperature, including the calibration target, contributes to radiometer stability and also simplifies requirements for pre-launch testing.
3. Co-Located Radio-Occultation Reference
4. Orbit Selection
5. Summary and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| AMSU | Advanced Microwave Sounding Unit |
| ATMS | Advanced Technology Microwave Sounder |
| GNSS | Global Navigation Satellite System |
| LO | local oscillator |
| MSU | Microwave Sounding Unit |
| RO | radio occultation |
| SSMIS | Special Sensor Microwave Imager/Sounder |
| antenna temperature |
References
- Goldberg, M.; Ohring, G.; Butler, J.; Cao, C.; Datla, R.; Doelling, D.; Gärtner, V.; Hewison, T.; Iacovazzi, B.; Kim, D.; et al. The Global Space-Based Inter-Calibration System (GSICS). Bull. Am. Meteorol. Soc. 2011, 92, 467–475. [Google Scholar] [CrossRef]
- Wielicki, B.A.; Young, D.F.; Mlynczak, M.G.; Thome, K.J.; Leroy, S.; Corliss, J.; Anderson, J.G.; Ao, C.O.; Bantges, R.; Best, F.; et al. Achieving climate change absolute accuracy in orbit. Bull. Am. Meteorol. Soc. 2013, 94, 1519–1539. [Google Scholar] [CrossRef] [Green Version]
- Tobin, D.; Holz, R.; Nagle, F.; Revercomb, H. Characterization of the Climate Absolute Radiance and Refractivity Observatory (CLARREO) ability to serve as an infrared satellite intercalibration reference. J. Geophys. Res. Atmos. 2016, 121, 4258–4271. [Google Scholar] [CrossRef] [Green Version]
- Thorne, P.W.; Lanzante, J.R.; Peterson, T.C.; Seidel, D.J.; Shine, K.P. Tropospheric temperature trends: History of an ongoing controversy. Wiley Interdiscip. Rev. Clim. Chang. 2011, 2, 66–88. [Google Scholar] [CrossRef]
- Grody, N.C.; Vinnikov, K.Y.; Goldberg, M.D.; Sullivan, J.T.; Tarpley, J.D. Calibration of multisatellite observations for climatic studies: Microwave Sounding Unit (MSU). J. Geophys. Res. 2004, 109, D24104. [Google Scholar] [CrossRef] [Green Version]
- Bodeker, G.E.; Bojinski, S.; Cimini, D.; Dirksen, R.J.; Haeffelin, M.; Hannigan, J.W.; Hurst, D.F.; Leblanc, T.; Madonna, F.; Maturilli, M.; et al. Reference upper-air observations for climate: From concept to reality. Bull. Am. Meteorol. Soc. 2015, 97, 123–135. [Google Scholar] [CrossRef]
- Kroodsma, R.A.; McKague, D.S.; Ruf, C.S. Vicarious cold calibration for conical scanning microwave imagers. IEEE Trans. Geosci. Remote Sens. 2017, 55, 816–827. [Google Scholar] [CrossRef]
- Yang, H.; Zhou, J.; Weng, F.; Sun, N.; Anderson, K.; Liu, Q.; Kim, E.J. Developing vicarious calibration for microwave sounding instruments by using lunar radiation. IEEE Trans. Geosci. Remote Sens. 2018, 56, 6723–6733. [Google Scholar] [CrossRef]
- Houtz, D.A.; Emery, W.; Gu, D.; Jacob, K.; Murk, A.; Walker, D.K.; Wylde, R.J. Electromagnetic design and performance of a conical microwave blackbody target for radiometer calibration. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4586–4596. [Google Scholar] [CrossRef]
- Rosenkranz, P.W.; Blackwell, W.J.; Gasiewski, A.J.; Leslie, R.V.; Mears, C.A.; Piepmeier, J.R.; Racette, P.E.; Santer, B.D. Designing a Climate-Monitoring Microwave Radiometer. In Proceedings of the USNC-URSI National Radio Science Meeting, Boulder, CO, USA, 4–7 January 2017. [Google Scholar] [CrossRef]
- Blackwell, W.J.; Bishop, R.; Cahoy, K.; Cohen, B.; Crail, C.; Cucurull, L.; Dave, P.; DiLiberto, M.; Erickson, N.; Fish, C.; et al. Radiometer calibration using colocated GPS radio occultation measurements. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6423–6433. [Google Scholar] [CrossRef] [Green Version]
- Draper, D.W.; Newell, D.A.; McKague, D.S.; Piepmeier, J.R. Assessing Calibration Stability Using the Global Precipitation Measurement (GPM) Microwave Imager (GMI) Noise Diodes. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 4239–4247. [Google Scholar] [CrossRef]
- Ochiai, S.; Kikuchi, K.; Nishibori, T.; Manabe, T. Gain nonlinearity calibration of submillimeter radiometer for JEM/SMILES. IEEE J. Sel. Top. Earth Obs. Remote Sens. 2012, 5, 962–969. [Google Scholar] [CrossRef]
- Piepmeier, J.R.; Gasiewski, A.J. Digital correlation microwave polarimetry: Analysis and demonstration. IEEE Trans. Geosci. Remote Sens. 2001, 39, 2392–2410. [Google Scholar] [CrossRef]
- Yagoubov, P.; Murk, A.; Wylde, R.; Bell, G.; Tan, G.H. Calibration loads for ALMA. In Proceedings of the 36th International Conference on Infrared, Millimeter, and Terahertz Waves, Houston, TX, USA, 2–7 October 2011. [Google Scholar] [CrossRef]
- Liu, C.-Y.; Li, J.; Ho, S.-P.; Liu, G.-R.; Lin, T.-H.; Young, C.-C. Retrieval of atmospheric thermodynamic state from synergistic use of radio occultation and hyperspectral infrared radiances observations. IEEE J. Sel. Top. Earth Obs. Remote Sens. 2016, 9, 744–756. [Google Scholar] [CrossRef]
- CoSMIR. Available online: https://atmospheres.gsfc.nasa.gov/meso/index.php?section=121 (accessed on 1 November 2019).
- Kursinski, E.R.; Hajj, G.A.; Leroy, S.S.; Hermann, B. The GPS radio occultation technique. Terr. Atmos. Ocean. Sci. 2000, 11, 53–114. [Google Scholar] [CrossRef] [Green Version]
- Kursinski, E.R.; Hajj, G.A.; Schofield, J.T.; Linfield, R.P.; Hardy, K.R. Observing Earth’s atmosphere with radio occultation measurements using the Global Positioning System. J. Geophys. Res. 1997, 102, 23429–23465. [Google Scholar] [CrossRef]
- Foelsche, U.; Scherllin-Pirscher, B.; Ladstädter, F.; Steiner, A.K.; Kirchengast, G. Refractivity and temperature climate records from multiple radio occultation satellites consistent within 0.05%. Atmos. Meas. Tech. 2011, 4, 2007–2018. [Google Scholar] [CrossRef] [Green Version]
- Cimini, D.; Rosenkranz, P.W.; Tretyakov, M.Y.; Koshelev, M.A.; Romano, F. Uncertainty of atmospheric microwave absorption model: Impact on ground-based radiometer simulations and retrievals. Atmos. Chem. Phys. 2018, 18, 15231–15259. [Google Scholar] [CrossRef] [Green Version]
- Rüeger, J.M. Refractive index formulae for radio waves. In Proceedings of the FIG XXII International Congress, Washington, DC, USA, 19–26 April 2002; Available online: http://www.fig.net/resources/proceedings/fig_proceedings/fig_2002/Js28/JS28_rueger.pdf (accessed on 1 November 2019).
- Leroy, S.; Ao, C.O.; Verkhoglyadova, O.P. Temperature trends and anomalies in modern satellite data: Infrared sounding and GPS radio occultation. J. Geophys. Res. Atmos. 2018, 123, 11431–11444. [Google Scholar] [CrossRef]
- Khaykin, S.M.; Funatsu, B.M.; Hauchecorne, A.; Godin-Beekmann, S.; Claud, C.; Keckhut, P.; Pazmino, A.; Gleisner, H.; Nielsen, J.K.; Syndergaard, S.; et al. Postmillennium changes in stratospheric temperature consistently resolved by GPS radio occultation and AMSU observations. Geophys. Res. Lett. 2017, 44, 7510–7518. [Google Scholar] [CrossRef]
- Leroy, S.; Anderson, J.G.; Ohring, G. Climate signal detection times and constraints on climate benchmark accuracy requirements. J. Clim. 2008, 21, 841–846. [Google Scholar] [CrossRef] [Green Version]
- Mears, C.A.; Wentz, F.J.; Thorne, P.; Bernie, D. Assessing uncertainty in estimates of atmospheric temperature changes from MSU and AMSU using a Monte-Carlo estimation technique. J. Geophys. Res. 2011, 116, D08112. [Google Scholar] [CrossRef]
- Mears, C.A.; Wentz, F.J. Sensitivity of satellite-derived tropospheric temperature trends to the diurnal cycle adjustment. J. Clim. 2016, 29, 3629–3646. [Google Scholar] [CrossRef]
- Mears, C.A.; Wentz, F.J. A satellite-derived lower-tropospheric atmospheric temperature dataset using an optimized adjustment for diurnal effects. J. Clim. 2017, 30, 7695–7718. [Google Scholar] [CrossRef]
- Wentz, F.J.; Schabel, M. Effects of orbital decay on satellite-derived lower-tropospheric temperature trends. Nature 1998, 394, 661–664. [Google Scholar] [CrossRef]


| Parameter | Value | Comments |
|---|---|---|
| (noise-equivalent ) | ≤0.05 K s | for dual-polarization average |
| absolute accuracy of calibration at launch | ±0.1 K | for antenna temperature |
| (long-term calibration stability | K yr | Equation (3), with GNSS-RO reference |
| lifetime frequency stability | ±1 MHz | with phase-locked LO |
| antenna 3 dB beamwidth | 5 | from [11] |
| antenna stray factor (1 – beam-efficiency) | ≤1% | >15 from beam center |
| antenna off-earth stray factor | ≤0.03% | for nadir view |
| non-linearity max. deviation (before correction) | ≤0.1 K | for K |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rosenkranz, P.W.; Blackwell, W.J.; Leslie, R.V. Climate-Quality Calibration for Low Earth-Orbit Microwave Radiometry. Remote Sens. 2020, 12, 241. https://doi.org/10.3390/rs12020241
Rosenkranz PW, Blackwell WJ, Leslie RV. Climate-Quality Calibration for Low Earth-Orbit Microwave Radiometry. Remote Sensing. 2020; 12(2):241. https://doi.org/10.3390/rs12020241
Chicago/Turabian StyleRosenkranz, Philip W., William J. Blackwell, and R. Vincent Leslie. 2020. "Climate-Quality Calibration for Low Earth-Orbit Microwave Radiometry" Remote Sensing 12, no. 2: 241. https://doi.org/10.3390/rs12020241
APA StyleRosenkranz, P. W., Blackwell, W. J., & Leslie, R. V. (2020). Climate-Quality Calibration for Low Earth-Orbit Microwave Radiometry. Remote Sensing, 12(2), 241. https://doi.org/10.3390/rs12020241