Advantages of Uncombined Precise Point Positioning with Fixed Ambiguity Resolution for Slant Total Electron Content (STEC) and Differential Code Bias (DCB) Estimation
Abstract
:1. Introduction
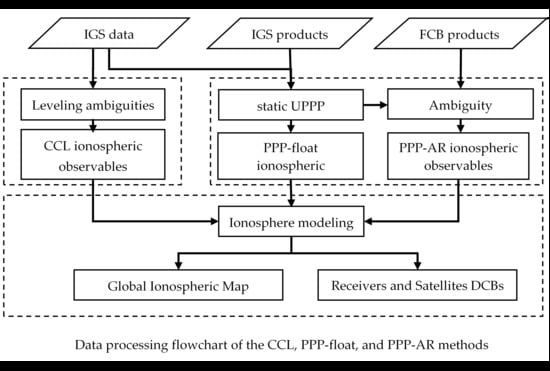
2. Methods
2.1. Basic Code and Phase Observation Equation
2.2. Carrier-to-Code Leveling (CCL) Method
2.3. Uncombined PPP with Ambiguity Resolution
2.4. Ionospheric Modeling and Estimation of DCBs
3. Experiments and Results
3.1. Experimental Setup
3.2. Accuracy of Ionospheric Observables
3.3. Ionospheric Modeling with Three Types of Ionospheric Observables
3.3.1. Self-Generated GIM Products
3.3.2. Accuracy of Ionospheric Observable Residuals
3.3.3. Comparison with CODE GIM Products
3.3.4. Satellites’ DCB Accuracy
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Klobuchar, J.A. Ionospheric Time-Delay Algorithm for Single-Frequency GPS Users. IEEE Trans. Aerosp. Electron. Syst. 1987, AES-23, 325–331. [Google Scholar] [CrossRef]
- Schaer, S. Mapping and Predicting the Earth’s Ionosphere Using the Global Positioning System. Ph.D. Thesis, Dissertation Astronomical Institute, University of Berne, Berne, Switzerland, 25 March 1999. [Google Scholar]
- Rovira-Garcia, A.; Juan, J.M.; Sanz, J.; Gonzalez-Casado, G. A Worldwide Ionospheric Model for Fast Precise Point Positioning. IEEE Trans. Geosci. Remote Sens. 2015, 53, 4596–4604. [Google Scholar] [CrossRef] [Green Version]
- Xu, G.; Xu, Y. GPS: Theory, Algorithms and Applications, 3rd ed.; Springer: Berlin, Germany, 2016; pp. 63–80. [Google Scholar]
- Hernández-Pajares, M.; Juan, J.M.; Sanz, J.; Orus, R.; Garcia-Rigo, A.; Feltens, J.; Komjathy, A.; Schaer, S.C.; Krankowski, A. The IGS VTEC maps: A reliable source of ionospheric information since 1998. J. Geod. 2009, 83, 263–275. [Google Scholar] [CrossRef]
- Brunini, C.; Camilion, E.; Azpilicueta, F. Simulation study of the influence of the ionospheric layer height in the thin layer ionospheric model. J. Geod. 2011, 85, 637–645. [Google Scholar] [CrossRef]
- Xiang, Y.; Gao, Y. An Enhanced Mapping Function with Ionospheric Varying Height. Remote Sens. 2019, 11, 1497. [Google Scholar] [CrossRef] [Green Version]
- Shi, C.; Gu, S.; Lou, Y.; Ge, M. An improved approach to model ionospheric delays for single-frequency Precise Point Positioning. Adv. Space Res. 2012, 49, 1698–1708. [Google Scholar] [CrossRef]
- Banville, S.; Sieradzki, R.; Hoque, M.; Wezka, K.; Hadas, T. On the estimation of higher-order ionospheric effects in precise point positioning. GPS Solut. 2017, 21, 1817–1828. [Google Scholar] [CrossRef]
- Nie, W.; Xu, T.; Rovira-Garcia, A.; Zornoza, J.; Subirana, J.; González-Casado, G.; Chen, W.; Xu, G. The Impacts of the Ionospheric Observable and Mathematical Model on the Global Ionosphere Model. Remote Sens. 2018, 10, 169. [Google Scholar] [CrossRef] [Green Version]
- Nie, W.; Hu, W.; Pan, S.; Wang, S.; Jin, X.; Wang, B. Application of Independently Estimated DCB and Ionospheric TEC in Single-Frequency PPP. In Lecture Notes in Electrical Engineering, Proceedings of the China Satellite Navigation Conference (CSNC) 2014 Proceedings, Nanjing, China, 21–23 May 2014; Sun, J., Jiao, W., Wu, H., Lu, M., Eds.; Springer: Berlin, Germany, 2014; Volume 304, p. 304. [Google Scholar]
- Wang, A.; Chen, J.; Zhang, Y.; Meng, L.; Wang, J. Performance of Selected Ionospheric Models in Multi-Global Navigation Satellite System Single-Frequency Positioning over China. Remote Sens. 2019, 11, 2070. [Google Scholar] [CrossRef] [Green Version]
- Su, K.; Jin, S.; Hoque, M.M. Evaluation of Ionospheric Delay Effects on Multi-GNSS Positioning Performance. Remote Sens. 2019, 11, 171. [Google Scholar] [CrossRef] [Green Version]
- Zhou, F.; Dong, D.; Li, W.; Jiang, X.; Wickert, J.; Schuh, H. GAMP: An open-source software of multi-GNSS precise point positioning using undifferenced and uncombined observations. GPS Solut. 2018, 22, 33. [Google Scholar] [CrossRef]
- Zhou, P.; Wang, J.; Nie, Z.; Gao, Y. Estimation and representation of regional atmospheric corrections for augmenting real-time single-frequency PPP. GPS Solut. 2020, 24, 7. [Google Scholar] [CrossRef]
- Zhang, L.; Yao, Y.; Peng, W.; Shan, L.; He, Y.; Kong, J. Real-Time Global Ionospheric Map and Its Application in Single-Frequency Positioning. Sensors 2019, 19, 1138. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Banville, S.; Collins, P.; Zhang, W.; Langley, R.B. Global and Regional Ionospheric Corrections for Faster PPP Convergence. Navigation 2014, 61, 115–124. [Google Scholar] [CrossRef]
- Tu, R.; Zhang, H.; Ge, M.; Huang, G. A real-time ionospheric model based on GNSS Precise Point Positioning. Adv. Space Res. 2013, 52, 1125–1134. [Google Scholar] [CrossRef]
- Zhang, B.; Teunissen, P.J.G.; Yuan, Y. On the short-term temporal variations of GNSS receiver differential phase biases. J. Geod. 2017, 91, 563–572. [Google Scholar] [CrossRef] [Green Version]
- Brunini, C.; Azpilicueta, F. GPS slant total electron content accuracy using the single layer model under different geomagnetic regions and ionospheric conditions. J. Geod. 2010, 84, 293–304. [Google Scholar] [CrossRef]
- Wang, N.; Yuan, Y.; Li, Z.; Montenbruck, O.; Tan, B. Determination of differential code biases with multi-GNSS observations. J. Geod. 2016, 90, 209–228. [Google Scholar] [CrossRef]
- Xiang, Y.; Gao, Y. Improving DCB Estimation Using Uncombined PPP. Navigation 2017, 64, 463–473. [Google Scholar] [CrossRef]
- Ciraolo, L.; Azpilicueta, F.; Brunini, C.; Meza, A.; Radicella, S.M. Calibration errors on experimental slant total electron content (TEC) determined with GPS. J. Geod. 2007, 81, 111–120. [Google Scholar] [CrossRef]
- Dyrud, L.; Jovancevic, A.; Brown, A.; Wilson, D.; Ganguly, S. Ionospheric measurement with GPS: Receiver techniques and methods: Ionospheric measurement with GPS. Radio Sci. 2008, 43, 1–11. [Google Scholar] [CrossRef]
- Zhang, B.; Teunissen, P.J.G.; Yuan, Y.; Zhang, X.; Li, M. A modified carrier-to-code leveling method for retrieving ionospheric observables and detecting short-term temporal variability of receiver differential code biases. J. Geod. 2018, 93, 19–28. [Google Scholar] [CrossRef] [Green Version]
- Xiang, Y.; Gao, Y.; Shi, J.; Xu, C. Consistency and analysis of ionospheric observables obtained from three precise point positioning models. J. Geod. 2019, 93, 1–10. [Google Scholar] [CrossRef]
- Liu, T.; Zhang, B.; Yuan, Y.; Li, M. Real-Time Precise Point Positioning (RTPPP) with raw observations and its application in real-time regional ionospheric VTEC modeling. J. Geod. 2018, 93, 1267–1283. [Google Scholar] [CrossRef]
- Zhang, B.; Ou, J.; Yuan, Y.; Li, Z. Extraction of line-of-sight ionospheric observables from GPS data using precise point positioning. Sci. China Earth Sci. 2012, 55, 1919–1928. [Google Scholar] [CrossRef]
- Mylnikova, A.A.; Yasyukevich, Y.V.; Kunitsyn, V.E.; Padokhin, A.M. Variability of GPS/GLONASS differential code biases. Results Phys. 2015, 5, 9–10. [Google Scholar] [CrossRef] [Green Version]
- Themens, D.R.; Jayachandran, P.T.; Langley, R.B. The nature of GPS differential receiver bias variability: An examination in the polar cap region. J. Geophys. Res. Space Phys. 2015, 120, 8155–8175. [Google Scholar] [CrossRef]
- Choi, B.-K.; Sohn, D.-H.; Lee, S.J. Correlation between Ionospheric TEC and the DCB Stability of GNSS Receivers from 2014 to 2016. Remote Sens. 2019, 11, 2657. [Google Scholar] [CrossRef] [Green Version]
- Zha, J.; Zhang, B.; Yuan, Y.; Zhang, X.; Li, M. Use of modified carrier-to-code leveling to analyze temperature dependence of multi-GNSS receiver DCB and to retrieve ionospheric TEC. GPS Solut. 2019, 23, 103. [Google Scholar] [CrossRef]
- Li, M.; Yuan, Y.; Wang, N.; Liu, T.; Chen, Y. Estimation and analysis of the short-term variations of multi-GNSS receiver differential code biases using global ionosphere maps. J. Geod. 2018, 92, 889–903. [Google Scholar] [CrossRef]
- Choi, B.-K.; Lee, S.J. The influence of grounding on GPS receiver differential code biases. Adv. Space Res. 2018, 62, 457–463. [Google Scholar] [CrossRef]
- Han, D.; Kim, D.; Song, J.; Kee, C. Improving the Accuracy of Regional Ionospheric Mapping with Double-Difference Carrier Phase Measurement. Remote Sens. 2019, 11, 1849. [Google Scholar] [CrossRef] [Green Version]
- Collins, P.; Lahaye, F.; Heroux, P.; Bisnath, S. Precise Point Positioning with Ambiguity Resolution using the Decoupled Clock Model. In Proceedings of the ION GNSS 2008, Institute of Navigation, Savannah, GA, USA, 16–19 September 2008; pp. 1315–1322. [Google Scholar]
- Ge, M.; Gendt, G.; Rothacher, M.; Shi, C.; Liu, J. Resolution of GPS carrier-phase ambiguities in Precise Point Positioning (PPP) with daily observations. J. Geod. 2008, 82, 389–399. [Google Scholar] [CrossRef]
- Wang, J.; Huang, G.; Yang, Y.; Zhang, Q.; Gao, Y.; Xiao, G. FCB estimation with three different PPP models: Equivalence analysis and experiment tests. GPS Solut. 2019, 23, 93. [Google Scholar] [CrossRef]
- Laurichesse, D.; Mercier, F.; Berthias, J.P.; Bijac, J. Real Time Zero-difference Ambiguities Fixing and Absolute RTK. In Proceedings of the 2008 National Technical Meeting, The Institute of Navigation, San Diego, CA, USA, 28–30 January 2008; pp. 747–755. [Google Scholar]
- Banville, S.; Langley, R.B. Monitoring the ionosphere using integer-leveled GLONASS measurements. In Proceedings of the 28th International Technical Meeting of the Satellite Division of The Institute of Navigation, Tampa, FL, USA, 14–18 September 2015; pp. 3578–3588. [Google Scholar]
- Banville, S.; Zhang, W.; Ghoddousi-Fard, R.; Langley, R.B. Ionospheric Monitoring Using “Integer-Levelled” Observations. In Proceedings of the 25th International Technical Meeting of the Satellite Division of The Institute of Navigation, Nashville, TN, USA, 17–21 September 2012; pp. 2692–2701. [Google Scholar]
- Banville, S.; Langley, R.B. Defining the Basis of an “Integer-Levelling” Procedure for Estimating Slant Total Electron Content. In Proceedings of the 24th International Technical Meeting of the Satellite Division of The Institute of Navigation, Portland, OR, USA, 20–23 September 2011; pp. 2542–2551. [Google Scholar]
- Rovira-Garcia, A.; Juan, J.M.; Sanz, J.; González-Casado, G.; Bertran, E. Fast precise point positioning: A system to provide corrections for single and multi-frequency Navigation. Navigation 2016, 63, 231–247. [Google Scholar] [CrossRef] [Green Version]
- Nie, W.; Xu, T.; Rovira-Garcia, A.; Juan Zornoza, J.M.; Sanz Subirana, J.; González-Casado, G.; Chen, W.; Xu, G. Revisit the calibration errors on experimental slant total electron content (TEC) determined with GPS. GPS Solut. 2018, 22, 85. [Google Scholar] [CrossRef] [Green Version]
- Geng, J.; Meng, X.; Dodson, A.H.; Teferle, F.N. Integer ambiguity resolution in precise point positioning: Method comparison. J. Geod. 2010, 84, 569–581. [Google Scholar] [CrossRef] [Green Version]
- Chen, L.; Yi, W.; Song, W.; Shi, C.; Lou, Y.; Cao, C. Evaluation of three ionospheric delay computation methods for ground-based GNSS receivers. GPS Solut. 2018, 22, 125. [Google Scholar] [CrossRef]
- Xiao, G.; Li, P.; Gao, Y.; Heck, B. A Unified Model for Multi-Frequency PPP Ambiguity Resolution and Test Results with Galileo and BeiDou Triple-Frequency Observations. Remote Sens. 2019, 11, 116. [Google Scholar] [CrossRef] [Green Version]
- Li, P.; Zhang, X.; Ren, X.; Zuo, X.; Pan, Y. Generating GPS satellite fractional cycle bias for ambiguity-fixed precise point positioning. GPS Solut. 2016, 20, 771–782. [Google Scholar] [CrossRef]
- Li, X.; Li, X.; Yuan, Y.; Zhang, K.; Zhang, X.; Wickert, J. Multi-GNSS phase delay estimation and PPP ambiguity resolution: GPS, BDS, GLONASS, Galileo. J. Geod. 2018, 92, 579–608. [Google Scholar] [CrossRef]
- De Oliveira Moraes, A.; Costa, E.; Abdu, M.A.; Rodrigues, F.S.; de Paula, E.R.; Oliveira, K.; Perrella, W.J. The variability of low-latitude ionospheric amplitude and phase scintillation detected by a triple-frequency GPS receiver: Variability of Ionospheric Scintillation. Radio Sci. 2017, 52, 439–460. [Google Scholar] [CrossRef]
- Luo, X.; Lou, Y.; Xiao, Q.; Gu, S.; Chen, B.; Liu, Z. Investigation of ionospheric scintillation effects on BDS precise point positioning at low-latitude regions. GPS Solut. 2018, 22, 63. [Google Scholar] [CrossRef]













| Name | Location | Length(m) | Receiver | Antenna |
|---|---|---|---|---|
| CUT0 | 32.00°S, 115.89°E | 0 | TRIMBLE NETR9 | TRM59800.00 |
| CUT2 | ||||
| EIL3 | 64.68°S, 147.11°W | 0 | ITT 3750300 | TPSCR.G5 |
| EIL4 | ||||
| CUT0 | 32.00°S, 115.89°E | 0 | TRIMBLE NETR9 | TRM59800.00 |
| CUT3 | JAVAD TRE_G3TH_8 | |||
| KOKB | 22.12°N, 159.66°W | 0 | SEPT POLARX5TR | ASH701945G_M |
| KOKV | JAVAD TRE_G3TH | |||
| LCK3 | 26.91°N, 80.95°E | 4.487 | LEICA GRX1200GNSS | LEIAR25.R3 |
| LCK4 | 26.91°N, 80.95°E | |||
| YAR3 | 29.04°S, 115.34°E | 20.210 | SEPT POLARX5 | LEIAR25 |
| YARR | 29.04°S, 115.34°E | LEIAT504 | ||
| GODE | 39.02°N, 76.82°W | 65.160 | SEPT POLARX5TR | AOAD/M_T |
| GODN | 39.02°N, 76.82°W | JAVAD TRE_3 | TPSCR.G3 | |
| WTZ3 | 49.145°N, 12.879°E | 65.669 | JAVAD TRE_G3TH | LEIAR25.R3 |
| WTZA | 49.144°N, 12.879°E | SEPT POLARX2 | ASH700936C_M |
| Items | Strategies |
|---|---|
| Data | 10–16 April 2017 |
| Signal selection | GPS: L1/L2; P1/P2 |
| Observation sampling rate | 30 s |
| Elevation cutoff | 7° for PPP processing; 15° for ionospheric observables |
| Satellite orbit and clock | IGS ephemeris |
| Tropospheric delay | Wet part estimated as random-walk process |
| Ionospheric delay | Estimated as while noise |
| Satellite and receiver antenna | Corrected with the values from IGS |
| Station coordinate | Fixed as constants in IGS SINEX solutions |
| Receiver clock | Estimated as white noise process |
| Phase ambiguities | Estimated as constants, in fixed-ambiguity solution, corrected with FCB products. |
| Others | Relativistic delay, sagnac effect, phase windup effect and tide displacement are corrected with model. |
| GIM | Math Model (degree*order) | Observable | Temporal Resolution | Spatial Resolution | Layers | Stations | System |
|---|---|---|---|---|---|---|---|
| CODE | SH 1 (15*15) | SP4 2 | 1 h | 2.5°*5.0° | 1 | 300 | GPS |
| CCL | SH 1 (15*15) | SP4 2 | 2 h | 2.5°*5.0° | 1 | 268 | GPS |
| PPP-float | SH 1 (15*15) | FL4 (float) 3 | 2 h | 2.5°*5.0° | 1 | 268 | GPS |
| PPP-AR | SH 1 (15*15) | FL4 (AR) 4 | 2 h | 2.5°*5.0° | 1 | 268 | GPS |
| Baseline | STD (ns) | Average (ns) | ||||||
|---|---|---|---|---|---|---|---|---|
| CCL | PPP-Float | Improvement | PPP-AR | Improvement | CCL | PPP-Float | PPP-AR | |
| CUT0-CUT2 | 0.12 | 0.05 | 58.2% | 0.03 | 72.6% | 0.23 | 0.27 | 0.26 |
| CUT0-CUT3 | 0.54 | 0.13 | 76.7% | 0.05 | 91.1% | −18.96 | −17.77 | −17.77 |
| EIL3-EIL4 | 0.08 | 0.03 | 68.3% | 0.01 | 84.3% | −1.23 | −1.25 | −1.25 |
| YAR3-YAR4 | 0.19 | 0.10 | 45.6% | 0.09 | 53.6% | −1.07 | −1.15 | −1.14 |
| WT3-WTZA | 0.30 | 0.08 | 74.2% | 0.04 | 86.3% | 16.86 | 16.16 | 16.16 |
| KOKB-KOKV | 0.33 | 0.11 | 65.8% | 0.09 | 72.4% | −5.93 | −4.62 | −4.63 |
| LCK3-LCK4 | 0.13 | 0.04 | 69.4% | 0.02 | 83.4% | 0.82 | 0.84 | 0.83 |
| GODE-GODN | 0.43 | 0.35 | 19.7% | 0.28 | 36.3% | −1.32 | −0.86 | −0.89 |
| Model | CCL | PPP-Float | PPP-AR |
|---|---|---|---|
| Averaged RMS (TECU) | 0.910 | 0.685 | 0.656 |
| Model | CCL | PPP-Float | PPP-AR |
|---|---|---|---|
| Averaged RMS (TECU) | 1.184 | 1.075 | 1.022 |
| Model | CCL | PPP-Float | PPP-AR |
|---|---|---|---|
| Averaged RMS (ns) | 0.037 | 0.035 | 0.026 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Huang, G.; Zhou, P.; Yang, Y.; Zhang, Q.; Gao, Y. Advantages of Uncombined Precise Point Positioning with Fixed Ambiguity Resolution for Slant Total Electron Content (STEC) and Differential Code Bias (DCB) Estimation. Remote Sens. 2020, 12, 304. https://doi.org/10.3390/rs12020304
Wang J, Huang G, Zhou P, Yang Y, Zhang Q, Gao Y. Advantages of Uncombined Precise Point Positioning with Fixed Ambiguity Resolution for Slant Total Electron Content (STEC) and Differential Code Bias (DCB) Estimation. Remote Sensing. 2020; 12(2):304. https://doi.org/10.3390/rs12020304
Chicago/Turabian StyleWang, Jin, Guanwen Huang, Peiyuan Zhou, Yuanxi Yang, Qin Zhang, and Yang Gao. 2020. "Advantages of Uncombined Precise Point Positioning with Fixed Ambiguity Resolution for Slant Total Electron Content (STEC) and Differential Code Bias (DCB) Estimation" Remote Sensing 12, no. 2: 304. https://doi.org/10.3390/rs12020304
APA StyleWang, J., Huang, G., Zhou, P., Yang, Y., Zhang, Q., & Gao, Y. (2020). Advantages of Uncombined Precise Point Positioning with Fixed Ambiguity Resolution for Slant Total Electron Content (STEC) and Differential Code Bias (DCB) Estimation. Remote Sensing, 12(2), 304. https://doi.org/10.3390/rs12020304