1. Introduction
Human exploration of space encounters several challenges for enabling settlements on the Moon and solar planets. This, in particular, concerns the increased applicability of lunar resources for supporting human survival and energy supply. It is important to efficiently identify, characterize, extract, and process lunar resources, along with the lessons learned from the Apollo missions [
1]. A relevant issue is the economic feasibility of energy production and the use of
3He resources as fuel, potentially even exporting it back to the Earth. For instance, it is expected that the amount of
3He on the Moon is at least 6.5 × 10
8 kg, which shows promising signs for operational purposes if mined efficiently [
2].
On the Earth’s surface,
3He is mainly found as primordial nuclides escaping from the crust to the atmosphere and outer space [
3]: it has also been produced in small quantities in the past [
4]. The strong motivation for the commercial use of
3He comes from its potential to produce clean energy in nuclear fusion reactors. Earthly supplies are currently insufficient for large-scale production, whereas the Jovian planets offer a great opportunity to explore the extractability of highly abundant
3He, however, with some limitations including longer expedition periods, stronger gravitational influence, and lack of solid surface [
2].
Spatially varying weathering governs the implantation of
3He into the lunar soil. A major product includes glass welded aggregates composed of surrounding glass and mineral fragments formed during the melting of soil [
5]. Such regoliths appear darker in reflectance spectroscopy because of the deposition of larger iron particles within recycled grains and enrichment of nanophase metallic iron (npFe
0) in accreted rims [
4,
6]. Weathering also affects the spectral properties: the continuum slope reddens with an increase in the exposure of lunar regoliths, whereas both reflectance and spectral contrast decrease in terms of mafic absorption band depth [
7].
One of the weathering agents is solar wind, a stream of charged particles from the Sun. When interacting with the Moon, it results in: (a) an uninterrupted passage of magnetic field components through the Moon and (b) implantation of hot ionized particles. To date,
3He concentrations (of about 20 ppb) in some lunar soils are precisely known [
8,
9,
10]. The abundance of stable
3He depends on both the solar wind supply and the retention of implanted
3He, whereas the less stable inter-grained
3He is additionally controlled by the surface temperature [
11]. Retention is further governed by the maturity of the regolith and abundance of electro-conductive minerals like ilmenite [
10,
12]. Thus, more
3He is retained in mature regoliths with higher ilmenite abundances.
Several research activities have been carried out in retrieving
3He abundance by incorporating the solar wind fluence and optical properties of the regolith in conjunction with the Clementine UVVIS and Apollo landing site data [
8,
9,
10,
11]. The Clementine UVVIS data have limited capabilities because of their low spectral resolution and difficulties in calibration, thereby leading to ineffective retrieval of surface maturation and
3He predictions. The physical properties of lunar grains are also controlled by the impact of solar wind plasma. This includes a dielectric variation of the soil which affects the degree of attenuation of electromagnetic radiation when interacting with the regolith, and provides additional insights into the physical characteristics of the regolith for implanting solar wind
3He. Furthermore, differences in the scattering mechanism of regoliths are characterized by different geomorphologic features and their orientations with respect to the surface.
Physical properties of the lunar surface have been mapped with radar astronomy [
13]. The bistatic radar imaging of the Moon by the Lunar Reconnaissance Orbiter (LRO) and Earth-based Arecibo Observatory has provided new perspectives of the regolith’s behavior in the presence of volatiles, mainly through a coherent backscattering opposition effect that has not been observed during monostatic campaigns: the circular polarization ratio (CPR) increases at smaller bistatic angles [
14,
15]. The physical nature of the regolith in terms of dielectric characterization at both global and local scales, however, has not been explored yet. Furthermore, lunar topography is poorly associated with the overall repository of
3He. Hence, there is little knowledge of the spread of
3He concerning depth. This depth component may provide information on potential abundant sources of
3He.
The present work contributes to a better understanding of the retention of solar wind implanted 3He into the lunar regolith. It determines the spatial orientation of future 3He mining reserves while considering the depth decay profile of incoming 3He. This includes developing a quantitative 3He retention model by evaluating the optical effects of space weathering on regolith materials. Moreover, the study aimed to extract the physical properties of the regolith using a novel inversion method that utilizes the potential of machine learning (ML) on solving complex dielectric inversion problems. Here, we employed a physical forward model to provide a large number of realistic learning examples for the ML method. Ultimately, it aims to perform the integration of multi-wavelength datasets for understanding the influence of surface processes on 3He retention.
2. Study Area
The study area was the Vallis Schroteri region, being the largest sinuous lunar rille (
Figure 1). The rille emerges in the vicinity of the craters Aristarchus and Herodotus, while its morphologic features spread across the plateau on the nearside of the Moon [
16,
17]. The plateau is known for its geological diversity in exhibiting regolith depositions of volcanic and impact-related origin [
18,
19]. Crustal-anorthositic materials mantled by iron-rich pyroclasts and basaltic lava flows display a complex stratigraphic relationship between different features in the plateau [
20,
21]. Due to the lava emplacement of the crustal layers intermixed with fresh ejecta and dark glassy enrichment, the plateau resembles a topographically elevated terrain of about 2 km relative to that of the surrounding mare regions [
21].
Emplacement scenarios of lava similar to that of the terrestrial volcanic construct of the Mauna Loa eruption have been observed. The region of the plateau is characterized by thick pyroclastic deposits of about 20 m, commonly referred to as dark mantled deposits (DMDs) [
13,
18]. It is a low albedo stratigraphic unit of glassy spheroids with possible emplacement in the Imbrian period (3.7 Ga–3.6 Ga) through large localized lava fountaining events [
18,
22]. This is aligned with the formation processes of the Vallis Schroteri rille. Previous studies have shown the potential of DMDs to preserve up to 300 ppm of indigenous water [
18,
19,
20,
21]. The diversity of the Aristarchus plateau, with a special emphasis on the association of the possible bimodal volcanism of the Cobra head and presence of pyroclastic deposits, makes it a significant nearside candidate for estimating the
3He content, thereby potentially testing in situ resource utilization (ISRU) technologies.
4. Results and Analysis
4.1. Quantitative Estimation of Retained 3He from Chandryaan-1 M3Spectroscopy
Sites near the Cobra Head feature and Herodotus crater received an increased fluence of about 40% relative to other geomorphological features [
37]. Several highly sloped terrains exhibited reduced plasma flux contents adjacent to the areas with relatively larger accumulation. Moreover, the floor of the bowl-shaped microcraters near the vicinity of the Vallis Schroteri depicted almost negligible fluxes compared to the walls. Furthermore, the estimated solar wind flux across the plateau appeared to be normally distributed, where the associated uncertainty was represented by a standard deviation of 0.03 with the most probable relative flux value of 0.29.
From the analysis of our retention model, we observed a significant correlation between the hybrid parameter and laboratory-measured
3He (
Figure 3b). The spatial extent of returned samples from a landing site is necessarily small, and the
3He variations could be assumed to be minimal. Hence, the irregular distribution of the samples in the plot may be attributed to measurement bias. To minimize the bias, averaging of the samples was performed for each site, resulting in a higher correlation coefficient of 0.93. From
Figure 3a, we also observed that the most abundant regions were pyroclastic deposits with
3He concentration >7.3 ppb. Moreover, the floor of the Herodotus crater showed significant diversity in the
3He distribution. The central part showed a medium to high concentration while the spatial extent mantled by ejecta cover showed a lower
3He content.
Several hotspots of higher modeled abundance were marked and were associated with reduced mafic absorption band depths compared to the unweathered regolith grains. Additionally, the sites over the top of the Agricola Mountains exhibited higher redness in the continuum slope. The ejecta cover represented the lowest
3He concentration (≈1.45 ppb), mainly because of the highland materials in the immature grains mixed with impact glasses and sufficiently low ilmenite content. By extracting and analyzing the samples, we estimated that 68% of the weathering contributed to the gradual darkening of the ejecta regolith. Furthermore, the lower modeled abundance of retained
3He, particularly near the inner rille, was attributed to high albedo and immature regolith. Referring to
Table 3, the correlation significantly improves after averaging of site-dependent samples and hence, resolves the bias (as observed in
Figure 3b) to some extent. Comparing the predicted
3He values at the Apollo and Luna landing sites with the actual values yielded a standard error of 1.19 ppb by weight. More details on the comparison are presented in
Appendix A.
Figure 4 shows that variation in the maturity of the regolith contributed to the retention dynamics of implanted
3He, with the maximum continuum slope occurring in the pyroclastic regions. Additionally, we observed higher band depth ratios at the regional level compared to albedo. Quantitatively, the pyroclastic regoliths captured most of this effect with 48% contributing to the attenuation of mafic absorption band depths. In some sub-regions, there were prominent deposits, denoted in green tints mixed with yellow color, potentially exhibiting signatures of nanophase iron particles produced during the vaporization of iron-bearing mafic minerals. This was confirmed by the proportion of continuum slope in the regional pyroclastic soils, which was about 40%, thereby commenting on their high maturity nature. Moreover, the walls of the Herodotus crater and Vallis Schroteri had low slope values. Several other features over the Agricola Mountains and those lying near to the rilles represented a decrease in the continuum slope parameter. The floor of the Herodotus crater was characterized by a medium to high level integrated band depth ratio, accounting for 38% in the spectral alteration process of the regolith. The least dominant factor was the continuum slope, accounting for 25%.
The spectra showed an absorption dip at 1000 nm associated with minor absorption features at 2800 nm, indicating olivine deposits subject to hydration. The ejecta regolith was devoid of mafic minerals; ejecta regolith areas close to the Herodotus crater, however, contained hydrated olivine inclusions (E3 and E8 in
Figure 4). The immature regions, represented as albedo features in a dark tone, were marked with reduced amounts of
3He. In
Figure 4, magenta denotes a high albedo and a continuum slope relative to the integrated band depth ratio, green an equal proportion of continuum slope and integrated band depth ratios, while yellow indicates the pyroclastic regolith that captures higher attenuation of band depths relative to albedo and reddening, with several sub-regions exhibiting green tints over it. We observed non-uniform maturity trends in lunar materials, concerning local weathering effects, thereby influencing the retention.
4.2. Spatial Variations of 3He with Respect to Depth
Modeling the exponential decay profile shows that the abundance of
3He in non-pyroclastic regoliths exhibits contradictory behavior with the concentrations in
Figure 3a. The relative spatial distribution after accommodating the regolith thickness profile suggests an overall decrease of about 25% compared to the rest of the region excluding the ejecta cover. Moreover, the increased
3He content per unit area at a few locations indicates the diverse geochemical constraints of the soil.
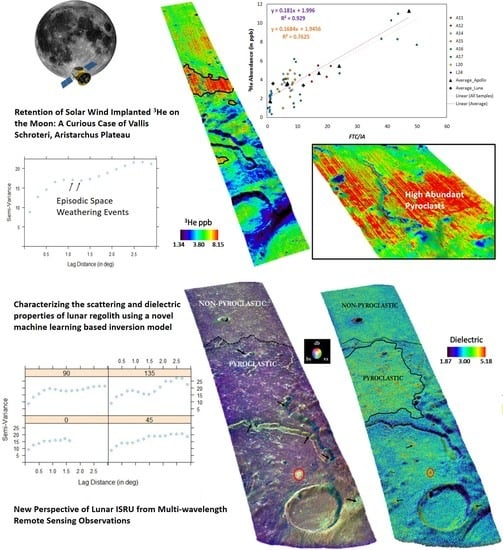
Figure 5a shows the empirical variogram of 8000 randomly sampled points from the low, medium, and high
3He abundant zones. The observed nugget effect was consistent in all directions (
Figure 5b), whereas the sill was not reached in the variogram trend, suggesting a longer correlation length.
Considering the intermediate-scale variance, we observed a cyclic pattern in the semi-variance estimates. Weathering of the lunar soil and maturity of the regolith tended to be repetitive in their occurrences. The black arrow indicates an irregular temporal cycle of geologic events. At this interval, the semi-variance was low, indicating a higher correlation of the modeled abundance, the so-called “hole” effect. This is most likely due to the intrinsic micro-scale changes, along with non-retentive characteristics of the soil.
The overall spatial variability of the modeled abundance showed some anisotropy, where the 135° direction exhibited the clearest hole effect, and the variability in the 0° direction followed an exponential trend, thereby exhibiting higher spatial autocorrelation within lag distances of 0.5 deg. The observed pattern replicates the deterministic implantation process where the spatial correlation disappeared after 0.75 deg. As the lunar regolith erodes once every 20 million years, the intensity and frequency of the cyclic pattern are rather weak. We further noticed a systematic increase in the modeled 3He abundance from proximal to distal regions, oriented at 45°, of the Vallis Schroteri. This decreases the spatial correlation as the lag distance increases. The variogram in the 90° direction showed that the variogram reached its sill at around 1 deg, with a slightly undulating shape.
Figure 6a shows that the green color patches in the top portion of the image were the result of ilmenite dichotomy, where the effects of weathering were largely reduced. The quantitative abundance of the sub-region parallel to the linear rille resembled the proportions derived from
Figure 3a. The mean areal concentration of
3He equaled 16.40 ppb m
−2, as in
Figure 6b.
4.3. Physical Properties of Lunar Regolith Using Bistatic Mini-RF S-Band Data
Figure 7a shows that the typical regolith material predominately behaved as a Bragg surface to the incident radar wave, thereby producing specular or surface scattering mechanisms because of the smooth texture of the regolith devoid of cm- to m-scale scatterers. The presence of larger aggregates in the soil eventually introduced an even bounce scattering response. Moreover, steep slopes over the Agricola Mountains signified the double bounce geometry concerning a relatively smooth regolith. There were several occasions of mixed scattering behavior, like the ejecta cover, a terraced wall of the Vallis Schroteri, and freshly formed microcraters. The ejecta blanket was characterized by volume and double bounce scattering. The anomalously high CPR values in the ejecta materials, along with enhanced volume scattering power, further confirmed the hydration behavior, as indicated in the spectral data analysis.
In
Figure 7b, pyroclastic regoliths were characterized by a mean CPR of 0.31, with higher values attributed to the presence of microcraters. This is in close agreement with [
38]. Additionally, a dominant surface scattering mechanism was observed mainly because of its fine-grained structure and absence of large-sized heterogeneities. The scattering patterns showed that the micro-crater had a mixed dihedral and volume scattering response due to its freshly excavated material. However, the CPR indicator showed a much lower estimate of approximately 0.21, possibly suggesting small-scale roughness.
From the IEM simulations, we observed a decreasing trend of the polarized radar echo with the increase in incidence angle in
Figure 8. This was denoted by enhanced scattering powers from the top regolith for
θ < 25°. However, the regolith with rock inclusions predominated the scattering behavior for larger incidence angles. Additionally, attenuation of the radar echo became stronger in the subsurface due to the larger radar signal path length at a higher incidence. Hence, it is expected that the dominant scattering mechanism in the S-band frequency is essentially coming from the surface and desiccated rocks mixed with the regolith. This was confirmed in
Figure 7a, which indicates the dominance of the blue color (Bragg scattering) over the yellowish-green color (mixed scattering response) in the regolith. With increasing dielectric constant, the Fresnel reflection coefficients increased the surface scattering contribution. Similarly, the radar backscatter was also influenced by surface roughness, which can be compared to the incident wavelength: the backscattering coefficient increased with an increase in the RMS height. This was attributed to the possible orientation of the regolith materials, exhibiting higher Fresnel reflectivity in the HH polarization.
The trend was more evident beyond 1.65 cm RMS height and increased significantly for larger height. In
Figure 8, the red color intensity decreased uniformly for HH polarization compared to the radial trend for VV polarization. There was an average −3.25 dB difference between the sensitivity of the horizontal backscatter and vertical backscatter to the dielectric constant. A possible explanation is that minor changes occur in the penetration depths of different polarizations.
In the MLP neural network, the training of 15,600 patterns requires approximately 23.35 s of central processing unit (CPU) time on high-performance computing (HPC) with 3.4 GHz Xeon E7 with 40 cores. The achieved training R2 value equals 0.985 at approximately 175 iterations. Testing the trained network on 3120 radar backscatter patterns yielded an R2 value equal to 0.987. Nearly equal training and testing R2 values signified that the model was not overfitted. Furthermore, validation showed an accuracy equal to RMSE = 0.26 and MAE = 0.13, respectively. Moreover, the estimated degree of the model prediction error equaled 0.996, indicating a strong agreement with the observed dielectric constants.
From the Apollo landing sites, monostatic datasets were fed into the network as bistatic scenes were absent. A comparison of the predicted and measured values showed a low inversion error for all the reported sites (
Table 4). However, the reliability of the inversion was restricted by the sample space, which proved to be a limitation in this case.
Figure 9 predicts the modal dielectric constant of the regolith as 2.92 with a standard deviation of 0.17. The extensive mantling of fine-grained deposits in the pyroclastic regolith exhibited a high value of dielectric constant. The boundary between the mare deposits and pyroclastic units, denoted by the dotted black line, was similar to the m-Chi decomposed image in
Figure 7a. The blue color in the image characterizes the agglutinated regolith with a low dielectric constant, suggesting an exposed soil–rock interface to the incident radar wave. Several microcraters present in the nearby vicinity of the Vallis Schroteri, marked by black arrows, displayed a predominantly yellow to red color due to the relatively younger regolith.
The floor of the Vallis Schroteri was characterized by high dielectric permittivity, possibly reflecting the volcanic nature of the deposits. It may be expected that the floor contains larger pyroclastic enrichment compared to the marked area (solid black line). This is due to the closer proximity of the regolith to the source volcanic vent, Cobra head. Despite the categorization of dielectric contrast, the values showed relatively low to moderate variations in the region on a global perspective, thereby revealing the physical character of the regolith.
4.4. Understanding the Impact of Surface Processes on the 3He Retentions from Multi-Sensor Perspectives
Figure 10 shows that the relatively younger regolith of the ejecta contains excavated feldspathic highland material associated with low dielectric constant. The retention of
3He tends to decrease for the regolith characterized by reduced dielectric constant values, as shown in
Figure 10b. Moreover, it is influenced dramatically by volume scattering as compared to the double bounce scattering mechanism as in
Figure 10c. The correlation coefficient declined from 0.5 to 0.34. Since the increased volume scattering originates from the buried anisotropic particles, this is particularly interesting for exploration perspectives. There was a surge in the modeled
3He abundance with the CPR.
Figure 10a shows a correlation coefficient equal to 0.55. However, the CPR was low for the entire region, yielding an average pixel value of 0.27, indicating that the variations were caused by roughness.
The cross-variogram analysis in
Figure 11 showed a slightly cyclic pattern at higher lag distances. The modeled abundance was correlated with the surface scattering mechanism at lower lag distances, as observed from
Figure 11b. The cross-variogram also flattened off at higher lag distances, which may be linked to the negative correlation of the
3He concentration with surface scattering patterns in the ejecta regolith.
Figure 11a shows a pure nugget effect. Moreover, there was a spatial autocorrelation between the modeled
3He abundance and surface scattering power in pyroclastic regoliths. This can be observed in
Figure 7a with a dominant blue color.
The unboundedness of the spatial pattern emphasizes the relation between both variables. There was a slight dip in the trend before the increment. The reason may be the presence of microcraters responsible for increased roughness variations and lower surface scattering powers. Meanwhile, the associated modeled abundances, being higher than normal, suggest a negative correlation with surface scattering. In contrast, the cross-variogram for the CPR was opposite to the previous case because the representation involves multiple scattering events like dihedral and volume, arising from the immature microcraters.
5. Discussion
5.1. Retention of Solar Wind Implanted 3He on the Moon
Mechanical influences, like the directional slope component and varying regional topography, play a key role in reducing the uncertainties in modeling plasma fluence at the local scale. The percent change of the modeled flux reading was somewhat surprising: a region tended to receive more than 47% of the plasma flux when the local incidence was not considered compared to topographically normalized modeled flux. This trend was a clear overestimation of the relative flux, thereby associating inaccurate modeled 3He abundance. The observed standard deviation of the distribution equaled 5.47%, therefore, we assumed the presence of prospective 3He sites near the Cobra Head feature based on the higher exposure of solar wind plasma. The decrease in the reddening of the spectra of features in the vicinity of primary rille was mainly caused by the deposition of the immature material on the surface, either through mass wasting or to local impact events. Hence, both local maturity and pyroclastic content govern the estimation of the continuum slope. For instance, on the floor of the Herodotus crater, the weathered regolith is representative of the higher attenuation of mafic absorption band depths than darkening and reddening effects. Additionally, the ejecta cover overlaying the Herodotus crater exhibited high albedo, which represents the freshly excavated material from several depths.
Several factors contribute to the retention of
3He, particularly in the pyroclastic deposits. Concerning the spectral properties, the presence of glass-rich materials indeed enhances the
3He concentration. We already observed that the attenuation of spectra from pyroclastic deposits was higher compared to the spectra from the ejecta cover. Based on these two regions, we can derive the limit of modeled
3He abundance. First, we found that the contribution of albedo was lowest, mainly due to the immature regolith, resulting in larger granular size, which provides less surface area to volumetric weight for the incoming
3He from the solar wind. Second, as the spectra from the pyroclastic region attenuated most, we further explored the retention dynamics of
3He. Interestingly, the results showed that there was a high dependence of the integrated band depth ratio parameter for the modeled
3He abundance. This demarks the pyroclastic deposits as a highly abundant zone. Moreover, the greenish tone overlaid on the yellow surrounding of the pyroclastic regolith in
Figure 4 showed the dominance of the reddening and band depth attenuation effects compared to the albedo, which contributed to the high prediction of
3He.
The reasons behind the findings are the presence of glass-rich materials and the granular structure of the regolith. The latter effect enhanced the modeled abundance as achieved from the spectral effects of the former. Even from the analysis of Apollo data (in
Table 5), particularly for the dark mantle deposit sample 76501 from the Apollo 17 landing site, we saw a higher
3He concentration of 8.8 ppb for grain sizes less than 20
m compared to that of the higher granular size where the concentration reduced to around 1.0 ppb. Upon comparison with a light mantle deposit (sample 72501) and an orange (sample 74220), the abundance dropped to 5.8 ppb and 1.1 ppb, respectively, for the grain size of less than 20
m. This difference clearly showed a varying glass content in the regolith sample materials, which in turn made the spectral properties an important indicator. Although the orange soil sample was Ti-rich, the presence of glass-rich material dominated the retention mechanism.
An interesting trend was observed in the spatial distribution of 3He: soils with sufficiently larger band depth ratios and continuum slopes retained most of the implanted 3He. This was evident in the outer vicinity of the Cobra Head feature with about 58% of albedo, where the presence of irregular-shaped mineral fragments reduced the retention capabilities of the soil. In such cases, the size of the welded aggregates tended to be larger and it took time to break grains down into smaller sizes, thereby reducing the surface area for the incoming solar wind 3He. Despite a relatively higher ilmenite content, the albedo trends suppressed the regolith and made it less retentive. As the reddening spectral effect is controlled by pyroclastic content, the regoliths with significant continuum slope values retained higher 3He content. In terms of economic feasibility and mining excavator capabilities, the fine-grained, volatile-rich pyroclasts emerge out to be suitable regolith for ISRU operations. The additional presence of hydroxyl ions encapsulated within the granular structure of the soil provides immediate attention for exploring the site.
5.2. Spatial Orientation of Retained 3He
Spatial variability of 3He showed instances of large variation for adjacent sampling cells. The uncertainty in the 3He measurement corresponding to an assigned spatial extent induced a higher nugget effect. Moreover, the spatial patterns observed in the vertical direction provided evidence of small-scale periodic processes influencing the retention scenario of 3He. One such minor effect may be the sequential trap and release of weakly bound inter-grained 3He due to its unstable behavior toward temperature variation. Additionally, the sputtered 3He particles from the less retentive soil tended to latch with the defects in the crystal lattice.
The vertical variogram captured the additional semi-variance from the stratigraphic layering of the lunar surface. The small-scale petrological variations were often difficult to interpret compared to apparent large-scale stratigraphic differences. This became prominent in the directional variograms. For the areal repository of 3He, we saw that the ilmenite content was stronger than other local weathering in the retention process. The distinctness in the modeled 3He abundance was apparent for some concentrated sub-regions, where an equal contribution occurred of reddening and attenuated band depth effects. Furthermore, the average regolith thickness of the region was comparatively low, suggesting lower retention with Ti deficient soils.
Since the vertical distribution of 3He tended to reduce at greater depths, the thicker regolith of the Agricola Mountains weakly influenced the modeled abundance. Thus, mining strategies could be planned for extracting potential 3He volatiles from regoliths with higher ilmenite percentage and optimal thickness with respect to the bedrock. Additionally, the contribution of reddening and attenuated mafic band depth on the retention was significant in delineating the 3He-rich soils.
5.3. Physical Properties of Lunar Regolith
The analysis of Mini-RF data showed the potential of ejecta cover to hold on the buried impact melt glasses, which comes in the category of the cm- to m-scatterer. This indicates that there may be some fresh deposits located at around the 1 m depth within the penetration capabilities of the incident radar wave. These inclusions may contribute to the additional subsurface scattering mechanisms, thereby explaining the significance of mixed ejecta behavior. Furthermore, pyroclastic deposits offer an exploratory perspective of distinct radar response compared to the basaltic mare regolith. The lack of cm- to m-scatterers in the regolith contributed to the dominant surface scattering, while the large-sized buried rocks in the non-pyroclastic region provided the hazy appearance with the included diffuse scattering component.
The inversion model showed that lower dielectric constant values may implicate a higher rate of regolith mixing derived from the prolonged cratering process, thereby resulting in an increased vertical roughness. The penetration of the radar echo thus decreased with a higher proportion of rocks brought to the near-surface from deeper regoliths. The higher dielectric constant of the floor of Vallis Schroteri may be due to the closer proximity of the regolith to the source volcanic vent at Cobra Head. The remarkably higher backscatter arising from the steeply sloped bedrock material with minimal deposition of soil exhibited an increased dielectric contrast relative to the surrounding regolith. Despite the categorization of dielectric contrast, the values showed relatively low to moderate variations in the region at a global perspective.
5.4. Influence of Physical Properties on the Retention of Implanted 3He
Since the incoming solar wind represents a hot ionizing radiation wave, the high dielectric contrast of the regolith may lead to increased sputtering events. This was mainly influenced by the high compaction rate of the regolith. Moreover, penetration of the solar wind plasma in the loosely packed regolith may cause implantations at slightly greater depths. In the ejecta cover, the materials were eventually marked with increased hydration from the spectroscopic analysis. Such an increase may be associated with volume scattering, wherein the specific hotspots of high dielectric constant are formed. Retention of 3He is thus mainly related to the dipole-like grains buried within the gardened regolith. Moreover, in some of the instances, these grains contained exposures of hydroxyl ions, which prove significant for large-scale extractions.
The cyclic pattern in the cross-variogram supports the influence of the reddening effect in addition to the albedo patterns on the retention mechanism across the ejecta cover over the geological timescale. Additionally, it could be inferred that the occurrence of the former effect is comparatively after the latter. One of the space weathering processes that dominate the spatial extent of ejecta materials is the albedo, possibly due to the freshly excavated materials from impacts. This yields a higher content of nanophase iron particles reduced from Fe2+, which decreases the retention with time. Gardening of the regolith is sufficiently high in the ejecta cover due to several microimpacts, which can be seen from increased reddening of several microcraters. In the pyroclastic regolith, increased 3He content was associated with a medium to high range of the dielectric constant. This may be due to the domination of attenuated absorption band depths on relatively matured fine-grained pyroclasts mantling the regolith. Such relation links the physical character of the regolith to 3He accumulation on the Moon.
6. Conclusions
We can conclude that the most promising mining candidates are the pyroclastic deposits, regolith over the Agricola Mountains, the unmantled floor of the Herodotus crater, and several hotspots in the nearby vicinity of the Vallis Schroteri. Reddening of the soil and attenuated mafic absorption band depths dominated the weathering factors for delineating the high 3He abundant zones. The distribution was greatly influenced by the electro-conductive nature of ilmenite as an important retention proxy. The variogram of 3He exhibited cyclicity associated with the periodicity over the geological timescale, as can be explained by weathering processes.
The physical properties of the regolith showed that pyroclastic deposits have an increased response of surface scattering and a moderate to high dielectric constant, possibly due to the fine-grained structure and enhanced hydration. The study further noted that lower abundant regolith of the ejecta cover represented a relatively high correlation with volume scattering. This was attributed to the presence of dipole-like features buried within the regolith. Cyclicity of the cross-variograms at a higher lag distance indicated a reddening contribution to an already albedo-dominated nature within the gardened ejecta regolith. In this regard, our study demonstrates the prospectivity of a lunar site from a 3He resource viewpoint, thereby contributing to the in-situ exploration of lunar resources at mining scales.