Moving Target Detection in Multi-Static GNSS-Based Passive Radar Based on Multi-Bernoulli Filter
Abstract
:1. Introduction
2. MsGBPR System and Its Signal Model
2.1. Geometry of MsGBPR and Moving Target Echo Model
2.2. 2-D Coherent Integration Map Results of Moving Target
3. Moving Target Detection Based on Modified Multi-Bernoulli Filter
3.1. Multi-Bernoulli RFS and Multi-Bernoulli Filter
3.2. Multi-Beroulli Filtering for Target Detection in MsGBPR
3.2.1. Target Model, Measurement Model and Likelihood Ratio Function in MsGBPR
3.2.2. PMB Filter
3.2.3. ICMB Filter
3.3. Modified ICMB Filter with SNR Online Estimation
3.3.1. Online SNR Estimation
3.3.2. SMC Implementation of Modified Iterated-Corrector Multi-Bernoulli Filter
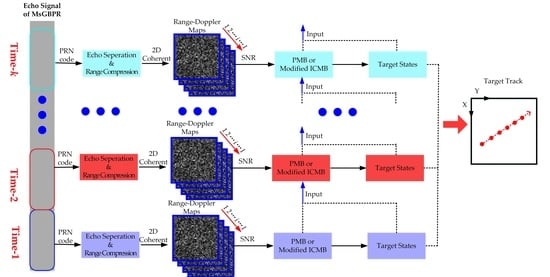
3.4. Moving Target Detection Framework
4. Experiments and Results
5. Discussion
5.1. Performance Evaluation
5.2. Improvement in Computational Efficiency
6. Preliminary Experimental Results with GPS Signals
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zavorotny, V.U.; Gleason, S.; Cardellach, E.; Camps, A. Tutorial on Remote Sensing Using GNSS Bistatic Radar of Opportunity. IEEE Geosci. Remote Sens. Mag. 2014, 2, 8–45. [Google Scholar] [CrossRef] [Green Version]
- Antoniou, M.; Cherniakov, M. GNSS-based bistatic SAR: A signal processing view. EURASIP J. Adv. Signal Process. 2013, 2013, 98. [Google Scholar] [CrossRef]
- Cherniakov, M. Bistatic Radar: Emerging technology, Chapter 9: Passive Bistatic SAR with GNSS Transimitters; Wiley: New York, NY, USA, 2008. [Google Scholar]
- Jin, S.; Cardellach, E.; Xie, F. GNSS Remote Sensing: Theory, Methods and Applications; Springer: New York, NY, USA, 2014. [Google Scholar]
- He, X.; Cherniakov, M.; Zeng, T. Signal detectability in SS-BSAR with GNSS non-cooperative transmitter. IEE Proc.-Radar Sonar Navig. 2005, 152, 124–132. [Google Scholar] [CrossRef]
- Liu, F.; Antoniou, M.; Zeng, Z.; Cherniakov, M. Coherent change detection using passive GNSS-based BSAR: Experimental proof of concept. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4544–4555. [Google Scholar] [CrossRef]
- Zeng, T.; Ao, D.; Hu, C.; Zhang, T.; Liu, F.; Tian, W.; Lin, K. Multiangle BSAR imaging based on BeiDou-2 navigation satellites: Experiments and preliminary results. IEEE Trans. Geosci. Remote Sens. 2015, 53, 5760–5773. [Google Scholar] [CrossRef]
- Ma, H.; Antoniou, M.; Pastina, D.; Santi, F.; Pieralice, F.; Bucciarelli, M.; Cherniakov, M. Maritime Moving Target Indication Using Passive GNSS-based Bistatic Radar. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 115–130. [Google Scholar] [CrossRef]
- Suberviola, I.; Mayordomo, I.; Mendizabal, J. Experimental Results of Air Target Detection with a GPS Forward-Scattering Radar. IEEE Geosci. Remote. Sens. Lett. 2011, 9, 47–51. [Google Scholar] [CrossRef]
- Hu, C.; Liu, C.; Wang, R.; Chen, L.; Wang, L. Detection and SISAR Imaging of Aircrafts Using GNSS Forward Scatter Radar: Signal Modeling and Experimental Validation. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 2077–2093. [Google Scholar] [CrossRef]
- Zeng, H.; Wang, P.; Chen, J.; Liu, W.; Ge, L. A Novel General Imaging Formation Algorithm for GNSS-Based Bistatic SAR. Sensors 2016, 16, 294. [Google Scholar] [CrossRef] [PubMed]
- Zhou, X.; Chen, J.; Wang, P.; Zeng, H.; Fang, Y.; Men, Z.; Liu, W. An Efficient Imaging Algorithm for GNSS-R Bi-static SAR. Remote Sens. 2019, 11, 2945. [Google Scholar] [CrossRef] [Green Version]
- Liu, F.F.; Fan, X.Z.; Zhang, L.Z.; Zhang, T.; Liu, Q.H. GNSS-based SAR for urban area imaging: Topology optimization and experimental confirmation. Int. J. Remote Sens. 2019, 40, 4668–4682. [Google Scholar] [CrossRef]
- Zeng, H.; Chen, J.; Wang, P.; Yang, W.; Liu, W. 2-D Coherent Integration Processing and Detecting of Aircrafts Using GNSS-based Passive Radar. Remote Sens. 2018, 10, 1164. [Google Scholar] [CrossRef] [Green Version]
- Pastina, D.; Santi, F.; Pieralice, F.; Buccciarelli, M.; Ma, H.; Tzagkas, D.; Antouiou, M.; Cherniakov, M. Maritime Moving Target Long Time Integration for GNSS-Based Passive Bistatic Radar. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 3060–3083. [Google Scholar] [CrossRef] [Green Version]
- Chen, X.; Tharmarasa, R.; Kirubarajan, T. Multitarget Multisensory Tracking; Academic Press Library in Signal Processing, Elsevier: New York, NY, USA, 2014; pp. 759–812. [Google Scholar]
- Mahler, R. Statistical Multisource-Multitarget Information Fusion; Artech House: Norwood, MA, USA, 2007. [Google Scholar]
- Mahler, R. Advances in Statistical Multisource-Multitarget Information Fusion; Artech House: Norwood, MA, USA, 2014. [Google Scholar]
- Mahler, R. Multitarget Bayes filtering via first-order multitarget moments. IEEE Trans. Aerosp. Electron. Syst. 2003, 39, 1152–1178. [Google Scholar] [CrossRef]
- Mahler, R. PHD filters of higher order in target number. IEEE Trans. Aerosp. Electron. Syst. 2007, 43, 1523–1543. [Google Scholar] [CrossRef]
- Vo, B.-T.; Vo, B.-N.; Cantoni, A. The cardinality balanced multi-target multi-Bernoulli filter and its implementations. IEEE Trans. Signal Process. 2009, 57, 409–423. [Google Scholar]
- Si, W.; Zhu, H.; Qu, Z. Multi-sensor Poisson multi-Bernoulli filter based on partitioned measurements. IET Radar Sonar Navig. 2020, 14, 860–869. [Google Scholar] [CrossRef]
- Vo, B.-T.; Vo, B.-N. Labeled random finite sets and multi-object conjugate priors. IEEE Trans. Signal Process. 2013, 61, 3460–3475. [Google Scholar] [CrossRef]
- Vo, B.-N.; Vo, B.-T.; Phung, D. Labeled random finite sets and the Bayes multi-target tracking filter. IEEE Trans. Signal Process. 2014, 62, 6554–6567. [Google Scholar] [CrossRef] [Green Version]
- Knoedler, B.; Broetje, M.; Koch, W. A particle filter for track-before-detect in GSM passive coherent location. In Proceedings of the IEEE Radar Conference, Boston, MA, USA, 22–26 April 2019; pp. 1–6. [Google Scholar]
- Mallick, M.; Krishnamurthy, V.; Vo, B.-N. Track-Before-Detect Techniques in Integrated Tracking, Classification, and Sensor Management: Theory and Applications; Wiley-IEEE: New York, NY, USA, 2012; pp. 311–362. [Google Scholar]
- Vo, B.-N.; Vo, B.-T.; Pham, N.-T.; Suter, D. Joint detection and estimation of multiple objects from image observations. IEEE Trans. Signal Process. 2010, 58, 5129–5141. [Google Scholar] [CrossRef]
- Hoseinnezhad, R.; Vo, B.-N.; Vo, B.-T. Visual tracking in background subtracted image sequences via multi-Bernoulli filtering. IEEE Trans. Signal Process. 2013, 61, 392–397. [Google Scholar]
- Gao, H.; Li, J. Detection and Tracking of a Moving Target Using SAR Images with the Particle Filter-Based Track-Before Detect Algorithm. Sensors 2014, 14, 10829–10845. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pham, N.T.; Huang, W.; Ong, S.H. Multiple sensor multiple object tracking with GMPHD filter. In Proceedings of the IEEE 10th International Conference Information Fusion, Québec, QC, Canada, 9–12 July 2007; pp. 1–7. [Google Scholar]
- Mahler, R. Approximate multisensor CPHD and PHD filters. In Proceedings of the International Conference Information Fusion, Edinburgh, UK, 26–29 July 2010; pp. 1–8. [Google Scholar]
- Uney, M.; Clark, D.E.; Julier, S.J. Distributed fusion of PHD filters via exponential mixture densities. IEEE J. Sel. Topics Signal Process. 2013, 7, 521–531. [Google Scholar] [CrossRef] [Green Version]
- Guldogan, M.B. Consensus Bernoulli filter for distributed detection and tracking using multi-static Doppler shifts. IEEE Signal Process. Lett. 2014, 24, 672–676. [Google Scholar] [CrossRef]
- Yi, W.; Jiang, M.; Hoseinnezhad, R.; Wang, B. Distributed multisensory fusion using generalised multi-Bernoulli densities. IEEE Trans. Signal Process. 2016, 11, 434–443. [Google Scholar]
- Fantacci, C.; Vo, B.-N.; Vo, B.-T.; Battistelli, G.; Chisci, L. Robust fusion for multisensor multiobject tracking. IEEE Signal Process. Lett. 2018, 25, 640–644. [Google Scholar] [CrossRef]
- Ong, J.; Kim, D.; Nordholm, S. Multi-sensor Multi-target Tracking Using Labelled Random Finite Set with Homography Data. In Proceedings of the International Conference on Control, Automation and Information Sciences, Chengdu, China, 24–27 October 2019; pp. 1–7. [Google Scholar]
- Saucan, A.; Coates, M.; Rabbat, M. A Multisensor Multi-Bernoulli Filter. IEEE Trans. Signal Process. 2017, 65, 5495–5509. [Google Scholar] [CrossRef] [Green Version]
- Vo, B.-N.; Vo, B.-T.; Beard, M. Multi-Sensor Multi-Object Tracking with the Generalized Labeled Multi-Bernoulli Filter. IEEE Trans. Signal Process. 2019, 67, 5952–5967. [Google Scholar] [CrossRef] [Green Version]
- Yi, W.; Li, S.; Wang, B.; Hoseinnezhad, R.; Kong, L. Computationally Efficient Distributed Multi-Sensor Fusion with Multi-Bernoulli Filter. IEEE Trans. Signal Process. 2020, 68, 241–256. [Google Scholar] [CrossRef] [Green Version]
- Kim, D.Y.; Vo, B.-N.; Vo, B.-T.; Jeon, M. A labeled random finite set online multi-object tracker for video data. Pattern Recognit. 2019, 90, 377–389. [Google Scholar] [CrossRef]
- Nannuru, S.; Coates, M. Hybrid multi-Bernoulli and CPHD filters for superpositional sensors. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 2847–2863. [Google Scholar] [CrossRef]
- Gostar, A.K.; Hoseinnezhad, R.; Bab-Hadiashar, A. Multi-Bernoulli sensor control via minimization of expected estimation errors. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 1762–1773. [Google Scholar] [CrossRef] [Green Version]
- Gostar, A.K.; Hoseinnezhad, R.; Bab-Hadiashar, A. Robust multi-Bernoulli sensor selection for multi-target tracking in sensor networks. IEEE Signal Process. Lett. 2013, 20, 1167–1170. [Google Scholar] [CrossRef]
- Nagappa, S.; Clark, D. On the ordering of the sensors in the iterated-corrector probability hypothesis density (PHD) filter. In Proceedings of the SPIE—The International Society for Optical Engineering, Orlando, FL, USA, 5 May 2011; Volume 8050, p. 80500M. [Google Scholar]
- Mahler, R. The multisensor PHD filter: II. Erroneous solution via Poissonmagic. In Proceedings of the SPIE—The International Society for Optical Engineering, Orlando, FL, USA, 11 May 2009; p. 73360D. [Google Scholar]
- Moreira, A.; Prats-Iraola, P.; Younis, M.; Krieger, G.; Hainsek, I.; Papathanassiou, K.P. A tutorial on synthetic aperture radar. IEEE Geosci. Remote Sens. Mag. 2013, 1, 6–43. [Google Scholar] [CrossRef] [Green Version]
- Skolnik, M. Introduction to Radar Systems; McGraw-Hill: New York, NY, USA, 2001. [Google Scholar]
- Olivares, J.; Martin, P.; Valero, E. A simple approximation for the modified Bessel function of zero order I 0(x). J. Phys. Conf. 2018, 1043, 012003. [Google Scholar] [CrossRef] [Green Version]
- Fang, Y.; Atkinson, G.; Sayin, A.; Chen, J.; Wang, P.; Antoniou, M.; Cherniakov, M. Improved Passive SAR Imaging With DVB-T Transmissions. IEEE Trans. Geosci. Remote Sens. 2020, 58, 5066–5076. [Google Scholar] [CrossRef] [Green Version]
- Garry, J.L.; Baker, C.J.; Smith, G.E. Evaluation of Direct Signal Suppression for Passive Radar. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3786–3799. [Google Scholar] [CrossRef]


















| Parameters | Values | Parameters | Values |
|---|---|---|---|
| Wavelength | 0.19 m | SVN #2 Position | (−17,745.0, 1835.5, 13,077.3) km |
| Sampling Rate | 5.0 MHz | SVN #2 Velocity | (2229.2, −519.2, 2058.0) m/s |
| Target Position | (140, 0, 5) km | SVN #10 Position | (10,232.9, −15,519.5, 12,420.5) km |
| Target Velocity | (−30, 100, 0) m/s | SVN #10 Velocity | (190.2, −2114.0, −1798.6) m/s |
| Map Frames | 20 | SVN #18 Position | (6818.7, −6090.4, 18,620.3) km |
| Target Appears | frame-5 | SVN #18 Velocity | (1654.7, −2019.3, −926.3) m/s |
| Target Disappears | frame-16 | SNRk,1, SNRk,2, SNRk,3 | 8, 9, 10 dB |
| Case 1 | Case 2 | Case 3 | Case 4 | Case5 | Case 6 | Case 7 | |
|---|---|---|---|---|---|---|---|
| Nf_s × Nr_s | 1 × 1 | 3 × 3 | 5 × 5 | 7 × 7 | 9 × 9 | 11 × 11 | Nf × Nr |
| Power ratio | 46.7% | 68.9% | 87.4% | 94.5% | 95.3% | 95.6% | 100% |
| Computation Time 1 | 36.86 s | 38.99 s | 41.33 s | 43.88 s | 46.65 s | 50.72 s | 260.05 s |
| Detected frame rate 2 | 51.9% | 73.2% | 95.7% | 98.6% | 99.4% | 99.7% | 99.8% |
| Parameters | Values | Parameters | Values |
|---|---|---|---|
| Wavelength | 0.19 m | Satellite information | SVN # 12, #25 |
| Signal Bandwidth | 2.046 MHz | Satellite signal | L1 |
| Sampling rate | 6.2 MHz | Antenna gain | 10 dB |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, H.; Chen, J.; Wang, P.; Liu, W.; Zhou, X.; Yang, W. Moving Target Detection in Multi-Static GNSS-Based Passive Radar Based on Multi-Bernoulli Filter. Remote Sens. 2020, 12, 3495. https://doi.org/10.3390/rs12213495
Zeng H, Chen J, Wang P, Liu W, Zhou X, Yang W. Moving Target Detection in Multi-Static GNSS-Based Passive Radar Based on Multi-Bernoulli Filter. Remote Sensing. 2020; 12(21):3495. https://doi.org/10.3390/rs12213495
Chicago/Turabian StyleZeng, HongCheng, Jie Chen, PengBo Wang, Wei Liu, XinKai Zhou, and Wei Yang. 2020. "Moving Target Detection in Multi-Static GNSS-Based Passive Radar Based on Multi-Bernoulli Filter" Remote Sensing 12, no. 21: 3495. https://doi.org/10.3390/rs12213495
APA StyleZeng, H., Chen, J., Wang, P., Liu, W., Zhou, X., & Yang, W. (2020). Moving Target Detection in Multi-Static GNSS-Based Passive Radar Based on Multi-Bernoulli Filter. Remote Sensing, 12(21), 3495. https://doi.org/10.3390/rs12213495