A Novel Machine Learning Approach to Estimate Grapevine Leaf Nitrogen Concentration Using Aerial Multispectral Imagery

Abstract

Assessment of the nitrogen status of grapevines with high spatial, temporal resolution offers benefits in fertilizer use efficiency, crop yield and quality, and vineyard uniformity. The primary objective of this study was to develop a robust predictive model for grapevine nitrogen estimation at bloom stage using high-resolution multispectral images captured by an unmanned aerial vehicle (UAV). Aerial imagery and leaf tissue sampling were conducted from 150 grapevines subjected to five rates of nitrogen applications. Subsequent to appropriate pre-processing steps, pixels representing the canopy were segmented from the background per each vine. First, we defined a binary classification problem using pixels of three vines with the minimum (low-N class) and two vines with the maximum (high-N class) nitrogen concentration. Following optimized hyperparameters configuration, we trained five machine learning classifiers, including support vector machine (SVM), random forest, XGBoost, quadratic discriminant analysis (QDA), and deep neural network (DNN) with fully-connected layers. Among the classifiers, SVM offered the highest F1-score (82.24%) on the test dataset at the cost of a very long training time compared to the other classifiers. Alternatively, QDA and XGBoost required the minimum training time with promising F1-score of 80.85% and 80.27%, respectively. Second, we transformed the classification into a regression problem by averaging the posterior probability of high-N class for all pixels within each of 150 vines. XGBoost exhibited a slightly larger coefficient of determination (R² = 0.56) and lower root mean square error (RMSE) (0.23%) compared to other learning methods in the prediction of nitrogen concentration of all vines. The proposed approach provides values in (i) leveraging high-resolution imagery, (ii) investigating spatial distribution of nitrogen across a vine’s canopy, and (iii) defining spatial zones for nitrogen application and smart sampling.

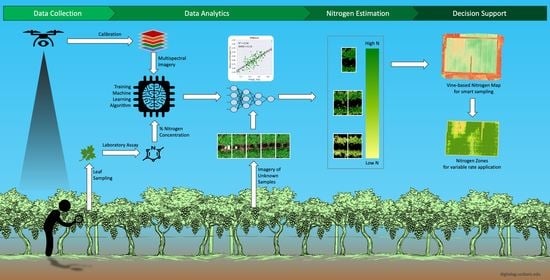
1. Introduction

The United States of America is the seventh largest table grape (Vitis vinifera L.) producing country in the world with 100 million 9 kg-boxes produced annually since 2012. Approximately 99% of the USA’s table grapes are produced in California, primarily in the southern San Joaquin Valley (SJV) [1]. One of the most common table grape cultivars in the SJV, and worldwide, is Flame Seedless [1]. Production of Flame Seedless, like other table grapes, is particularly capital-intensive, so it is imperative to maximize yield and quality to ensure profitability [2]. An important factor that contributes to grape yield and quality is vine mineral nutrition [3,4]. In SJV vineyards, nitrogen (N) is the mineral element that most often needs to be supplemented by fertilization [5]. Insufficient N limits vine vigor [6,7]. On the other hand, unnecessary application of N fertilizers needlessly increases the production cost, may cause unintended nutrient imbalances, contributes to environmental contamination [8]), stimulates excess vegetative growth, and reduces grape quality [9]. In fact, excessive application of nitrogen to crop plants has led to significant nitrate groundwater pollution in the SJV [10]. To help prevent further nitrate contamination to groundwater, growers in the SJV are required to implement nitrogen management plans.

Laboratory analyses of plant tissue samples can help determine if supplemental fertilizer treatments are necessary and are thus a fundamental component of N management plans [11]. Petioles are the most commonly sampled tissue of grapevines, but leaf blades may be used instead [11]. Tissue nutrient content changes markedly over the course of each season, hence samples are collected at particular growth stages to facilitate the comparison of data collected in other seasons or different locations. Bloom (anthesis) is the earliest standard sample collection time, and petioles or leaf blades collected at bloom are generally considered a reliable indicator of grapevine nutrient status and are thus widely used by commercial growers [12]. The collection of tissue samples is laborious, the analyses are relatively expensive, and care must be taken to ensure the samples collected are representative of the management area [4].

The increased availability and affordability of unmanned aerial and ground vehicles and advanced non-contact sensing technologies (e.g., hyper/multispectral sensors) has prompted research on remote sensing as a complimentary or alternative approach for estimating nitrogen status in specialty crops such as grape [4,13], apple [14], citrus [15], and almond [16]. An effective remote sensing protocol might offer some advantages over conventional testing, particularly with respect to spatial resolution and cost. For example, remote sensing could potentially reveal spatial variation of N status in grapevines, which can assist in identifying hot spots for smart sampling (i.e., directed sampling) and generating precise maps to develop a variable rate N fertilization program. However, the use of remote sensing for N estimation in crops has been constrained by issues associated with data analysis, such as overfitting, the curse of dimensionality, and developing robust, scalable, and generalizable predictive models. These large image-based datasets, often having high spatial, spectral, and temporal resolution, may require more sophisticated data analytics techniques to fully capitalize on the data, whereas conventional methods have previously relied on spectral indices [17].

Spectral indices have some significant limitations as analytical tools. For instance, normalized difference vegetation index (NDVI) saturates when vegetation coverage is dense [18], and atmospherically resistant vegetation index (ARVI) saturates when chlorophyll concentration reaches a certain level [19]. Previous studies have recommended a wide range of spectral indices and electromagnetic regions for predicting nitrogen content in crops. Pacheco-Labrador et al. [20] summarized more than 80 spectral indices from the literature for N content estimation. They achieved a strong coefficient of determination (R² = 0.76) between a spectral index composed of three spectral bands (1310, 1720, and 730 nm) and leaf nitrogen concentration in Holm oak. In addition, they identified red edge as a region with a high correlation to leaf N concentration. A number of studies reported electromagnetic regions suitable for N estimation including shortwave infrared (SWIR) [21], green, red edge, and near-infrared [20], visible region, mainly blue region [22], blue, green, and red edge [23], and red edge position [24]. While red edge has been frequently suggested as one of the most relevant spectral regions, Hansen and Schjoerring [22] questioned the importance of red edge as it was not identified as a significant band related to the N content of two winter wheat cultivars in their study. After calculating all possible normalized ratio indices for wavebands between 350 and 2200 nm aimed at predicting N content of five species, Ferwerda et al. [25] did not identify an optimal normalized ratio index that correlated well with the N content of five plant species. Considering the limitations of spectral indices, there is a need for advanced data analytics techniques to develop mathematical predictive models through harnessing the power of big data and computer processing.

The emergence of advanced machine learning techniques, along with high-performance computational power, has provided new opportunities to translate image-based datasets into novel insights. In agriculture, machine learning and deep learning have been recently implemented to analyze images captured for various applications, such as biotic stress detection [26,27], abiotic stress detection [28,29], nitrogen estimation [30,31], spectral features selection for high-throughput phenotyping [32], weed detection [33,34] and yield prediction [17,35].

Although the capability of machine learning has been verified in the agricultural domain, its full potential has been restricted by the limited number of ground truth data while developing a robust and generalizable predictive model demands a large and diverse dataset to capture the inherent large spatial and temporal variability in complex biological problems. Ground truth data collection is generally expensive, labor-intensive, and time-consuming. In addition, collecting ground truth data in agriculture often requires destructive experiments, like tissue sampling for nitrogen content measurements. A limited number of ground truth data confines the efficient use of advanced machine learning algorithms because it limits the tuning of the model’s hyperparameter and learning of the model’s parameters. Configuration of hyperparameters and parameters of a model is required for developing an underlying function that effectively maps the input variables to the desired output variables and maintains its performance on unseen datasets.

This study was motivated by the desire to develop a data-driven, decision-support tool to facilitate grapevine nitrogen management. The overarching goal of this study was to leverage high-resolution aerial multispectral imagery and advanced machine learning techniques to develop robust predictive models for grapevine nitrogen estimation at the bloom (anthesis) stage when tissue sampling is often performed. The specific objectives were to (i) develop predictive models through the optimized configuration of hyperparameters and parameters for accurate nitrogen concentration estimation at bloom, (ii) compare the performance of trained models in pixel-based binary classification and in vine-based prediction of nitrogen concentration, and (iii) investigate the spatial distribution of nitrogen across a canopy through pixel-based soft classification (i.e., calculating the posterior probabilities of classes).

2. Materials and Methods

2.1. Experimental Site

The research was conducted in a commercial table grape vineyard near Kingsburg, California. Vitis vinifera L. cv. Flame Seedless table grapes grafted onto Freedom rootstock were planted in 2012. Vine and row spacing was 1.83 and 3.66 m, respectively. The vines were trained to quadrilateral cordons and supported by a 3.05 m wide, Y-shaped, open gable trellis system.

All vines within the experimental portion of the vineyard were subjected to regular cultural practices performed by the grower with the exception of nitrogen fertilization. Vines in the study area were not fertilized or received different amounts of N as part of an N fertilization trial. Specifically, the effects of three levels of N (0, 19.2, or 48 g/vine) and two levels of split applications (2 versus 10 applications/season) were tested in a split-plot design where the level of N was the main plot factor (replicated five times), and the number of split applications was the subplot factor. This design required a total of 30 plots (3 levels of N × 2 split application treatments × 5 replications), each containing five individual vines, resulting in a study with 150 vines. Due to the combination of main plot factors (levels of N) and subplot factors (levels of split applications), at bloom, the time tissue samples were collected, the various plots had received a fraction of the total seasonal amount of N to be applied. Depending on the N and split application treatments to which the plots were assigned, the vines had received 0.0, 3.9, 9.6, 9.7, or 24.2 g N/vine (Figure 1A). The differential application of N affected leaf N concentration, which made the site an appropriate place to evaluate the potential of remote sensing to estimate leaf N concentration of table grapes.

Leaf tissue samples were collected from each of the five vines within each experimental plot immediately after aerial imagery at bloom. We collected one shoot at random from each of the 150 vines. Entire shoots were thoroughly rinsed in deionized water, and all of the leaf blades on each shoot were clipped from their petioles with shears, dried in a forced-air oven, ground into a fine powder, and then submitted to a commercial laboratory (Dellavalle Laboratory, Inc., Fresno, CA, USA) for determination of total N using the automated combustion method [36]. Nitrogen concentration values are expressed as a percentage of leaf dry weight. We followed a similar protocol except that the vine that each shoot was collected from was noted and considered a separate sample.

2.2. Airborne Multispectral Imaging System

The images were collected with the RedEdge 3 camera system (MicaSense, Inc., Seattle, WA, USA), which simultaneously captures five discrete spectral bands, including blue, green, red, red edge, and near-infrared. The field of view of the lens for all bands was 47.2 degrees. The size of the images was 1280 × 960 pixels, and they were saved with 16-Bit TIFF.

Table 1. Specification of MicaSense RedEdge 3 multispectral camera.

Bands	Center Wavelength (nm)	Bandwidth FWHM *
Blue	475	20
Green	560	20
Red	668	10
Red Edge	717	10
Near-infrared	840	40

* full width at half maximum.

summarizes the specification of the multispectral camera.

2.3. Aerial Imagery Campaign

Multispectral images were collected from the experimental plots during the bloom stage on 8 May 2019. The multispectral camera system was mounted on the dual downward gimbal mount of DJI Matrice 210 (Shenzhen, China) UAV using a 3D-printed mounting bracket. The multispectral images were captured individually from each single plot in a hovering state at an altitude about 15 m above ground level using the camera’s manual capture functionality through the WIFI interface to achieve sufficient spatial resolution (about 1 cm/pixel) for minimizing the number of mixed pixels. An automatic exposure setting was used during aerial multispectral imagery to leverage the sensor’s full dynamic range while avoiding saturation. The images were captured around solar noon with clear sky conditions.

2.4. Pre-Processing of Multispectral Images

A python-based framework called Micasense_preprocessing (version 1.0.0) was developed to automate all pre-processing steps, including radiometric calibration, unwarping (removing lens distortion for better image alignment), and bands alignments [37].

At the first step of radiometric calibration, raw images were converted to radiance to account for sensor-dependent factors such as gain, exposure setting, and vignette effects [17]. The Micasense_preprocessing uses information embedded in the header file of images for radiance conversion. Afterwards, the radiance images were converted to reflectance to account for the time-dependent factor, which is mainly variation in the intensity of incident light. The Micasense_preprocessing converted the radiance images to reflectance using incoming irradiance measured by a five-band incident light sensor integrated with the camera. The incident light sensor was mounted on the top of the aircraft using a 3D-printed mounting bracket while pointing upward to measure downwelling irradiance at each band per each captured image. In addition, the Micasense_preprocessing unwarped the images, aligned, and cropped each image to the common frame among all five bands.

2.5. Grapevine’s Canopy Segmentation

Two markers were placed on top of the first and last vine’s trunk in each plot to facilitate the identification of each plot extent. Afterwards, the extent of each vine within a plot was determined based on the markers’ location, spatial resolution (~1 cm/pixel), and vines spacing (1.83 m). Lastly, pixels representing the canopy were segmented from the background using a binary mask obtained from applying empirical thresholds on the excess green index (EGI) and NDVI (i.e., multiplying EGI and NDVI binary masks) [29] (Figure 1B). The canopy pixels located in the shaded area were removed during the segmentation process.

2.6. Analysis of Multispectral Dataset

Prediction of nitrogen at the vine-scale was essentially a regression problem in which we have a continuous output variable (i.e., nitrogen concentration). While we had a single value for nitrogen concentration per a given vine, there were thousands of pixels (i.e., samples) for each vine. One common approach is to average across all of the pixels for an individual vine to generate one feature vector (i.e., spectral response) per each output. Although this approach is widely used to address ill-matched problems, when there is only one output variable representing several samples, it can be a naïve solution because it ignores the variability of N concentrations within vines. This spatial variability, however, can be revealed by using an appropriate approach for analysis of high-resolution imagery.

In the first step of the analysis, a binary classification problem was defined at the pixel level to leverage the large number of pixels obtained through high-resolution imagery. In addition, this approach enabled us to investigate the distribution of nitrogen concentration across the top of the canopy. However, since the finest resolution at which nitrogen management decisions can be made is at the vine scale, we converted the pixel-based soft classification problem into a vine-based regression problem. The details of the proposed methodology are described hereinafter.

2.6.1. Training Machine Learning Classifiers

Based on the nitrogen concentration measured through tissue sampling for each vine, we defined two classes, low-N class and high-N class, such that a balanced dataset was generated with an approximately equal number of observations per each class. The low-N class entailed three vines (n = 42,604 pixels) with the minimum amount of nitrogen concentration, and the high-N class comprised two vines (n = 41,817 pixels) with the maximum amount of nitrogen concentration among all 150 vines (Figure 2A). Therefore, the matrix of features had 84,421 rows (i.e., pixels) and five columns (i.e., spectral bands), and the target array with the length of 84,421 contained the class labels (low-N or high-N) corresponding to each of the samples. The averaged spectral response of low-N and high-N classes are presented in Figure 2B.

After shuffling the dataset, about 10% of the data from each class was held out as a test dataset (4190 pixels for high-N and 4253 pixels for low-N class) for an unbiased evaluation of the prediction models, and the rest of the dataset (90%) was used for hyperparameter tuning and learning the model’s parameters.

The training dataset was standardized using the z-score technique such that each new feature had a zero-mean and unit-variance distribution. The mean and standard deviation of the training dataset was used for standardizing the test dataset [17].

In this study, we implemented five machine learning algorithms, including support vector machine (SVM), random forest, XGBoost, quadratic discriminant analysis (QDA), and deep neural network (DNN) with fully-connected layers. These classifiers were selected to examine various types of classifiers in terms of objective function, interpretability, scalability, sensitivity to outliers and noise, and ability to handle collinearity among the input features.

All models were developed in Python (version 3.7.3) using the scikit-learn library (version 0.22) [38], XGBoost library (version 0.90) [39], and TensorFlow library (version 2.1.0) [40].

2.6.2. Hyperparameter Optimization

The performance of machine learning models is largely influenced by the configuration of their internal parameters, so-called hyperparameters [41]. The aim of optimizing hyperparameters, which should be defined upfront by model developers, is to identify an optimal set of hyperparameters that offers the best performance on a validation dataset based on a desired validation metric such as F1-score or prediction error. Through hyperparameter optimization, as a key step in the development process of machine learning models, we attempt to develop a model that could generalize its performance on an unseen test dataset.

The most widely used approaches for optimizing hyperparameters have been grid and random search, among which random search tends to outperform [42]. However, grid and random search suffer from ignoring the past results observed during previous search iteration; hence they are inefficient in terms of required processing time to explore search space. Recently, the Bayesian optimization approach has been applied for hyperparameter tuning of machine learning models [43,44]. Using this approach, the history of previously evaluated trials is leveraged to strategically navigate the next hyperparameter search in search space in a more time-efficient manner. It has been shown that hyperparameter optimization techniques based on Bayesian optimization could significantly outstrip random search in terms of lower validation error and required computation time [43,45].

In this study, we utilized Tree Parzen Estimator [43], a similar method to Bayesian optimization, yet faster [46]. An optimal set of hyperparameters for each machine learning classifier was identified using the Optuna library (version 1.3.0) [47] in python. This library is a define-by-run application programming interface (API) that provides an automated framework to dynamically search hyperparameter space for the identification of an optimal set of hyperparameters through strategic searching and pruning method [47]. The list of hyperparameters optimized for each classifier is presented in

Table A1. List of hyperparameters, search space, and optimal values per each classifier. Optimized configuration of hyperparameters was identified using five-fold cross validation in Optuna library (version 1.3.0) in python (version 3.7.3).

Classifier	Hyperparameters	Search Space Domain	Optimal Parameter
support vector machine (SMV)	“kernel”	(“poly”, ”rbf”, “sigmoid”)	“rbf”
	“C”	(1 × 10−2, 1 × 102)	52.07
	“gamma”	(1 × 10−3, 1 × 100)	0.21
discriminant analysis	“classifier”	(QDA, LDA)	QDA
	“reg_param” (QDA)	(0, 1 × 10−3)	5.27 × 10−7
random forest	“n_estimators”	(100, 1000)	496
	“criterion”	(“gini”, “entropy”)	“entropy”
	“min_samples_split”	(2, 100)	38
	“min_samples_leaf”	(2, 50)	3
	“max_features”	(2, 5)	2
	“max_depth”	(10, 1000)	110
	“bootstrap”	(True, False)	TRUE
XGBoost	“num_boost_round”	(100, 1000)	292
	“learning_rate”	(0.01, 0.5)	0.45
	“feature_fraction”	(0.1, 1.0)	0.9
	“subsample”	(0.1, 1.0)	0.94
	“booster”	(“gbtree”, “gblinear”, “dart”)	“gbtree”
	“lambda”	(1 × 10−8, 1.0)	1.90 × 10−4
	“alpha”	(1 × 10−8, 1.0)	3.60 × 10−7
	“max_depth”	(1, 9)	9
	“eta”	(1 × 10−8, 1.0)	0.02
	“gamma”	(1 × 10−8, 1.0)	3.28 × 10−5
	“grow_policy”	(“depthwise”, “lossguide”)	“lossguide”
deep neural network (DNN)	“n_hidden_layers”	(1, 10)	6
	“weight_decay”	(1 × 10−10, 1 × 10−3)	4.44 × 10−8
	“activation”	(“relu”, “sigmoid”, “tanh”)	“tanh”
	“n_units_in_hidden_layers”	(4, 10)	(6, 6, 5, 6, 6, 5)
	“optimizer”	(“RMSprop”, “Adam”, “SGD”)	“Adam”
	“learning_rate”	(1 × 10−5, 1 × 10−1)	4.38 × 10−3
	“batch_size_power”	(5, 9)	25

.

2.7. Comparing Classifiers on Test Dataset

The performance of classifiers was evaluated on the test dataset using several metrics such as F1-score, precision, recall, and area under the curve (AUC) in the receiver operating characteristics curve [48]. In addition, the performance of the classifiers was also compared using a 10-fold cross-validation (CV) on the training dataset. The required time for training and testing the classifiers was also recorded to compare the scalability of the models.

2.8. Transforming Classification into Regression

The ultimate goal for developing machine learning predictive models was to predict the nitrogen concentration at the vine-scale at which fertilizer decision and application are performed. The classifiers were developed to return posterior class probability—a soft classification approach rather than a hard-binary classification. The posterior probability of high-N given spectral data ($P(high\_N|X)$) for all pixels representing each of 150 vines was averaged to calculate the probability of high-N at the vine scale. Then, the coefficient of determination between $P(high\_N|X)$ and the measured nitrogen concentration was computed for each predictive model. Root mean square error (RMSE) was also calculated as another metric for prediction error. SVM was omitted for this step as the standard SVM does not offer per-class posterior probability [49]. In this approach, the performance of models trained on pixels of five vines was evaluated on a large dataset, including vines with N concentration distribution outside of the training dataset composed of pixels of five vines with extreme nitrogen concentration.

The entire process from data collection to data analysis and interpretation is summarized as a flowchart in Figure A1.

3. Results

3.1. Bands Pairwise Correlation

Patterns and relationships between the features (spectral bands) for the two classes (low-N and high-N) were investigated through exploratory data analysis (EDA) in which bands were mutually plotted against each other in the shape of a rectangular 5 × 5 matrix (Figure 3).

The upper triangle of the grid in Figure 3 illustrates the scatter plots of pixels in two-dimensional feature spaces, each spanned by two bands. These scatter plots provide information about the correlation between bands, distribution of the pixels, and the extent of low-N class deviation from high-N class. In general, spectral bands exhibited positive correlation mutually. The scatter plots in Figure 3 indicate that red edge has a strong correlation with both near-infrared (NIR) and red bands, whereas green band exhibits relatively less correlation with other bands. In addition, scatter plots depict how different pair-band combinations differentiated low-N and high-N classes. For instance, NIR and green bands, which were less correlated, offered better discrimination of the two classes compared to the other pairs. It also appears that the NIR-RedEdge scatter plot is the other feature space in which the two classes are more separated while there is a strong correlation between the NIR and red edge bands.

Pixels representing low-N class tend to scatter more in the feature space, indicating more variation among pixels. Alternatively, pixels of the high-N class tend to cluster with less variation, generating denser area in the scatter plots. However, the regions with a higher density per each class are not noticeable in the scatter plots due to a large number of pixels and a high degree of overlapping. Therefore, the bivariate kernel density estimate (KDE) is shown in the lower triangle of the grid in Figure 3. The bivariate KDE plots illustrate the variability of the underlying probability density function of each class across the two-dimensional feature space spanned by two bands. While the scatter plots provide information about the distribution of the pixels from the two classes, the bivariate KDE plots demonstrate the probability density of the pixels per each class—regions with higher probability density are shown with a darker color in Figure 3. Similar to the scatter plots, bivariate KDE plots indicate the positive correlation between spectral bands as the major axis of the ellipsoid in pairwise plots has a positive slope.

The diagonal plots in Figure 3 show the underlying probability density function of two classes estimated with univariate KDE—a nonparametric technique with a Gaussian kernel function. The univariate KDE plots provide insight into the reflectance pattern of pixels representing the two classes. For instance, the low-N pixels tended to reflect more in green and red bands, which explains why the leaves with low N concentration appear to have a light green-yellow color.

3.2. Hyperparameter Tuning

The goal of hyperparameter tuning was to assure an optimal set of the model’s hyperparameters that returns the best performance is used during the training step of the model. Figure 4 shows the variation of classification accuracy for SMV as a function of hyperparameter values for more than 100 trials, where the accuracy reached a plateau. For this dataset, the “radial basis function” tended to result in a higher accuracy; therefore, it was selected as the kernel for the SVM classifier. The optimal values for the regularization parameter (C = 52.07) and kernel coefficient (gamma = 0.21) were identified based on the SVM performance across the trials. The list of hyperparameters, search space domain per each hyperparameter, and the selected optimal hyperparameters are shown in Table A1 per each classifier.

3.3. Performance of Classifiers

The performance of five classifiers was examined in this study. Once the classifiers were trained on the training dataset ($n=\mathrm{75,978}$) with the optimal hyperparameters, their performance was evaluated on the test dataset ($n=8443$) using several metrics including F1-score, precision, recall, and area under the curve (AUC) in receiver operating characteristics (ROC) curve.

Table 2. Comparing the performance of classifiers on test (n = 8443) and training datasets (n = 75,978). The result of the training dataset was obtained using 10-fold cross-validation.

Classifier	Test Dataset							Training Dataset
	F1 1 (%)	Precision (%)	Recall (%)	AUC 2 (%)	Threshold 3	Training time (s)	Prediction time (s)	F1 –mean (%)	F1 StD 4
SVM	82.24	82.35	82.25	_	_	128.59	3.45	82.25	0.32
QDA	80.85	80.96	80.86	89.01	0.54	0.02	0.01	80.40	0.30
Random Forest	81.81	81.81	81.81	90.25	0.51	91.39	0.62	81.55	0.23
XGBoost	80.27	80.29	80.27	88.29	0.51	7.29	0.02	80.94	0.31
DNN	81.68	81.79	81.69	89.90	0.52	316.09	0.57	81.34	0.52
Ensemble	82.24	82.31	82.25	90.31	_	543.37	4.66	_	_

¹ Average of F1-scores weighted by samples of each class; ² Area under the curve in receiver operating characteristics curve; ³ Optimal decision threshold for classification; ⁴ Standard deviation of F1-score among 10 folds.

presents the performance of classifiers on the test dataset as well as the training dataset using a 10-fold cross-validation. Among the classifiers, SVM offered the best performance at the cost of long training time compared to the other classifiers. Alternatively, QDA and XGBoost required the minimum training time. While F1-mean and AUC provide information about the ability of the classifiers in learning from the training dataset and generalization on an unseen test dataset, the required time for training and testing of classifiers indicates the scalability of the classifiers to larger datasets. QDA needed a small fraction of a second (0.02 s) to return a promising F1-mean (80.85%), which was about 1.4% lower than the highest F1-mean obtained by SVM (82.24%). It should be noted that AUC was not calculated for SVM because the SVM classifier does not return the probability of belonging to classes for a given sample.

To aggregate the benefits of each classifier, an ensemble classifier was constructed by combining the prediction made by the classifiers. For a given test sample, all trained classifiers were used to predict its class label. Using the voting approach, a class label with the maximum of votes was assigned to the test sample. The ensemble classifier was not able to improve the performance of classification. This might suggest there are pixels in the test dataset that the majority of the classifiers were not able to classify them correctly; hence, the ensemble approach did not enhance the classification performance. For instance, some of the pixels in high-N class might present a very similar reflectivity to low-N class and vice versa.

The high F1-score averaged among the 10-folds of the training dataset and its low standard deviation across the folds for each classifier, indicated the performance of the classifiers was consistent regardless of which folds of samples were used as training and test datasets. In addition, it suggested a similar F1-score can be expected by deploying the trained classifiers using all training dataset to predict the class labels of the test dataset. This observation that the F1-scores obtained for 10-fold CV and test dataset were very close to one another might suggest the optimal hyperparameters were identified for each classifier.

3.4. Nitrogen Prediction of Vines

Once the classifiers had been trained on the training dataset using the optimal hyperparameters, they were utilized to predict the probability of high-N class for all pixels of other vines. The predicted probability values were then averaged across the pixels of a vine to compute one probability value ($P(high\_N|X)$) per each vine. Figure 5 shows the coefficient of determination ($R^2$) and root mean square error ($\mathrm{RMSE}$) for nitrogen prediction of four classifiers capable of predicting the class label as a probability. XGBoost exhibited a slightly larger coefficient of determination and lower RMSE compared to other learning methods in the prediction of N concentration of vines.

4. Discussion

4.1. Influence of Leaf Nitrogen Concentration on Spectral Characteristics

A mechanistic understanding of how incident light interacts with leaves of different N concentrations is required for a meaningful interpretation of remote sensing data, such as aerial multispectral images. In this study, the observed differences between the spectral responses of low-N and high-N classes might be the result of physiological changes, such as leaf chlorophyll concentration, which is correlated with the N concentration of fully expanded leaf blades [13].

4.1.1. Visible Bands (Blue, Green, and Red)

A healthy (i.e., non-stressed) leaf has a tendency to absorb a larger extent of incident light in blue and red bands for photosynthesis activities. Therefore, the higher reflectivity of low-N pixels in blue and red bands can be an indication of a decline in chlorophyll content. Compared to red band, the reflectivity of low-N class at blue band was less affected by the N concentration—a larger alteration was observed in the red band (Figure 2B and diagonal plots in Figure 3). This observation may suggest that chlorophyll in grape leaves, with high absorption at blue and red bands, was more sensitive to N deficiency compared with carotenoids, which have high absorption in blue regions. The ratio between carotenoid and chlorophyll has been previously reported to increase in plants under stress or with senescing leaves [50]. Based on this alteration in the relative ratio between carotenoid and chlorophyll, spectral indices such as the normalized pigments chlorophyll ratio index (NPCI) [51] and normalized difference plant senescence index (NDPSI) [17] have been developed to assess N deficiency in leaves and to segment senescent leaves in aerial imagery, respectively. In the green band, pixels representing low-N class tended to show a greater reflectance (Figure 2B and diagonal plots in Figure 3) in response to a decrease in leaf chlorophyll concentration [52,53].

4.1.2. Red Edge Band

Red edge is historically known to be an indirect estimator of plant N status as red edge position was shown to shift to a shorter wavelength in response to a decline in chlorophyll content [54,55], and chlorophyll content itself was shown to be correlated with N content in grapes [13,50]. Although an accurate calculation of red edge position is not possible in multispectral imaging due to its coarse spectral resolution, the higher reflectivity of low-N class in red and red edge suggests the red edge position has shifted towards shorter wavelengths (Figure 2B).

4.1.3. Near-Infrared Band

Healthy leaves tend to have a high reflectivity in near-infrared due to their internal cellular structure [56]. Pixels of low-N class tended to have lower reflectance in near-infrared band compared to the pixels representing the high-N class (Figure 2B). The reduction in near-infrared reflectance of leaves with low nitrogen concentration may indicate that the internal cellular structure of the leaves sustained damages as previous studies demonstrated the reflectance of leaves in near-infrared is largely influenced by leaf structure [57,58].

In summary, the near-infrared band exhibited the largest absolute difference between the spectral reflectance of low-N and high-N class, followed by the red edge, green, red, and blue bands. This is in agreement with a previous study that showed that near-infrared, red edge, and green bands have the highest coefficient of determination between leaf reflectance from 400 to 2500 nm and leaf nitrogen concentration in Holm oak [20]. However, if we sort the multispectral bands based on the absolute values of percentage difference $\left(\left|\frac{{\rho }_{hig{h}_N}-{\rho }_{lo{w}_N}}{{\rho }_{hig{h}_N}}\right|\times 100\right)$, the order will become green (10.41%), near-infrared (9.02%), red (8.63%), red edge (6.09%), and blue (2.61%).

4.2. Significance of the Proposed Data-Driven Method

Prediction of leaf N concentration was inherently a regression problem, which requires the prediction of a continuous variable (i.e., N concentration) given multiple input variables (i.e., multispectral images). One of the novel contributions of this study was to deploy machine learning classifiers for this type of regression problem. The process started with training supervised binary classifiers on pixels of vines with extreme N concentration. Once a classifier was trained with its optimal set of hyperparameters, it was utilized to predict N concentration of a given vine in the form of probability of belonging to either of classes (i.e., low-N or high-N).

The alternative approach was to train a regression algorithm for the direct prediction of N concentration at the vine scale. In this approach, the spectral response of pixels representing vine canopy should be averaged per vine to obtain one input feature vector per ground truth data, which was the vine’s N concentration measured through tissue sampling. Therefore, substantial spatial and spectral information is diminished through the averaging process across the thousands of pixels in a vine [17]. In addition, to train a robust regression algorithm for learning a complex problem such as nitrogen prediction, more substantial ground truth data are required in this approach since the total number of samples is limited to the number of vines, which was 150 in this study.

The proposed method in this study, on the other hand, offers several advantages which are discussed here.

4.2.1. Appropriate Use of High-Resolution Imagery

One of the benefits of the proposed framework is to leverage thousands of samples in the form of pixels attained through high-resolution aerial imagery. Although a dataset with a large number of samples, compared to the number of features, does not necessarily assure developing accurate learning models, it allows having (i) an adequate training dataset to develop a robust mapping function for mapping from an input space to an output space, (ii) a validation dataset with a sufficient number of samples to identify an optimal set of hyperparameters and better tuning the parameters of the learning model, and (iii) a test dataset with more diverse samples to reliably evaluate the generalization performance of the model.

The results demonstrated the efficiency in learning from large training data and the reliability of the trained models in predicting the class labels of unseen test samples. The high F1-mean and low F1-std achieved by the 10-fold CV on the training dataset indicated low bias and variance error, respectively (Table 2). Moreover, the F1-mean of CV can be used as an estimation for the expected model accuracy on unseen data. This was verified by the results obtained on the test dataset, indicating the generalization ability of the trained classifiers on new datasets. In addition, the promising regression results confirmed the validity of the proposed approach in predicting N concentration in grapevines.

4.2.2. Spatial Distribution of N Across the Vine’s Canopy

Nitrogen is a significant determinant for the photosynthetic activity of plants, and its distribution within the canopy is a key element of photosynthesis and carbon gain at the canopy level [59]. The pixel-based probability, ($P(high\_N|X) \mathrm{or}P(low\_N|X)$), estimated by the trained predictive models can assist in the mechanistic understanding of the N distribution at the surface of the canopy in a non-invasive and quantitative manner.

Figure 6A shows the distribution of the posterior probability of high-N class ($P(high\_N|X)$) at the pixel level, obtained by a XGBoost classifier and two widely used spectral indices, normalized difference vegetation index (NDVI) and normalized difference red edge index (NDRE), for two vines one with the lowest N concentration (2.41%) and the other with the highest N concentration (4.19%) among all vines. While the distribution of $P(high\_N|X)$ for the two vines are well-separated, there is a high degree of overlap between the distribution of NDVI and NDRE for these two vines with low and high N concentrations. This highlights the ability of the predictive models in distinguishing vines with low N concentrations from vines with high N concentrations.

Figure 6B illustrates pixel-based probability ($P(high\_N|X)$) obtained by XGBoost classifier along with NDVI and NDRE, represented with a colormap, for two plots with zero and 24.2 g applied nitrogen per vine. Figure 6B demonstrates how the results achieved by XGBoost could capture the variability of N across the plots—a vine with a high N concentration exhibits more dark green pixels, whereas a vine with low N concentration displays more light yellow pixels. Similar to the histograms, there is a distinct difference between the vines with low and high N concentration for the $P(high\_N|X)$ compared to NDVI and NDRE. In essence, machine learning algorithms provide a wider dynamic range, which is visually more appealing for human sensory comparison. Furthermore, machine learning can be used as a practical tool to spot hot zones with low nitrogen concentration in a large commercial orchard. Among the two indices, NDRE performed better in discrimination of the vines with extreme N concentration.

According to $P(high\_N|X)$ calculated for vines in the plot with 24.2 g of N applied per vine, pixels representing the leaves at the apical portion of the shoots (edge of the canopy toward the middle of the row) were classified as low-N, most probably because these are young leaves with less chlorophyll content than more mature leaves. Grapevine leaves at the shoot apex have been shown to have significantly lower chlorophyll and N (when expressed per unit leaf area) than those located further down the shoot (mid and basal positions) at bloom, however, the N concentration (expressed per unit dry weight) of the apical leaves are significantly greater than those of the more mature leaves [60]. In this study, pixels representing apical leaves in the high N plot (i.e., 24.2 g/vine) exhibited similar spectral responses to leaves with decreased N in the zero applied N plots, even though their N concentration may be high. This agrees with the conclusions of Friedel et al. [13] who reported a disconnect between chlorophyll and N in young grape leaves. Consequently, the predictive models classified the pixels representing apical leaves as the low-N class (Figure 6B).

4.2.3. Adjustable Decision Threshold for Spatial Zoning of Nitrogen

In this study, the optimal decision threshold for classifying low-N and high-N classes was calculated based on the maximum weighted F1-score. However, the proposed framework in this study offers flexibility in the discretion of decision thresholds to define N management zones according to various vineyard-specific conditions and management strategies. For example, in a conservative N management approach, large threshold values for $P(high\_N|X)$ can be defined to determine N management zones, aimed to assure minimum N stress. Alternatively, in an environmentally friendly approach, smaller threshold values can be defined to reduce the risk of environmental contamination caused by excessive N application. Therefore, in the proposed method, agronomic expert knowledge can be integrated with machine learning to define optimal N management zones.

4.2.4. Directed Sampling from Hot Spot in Vineyard

The proposed data-driven method can help growers collect tissue samples in a more intelligent and efficient manner. The descriptive N status map generated by the proposed method (similar to Figure 6) can be used to efficiently identify vines with a various N status aimed at directed sampling. The conventional random or grid sampling techniques, or sampling based on vineyard history, can be replaced by the directed sampling technique, which can provide insights into N spatial variability.

4.3. Limitation of Multispectral Imaging

As discussed above, young leaves with less chlorophyll may exhibit a spectral response similar to leaves with low N concentration. In addition, many other stresses or diseases can lead to chlorophyll degradation in leaves, resulting in spectral patterns similar to leaves with low N concentration [61]. For instance, leaves with water stress in grapevine may exhibit similar spectral characteristics to leaves suffering from N deficiency as they tend to have a lower reflectivity in near-infrared and higher reflectivity in red edge and red bands compared to well-irrigated leaves [62]. Therefore, multispectral imaging with a limited number of typical bands (blue, green, red, red edge, and near-infrared) may not serve as the best tool for N assessment, in particular for a commercial vineyard where other stress/diseases inducing chlorophyll degradation might be prevalent. In such cases, hyperspectral imaging may be used to identify the most informative spectral bands aimed at developing a custom-designed multispectral sensor for particular stress/disease detection, such as N deficiency in grapevines [32,63].

5. Conclusions

This study proposed an innovative method for the analysis of high-resolution aerial multispectral images captured at the bloom stage to assess nitrogen concentration in vines. A supervised binary classification problem was defined to, (i) benefit from a training machine learning on a larger dataset obtained through high-resolution imagery, (ii) provide insight on spatial variability of nitrogen concentration within a single vine as well as across the grape vineyard, and (iii) accommodate diverse points of view, benefit-oriented or environmental-oriented perspectives, in defining an optimal threshold for fertilizer management decisions. For this purpose, five commonly used machine learning classifiers were trained with an optimal set of hyperparameters. The highest F1-score (82.24%) on test dataset was achieved by SVM with maximum training time, whereas QDA and XGBoost required the minimum training time with promising F1-scores of 80.85% and 80.27%, respectively. Afterwards, we transformed the classification problem into a regression problem to predict N concentration at vine scale. Through implementing a soft classification approach, the posterior probability of high-N class given spectral data ($P(high\_N|X)$) for all pixels of a vine was averaged to be used as an indication of nitrogen concentration at vine scale. Among the predictive models, XGBoost performed slightly better in terms of coefficient of determination and RMSE in the prediction of nitrogen concentration. The findings of this study can offer immediate practical applications for sustainable nitrogen management, such as (i) providing insights on nitrogen variability in vineyards, which could be useful for variable rate management, (ii) identifying hot zones with low nitrogen content for a more informed and efficient tissue sampling. In addition, we investigated the impact of low nitrogen concentration on the spectral characteristics of leaves in five bands. Based on the percentage difference between the averaged spectral response of low-N and high-N class, the largest difference was observed for green, near-infrared, red, red edge, and blue. To identify the most informative bands for nitrogen estimation, a sensor, like a hyperspectral camera, with a higher spectral resolution, is required along with advanced feature selection techniques.