The Ultra-Short-Term Forecasting of Global Horizonal Irradiance Based on Total Sky Images
Abstract
:1. Introduction
2. Instruments and Data
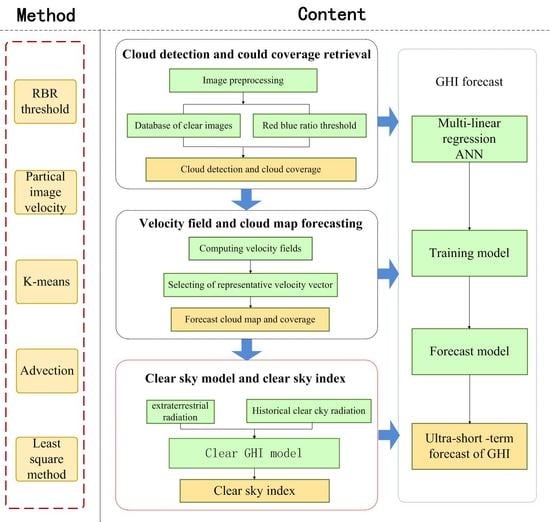
3. Methods and Results
3.1. Cloud Detection and Retrieve
3.2. Cloud Velocity and Cloud Map Forecasting
3.3. The Clear Sky Model and Clear Sky Index
3.4. Forecasting of GHI
3.4.1. Two Forecast Models of GHI
3.4.2. Evaluation of Forecast Models
3.4.3. Results of GHI Forecasting
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Haegel, N.M.; Margolis, R.; Buonassisi, T.; Feldman, D.; Froitzheim, A.; Garabedian, R.; Green, M.; Glunz, S.; Henning, H.-M.; Holder, B.; et al. Terawatt-scale photovoltaics: Trajectories and challenges. Science 2017, 356, 141–143. [Google Scholar] [CrossRef] [PubMed]
- Breyer, C.; Bogdanov, D.; Gulagi, A.; Aghahosseini, A.; Barbosa, L.S.; Koskinen, O.; Barasa, M.; Caldera, U.; Afanasyeva, S.; Child, M.; et al. On the role of solar photovoltaics in global energy transition scenarios. Prog. Photovolt. Res. Appl. 2017, 25, 727–745. [Google Scholar] [CrossRef]
- Wilson, G.M.; Al-Jassim, M.; Metzger, W.K.; Glunz, S.W.; Verlinden, P.; Xiong, G.; Mansfield, L.M.; Stanbery, B.J.; Zhu, K.; Yan, Y.; et al. The 2020 photovoltaic technologies roadmap. J. Phys. D Appl. Phys. 2020, 53, 493001. [Google Scholar] [CrossRef]
- IEA. 2020. Available online: https://www.iea.org/reports/solar-pv (accessed on 1 October 2020).
- Lave, M.; Kleissl, J. Solar variability of four sites across the state of Colorado. Renew. Energy 2010, 35, 2867–2873. [Google Scholar] [CrossRef] [Green Version]
- Li, F.; Chen, Z.; Cheng, C.; Duan, S. Review on Forecast Methods for Photovoltaic Power Generation. Adv. Clim. Chang. Res. 2011, 7, 136–142. [Google Scholar]
- Li, W.H.; He, X.N. Review of Nonisolated High-Step-Up DC/DC Converters in Photovoltaic Grid-Connected Applications. IEEE Trans. Ind. Electron. 2011, 58, 1239–1250. [Google Scholar] [CrossRef]
- Marchesoni-Acland, F.; Alonso-Suarez, R. Intra-day solar irradiation forecast using RLS filters and satellite images. Renew. Energy 2020, 161, 1140–1154. [Google Scholar] [CrossRef]
- Haupt, S.E.; Dettling, S.; Williams, J.K.; Pearson, J.; Jensen, T.; Brummet, T.; Kosovic, B.; Wiener, G.; McCandless, T.; Burghardt, C. Blending distributed photovoltaic and demand load forecasts. Sol. Energy 2017, 157, 542–551. [Google Scholar] [CrossRef]
- Zang, H.; Liu, L.; Sun, L.; Cheng, L.; Wei, Z.; Sun, G. Short-term global horizontal irradiance forecasting based on a hybrid CNN-LSTM model with spatiotemporal correlations. Renew. Energy 2020, 160, 26–41. [Google Scholar] [CrossRef]
- Kuhn, P.; Nouri, B.; Wilbert, S.; Prahl, C.; Kozonek, N.; Schmidt, T.; Yasser, Z.; Ramirez, L.; Zarzalejo, L.; Meyer, A.; et al. Validation of an all-sky imager-based nowcasting system for industrial PV plants. Prog. Photovolt. Res. Appl. 2017, 26, 608–621. [Google Scholar] [CrossRef]
- Hasenbalg, M.; Kuhn, P.; Wilbert, S.; Nouri, B.; Kazantzidis, A. Benchmarking of six cloud segmentation algorithms for ground-based all-sky imagers. Sol. Energy 2020, 201, 596–614. [Google Scholar] [CrossRef]
- Yanbo, S.; Zongci, Z.; Guangyu, S. The Progress in Variation of Surface Solar Radiation, Factors and Probable Climatic Effects. Adv. Earth Sci. 2008, 23, 915–923. [Google Scholar]
- Matuszko, D. Influence of the extent and genera of cloud cover on solar radiation intensity. Int. J. Clim. 2012, 32, 2403–2414. [Google Scholar] [CrossRef]
- Antonanzas, J.; Osorio, N.; Escobar, R.; Urraca, R.; Martinez-de-Pison, F.J.; Antonanzas-Torres, F. Review of photovoltaic power forecasting. Sol. Energy 2016, 136, 78–111. [Google Scholar] [CrossRef]
- Pfister, G.; McKenzie, R.L.; Liley, J.B.; Thomas, A.; Forgan, B.W.; Long, C.N. Cloud coverage based on all-sky imaging and its impact on surface solar irradiance. J. Appl. Meteorol. 2003, 42, 1421–1434. [Google Scholar] [CrossRef]
- Liou, K.-N. Introduction to Atmospheric Radiation; China Meteorological Press: Beijing, China, 2004; p. 494. [Google Scholar]
- Martin, L.; Zarzalejo, L.F.; Polo, J.; Navarro, A.; Marchante, R.; Cony, M. Prediction of global solar irradiance based on time series analysis: Application to solar thermal power plants energy production planning. Sol. Energy 2010, 84, 1772–1781. [Google Scholar] [CrossRef]
- Mellit, A.; Eleuch, H.; Benghanem, M.; Elaoun, C.; Pavan, A.M. An adaptive model for predicting of global, direct and diffuse hourly solar irradiance. Energy Conv. Manag. 2010, 51, 771–782. [Google Scholar] [CrossRef]
- Paoli, C.; Voyant, C.; Muselli, M.; Nivet, M.L. Forecasting of preprocessed daily solar radiation time series using neural networks. Sol. Energy 2010, 84, 2146–2160. [Google Scholar] [CrossRef] [Green Version]
- Voyant, C.; Muselli, M.; Paoli, C.; Nivet, M.L. Optimization of an artificial neural network dedicated to the multivariate forecasting of daily global radiation. Energy 2011, 36, 348–359. [Google Scholar] [CrossRef] [Green Version]
- Voyant, C.; Muselli, M.; Paoli, C.; Nivet, M.L. Numerical weather prediction (NWP) and hybrid ARMA/ANN model to predict global radiation. Energy 2012, 39, 341–355. [Google Scholar] [CrossRef] [Green Version]
- Perez, R.; Lorenz, E.; Pelland, S.; Beauharnois, M.; Van Knowe, G.; Hemker, K.; Heinemann, D.; Remund, J.; Müller, S.C.; Traunmüller, W.; et al. Comparison of numerical weather prediction solar irradiance forecasts in the US, Canada and Europe. Sol. Energy 2013, 94, 305–326. [Google Scholar] [CrossRef]
- Yagli, G.M.; Yang, D.; Srinivasan, D. Automatic hourly solar forecasting using machine learning models. Renew. Sustain. Energy Rev. 2019, 105, 487–498. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, S.; Zhang, W.; Peng, J.; Cai, Y. Multifactor spatio-temporal correlation model based on a combination of convolutional neural network and long short-term memory neural network for wind speed forecasting. Energy Convers. Manag. 2019, 185, 783–799. [Google Scholar] [CrossRef]
- Lorenz, E.; Hurka, J.; Heinemann, D.; Beyer, H.G. Irradiance Forecasting for the Power Prediction of Grid-Connected Photovoltaic Systems. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2009, 2, 2–10. [Google Scholar] [CrossRef]
- Perez, R.; Kivalov, S.; Schlemmer, J.; Hemker, K.; Renne, D.; Hoff, T.E. Validation of short and medium term operational solar radiation forecasts in the US. Sol. Energy 2010, 84, 2161–2172. [Google Scholar] [CrossRef]
- Mathiesen, P.; Kleissl, J. Evaluation of numerical weather prediction for intra-day solar forecasting in the continental United States. Sol. Energy 2011, 85, 967–977. [Google Scholar] [CrossRef] [Green Version]
- Calbo, J.; Sabburg, J. Feature extraction from whole-sky ground-based images for cloud-type recognition. J. Atmos. Ocean. Technol. 2008, 25, 3–14. [Google Scholar] [CrossRef] [Green Version]
- Chow, C.W.; Urquhart, B.; Lave, M.; Dominguez, A.; Kleissl, J.; Shields, J.; Washom, B. Intra-hour forecasting with a total sky imager at the UC San Diego solar energy testbed. Sol. Energy 2011, 85, 2881–2893. [Google Scholar] [CrossRef] [Green Version]
- Inman, R.H.; Pedro, H.T.C.; Coimbra, C.F.M. Solar forecasting methods for renewable energy integration. Prog. Energy Combust. Sci. 2013, 39, 535–576. [Google Scholar] [CrossRef]
- Marquez, R.; Coimbra, C.F.M. Intra-hour DNI forecasting based on cloud tracking image analysis. Sol. Energy 2013, 91, 327–336. [Google Scholar] [CrossRef]
- Quesada-Ruiz, S.; Chu, Y.; Tovar-Pescador, J.; Pedro, H.T.C.; Coimbra, C.F.M. Cloud-tracking methodology for intra-hour DNI forecasting. Sol. Energy 2014, 102, 267–275. [Google Scholar] [CrossRef]
- Yang, H.D.; Kurtz, B.; Nguyen, D.; Urquhart, B.; Chow, C.W.; Ghonima, M.; Kleissl, J. Solar irradiance forecasting using a ground-based sky imager developed at UC San Diego. Sol. Energy 2014, 103, 502–524. [Google Scholar] [CrossRef]
- Marquez, R.; Gueorguiev, V.G.; Coimbra, C.F.M. Forecasting of Global Horizontal Irradiance Using Sky Cover Indices. J. Sol. Energy Eng. Trans.-ASME 2013, 135, 5. [Google Scholar] [CrossRef] [Green Version]
- Chu, Y.H.; Li, M.Y.; Coimbra, C.F.M. Sun-tracking imaging system for intra-hour DNI forecasts. Renew. Energy 2016, 96, 792–799. [Google Scholar] [CrossRef]
- Du, J.; Min, Q.; Zhang, P.; Guo, J.; Yang, J.; Yin, B. Short-Term Solar Irradiance Forecasts Using Sky Images and Radiative Transfer Model. Energies 2018, 11, 1107. [Google Scholar] [CrossRef] [Green Version]
- Wang, F.; Xuan, Z.; Zhen, Z.; Li, Y.; Li, K.; Zhao, L.; Shafie-Khah, M.; Catalão, J.P. A minutely solar irradiance forecasting method based on real-time sky image-irradiance mapping model. Energy Convers. Manag. 2020, 220, 113075. [Google Scholar] [CrossRef]
- Voronych, O.; Höller, R.; Beck, G.L.; Traunmüller, W. Solar PV nowcasting based on skycamera observations. Adv. Sci. Res. 2019, 16, 7–10. [Google Scholar] [CrossRef] [Green Version]
- Cantor, A. Optics of the atmosphere--Scattering by molecules and particles. IEEE J. Quantum Electron. 1978, 14, 698–699. [Google Scholar] [CrossRef]
- Schade, N.H.; Macke, A.; Sandmann, H.; Stick, C. Enhanced solar global irradiance during cloudy sky conditions. Meteorol. Z. 2007, 16, 295–303. [Google Scholar] [CrossRef]
- Huo, J.; Lv, D. A method to retrieve the radiance from all-sky visible images. Acta Meteorol. Sin. 2010, 68, 800–807. [Google Scholar]
- Han, Y.; Song, J. An equivalent surface model of image distortion and the correction algorithm. Opt. Technol. 2005, 31, 122–124. [Google Scholar]
- Liou, K.-N. An Introduction to Atmospheric Radiation, 2nd ed.; Academic Press: San Diego, CA, USA, 2004; p. 259. [Google Scholar]
- Shields, J.E.; Johnson, R.W.; Koehler, T.L. Automated Whole Sky Imaging Systems for Cloud Field Assessment; Fourth Symposium on Global Change Studies: Boston, MA, USA; American Meteorological Society: Boston, MA, USA, 1993; pp. 228–231. [Google Scholar]
- Mori, N.; Chang, K.A. Introduction to MPIV. Available online: http://www.oceanwave.jp/softwares/mpiv (accessed on 8 October 2020).
- Chu, Y.H.; Pedro, H.T.C.; Coimbra, C.F.M. Hybrid intra-hour DNI forecasts with sky image processing enhanced by stochastic learning. Sol. Energy 2013, 98, 592–603. [Google Scholar] [CrossRef]
- Marquez, R.; Pedro, H.T.C.; Coimbra, C.F.M. Hybrid solar forecasting method uses satellite imaging and ground telemetry as inputs to ANNs. Sol. Energy 2013, 92, 176–188. [Google Scholar] [CrossRef]
- Sheng, P.; Mao, J.; Li, J.; Sang, J.; Pan, N. Atmospheric Physics; China Meteorological Press: Beijing, China, 2006; pp. 84–98. [Google Scholar]
- Cionco, R.G.; Soon, W.W.-H. Short-term orbital forcing: A quasi-review and a reappraisal of realistic boundary conditions for climate modeling. Earth-Sci. Rev. 2017, 166, 206–222. [Google Scholar] [CrossRef] [Green Version]
- Ineichen, P. Comparison of eight clear sky broadband models against 16 independent data banks. Sol. Energy 2006, 80, 468–478. [Google Scholar] [CrossRef] [Green Version]
- Kasten, F.; Czeplak, G. Solar and terrestrial radiation dependent on the amount and type of cloud. Sol. Energy 1980, 24, 177–189. [Google Scholar] [CrossRef]













| Model | Time Scale | RMSE | MAE | MBE | rRMSE | rMAE | rMBE | R |
|---|---|---|---|---|---|---|---|---|
| TLR | 0 min | 8.593 | 4.460 | 0.370 | 0.038 | 0.020 | 0.002 | 0.998 |
| 1 min | 46.732 | 26.479 | 0.279 | 0.203 | 0.115 | 0.001 | 0.95 | |
| 2 min | 64.119 | 38.595 | −1.107 | 0.278 | 0.167 | −0.005 | 0.91 | |
| 3 min | 83.427 | 49.840 | −4.934 | 0.347 | 0.208 | −0.021 | 0.86 | |
| 5 min | 117.063 | 71.094 | −7.650 | 0.502 | 0.305 | −0.033 | 0.83 | |
| BPN | 1 min | 16.070 | 8.649 | −0.971 | 0.069 | 0.037 | −0.004 | 0.993 |
| 2 min | 27.431 | 14.760 | −1.206 | 0.118 | 0.064 | −0.005 | 0.980 | |
| 3 min | 37.219 | 21.471 | 0.017 | 0.152 | 0.088 | 0.000 | 0.966 | |
| 5 min | 49.500 | 28.701 | −1.932 | 0.212 | 0.123 | −0.008 | 0.936 | |
| 10 min | 73.136 | 46.970 | −4.762 | 0.311 | 0.200 | −0.020 | 0.864 |
| Model | Time Scale | RMSE | MAE | MBE | rRMSE | rMAE | rMBE | R |
|---|---|---|---|---|---|---|---|---|
| TLR | 0 min | 33.320 | 15.906 | 2.411 | 0.117 | 0.056 | 0.008 | 0.996 |
| 1 min | 48.784 | 30.077 | 1.221 | 0.169 | 0.104 | 0.004 | 0.931 | |
| 2 min | 65.655 | 44.577 | 0.628 | 0.227 | 0.154 | 0.002 | 0.882 | |
| 3 min | 102.039 | 68.285 | −1.546 | 0.352 | 0.236 | −0.005 | 0.757 | |
| 5 min | 124.722 | 85.332 | −3.327 | 0.429 | 0.294 | −0.011 | 0.672 | |
| BPN | 1 min | 43.307 | 26.267 | −0.065 | 0.151 | 0.092 | 0.000 | 0.937 |
| 2 min | 56.867 | 36.142 | −2.368 | 0.198 | 0.126 | −0.008 | 0.893 | |
| 3 min | 81.953 | 54.740 | −0.672 | 0.286 | 0.191 | −0.002 | 0.801 | |
| 5 min | 97.350 | 63.719 | 4.313 | 0.338 | 0.221 | 0.015 | 0.742 | |
| 10 min | 124.594 | 89.594 | 2.770 | 0.430 | 0.309 | 0.010 | 0.555 |
| Model | Time Scale | RMSE | MAE | MBE | rRMSE | rMAE | rMBE | R |
|---|---|---|---|---|---|---|---|---|
| TLR | 0 min | 6.562 | 1.885 | −0.076 | 0.020 | 0.006 | 0.000 | 0.996 |
| 1 min | 32.690 | 14.152 | 0.958 | 0.096 | 0.042 | 0.003 | 0.931 | |
| 2 min | 54.270 | 24.522 | 2.736 | 0.164 | 0.074 | 0.008 | 0.882 | |
| 3 min | 49.692 | 24.503 | −4.380 | 0.149 | 0.074 | −0.013 | 0.757 | |
| 5 min | 58.799 | 30.687 | −6.170 | 0.176 | 0.092 | −0.018 | 0.672 | |
| BPN | 1 min | 47.604 | 27.184 | 0.368 | 0.173 | 0.099 | 0.001 | 0.944 |
| 2 min | 66.083 | 40.428 | −5.953 | 0.240 | 0.147 | −0.022 | 0.889 | |
| 3 min | 81.247 | 52.912 | −4.567 | 0.294 | 0.192 | −0.017 | 0.841 | |
| 5 min | 98.843 | 65.099 | −2.602 | 0.357 | 0.235 | −0.009 | 0.773 | |
| 10 min | 109.479 | 74.403 | −5.503 | 0.452 | 0.307 | −0.023 | 0.727 |
| Model | Time Scale | RMSE | MAE | MBE | rRMSE | rMAE | rMBE | R |
|---|---|---|---|---|---|---|---|---|
| TLR | 0 min | 8.579 | 2.973 | −1.494 | 0.026 | 0.009 | −0.005 | 0.999 |
| 1 min | 31.334 | 13.912 | −4.006 | 0.092 | 0.041 | −0.012 | 0.988 | |
| 2 min | 52.052 | 22.725 | −7.152 | 0.157 | 0.068 | −0.022 | 0.967 | |
| 3 min | 71.395 | 31.077 | −10.971 | 0.215 | 0.093 | −0.033 | 0.941 | |
| 5 min | 111.740 | 45.512 | −21.055 | 0.335 | 0.136 | −0.063 | 0.875 | |
| BPN | 1 min | 38.779 | 18.536 | 1.195 | 0.116 | 0.055 | 0.004 | 0.980 |
| 2 min | 53.112 | 26.449 | 0.922 | 0.158 | 0.079 | 0.003 | 0.963 | |
| 3 min | 55.241 | 27.653 | 2.119 | 0.165 | 0.083 | 0.006 | 0.961 | |
| 5 min | 57.718 | 30.609 | 0.817 | 0.172 | 0.091 | 0.002 | 0.956 | |
| 10 min | 81.365 | 50.763 | 1.780 | 0.321 | 0.401 | 0.010 | 0.895 |
| Model | Time Scale | RMSE | MAE | MBE | rRMSE | rMAE | rMBE |
|---|---|---|---|---|---|---|---|
| TLR | 0 min | 14.26 | 6.31 | 0.30 | 0.05 | 0.023 | 0.001 |
| 1 min | 39.89 | 21.16 | −0.39 | 0.14 | 0.076 | −0.001 | |
| 2 min | 59.02 | 32.60 | −1.22 | 0.21 | 0.116 | −0.004 | |
| 3 min | 76.64 | 43.43 | −5.46 | 0.27 | 0.15 | −0.018 | |
| 5 min | 103.08 | 58.16 | −9.55 | 0.36 | 0.21 | −0.031 | |
| BPN | 1 min | 38.78 | 18.54 | 1.20 | 0.12 | 0.055 | 0.004 |
| 2 min | 53.11 | 26.45 | 0.92 | 0.16 | 0.079 | 0.003 | |
| 3 min | 55.24 | 27.65 | 2.20 | 0.17 | 0.083 | 0.006 | |
| 5 min | 57.72 | 30.61 | 0.82 | 0.17 | 0.091 | 0.002 | |
| 10 min | 81.37 | 50.76 | 1.78 | 0.32 | 0.401 | 0.010 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, J.; Lv, Q.; Gao, X. The Ultra-Short-Term Forecasting of Global Horizonal Irradiance Based on Total Sky Images. Remote Sens. 2020, 12, 3671. https://doi.org/10.3390/rs12213671
Jiang J, Lv Q, Gao X. The Ultra-Short-Term Forecasting of Global Horizonal Irradiance Based on Total Sky Images. Remote Sensing. 2020; 12(21):3671. https://doi.org/10.3390/rs12213671
Chicago/Turabian StyleJiang, Junxia, Qingquan Lv, and Xiaoqing Gao. 2020. "The Ultra-Short-Term Forecasting of Global Horizonal Irradiance Based on Total Sky Images" Remote Sensing 12, no. 21: 3671. https://doi.org/10.3390/rs12213671
APA StyleJiang, J., Lv, Q., & Gao, X. (2020). The Ultra-Short-Term Forecasting of Global Horizonal Irradiance Based on Total Sky Images. Remote Sensing, 12(21), 3671. https://doi.org/10.3390/rs12213671