Random Sample Fitting Method to Determine the Planetary Boundary Layer Height Using Satellite-Based Lidar Backscatter Profiles
Abstract
:1. Introduction
2. Site and Data
2.1. Site
2.2. Radiosonde
2.3. Atmospheric Emitted Radiance Interferometer
2.4. CALIPSO/CALIOP
3. Methods
3.1. Ideal Profile Fitting (IPF) Method
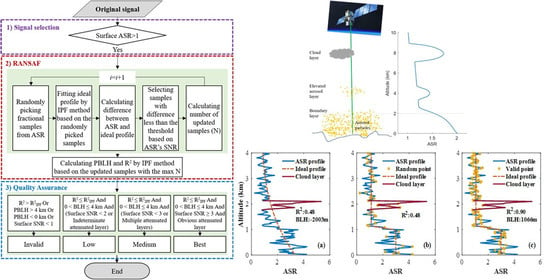
3.2. Random Sample Fitting (RANSAF) Method
- (1)
- Single selection
- (2)
- Random sample fitting
- (3)
- Quality assurance
3.3. Other Traditional Methods
3.3.1. MSD
3.3.2. MGD
3.3.3. WCT
4. Results and Analysis
4.1. Simulated Experiment
4.2. Measured Experiment
4.2.1. Determining PBLH under Effects of Strong Backscatter Layers
4.2.2. Determining PBLH under Low SNR Conditions
4.2.3. Determining PBLHs from a CALIPSO Trajectory
- (1)
- Case with strong backscatter layer
- (2)
- Case with low SNRs
5. Discussion
5.1. Multiple Attenuated Layers
5.2. Indeterminate Attenuated Layer
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Stull, R.B. An Introduction to Boundary Layer Meteorology; Springer Science and Business Media LLC: Berlin/Heidelberg, Germany, 1988; Volume 13. [Google Scholar]
- Zhang, Y.; Seidel, D.J.; Zhang, S. Trends in Planetary Boundary Layer Height over Europe. J. Clim. 2013, 26, 10071–10076. [Google Scholar] [CrossRef]
- Kong, W.; Yi, F. Convective boundary layer evolution from lidar backscatter and its relationship with surface aerosol concentration at a location of a central China megacity. J. Geophys. Res. Atmos. 2015, 120, 7928–7940. [Google Scholar] [CrossRef]
- Wang, W.; Mao, F.; Zou, B.; Guo, J.; Wu, L.; Pan, Z.; Zang, L. Two-stage model for estimating the spatiotemporal distribution of hourly PM1.0 concentrations over central and east China. Sci. Total Environ. 2019, 675, 658–666. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Mao, F.; Du, L.; Pan, Z.; Gong, W.; Fang, S. Deriving Hourly PM2.5 Concentrations from Himawari-8 AODs over Beijing–Tianjin–Hebei in China. Remote Sens. 2017, 9, 858. [Google Scholar] [CrossRef] [Green Version]
- McGrath-Spangler, E.L.; Denning, A.S. Global seasonal variations of midday planetary boundary layer depth from CALIPSO space-borne LIDAR. J. Geophys. Res. Atmos. 2013, 118, 1226–1233. [Google Scholar] [CrossRef]
- Tsaknakis, G.; Papayannis, A.; Kokkalis, P.; Amiridis, V.; Kambezidis, H.D.; Mamouri, R.E.; Georgoussis, G.; Avdikos, G. Inter-comparison of lidar and ceilometer retrievals for aerosol and Planetary Boundary Layer profiling over Athens, Greece. Atmos. Meas. Tech. 2011, 4, 1261–1273. [Google Scholar] [CrossRef] [Green Version]
- Cramer, O.P. Potential Temperature Analysis for Mountainous Terrain. J. Appl. Meteorol. 1972, 11, 44–50. [Google Scholar] [CrossRef]
- Seidel, D.J.; Ao, C.O.; Li, K. Estimating climatological planetary boundary layer heights from radiosonde observations: Comparison of methods and uncertainty analysis. J. Geophys. Res. Space Phys. 2010, 115, 16113. [Google Scholar] [CrossRef] [Green Version]
- Korhonen, K.; Giannakaki, E.; Mielonen, T.; Pfüller, A.; Laakso, L.; Vakkari, V.; Baars, H.; Engelmann, R.; Beukes, J.P.; Van Zyl, P.G.; et al. Atmospheric boundary layer top height in South Africa: Measurements with lidar and radiosonde compared to three atmospheric models. Atmos. Chem. Phys. Discuss. 2014, 14, 4263–4278. [Google Scholar] [CrossRef] [Green Version]
- Zhang, W.; Guo, J.; Miao, Y.; Liu, H.; Zhang, Y.; Li, Z.; Zhai, P. Planetary boundary layer height from CALIOP compared to radiosonde over China. Atmos. Chem. Phys. Discuss. 2016, 16, 9951–9963. [Google Scholar] [CrossRef] [Green Version]
- Hocke, K.; Kämpfer, N.; Gerber, C.; Mätzler, C. A complete long-term series of integrated water vapour from ground-based microwave radiometers. Int. J. Remote Sens. 2011, 32, 751–765. [Google Scholar] [CrossRef]
- Wang, Z.; Cao, X.; Zhang, L.; Notholt, J.; Zhou, B.; Liu, R.; Zhang, B. Lidar measurement of planetary boundary layer height and comparison with microwave profiling radiometer observation. Atmos. Meas. Tech. 2012, 5, 1965–1972. [Google Scholar] [CrossRef] [Green Version]
- Coen, M.C.; Praz, C.; Haefele, A.; Ruffieux, D.; Kaufmann, P.; Calpini, B. Determination and climatology of the planetary boundary layer height above the Swiss plateau by in situ and remote sensing measurements as well as by the COSMO-2 model. Atmos. Chem. Phys. Discuss. 2014, 14, 13205–13221. [Google Scholar] [CrossRef] [Green Version]
- Winker, D.; Hunt, W.H.; McGill, M.J. Initial performance assessment of CALIOP. Geophys. Res. Lett. 2007, 34, L19803. [Google Scholar] [CrossRef] [Green Version]
- Liu, B.; Ma, Y.; Liu, J.; Gong, W.; Wang, W.; Zhang, M. Graphics algorithm for deriving atmospheric boundary layer heights from CALIPSO data. Atmos. Meas. Tech. 2018, 11, 5075–5085. [Google Scholar] [CrossRef] [Green Version]
- Kim, S.-W.; Berthier, S.; Raut, J.-C.; Chazette, P.; Dulac, F.; Yoon, S.-C. Validation of aerosol and cloud layer structures from the space-borne lidar CALIOP using a ground-based lidar in Seoul, Korea. Atmos. Chem. Phys. Discuss. 2008, 8, 3705–3720. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Huang, J.; Chen, B.; Zhou, T.; Yan, H.; Jin, H.; Huang, Z.; Zhang, B. Comparisons of PBL heights derived from CALIPSO and ECMWF reanalysis data over China. J. Quant. Spectrosc. Radiat. Transf. 2015, 153, 102–112. [Google Scholar] [CrossRef]
- Su, T.; Li, J.; Li, C.; Xiang, P.; Lau, A.K.-H.; Guo, J.; Yang, D.; Miao, Y. An intercomparison of long-term planetary boundary layer heights retrieved from CALIPSO, ground-based lidar, and radiosonde measurements over Hong Kong. J. Geophys. Res. Atmos. 2017, 122, 3929–3943. [Google Scholar] [CrossRef]
- Leventidou, E.; Zanis, P.; Balis, D.; Giannakaki, E.; Pytharoulis, I.; Amiridis, V. Factors affecting the comparisons of planetary boundary layer height retrievals from CALIPSO, ECMWF and radiosondes over Thessaloniki, Greece. Atmos. Environ. 2013, 74, 360–366. [Google Scholar] [CrossRef]
- Steyn, D.G.; Baldi, M.; Hoff, R.M. The Detection of Mixed Layer Depth and Entrainment Zone Thickness from Lidar Backscatter Profiles. J. Atmos. Ocean. Technol. 1999, 16, 953–959. [Google Scholar] [CrossRef]
- Baars, H.; Ansmann, A.; Engelmann, R.; Althausen, D. Continuous monitoring of the boundary-layer top with lidar. Atmos. Chem. Phys. Discuss. 2008, 8, 7281–7296. [Google Scholar] [CrossRef] [Green Version]
- Eresmaa, N.; Karppinen, A.; Joffre, S.M.; Räsänen, J.; Talvitie, H. Mixing height determination by ceilometer. Atmos. Chem. Phys. Discuss. 2006, 6, 1485–1493. [Google Scholar] [CrossRef] [Green Version]
- Luo, T.; Yuan, R.; Wang, Z. Lidar-based remote sensing of atmospheric boundary layer height over land and ocean. Atmos. Meas. Tech. 2014, 7, 173–182. [Google Scholar] [CrossRef] [Green Version]
- Hayden, K.L.; Anlauf, K.G.; Hoff, R.M.; Strapp, J.W.; Bottenheim, J.W.; Wiebe, H.A.; Froude, F.A.; Martin, J.B.; Steyn, D.G.; McKendry, I.G. The vertical chemical and meteorological structure of the boundary layer in the Lower Fraser Valley during Pacific ’93. Atmos. Environ. 1997, 31, 2089–2105. [Google Scholar] [CrossRef]
- Perrone, M.; Romano, S. Relationship between the planetary boundary layer height and the particle scattering coefficient at the surface. Atmos. Res. 2018, 213, 57–69. [Google Scholar] [CrossRef]
- Mao, F.; Gong, W.; Shalei, S.; Zhu, Z. Determination of the boundary layer top from lidar backscatter profiles using a Haar wavelet method over Wuhan, China. Opt. Laser Technol. 2013, 49, 343–349. [Google Scholar] [CrossRef]
- Brooks, I.M. Finding Boundary Layer Top: Application of a Wavelet Covariance Transform to Lidar Backscatter Profiles. J. Atmos. Ocean. Technol. 2003, 20, 1092–1105. [Google Scholar] [CrossRef] [Green Version]
- Hicks, M.; Sakai, R.; Joseph, E. The Evaluation of a New Method to Detect Mixing Layer Heights Using Lidar Observations. J. Atmos. Ocean. Technol. 2015, 32, 2041–2051. [Google Scholar] [CrossRef]
- Cohn, S.A.; Angevine, W.M. Boundary Layer Height and Entrainment Zone Thickness Measured by Lidars and Wind-Profiling Radars. J. Appl. Meteorol. 2000, 39, 1233–1247. [Google Scholar] [CrossRef]
- Thorsen, T.J.; Fu, Q.; Newsom, R.K.; Turner, D.D.; Comstock, J.M. Automated Retrieval of Cloud and Aerosol Properties from the ARM Raman Lidar. Part I: Feature Detection. J. Atmos. Ocean. Technol. 2015, 32, 1977–1998. [Google Scholar] [CrossRef]
- Atmospheric Radiation Measurement (ARM) User Facility. Updated Hourly. Balloon-Borne Sounding System (SONDEWNPN). 2007-01-01 to 2019-12-31, Southern Great Plains (SGP) Central Facility, Lamont, OK (C1); Holdridge, D., Ritsche, M., Coulter, R., Kyrouac, J., Keeler, E., Eds.; ARM Data Center: Washington, DC, USA, 2020. [CrossRef]
- Liu, S.; Liang, X.-Z. Observed Diurnal Cycle Climatology of Planetary Boundary Layer Height. J. Clim. 2010, 23, 5790–5809. [Google Scholar] [CrossRef]
- Su, T.; Li, Z.; Kahn, R. A new method to retrieve the diurnal variability of planetary boundary layer height from lidar under different thermodynamic stability conditions. Remote Sens. Environ. 2020, 237, 111519. [Google Scholar] [CrossRef]
- Zhang, Y.; Gao, Z.; Li, D.; Li, Y.; Zhang, N.; Zhao, X.; Chen, J. On the computation of planetary boundary-layer height using the bulk Richardson number method. Geosci. Model Dev. 2014, 7, 2599–2611. [Google Scholar] [CrossRef] [Green Version]
- Feltz, W.F.; Smith, W.L.; Howell, H.B.; Knuteson, R.; Woolf, H.; Revercomb, H.E. Near-Continuous Profiling of Temperature, Moisture, and Atmospheric Stability Using the Atmospheric Emitted Radiance Interferometer (AERI). J. Appl. Meteorol. 2003, 42, 584–597. [Google Scholar] [CrossRef]
- Winker, D.; Vaughan, M.A.; Omar, A.; Hu, Y.; Powell, K.A.; Liu, Z.; Hunt, W.H.; Young, S.A. Overview of the CALIPSO Mission and CALIOP Data Processing Algorithms. J. Atmos. Ocean. Technol. 2009, 26, 2310–2323. [Google Scholar] [CrossRef]
- Liu, Z.; Vaughan, M.A.; Winker, D.; Kittaka, C.; Getzewich, B.; Kuehn, R.; Omar, A.; Powell, K.; Trepte, C.; Hostetler, C. The CALIPSO Lidar Cloud and Aerosol Discrimination: Version 2 Algorithm and Initial Assessment of Performance. J. Atmos. Ocean. Technol. 2009, 26, 1198–1213. [Google Scholar] [CrossRef]
- Vaughan, M.; Winker, D.M.; Powell, K. CALIOP Algorithm Theoretical Basis Document, Part 2: FEATURE Detection and Layer Properties Algorithms; NASA Langley Research Center: Hampton, VA, USA, 2005.
- Earth Resources Observation and Science (EROS) Center. GTOPO30 Documentation (README File). USGS: Reston, VA, USA, 1997. Available online: https://www.usgs.gov/science-explorer-results?es=GTOPO30+ (accessed on 19 March 2020).
- NOAA; NASA; USAF. US Standard Atmosphere, 1976; National Oceanic and Atmospheric Administration: Washington, DC, USA, 1976; Volume 76.
- Fischler, M.A.; Bolles, R.C. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Compton, J.C.; Delgado, R.; Berkoff, T.A.; Hoff, R.M. Determination of Planetary Boundary Layer Height on Short Spatial and Temporal Scales: A Demonstration of the Covariance Wavelet Transform in Ground-Based Wind Profiler and Lidar Measurements. J. Atmos. Ocean. Technol. 2013, 30, 1566–1575. [Google Scholar] [CrossRef]
- Ma, X.; Wang, C.; Han, G.; Ma, Y.; Li, S.; Gong, W.; Chen, J. Regional Atmospheric Aerosol Pollution Detection Based on LiDAR Remote Sensing. Remote Sens. 2019, 11, 2339. [Google Scholar] [CrossRef] [Green Version]
- Guo, J.; Liu, B.; Gong, W.; Shi, L.; Zhang, Y.; Ma, Y.; Zhang, J.; Chen, T.; Bai, K.; Stoffelen, A.; et al. Technical Note: First comparison of wind observations from ESA’s satellite mission Aeolus and ground-based Radar wind profiler network of China. Atmos. Chem. Phys. Discuss. 2020, 2020, 1–36. [Google Scholar] [CrossRef]












Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, L.; Pan, Y.; Wang, W. Random Sample Fitting Method to Determine the Planetary Boundary Layer Height Using Satellite-Based Lidar Backscatter Profiles. Remote Sens. 2020, 12, 4006. https://doi.org/10.3390/rs12234006
Du L, Pan Y, Wang W. Random Sample Fitting Method to Determine the Planetary Boundary Layer Height Using Satellite-Based Lidar Backscatter Profiles. Remote Sensing. 2020; 12(23):4006. https://doi.org/10.3390/rs12234006
Chicago/Turabian StyleDu, Lin, Ya’ni Pan, and Wei Wang. 2020. "Random Sample Fitting Method to Determine the Planetary Boundary Layer Height Using Satellite-Based Lidar Backscatter Profiles" Remote Sensing 12, no. 23: 4006. https://doi.org/10.3390/rs12234006
APA StyleDu, L., Pan, Y., & Wang, W. (2020). Random Sample Fitting Method to Determine the Planetary Boundary Layer Height Using Satellite-Based Lidar Backscatter Profiles. Remote Sensing, 12(23), 4006. https://doi.org/10.3390/rs12234006