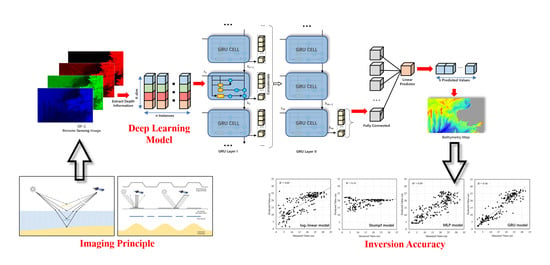
Underwater Topography Inversion in Liaodong Shoal Based on GRU Deep Learning Model
Abstract
:1. Introduction
2. Data and Research Area
2.1. Research Area
2.2. Datasets
2.3. Data Preprocessing
2.3.1. Radiance Conversion
2.3.2. Atmospheric Correction
2.3.3. Geometric Correction
- (1)
- Orthorectification: refers to the aid of the digital elevation model (DEM). Each pixel in the image is corrected to make the image meet the requirements of orthographic projection. The purpose is to eliminate the influence of topography or the deformation caused by the orientation of the camera and to generate a plane Orthophoto Image.
- (2)
- Geometric correction: in this study, the geographic coordinates were corrected using the intersection of longitude and latitude network in the sea chart.
2.3.4. Water Depth Point Information
3. Optical Remote Sensing Imaging Mechanism of Underwater Topography
3.1. Imaging Mechanism in the Clear Sea Area
3.2. Imaging Mechanism in the Turbid or Relatively Deep-Sea Area
4. Model and Algorithm
4.1. Analysis of the Unified Inversion Model of Water Depth in a Composite Environment
4.2. GRU-Based Underwater Topography Optical Remote Sensing Inversion Algorithm
5. Results and Discussion
5.1. Accuracy Evaluation Method
- RMSE (root mean square error)
- MAE (mean absolute error)
- MRE (mean relative error)In the above three formulas, and are the inverted water depth value and the true water depth value of the th point, respectively, and is the total number of water depth points participating in the accuracy evaluation.
- R2 (determination coefficient)
5.2. Overall Accuracy Evaluation of Underwater Topography
5.3. Segmented Accuracy Evaluation of Underwater Topography
5.4. Influence Analysis of Model Parameters
5.4.1. Network Structure
5.4.2. Optimizer Selection
5.4.3. Batch Size
5.4.4. Number of Iterations
5.5. Influence of Control Points Proportion
5.6. Spatial Analysis of Underwater Topography Inversion by Remote Sensing
5.7. Considerations about the Input Data for Model
- (a)
- GF-1 satellite is a multi-spectral satellite with a spatial resolution of 16 m and has four optical bands, which cannot make full use of the sequential feature learning ability of the GRU model. If reliable hyperspectral data are introduced to future work, it is believed that better results will be obtained.
- (b)
- The Liaodong Shoal area has a relatively high sediment concentration; the sea water is muddy. Considering that some information such as chlorophyll concentration, yellow substance concentration and suspended substance concentration have considerable influence on the bathymetric optical signal, if these factors can be introduced into the future work, it is believed that the inversion performance of this method can be further improved. At the same time, the dimension of input data will be higher and more suitable for deep learning models.
- (c)
- The effects of passive optical remote sensing depth inversion are often limited by the quality of control points and check points. Generally, the sources of bathymetric data include sonar measured data and scanning charts, and their accuracy is usually quite different. This makes the source of training sample points, the precision of data acquisition equipment and acquisition process, and the spatial distribution of sample points all worthy of further study.
- (d)
- Deep learning is a data-driven model method. To ensure the learning effect of the deep model, abundant and diverse training data are required in the training process. However, in the water depth inversion work, the lack of sufficient samples is very common. “few shot learning” and “transfer learning” may provide solutions and research directions for this problem.
- (e)
- The water depth control points are the basis of building the model, and their quality is very important. In the real scene, the image pixels corresponding to the water depth points in the sea chart are affected by the surface flare and the boundary of the aquaculture area, resulting in the distortion of the pixel spectrum of the remote sensing image, and the predicted values of these pixels are greatly different from the measured values. In fact, these pixels have been “polluted” and are no longer suitable as control points. It should be pointed out that the GRU model also pays attention to the number of control points, and maintaining a certain number of control points is the premise of training an effective model. In this paper, a total of 596 control points was collected. For the points with more than one standard deviation, we carried out a visual interpretation to ensure that they were “polluted” pixels, and 16 points were deleted, and 97% of the points were retained. Therefore, on the premise of ensuring the quality of water depth control points, the quantity of control points is also guaranteed.
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ma, Y.; Zhang, J.; Zhang, J.Y.; Zhang, Z.; Wang, J.J. Progress in Shallow Water Depth Mapping from Optical Remote Sensing. Adv. Mar. Sci. 2018, 36, 5–25. [Google Scholar]
- Kutser, T.; Hedley, J.; Giardino, C.; Roelfsema, C.; Brando, V.E. Remote sensing of shallow waters—A 50 year retrospective and future directions. Remote Sens. Environ. 2020, 240, 111619. [Google Scholar] [CrossRef]
- Lyzenga, D.R. Passive remote sensing techniques for mapping water depth and bottom features. Appl. Opt. 1978, 17, 379–383. [Google Scholar] [CrossRef] [PubMed]
- Lyzenga, D.R.; Malinas, N.P.; Tanis, F.J. Multispectral bathymetry using a simple physically based algorithm. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2251–2259. [Google Scholar] [CrossRef]
- Figueiredo, I.N.; Pinto, L.; Gonçalves, G.A. Modified Lyzenga’s model for multispectral bathymetry using Tikhonov regularization. IEEE Geosci. Remote Sens. Lett. 2015, 13, 53–57. [Google Scholar] [CrossRef]
- Chen, Q.; Deng, R.; Qin, Y.; He, Y.; Wang, W. Water depth extraction from remote sensing image in Feilaixia reservoir. Acta Sci. Nat. Univ. Sunyatseni 2012, 1, 122–127. [Google Scholar]
- Polcyn, F.C.; Sattinger, I.J. Water depth determinations using remote sensing techniques. Remote Sens. Environ. 1969, VI, 1017. [Google Scholar]
- Paredes, J.M.; Spero, R.E. Water depth mapping from passive remote sensing data under a generalized ratio assumption. Appl. Opt. 1983, 22, 1134–1135. [Google Scholar] [CrossRef]
- Stumpf, R.P.; Holderied, K.; Sinclair, M. Determination of water depth with high-resolution satellite imagery over variable bottom types. Limnol. Oceanogr. 2003, 48, 547–556. [Google Scholar] [CrossRef]
- Zhang, D.; Zhang, Y.; Wang, W. Establishment of a RS-Fathoming Correlation Model. J. Hohai Univ. 1998, 26, 95–99. [Google Scholar]
- Zhang, Y.; Zhang, Y.; Zhang, D. An underwater bathymetry reversion in the radial sand ridge group region of the southern Huanghai Sea using the remote sensing technology. Acta Oceanol. Sin. 2009, 31, 39–45. [Google Scholar]
- Xiaodong, Z.; Shouxian, Z.; Wenhua, Z.; Wenjing, Z. The Analysis of ETM Image’s Spectral and Its Implication on Water Depth Inversion iniamen Bay. In Proceedings of the International Conference on Remote Sensing, Environment and Transportation Engineering (RSETE 2013), Nanjing, China, 26–28 July 2013. [Google Scholar]
- Li, L.I. Remote sensing bathymetric inversion for the Xisha Islands based on WorldView-2 data: A case study of Zhaoshu Island and South Island. Remote Sens. Land Resour. 2016, 28, 170–175. [Google Scholar]
- Kerr, J.M.; Purkis, S. An algorithm for optically-deriving water depth from multispectral imagery in coral reef landscapes in the absence of ground-truth data. Remote Sens. Environ. 2018, 210, 307–324. [Google Scholar] [CrossRef]
- Goodman, J.A.; Lay, M.; Ramirez, L.; Ustin, S.L.; Haverkamp, P.J. Confidence Levels, Sensitivity, and the Role of Bathymetry in Coral Reef Remote Sensing. Remote Sens. 2020, 12, 496. [Google Scholar] [CrossRef] [Green Version]
- Guo, K.; Xu, W.; Liu, Y.; He, X.; Tian, Z. Gaussian half-wavelength progressive decomposition method for waveform processing of airborne laser bathymetry. Remote Sens. 2018, 10, 35. [Google Scholar] [CrossRef] [Green Version]
- Schwarz, R.; Mandlburger, G.; Pfennigbauer, M.; Pfeifer, N. Design and evaluation of a full-wave surface and bottom-detection algorithm for LiDAR bathymetry of very shallow waters. ISPRS J. Photogramm. Remote Sens. 2019, 150, 1–10. [Google Scholar] [CrossRef]
- Yang, A.; Wu, Z.; Yang, F.; Su, D.; Ma, Y.; Zhao, D.; Qi, C. Filtering of airborne LiDAR bathymetry based on bidirectional cloth simulation. ISPRS J. Photogramm. Remote Sens. 2020, 163, 49–61. [Google Scholar] [CrossRef]
- Manessa, M.D.M.; Kanno, A.; Sekine, M.; Haidar, M.; Yamamoto, K.; Imai, T.; Higuchi, T. Satellite-derived bathymetry using random forest algorithm and worldview-2 Imagery. Geoplan. J. Geomat. Plan 2016, 3, 117–126. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Liu, H.; Su, H.; Wang, J. Bathymetry retrieval from optical images with spatially distributed support vector machines. GISci. Remote Sens. 2019, 56, 323–337. [Google Scholar] [CrossRef]
- Fan, Y.G.; Liu, J.X. Water depth remote sensing retrieval model based on artificial neural network techniques. Hydrogr. Surv. Charting 2015, 35, 20–23. [Google Scholar]
- Wang, Y.; Zhou, X.; Li, C.; Chen, Y.; Yang, L. Bathymetry Model Based on Spectral and Spatial Multifeatures of Remote Sensing Image. IEEE Geosci. Remote Sens. Lett. 2019, 17, 37–41. [Google Scholar] [CrossRef]
- Ai, B.; Wen, Z.; Wang, Z.; Wang, R.; Su, D.; Li, C.; Yang, F. Convolutional neural network to retrieve water depth in marine shallow water area from remote sensing images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 2888–2898. [Google Scholar] [CrossRef]
- Liu, Y.; Deng, R.; Li, J.; Qin, Y.; Xiong, L.; Chen, Q.; Liu, X. Multispectral bathymetry via linear unmixing of the benthic reflectance. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens 2018, 11, 4349–4363. [Google Scholar] [CrossRef]
- Zeisse, C.R. Radiance of the Ocean Horizon. J. Opt. Soc. Am. 1995, 12, 2022–2030. [Google Scholar] [CrossRef]
- Li, J.; Knapp, D.E.; Schill, S.R.; Roelfsema, C.; Phinn, S.; Silman, M.; Mascaro, J.; Asner, G.P. Adaptive bathymetry estimation for shallow coastal waters using Planet Dove satellites. Remote Sens. Environ. 2019, 232, 111302. [Google Scholar] [CrossRef]
- Asner, G.P.; Vaughn, N.R.; Balzotti, C.; Brodrick, P.G.; Heckler, J. High-Resolution Reef Bathymetry and Coral Habitat Complexity from Airborne Imaging Spectroscopy. Remote Sens. 2020, 12, 310. [Google Scholar] [CrossRef] [Green Version]
- Agrafiotis, P.; Karantzalos, K.; Georgopoulos, A.; Skarlatos, D. Correcting image refraction: Towards accurate aerial image-based bathymetry mapping in shallow waters. Remote Sens. 2020, 12, 322. [Google Scholar] [CrossRef] [Green Version]
- Mobley, C.D. Light and Water: Radiative Transfer in Natural Waters; Academic Press: New York, NY, USA, 1994. [Google Scholar]
- Alpers, W. Theory of radar imaging of internal waves. Nature 1985, 314, 245–247. [Google Scholar] [CrossRef]
- Cox, C.; Munk, W. Measurement of the Roughness of the Sea Surface from Photographs of the Sun’s Glitte. J. Opt. Soc. Am. 1954, 44, 838–850. [Google Scholar] [CrossRef]
- Zhang, H.G.; Yang, K.; Lou, X.L.; Li, D.L.; Shi, A.Q.; Fu, B. Bathymetric Mapping of Submarine Sand Waves Using Multi-angle Sun Glitter Imagery: A Case of the Taiwan Banks with ASTER Stereo Imagery. J. Appl. Remote Sens. 2015, 9, 095988. [Google Scholar] [CrossRef] [Green Version]
- Cho, K.; Van Merriënboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning phrase representations using RNN encoder-decoder for statistical machine translation. arXiv 2014, arXiv:1406.1078. [Google Scholar]
- Irie, K.; Tüske, Z.; Alkhouli, T.; Schlüter, R.; Ney, H. LSTM, GRU, Highway and a Bit of Attention: An Empirical Overview for Language Modeling in Speech Recognition. In Proceedings of the Interspeech (International Speech Communication Association), San Francisco, CA, USA, 8–12 September 2016; pp. 3519–3523. [Google Scholar]
- Athiwaratkun, B.; Stokes, J.W. Malware classification with LSTM and GRU language models and a character-level CNN. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, New Orleans, LA, USA, 5–9 March 2017; pp. 2482–2486. [Google Scholar]
- Zhang, Y.; Lu, W.; Ou, W.; Zhang, G.; Zhang, X.; Cheng, J.; Zhang, W. Chinese medical question answer selection via hybrid models based on CNN and GRU. Multimed. Tools Appl. 2019, 2019, 1–26. [Google Scholar] [CrossRef]
- Jensen, J.R. Introductory Digital Image Processing: A Remote Sensing Perspective, 2nd ed.; Prentice-Hall Inc.: Upper Saddle River, NJ, USA, 1996. [Google Scholar]
- Research System Inc. FLAASH User’s Guide; ENVI FLAASH Version 1.0; Research System Inc.: Boulder, CO, USA, 2001. [Google Scholar]
- Munson, B.R.; Okiishi, T.H.; Huebsch, W.W.; Rothmayer, A.P. Fluid Mechanics; Wiley: Singapore, 2013. [Google Scholar]
- Bengio, Y.; Courville, A.; Vincent, P. Representation learning: A review and new perspectives. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1798–1828. [Google Scholar] [CrossRef] [PubMed]














| Parameters | Value |
|---|---|
| Spectral region | Band 1:450–520 nm |
| Band 2:520–590 nm | |
| Band 3:630–690 nm | |
| Band 4:770–890 nm | |
| Spatial resolution | 16 m |
| Swath | 800 km |
| Solar azimuth | 159.4° |
| Solar zenith | 56.1° |
| Satellite azimuth | 101.4° |
| Satellite zenith | 63.3° |
| Model | R2 | RMSE (m) | MAE (m) | MRE (%) |
|---|---|---|---|---|
| Log linear | 0.60 | 6.90 | 5.20 | 50.4 |
| Stumpf | 0.16 | 10.20 | 8.10 | 91.6 |
| MLP | 0.69 | 6.30 | 4.80 | 30.4 |
| GRU | 0.88 | 3.69 | 2.72 | 19.6 |
| Structure | R2 | RMSE (m) | MAE (m) | MRE (%) | Time (s) |
|---|---|---|---|---|---|
| 50 | 0.83 | 4.53 | 3.20 | 20.71 | 191 |
| 100 | 0.82 | 4.62 | 3.20 | 20.52 | 200 |
| 200 | 0.80 | 4.84 | 3.40 | 21.73 | 217 |
| 400 | 0.81 | 4.74 | 3.40 | 20.90 | 298 |
| 25–50 | 0.85 | 4.24 | 3.01 | 19.08 | 322 |
| 50–100 | 0.92 | 3.13 | 2.26 | 14.96 | 316 |
| 100–200 | 0.92 | 3.13 | 2.25 | 15.01 | 345 |
| 200–400 | 0.91 | 3.26 | 2.29 | 14.78 | 515 |
| 400–800 | 0.91 | 3.34 | 2.39 | 14.85 | 1059 |
| 25–50–25 | 0.83 | 4.47 | 3.11 | 18.55 | 482 |
| 50–100–50 | 0.84 | 4.41 | 2.96 | 17.75 | 446 |
| 100–200–100 | 0.90 | 3.38 | 2.38 | 15.56 | 467 |
| 200–400–200 | 0.91 | 3.24 | 2.28 | 14.98 | 680 |
| Optimizer | R2 | RMSE (m) | MAE (m) | MRE (%) |
|---|---|---|---|---|
| SGD | 0.85 | 4.26 | 3 | 22.06 |
| RMSprop | 0.91 | 3.21 | 2.32 | 16.89 |
| Adagrad | 0.8 | 4.89 | 3.47 | 23.69 |
| Adadelta | 0.91 | 3.21 | 2.22 | 15.72 |
| Adam | 0.92 | 3.13 | 2.19 | 15.39 |
| Adamax | 0.91 | 3.18 | 2.27 | 16.35 |
| Batch Size | R2 | RMSE (m) | MAE (m) | MRE (%) | Time (s) |
|---|---|---|---|---|---|
| 8 | 0.91 | 3.3 | 2.38 | 15.86 | 1468 |
| 16 | 0.91 | 3.25 | 2.34 | 15.27 | 727 |
| 32 | 0.91 | 3.28 | 2.39 | 15.74 | 393 |
| 64 | 0.91 | 3.21 | 2.31 | 15.11 | 202 |
| 128 | 0.89 | 3.54 | 2.62 | 17.14 | 108 |
| 256 | 0.88 | 3.72 | 2.76 | 18.73 | 70 |
| Control Point | R2 | RMSE (m) | MAE (m) | MRE (%) | Time (s) |
|---|---|---|---|---|---|
| 10% | 0.82 | 4.75 | 3.35 | 27.04 | 103 |
| 20% | 0.85 | 4.37 | 3.20 | 24.11 | 149 |
| 40% | 0.89 | 3.78 | 2.78 | 20.33 | 219 |
| 60% | 0.90 | 3.49 | 2.50 | 19.55 | 391 |
| 80% | 0.92 | 3.24 | 2.33 | 18.20 | 508 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Leng, Z.; Zhang, J.; Ma, Y.; Zhang, J. Underwater Topography Inversion in Liaodong Shoal Based on GRU Deep Learning Model. Remote Sens. 2020, 12, 4068. https://doi.org/10.3390/rs12244068
Leng Z, Zhang J, Ma Y, Zhang J. Underwater Topography Inversion in Liaodong Shoal Based on GRU Deep Learning Model. Remote Sensing. 2020; 12(24):4068. https://doi.org/10.3390/rs12244068
Chicago/Turabian StyleLeng, Zihao, Jie Zhang, Yi Ma, and Jingyu Zhang. 2020. "Underwater Topography Inversion in Liaodong Shoal Based on GRU Deep Learning Model" Remote Sensing 12, no. 24: 4068. https://doi.org/10.3390/rs12244068
APA StyleLeng, Z., Zhang, J., Ma, Y., & Zhang, J. (2020). Underwater Topography Inversion in Liaodong Shoal Based on GRU Deep Learning Model. Remote Sensing, 12(24), 4068. https://doi.org/10.3390/rs12244068