Scattering Feature Set Optimization and Polarimetric SAR Classification Using Object-Oriented RF-SFS Algorithm in Coastal Wetlands
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area and Data
2.2. Polarimetric Scattering Features Extraction
2.2.1. Matrix Element Features
2.2.2. Polarimetric Decomposition Features
2.3. Object-Oriented Method
2.4. Random Forest and Feature Set Optimization
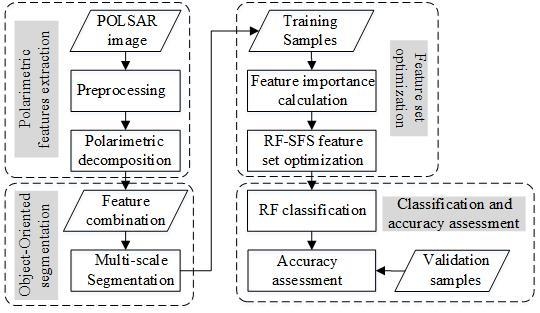
2.5. Experimental Flowchart
- (1)
- Filtering and other preprocessing were applied to the original polarimetric SAR data;
- (2)
- Twenty polarimetric decompositions listed in Table 2 were utilized to decompose the filtered coherent matrix, and 93 polarimetric decomposition features were obtained. Three scattering matrix elements, S11, S12 and S22, were used as matrix features, and thus a total of 96 polarimetric scattering features could be obtained;
- (3)
- The scattering features obtained from the previous step were combined into a multi-band image, to which object-oriented multi-scale segmentation was then performed;
- (4)
- Training samples based on the segmented object as the basic unit were randomly selected;
- (5)
- Formula (7) was used to calculate the importance of all polarimetric scattering features of training samples;
- (6)
- The features were ranked according to the importance value;
- (7)
- Using the sequential forward selection algorithm to optimize the feature set, the feature subset with the least number of features and the highest classification accuracy was obtained;
- (8)
- The selected optimal polarimetric feature subset was classified based on the object-oriented random forest model;
- (9)
- The classification accuracy was calculated by using validation samples.
3. Results and Discussion
3.1. Importance Analysis of Polarimetric Features and Feature Set Optimization
3.2. Classification Results
3.3. Discussion
4. Conclusions
- (1)
- The proposed method calculated the importance of each polarimetric feature in the construction of a random forest model, and the sequence forward selection algorithm was applied to select the optimal polarimetric feature set that is suitable for Jiangsu coastal wetlands classification according to the importance value. This method provided a quantitative reference for the reasonable optimization of feature sets;
- (2)
- The importance values of features from the scattering matrix and the four decomposition algorithms, namely, decomposition, Yamaguchi3 decomposition, VanZyl3 decomposition, and Krogager decomposition, were higher than other features. This indicated that these features were more important and were determined to be very supportive of land cover identification in the Jiangsu coastal wetlands;
- (3)
- Compared with the object-oriented QUEST decision tree algorithm, regardless of whether the latter has been pruned, the proposed object-oriented RF-SFS method can achieve higher classification accuracies without artificial pruning.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Michener, W.K.; Blood, E.R.; Bildstein, K.L.; Brinson, M.M.; Gardner, L.R. Climate change, hurricanes and tropical storms, and rising sea level in coastal wetlands. Ecol. Appl. 1997, 7, 770–801. [Google Scholar] [CrossRef]
- Costanza, R.; Pérez-Maqueo, O.; Martinez, M.L.; Sutton, P.; Anderson, S.J.; Mulder, K. The value of coastal wetlands for hurricane protection. Ambio 2008, 37, 241–249. [Google Scholar] [CrossRef]
- Perillo, G.; Wolanski, E.; Cahoon, D.R.; Hopkinson, C.S. Coastal Wetlands: An Integrated Ecosystem Approach; Elsevier: Amsterdam, The Netherlands, 2018. [Google Scholar]
- Prince, H.H. Coastal Wetlands; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Sievers, M.; Brown, C.J.; Tulloch, V.J.; Pearson, R.M.; Haig, J.A.; Turschwell, M.P.; Connolly, R.M. The role of vegetated coastal wetlands for marine megafauna conservation. Trends Ecol. Evol. 2019, 34, 807–817. [Google Scholar] [CrossRef] [PubMed]
- Hardisky, M.; Gross, M.; Klemas, V. Remote sensing of coastal wetlands. Bioscience 1986, 36, 453–460. [Google Scholar] [CrossRef]
- Klemas, V. Remote sensing of wetlands: Case studies comparing practical techniques. J. Coast. Res. 2011, 27, 418–427. [Google Scholar]
- Doughty, C.L.; Cavanaugh, K.C. Mapping Coastal Wetland Biomass from High Resolution Unmanned Aerial Vehicle (UAV) Imagery. Remote Sens. 2019, 11, 540. [Google Scholar] [CrossRef] [Green Version]
- Verstraete, M.M.; Pinty, B.; Myneni, R.B. Potential and limitations of information extraction on the terrestrial biosphere from satellite remote sensing. Remote Sens. Environ. 1996, 58, 201–214. [Google Scholar] [CrossRef]
- Adam, E.; Mutanga, O.; Rugege, D. Multispectral and hyperspectral remote sensing for identification and mapping of wetland vegetation: A review. Wetl. Ecol. Manag. 2010, 18, 281–296. [Google Scholar] [CrossRef]
- Kasischke, E.S.; Bourgeau-Chavez, L.L. Monitoring South Florida wetlands using ERS-1 SAR imagery. Photogramm. Eng. Remote Sens. 1997, 63, 281–291. [Google Scholar]
- White, L.; Brisco, B.; Dabboor, M.; Schmitt, A.; Pratt, A. A collection of SAR methodologies for monitoring wetlands. Remote Sens. 2015, 7, 7615–7645. [Google Scholar] [CrossRef] [Green Version]
- Mohammadimanesh, F.; Salehi, B.; Mahdianpari, M.; Brisco, B.; Motagh, M. Multi-temporal, multi-frequency, and multi-polarization coherence and SAR backscatter analysis of wetlands. ISPRS-J. Photogramm. Remote Sens. 2018, 142, 78–93. [Google Scholar] [CrossRef]
- Amani, M.; Salehi, B.; Mahdavi, S.; Brisco, B. Separability analysis of wetlands in Canada using multi-source SAR data. GISci. Remote Sens. 2019, 56, 1233–1260. [Google Scholar] [CrossRef]
- Choe, B.-H.; Kim, D.-j.; Hwang, J.-H.; Oh, Y.; Moon, W.M. Detection of oyster habitat in tidal flats using multi-frequency polarimetric SAR data. Estuar. Coast. Shelf Sci. 2012, 97, 28–37. [Google Scholar] [CrossRef]
- Chauhan, S.; Srivastava, H.S. Comparative evaluation of the sensitivity of multi-polarized SAR and optical data for various land cover classes. Int. J. Adv. Remote Sens. GIS Geogr 2016, 4, 1–14. [Google Scholar]
- Pereira, L.; Furtado, L.; Novo, E.; Sant’Anna, S.; Liesenberg, V.; Silva, T. Multifrequency and Full-Polarimetric SAR Assessment for Estimating Above Ground Biomass and Leaf Area Index in the Amazon Várzea Wetlands. Remote Sens. 2018, 10, 1355. [Google Scholar] [CrossRef] [Green Version]
- Millard, K.; Richardson, M. Wetland mapping with LiDAR derivatives, SAR polarimetric decompositions, and LiDAR–SAR fusion using a random forest classifier. Can. J. Remote Sens. 2013, 39, 290–307. [Google Scholar] [CrossRef]
- de Almeida Furtado, L.F.; Silva, T.S.F.; de Moraes Novo, E.M.L. Dual-season and full-polarimetric C band SAR assessment for vegetation mapping in the Amazon várzea wetlands. Remote Sens. Environ. 2016, 174, 212–222. [Google Scholar] [CrossRef] [Green Version]
- Hong, S.-H.; Kim, H.-O.; Wdowinski, S.; Feliciano, E. Evaluation of polarimetric SAR decomposition for classifying wetland vegetation types. Remote Sens. 2015, 7, 8563–8585. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; He, X.; Wang, J. Classification of coastal wetlands in eastern China using polarimetric SAR data. Arab. J. Geosci. 2015, 8, 10203–10211. [Google Scholar] [CrossRef]
- Touzi, R.; Deschamps, A.; Rother, G. Wetland characterization using polarimetric RADARSAT-2 capability. Can. J. Remote Sens. 2007, 33, S56–S67. [Google Scholar] [CrossRef]
- Chen, Y.; He, X.; Wang, J.; Xiao, R. The influence of polarimetric parameters and an object-based approach on land cover classification in coastal wetlands. Remote Sens. 2014, 6, 12575–12592. [Google Scholar] [CrossRef] [Green Version]
- Niu, X.; Ban, Y. Multi-temporal RADARSAT-2 polarimetric SAR data for urban land-cover classification using an object-based support vector machine and a rule-based approach. Int. J. Remote Sens. 2013, 34, 1–26. [Google Scholar] [CrossRef]
- Blaschke, T. Object based image analysis for remote sensing. ISPRS-J. Photogramm. Remote Sens. 2010, 65, 2–16. [Google Scholar] [CrossRef] [Green Version]
- Blaschke, T.; Lang, S.; Hay, G. Object-Based Image Analysis: Spatial Concepts for Knowledge-Driven Remote Sensing Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Ma, L.; Li, M.; Ma, X.; Cheng, L.; Du, P.; Liu, Y. A review of supervised object-based land-cover image classification. ISPRS-J. Photogramm. Remote Sens. 2017, 130, 277–293. [Google Scholar] [CrossRef]
- Ban, Y.; Hu, H.; Rangel, I.M. Fusion of Quickbird MS and RADARSAT SAR data for urban land-cover mapping: Object-based and knowledge-based approach. Int. J. Remote Sens. 2010, 31, 1391–1410. [Google Scholar] [CrossRef]
- Fu, B.; Wang, Y.; Campbell, A.; Li, Y.; Zhang, B.; Yin, S.; Xing, Z.; Jin, X. Comparison of object-based and pixel-based Random Forest algorithm for wetland vegetation mapping using high spatial resolution GF-1 and SAR data. Ecol. Indic. 2017, 73, 105–117. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Classification and regression by randomForest. R. News 2002, 2, 18–22. [Google Scholar]
- Pal, M. Random forest classifier for remote sensing classification. Int. J. Remote Sens. 2005, 26, 217–222. [Google Scholar] [CrossRef]
- Boonprong, S.; Cao, C.; Chen, W.; Bao, S. Random Forest Variable Importance Spectral Indices Scheme for Burnt Forest Recovery Monitoring—Multilevel RF-VIMP. Remote Sens. 2018, 10, 807. [Google Scholar] [CrossRef] [Green Version]
- Belgiu, M.; Drăguţ, L. Random forest in remote sensing: A review of applications and future directions. ISPRS-J. Photogramm. Remote Sens. 2016, 114, 24–31. [Google Scholar]
- Lebourgeois, V.; Dupuy, S.; Vintrou, É.; Ameline, M.; Butler, S.; Bégué, A. A combined random forest and OBIA classification scheme for mapping smallholder agriculture at different nomenclature levels using multisource data (simulated Sentinel-2 time series, VHRS and DEM). Remote Sens. 2017, 9, 259. [Google Scholar] [CrossRef] [Green Version]
- Lee, J.-S.; Pottier, E. Polarimetric Radar Imaging: From Basics to Applications; CRC press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Cloude, S.R.; Pottier, E. A review of target decomposition theorems in radar polarimetry. IEEE Trans. Geosci. Remote Sens. 1996, 34, 498–518. [Google Scholar] [CrossRef]
- Cloude, S.R.; Pottier, E. An entropy based classification scheme for land applications of polarimetric SAR. IEEE Trans. Geosci. Remote Sens. 1997, 35, 68–78. [Google Scholar] [CrossRef]
- Krogager, E. New decomposition of the radar target scattering matrix. Electron. Lett. 1990, 26, 1525–1527. [Google Scholar] [CrossRef]
- Huynen, J.R. Stokes matrix parameters and their interpretation in terms of physical target properties. In Proceedings of the Polarimetry: Radar, infrared, visible, ultraviolet, and X-ray, Nantes, France, 20–22 March 1990. [Google Scholar]
- Barnes, R. Roll-invariant decompositions for the polarization covariance matrix. In Proceedings of the Polarimetry Technology Workshop, Redstone Arsenal, AL, USA, 16–18 August 1988. [Google Scholar]
- Holm, W.A.; Barnes, R.M. On radar polarization mixed target state decomposition techniques. In Proceedings of the 1988 IEEE National Radar Conference, Ann Arbor, MI, USA, 20–21 April 1988; pp. 249–254. [Google Scholar]
- van Zyl, J.J. Application of Cloude’s target decomposition theorem to polarimetric imaging radar data. Radar Polarim. 1993, 1748, 184–191. [Google Scholar]
- Pottier, E.; Lee, J.-S. Application of the «H/A/alpha» polarimetric decomposition theorem for unsupervised classification of fully polarimetric SAR data based on the wishart distribution. In Proceedings of the SAR workshop: CEOS Committee on Earth Observation Satellites, Toulouse, France, 26–29 October 1999; pp. 335–340. [Google Scholar]
- Freeman, A. Fitting a two-component scattering model to polarimetric SAR data from forests. IEEE Trans. Geosci. Remote Sens. 2007, 45, 2583–2592. [Google Scholar] [CrossRef]
- Freeman, A.; Durden, S.L. A three-component scattering model for polarimetric SAR data. IEEE Trans. Geosci. Remote Sens. 1998, 36, 963–973. [Google Scholar] [CrossRef] [Green Version]
- Yamaguchi, Y.; Singh, G.; Yi, C.; Park, S.E.; Yamada, H.; Sato, R. Comparison of model-based four-component scattering power decompositions. In Proceedings of the 2013 Asia-Pacific Conference on Synthetic Aperture Radar (APSAR), Tsukuba, Japan, 23–27 September 2013; pp. 92–95. [Google Scholar]
- Yamaguchi, Y.; Moriyama, T.; Ishido, M.; Yamada, H. Four-component scattering model for polarimetric SAR image decomposition. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1699–1706. [Google Scholar] [CrossRef]
- Neumann, M.; Ferro-Famil, L.; Pottier, E. A general model-based polarimetric decomposition scheme for vegetated areas. In Proceedings of the 4th International Workshop on Science and Applications of SAR Polarimetry and Polarimetric Interferometry-PolInSAR, Frascati, Italy, 26–30 January 2009. [Google Scholar]
- Touzi, R. Target scattering decomposition in terms of roll-invariant target parameters. IEEE Trans. Geosci. Remote Sens. 2006, 45, 73–84. [Google Scholar] [CrossRef]
- An, W.; Cui, Y.; Yang, J. Three-component model-based decomposition for polarimetric SAR data. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2732–2739. [Google Scholar]
- An, W.; Xie, C.; Yuan, X.; Cui, Y.; Yang, J. Four-component decomposition of polarimetric SAR images with deorientation. IEEE Geosci. Remote Sens. Lett. 2011, 8, 1090–1094. [Google Scholar] [CrossRef]
- Arii, M.; van Zyl, J.J.; Kim, Y. Adaptive model-based decomposition of polarimetric SAR covariance matrices. IEEE Trans. Geosci. Remote Sens. 2010, 49, 1104–1113. [Google Scholar] [CrossRef]
- Arii, M.; van Zyl, J.; Kim, Y. Improvement of adaptive-model based decomposition with polarization orientation compensation. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Munich, Germany, 22–27 July 2012; pp. 95–98. [Google Scholar]
- Qi, Z.; Yeh, A.G.-O.; Li, X.; Lin, Z. A novel algorithm for land use and land cover classification using RADARSAT-2 polarimetric SAR data. Remote Sens. Environ. 2012, 118, 21–39. [Google Scholar] [CrossRef]
- Addink, E.A.; De Jong, S.M.; Pebesma, E.J. The importance of scale in object-based mapping of vegetation parameters with hyperspectral imagery. Photogramm. Eng. Remote Sens. 2007, 73, 905–912. [Google Scholar] [CrossRef]
- Anders, N.S.; Seijmonsbergen, A.C.; Bouten, W. Segmentation optimization and stratified object-based analysis for semi-automated geomorphological mapping. Remote Sens. Environ. 2011, 115, 2976–2985. [Google Scholar] [CrossRef]
- Kavzoglu, T.; Yildiz, M. Parameter-based performance analysis of object-based image analysis using aerial and Quikbird-2 images. In Proceedings of the ISPRS Annals of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Istanbul, Turkey, 29 September–2 October 2014; pp. 31–37. [Google Scholar]
- Mitchell, M.W. Bias of the Random Forest out-of-bag (OOB) error for certain input parameters. Open J. Statist. 2011, 1, 205. [Google Scholar] [CrossRef] [Green Version]
- Millard, K.; Richardson, M. On the importance of training data sample selection in random forest image classification: A case study in peatland ecosystem mapping. Remote Sens. 2015, 7, 8489–8515. [Google Scholar] [CrossRef] [Green Version]
- Mani, K.; Kalpana, P. An efficient feature selection based on bayes theorem, self information and sequential forward selection. Int. J. Inform. Eng. Electron. Bus. 2016, 8, 46. [Google Scholar] [CrossRef] [Green Version]
- Ghatkar, J.G.; Singh, R.K.; Shanmugam, P. Classification of algal bloom species from remote sensing data using an extreme gradient boosted decision tree model. Int. J. Remote Sens. 2019, 40, 9412–9438. [Google Scholar] [CrossRef]







| Class | Training Samples | Validation Samples | Total |
|---|---|---|---|
| Fish pond | 5383 | 3027 | 8410 |
| Irrigable land | 1909 | 1024 | 2933 |
| Reed and Alterniflora | 4654 | 3021 | 7675 |
| Suaeda salsa | 2658 | 1486 | 4144 |
| Rice paddy | 2542 | 1324 | 3866 |
| River | 1599 | 876 | 2475 |
| Road | 1049 | 654 | 1703 |
| Sand | 1996 | 1022 | 3018 |
| Sea | 6864 | 3873 | 10,737 |
| Total | 28,654 | 16,307 | 44,961 |
| Decompositions 1 | Polarimetric Decomposition Parameters | ||
|---|---|---|---|
| Pauli | Pauli_a | Pauli_b | Pauli_c |
| Krogager | Krogager_Ks | Krogager_Kd | Krogager_Kh |
| Huynen | Huynen_T11 | Huynen_T22 | Huynen_T33 |
| Barnes1 | Barnes1_T11 | Barnes1_T22 | Barnes1_T33 |
| Barnes2 | Barnes2_T11 | Barnes2_T22 | Barnes2_T33 |
| Holm1 | Holm1_T11 | Holm1_T22 | Holm1_T33 |
| Holm2 | Holm2_T11 | Holm2_T22 | Holm2_T33 |
| VanZyl3 | VanZyl3_Vol | VanZyl3_Odd | VanZyl3_Dbl |
| Cloude | Cloude_T11 | Cloude_T22 | Cloude_T33 |
| H/A/Alpha | H/A/A_T11 | H/A/A_T22 | H/A/A_T33 |
| Entropy | Anisotropy | Shannon Entropy | |
| DERD | Polarization Asymmetry | Polarization Fraction | |
| SERD | Radar Vegetation Index | Anisotropy12 | |
| Pedestal Height | Alpha (,α1,α2,α3) | Anisotropy_Lueneburg | |
| Pseudo Probabilities (p1, p2, p3) Lambda | |||
| Freeman2 | Freeman2_Vol | Freeman2_Ground | |
| Freeman3 | Freeman_Vol | Freeman_Odd | Freeman_Dbl |
| Yamaguchi3 | Yamaguchi3_Vol | Yamaguchi3_Odd | Yamaguchi3_Dbl |
| Yamaguchi4 | Yamaguchi4_Vol | Yamaguchi4_Odd | Yamaguchi4_Dbl |
| Yamaguchi4_Hlx | |||
| Neumann | Neumann_delta_mod | Neumann_delta_pha | Neumann_tau |
| Touzi | TSVM_alpha_s | TSVM_alpha_s1 | TSVM_alpha_s2 |
| TSVM_alpha_s3 | TSVM_tau_m | TSVM_tau_m1 | |
| TSVM_tau_m2 TSVM_phi_s2 TSVM_psi1 TSVM_psi | TSVM_tau_m3 TSVM_phi_s3 TSVM_psi2 | TSVM_phi_s1 TSVM_phi_s TSVM_psi3 | |
| An_Yang3 | An_Yang3_Vol | An_Yang3_Odd | An_Yang3_Dbl |
| An_Yang4 | An_Yang4_Vol | An_Yang4_Odd | An_Yang4_Dbl |
| An_Yang4_Hlx | |||
| Arii3_NNED | Arii3_NNED_Vol | Arii3_NNED_Odd | Arii3_NNED_Dbl |
| Arii3_ANNED | Arii3_ANNED_Vol | Arii3_ANNED_Odd | Arii3_ANNED_Odd |
| Polarimetric Feature | IM | Polarimetric Feature | IM | Polarimetric Feature | IM | |||
|---|---|---|---|---|---|---|---|---|
| 1 | S22 | 3.65 | 33 | Holm2_T11 | 1.37 | 65 | TSVM_psi | 0.66 |
| 2 | Barnes2_T22 | 2.87 | 34 | An_Yang4_Dbl | 1.34 | 66 | Alpha2 | 0.66 |
| 3 | Entropy_shannon | 2.68 | 35 | An_Yang4_Odd | 1.32 | 67 | Barnes1_T11 | 0.66 |
| 4 | S11 | 2.61 | 36 | Neumann_delta_pha | 1.26 | 68 | Pauli_T33 | 0.62 |
| 5 | Barnes1_T22 | 2.3 | 37 | Arii3_NNED_Dbl | 1.24 | 69 | Neumann_tau | 0.61 |
| 6 | Yamaguchi3_Dbl | 2.18 | 38 | Arii3_ANNED_Dbl | 1.24 | 70 | TSVM_phi_s2 | 0.59 |
| 7 | Entropy | 2.12 | 39 | TSVM_psi2 | 1.23 | 71 | Cloude_T22 | 0.59 |
| 8 | VanZyl3_Dbl | 2.01 | 40 | An_Yang3_Dbl | 1.22 | 72 | Barnes2_T11 | 0.58 |
| 9 | Arii3_NNED_Vol | 1.98 | 41 | Holm1_T11 | 1.22 | 73 | Holm2_T22 | 0.56 |
| 10 | Neumann_delta_mod | 1.98 | 42 | Anisotropy_Lueneburg | 1.21 | 74 | Huynen_T22 | 0.56 |
| 11 | Lambda | 1.96 | 43 | Anisotropy12 | 1.21 | 75 | TSVM_phi_s1 | 0.5 |
| 12 | VanZyl3_Vol | 1.96 | 44 | p2 | 1.18 | 76 | Holm1_T22 | 0.49 |
| 13 | HAA_T11 | 1.94 | 45 | Arii3_ANNED_Odd | 1.16 | 77 | TSVM_phi_s | 0.43 |
| 14 | Krogager_Kd | 1.88 | 46 | Yamaguchi4_Y40_Vol | 1.12 | 78 | TSVM_tau_m1 | 0.36 |
| 15 | S12 | 1.87 | 47 | Polarisation_Fraction | 1.12 | 79 | TSVM_tau_m | 0.36 |
| 16 | Krogager_Ks | 1.68 | 48 | RVI | 1.07 | 80 | TSVM_alpha_s2 | 0.36 |
| 17 | Yamaguchi3_Odd | 1.67 | 49 | Arii3_NNED_Odd | 1.05 | 81 | Alpha3 | 0.36 |
| 18 | An_Yang3_Vol | 1.66 | 50 | An_Yang3_Odd | 1.05 | 82 | Pauli_T11 | 0.36 |
| 19 | Pedestal | 1.66 | 51 | p3 | 1.05 | 83 | HAA_T33 | 0.35 |
| 20 | Freeman_Vol | 1.61 | 52 | Yamaguchi4_Y40_Odd | 1.02 | 84 | An_Yang4_Hlx | 0.33 |
| 21 | Alpha | 1.61 | 53 | Freeman2_Ground | 1.02 | 85 | TSVM_psi3 | 0.31 |
| 22 | Yamaguchi4_Y40_Dbl | 1.54 | 54 | Barnes2_T33 | 1.01 | 86 | TSVM_tau_m2 | 0.3 |
| 23 | Cloude_T11 | 1.54 | 55 | TSVM_alpha_s | 0.99 | 87 | Yamaguchi4_Y40_Hlx | 0.3 |
| 24 | p1 | 1.53 | 56 | HAA_T22 | 0.98 | 88 | Holm1_T33 | 0.3 |
| 25 | Yamaguchi3_Vol | 1.52 | 57 | Derd | 0.96 | 89 | Pauli_T22 | 0.3 |
| 26 | Freeman_Dbl | 1.51 | 58 | An_Yang4_Vol | 0.88 | 90 | Cloude_T33 | 0.27 |
| 27 | Huynen_T11 | 1.45 | 59 | Barnes1_T33 | 0.88 | 91 | Holm2_T33 | 0.25 |
| 28 | Freeman_Odd | 1.44 | 60 | Asymetry | 0.87 | 92 | Huynen_T33 | 0.23 |
| 29 | VanZyl3_Odd | 1.43 | 61 | Anisotropy | 0.85 | 93 | TSVM_alpha_s3 | 0.21 |
| 30 | Serd | 1.42 | 62 | Alpha1 | 0.75 | 94 | Krogager_Kh | 0.2 |
| 31 | Arii3_ANNED_Vol | 1.41 | 63 | TSVM_alpha_s1 | 0.68 | 95 | TSVM_tau_m3 | 0.17 |
| 32 | Freeman2_Vol | 1.38 | 64 | TSVM_psi1 | 0.66 | 96 | TSVM_phi_s3 | 0.12 |
| Class | FP | IL | RA | SS | RP | RI | RO | SA | S | Total | UA(%) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| FP | 2543 | 0 | 70 | 0 | 45 | 101 | 0 | 0 | 268 | 3027 | 84.01 |
| IL | 0 | 900 | 0 | 41 | 83 | 0 | 0 | 0 | 0 | 1024 | 87.89 |
| RA | 0 | 98 | 2534 | 182 | 120 | 0 | 0 | 87 | 0 | 3021 | 83.88 |
| SS | 0 | 0 | 138 | 1261 | 87 | 0 | 0 | 0 | 0 | 1486 | 84.86 |
| RP | 0 | 103 | 47 | 45 | 1129 | 0 | 0 | 0 | 0 | 1324 | 85.27 |
| RI | 99 | 0 | 0 | 0 | 0 | 734 | 0 | 0 | 43 | 876 | 83.79 |
| RO | 0 | 23 | 0 | 32 | 0 | 0 | 574 | 25 | 0 | 654 | 87.77 |
| SA | 0 | 35 | 30 | 0 | 0 | 0 | 54 | 903 | 0 | 1022 | 88.36 |
| S | 158 | 0 | 0 | 0 | 0 | 59 | 0 | 0 | 3656 | 3873 | 94.40 |
| Total | 2800 | 1159 | 2819 | 1561 | 1464 | 894 | 628 | 1015 | 3967 | 16307 | |
| PA(%) | 90.82 | 77.65 | 89.89 | 80.78 | 77.12 | 82.10 | 91.40 | 88.97 | 92.16 | ||
| OA(%) | 87.29 | Kappa coefficient | 0.8503 | ||||||||
| Class | FP | IR | RA | SS | RP | RI | RO | SA | S | Total | UA(%) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| FP | 2076 | 0 | 109 | 0 | 86 | 151 | 0 | 0 | 605 | 3027 | 68.58 |
| IR | 0 | 772 | 0 | 63 | 189 | 0 | 0 | 0 | 0 | 1024 | 75.39 |
| RA | 0 | 105 | 2204 | 226 | 403 | 0 | 0 | 83 | 0 | 3021 | 72.96 |
| SS | 0 | 119 | 198 | 912 | 257 | 0 | 0 | 0 | 0 | 1486 | 61.37 |
| PR | 0 | 255 | 58 | 50 | 961 | 0 | 0 | 0 | 0 | 1324 | 72.58 |
| RI | 299 | 0 | 0 | 0 | 0 | 494 | 0 | 0 | 83 | 876 | 56.39 |
| RO | 0 | 49 | 0 | 0 | 0 | 0 | 516 | 89 | 0 | 654 | 78.90 |
| SA | 0 | 53 | 61 | 0 | 0 | 0 | 62 | 846 | 0 | 1022 | 82.78 |
| S | 223 | 0 | 0 | 0 | 0 | 138 | 0 | 0 | 3512 | 3873 | 90.68 |
| Total | 2598 | 1353 | 2630 | 1251 | 1896 | 783 | 578 | 1018 | 4200 | 16307 | |
| PA(%) | 79.91 | 57.06 | 83.80 | 72.90 | 50.69 | 63.09 | 89.27 | 83.10 | 83.62 | ||
| OA(%) | 75.38 | Kappa coefficient | 0.7103 | ||||||||
| Class | FP | IR | RA | SS | RP | RI | RO | SA | S | Total | UA(%) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| FP | 2413 | 0 | 88 | 0 | 50 | 146 | 0 | 0 | 330 | 3027 | 79.72 |
| IR | 0 | 809 | 0 | 65 | 150 | 0 | 0 | 0 | 0 | 1024 | 79.00 |
| RA | 0 | 96 | 2490 | 239 | 111 | 0 | 0 | 85 | 0 | 3021 | 82.42 |
| SS | 0 | 105 | 129 | 1199 | 53 | 0 | 0 | 0 | 0 | 1486 | 80.69 |
| RP | 0 | 110 | 46 | 51 | 1117 | 0 | 0 | 0 | 0 | 1324 | 84.37 |
| RI | 132 | 0 | 0 | 0 | 0 | 684 | 0 | 0 | 60 | 876 | 78.08 |
| RO | 0 | 43 | 0 | 0 | 0 | 0 | 534 | 77 | 0 | 654 | 81.65 |
| SA | 0 | 42 | 35 | 0 | 0 | 0 | 32 | 913 | 0 | 1022 | 89.33 |
| S | 219 | 0 | 0 | 0 | 0 | 109 | 0 | 0 | 3545 | 3873 | 91.53 |
| Total | 2764 | 1205 | 2788 | 1554 | 1481 | 939 | 566 | 1075 | 3935 | 16307 | |
| PA(%) | 87.30 | 67.14 | 89.31 | 77.16 | 75.42 | 72.84 | 94.35 | 84.93 | 90.09 | ||
| OA(%) | 84.04 | Kappa coefficient | 0.8123 | ||||||||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; He, X.; Xu, J.; Zhang, R.; Lu, Y. Scattering Feature Set Optimization and Polarimetric SAR Classification Using Object-Oriented RF-SFS Algorithm in Coastal Wetlands. Remote Sens. 2020, 12, 407. https://doi.org/10.3390/rs12030407
Chen Y, He X, Xu J, Zhang R, Lu Y. Scattering Feature Set Optimization and Polarimetric SAR Classification Using Object-Oriented RF-SFS Algorithm in Coastal Wetlands. Remote Sensing. 2020; 12(3):407. https://doi.org/10.3390/rs12030407
Chicago/Turabian StyleChen, Yuanyuan, Xiufeng He, Jia Xu, Rongchun Zhang, and Yanyan Lu. 2020. "Scattering Feature Set Optimization and Polarimetric SAR Classification Using Object-Oriented RF-SFS Algorithm in Coastal Wetlands" Remote Sensing 12, no. 3: 407. https://doi.org/10.3390/rs12030407
APA StyleChen, Y., He, X., Xu, J., Zhang, R., & Lu, Y. (2020). Scattering Feature Set Optimization and Polarimetric SAR Classification Using Object-Oriented RF-SFS Algorithm in Coastal Wetlands. Remote Sensing, 12(3), 407. https://doi.org/10.3390/rs12030407