Discrimination of Biological Scatterers in Polarimetric Weather Radar Data: Opportunities and Challenges
Abstract
:1. Introduction
2. Materials and Methods
2.1. Sources of Identified Scatterer Type
2.2. Base Training and Test Dataset
2.3. Development of Classification Models
3. Results
3.1. Backscatter Values from Seven Types of Scatterer
3.1.1. Reflectivity Factor
3.1.2. Radial Velocity
3.1.3. Spectrum Width
3.1.4. Differential Reflectivity
3.1.5. Correlation Coefficient
3.1.6. Differential Phase
3.2. Aggregation and Phenotype
3.3. Radar Product Combinations
3.4. Natural History, Data Retention, and Mixed Scatterers
4. Discussion
4.1. Previous Studies
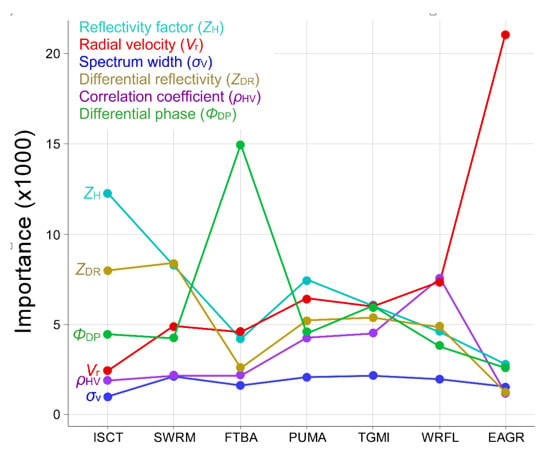
4.2. Aggregation, Variable Importance, and Phenotype
4.3. Natural History
4.4. Data Retention
4.5. Methodological Considerations
4.5.1. Training Data and Validation
4.5.2. Errors in Assignment and Classification
4.5.3. Mixed Scatterers
4.5.4. Radar Variable Combinations
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Supporting Tables
| Type | Reflectivity | Radial Velocity | Spectrum Width | Differential Reflectivity | Correlation Coefficient | Differential Phase | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Med | 25% | 75% | Med | 25% | 75% | Med | 25% | 75% | Med | 25% | 75% | Med | 25% | 75% | Med | 25% | 75% | |
| SWRM | 23.5 | 18.0 | 28.0 | −5.0 | −7.5 | −0.5 | 1.5 | 1.0 | 2.5 | 5.9 | 4.4 | 7.4 | 0.9 | 0.7 | 1.0 | 69.8 | 58.2 | 91.7 |
| ISCT | 2.0 | −1.5 | 6.0 | 1.0 | −4.0 | 5.5 | 2.0 | 1.5 | 2.5 | 7.4 | 5.1 | 7.9 | 0.8 | 0.7 | 1.0 | 66.6 | 42.0 | 88.9 |
| WRFL | 17.0 | 11.0 | 21.5 | 0.0 | −14.5 | 13.0 | 2.0 | 1.0 | 3.5 | 1.9 | −0.1 | 3.8 | 0.6 | 0.4 | 0.8 | 84.3 | 55.0 | 117.4 |
| TGMI | 11.0 | 7.0 | 15.5 | −5.0 | −13.5 | 5.0 | 2.5 | 1.5 | 3.0 | 1.3 | −0.5 | 3.3 | 0.7 | 0.5 | 0.9 | 99.1 | 63.1 | 133.2 |
| PUMA | 9.0 | 5.0 | 12.0 | 2.5 | −4.0 | 8.0 | 2.5 | 1.5 | 3.5 | 1.0 | −1.3 | 3.6 | 0.7 | 0.5 | 0.8 | 95.6 | 61.3 | 123.7 |
| FTBA | 10.5 | 6.5 | 14.5 | 1.0 | −2.5 | 4.0 | 2.5 | 2.0 | 3.5 | 4.1 | 2.2 | 5.9 | 0.8 | 0.6 | 0.9 | 186.5 | 160.7 | 210.8 |
| PRCP | 27.0 | 22.0 | 31.5 | −1.5 | −7.5 | 7.0 | 2.5 | 1.5 | 3.5 | 0.4 | 0.0 | 0.8 | 1.0 | 1.0 | 1.0 | 61.7 | 53.6 | 67.7 |
| Correlation Coefficient | ||
|---|---|---|
| Type | Value | Reference |
| Pure rain and dry hail | >0.98 | [27] |
| Wet hail | <0.95 | [27] |
| Very large hail | <0.85 | [27] |
| Weather | >0.8 | [91] |
| Light to moderate rain | >0.99 | [91] |
| Heavy Rain | >0.97 | [91] |
| Non-meteorological | <0.85 | [30] |
| <0.80 | [27] | |
| <0.65 | [34] | |
| Biological | 0.3 to 0.5 | [36] |
| 0.5 to 0.8 | [51] | |
| 0.3 to 0.7 | [92] | |
| <0.7 | [91] | |
| Insects | 0.8 to 1 | [40] |
| 0.3 to 1.1 | [18] | |
| <0.97 | [42] | |
| 0.4 to 0.9 | [44] | |
| 0.3 to 0.8 | [91] | |
| Birds | <0.7 | [42] |
| Birds > insects | [70] | |
| Nocturnal migrating birds | 0.5 to 0.7 tail-on | [51] |
| 0.7 to 0.85 head-on | [51] | |
| Purple Martins | 0.5 to 0.8 | [51] |
| 0.3 to 1 | [18] | |
| Tree Swallows | 0.2 | [67] |
| Free-tailed Bats | 0.5 to 0.7 | [51] |
| Differential Reflectivity | ||
|---|---|---|
| Type | Value (dB) | Reference |
| Rain | 0 to 2 | [93] |
| −2 to 2 | [18] | |
| <3 | [94] | |
| Hail | Near 0 | [94] |
| Non-meteorological | >4.5 | [34] |
| Biological | >2 | [51] |
| >3 | [91] | |
| >7 | [95] | |
| Insects | 0.5 to 5 | [65] |
| 5 to 8, mean 7 | [96] | |
| 2 to 10 | [36] | |
| <10 | [97] | |
| 9 aligned | [39] | |
| 0 tail-on, head-on | [39] | |
| 0 to 3.5 | [38] | |
| 3 to 8 | [91] | |
| 4 to 6 | [92] | |
| 5 to 10 | [95] | |
| 3 to 10 | [97] | |
| about 8 | [94] | |
| 4 to 8 | [42] | |
| −4 to 8 | [18] | |
| 4 to 9 | [92] | |
| ≥8 | [68] | |
| 8 to 9 | [66] | |
| Birds | −1 to 3 | [69] |
| <4 | [98] | |
| 2.2 | [37] | |
| <2.5 | [40] | |
| −4 to 4 | [42] | |
| Nocturnal Migrating Birds | 2.5 | [99] |
| 2 to 6+ | [51] | |
| Purple Martins | 3 to 6+ | [51] |
| Tree Swallows | −8 to 4 | [67] |
| Free-tailed Bats | 1.5 to 3 | [51] |
| Backscatter Differential Phase | ||
|---|---|---|
| Type | Value (degrees) | Reference |
| Rain | 0° with 60° offset | [93] |
| Biological | 50 to 100+ | [92] |
| Insects | <40 | [69] |
| Mean 40 | [30] | |
| <20 to 30 | [98] | |
| 5–40 | [36] | |
| <30 | [37] | |
| 50 to 80 | [40] | |
| 0 to 60 | [42] | |
| 10 to 40 | [100] | |
| Birds | >100 | [69] |
| 70 to 100 | [100] | |
| 100 | [98] | |
| 0 to 100 | [36] | |
| >70 | [37] | |
| 0 to 150, most > 60 | [42] | |
| ≥100 | [68] | |
Appendix B. Supporting Figures



References
- Saltikoff, E.; Friedrich, K.; Soderholm, J.; Lengfeld, K.; Nelson, B.; Becker, A.; Hollmann, R.; Urban, B.; Heistermann, M.; Tassone, C. An overview of using weather radar for climatological studies: Successes, challenges, and potential. Bull. Am. Meteorol. Soc. 2019, 100, 1739–1752. [Google Scholar] [CrossRef]
- Chilson, P.B.; Stepanian, P.M.; Kelly, J.F. Radar Aeroecology. In Aeroecology; Chilson, P.B., Frick, W.F., Kelly, J.F., Liechti, F., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 277–309. [Google Scholar] [CrossRef]
- Chilson, P.B.; Frick, W.F.; Kelly, J.F.; Liechti, F. (Eds.) Aeroecology; Springer: Cham, Switzerland, 2018. [Google Scholar] [CrossRef]
- Bauer, S.; Shamoun-Baranes, J.; Nilsson, C.; Farnsworth, A.; Kelly, J.F.; Reynolds, D.R.; Dokter, A.M.; Krauel, J.F.; Petterson, L.B.; Horton, K.G.; et al. The grand challenges of migration ecology that radar aeroecology can help answer. Ecography 2019, 42, 861–875. [Google Scholar] [CrossRef] [Green Version]
- Shamoun-Baranes, J.; Nilsson, C.; Bauer, S.; Chapman, J. Taking radar aeroecology into the 21st century. Ecography 2019, 42, 847–851. [Google Scholar] [CrossRef]
- Schmaljohann, H. Radar aeroecology—A missing piece of the puzzle for studying the migration ecology of animals. Ecography 2020. [Google Scholar] [CrossRef]
- Jungbluth, K.; Belles, J.; Schumacher, M. Velocity contamination of WSR-88D and wind profiler data due to migrating birds. In 27th Conference on Radar Meteorology; American Meteorological Society: Vail, CO, USA, 1995; pp. 9–13. [Google Scholar]
- Gauthreaux, S.A.; Mizrahi, D.S.; Belser, C.G. Bird migration and bias of WSR-88D wind estimates. Weather Forecast 1998, 13, 465–481. [Google Scholar] [CrossRef]
- Zhang, P.; Liu, S.; Xu, Q. Identifying doppler velocity contamination caused by migrating birds. Part I: Feature extraction and quantification. J. Atmos. Ocean. Technol. 2005, 22, 1105–1113. [Google Scholar] [CrossRef]
- Holleman, I.; Van Gasteren, H.; Bouten, W. Quality assessment of weather radar wind profiles during bird migration. J. Atmos. Ocean. Technol. 2008, 25, 2188–2198. [Google Scholar] [CrossRef] [Green Version]
- Zhang, P.; Xu, Q.; Ryzhkov, A.V. Identification of biological scatterers and radar data quality control. In 21st Conf. on Several Local Storms; American Meteorological Society: San Antonio, TX, USA, 2002; pp. 208–209. [Google Scholar]
- Rennie, S.J.; Curtis, M.; Peter, J.; Seed, A.W.; Steinle, P.J.; Wen, G. Bayesian echo classification for australian single-polarization weather radar with application to assimilation of radial velocity observations. J. Atmos. Ocean. Technol. 2015, 32, 1341–1355. [Google Scholar] [CrossRef]
- Dokter, A.M.; Farnsworth, A.; Fink, D.; Ruiz-Gutierrez, V.; Hochachka, W.M.; La Sorte, F.A.; Robinson, O.J.; Rosenberg, K.V.; Kelling, S. Seasonal abundance and survival of North America’s migratory avifauna determined by weather radar. Nat. Ecol. Evol. 2018, 2, 1603–1609. [Google Scholar] [CrossRef]
- Lin, T.; Winner, K.; Bernstein, G.; Mittal, A.; Dokter, A.M.; Horton, K.G.; Nilsson, C.; Van Doren, B.M.; Farnsworth, A.; La Sorte, F.A.; et al. MistNet: Measuring historical bird migration in the US using archived weather radar data and convolutional neural networks. Methods Ecol. Evol. 2019, 10, 1908–1922. [Google Scholar] [CrossRef]
- Rosenberg, K.V.; Dokter, A.M.; Blancher, P.J.; Sauer, J.R.; Smith, A.C.; Smith, P.A.; Stanton, J.C.; Panjabi, A.; Helft, L.; Parr, M.; et al. Decline of the North American avifauna. Science 2019, 366, 120–124. [Google Scholar] [CrossRef]
- Horton, K.G.; La Sorte, F.A.; Sheldon, D.; Lin, T.-Y.; Winner, K.; Bernstein, G.; Maji, S.; Hochachka, W.M.; Farnsworth, A. Phenology of nocturnal avian migration has shifted at the continental scale. Nat. Clim. Chang. 2020, 10, 63–68. [Google Scholar] [CrossRef]
- Chilson, P.B.; Frick, W.F.; Kelly, J.F.; Howard, K.W.; Larkin, R.P.; Diehl, R.H.; Westbrook, J.K.; Kelly, T.A.; Kunz, T.H. Partly cloudy with a chance of migration: Weather, radars, and aeroecology. Bull. Am. Meteorol. Soc. 2011, 93, 669–686. [Google Scholar] [CrossRef]
- Stepanian, P.M.; Horton, K.G.; Melnikov, V.M.; Zrnić, D.S.; Gauthreaux, S.A. Dual-polarization radar products for biological applications. Ecosphere 2016, 7, e01539. [Google Scholar] [CrossRef]
- Koistinen, J. Bird migration patterns on weather radars. Phys. Chem. Earth Part B Hydrol. Ocean. Atmos. 2000, 25, 1185–1193. [Google Scholar] [CrossRef]
- Martin, W.J.; Shapiro, A. Discrimination of bird and insect radar echoes in clear air using high-resolution radars. J. Atmos. Ocean. Technol. 2007, 24, 1215–1230. [Google Scholar] [CrossRef]
- Kessinger, C.; Ellis, S.; Van Andel, J. The radar echo classifier: A fuzzy logic algorithm for the WSR-88D. In 3rd Conference on Artificial Applications to the Environmental Science; American Meteorological Society: Long Beach, CA, USA, 2003; Available online: http://ams.confex.com/ams/pdfpapers/54946.pdf (accessed on 31 January 2020).
- Liu, S.; Xu, Q.; Zhang, P. Identifying Doppler Velocity Contamination Caused by Migrating Birds. Part II: Bayes Identification and Probability Tests. J. Atmos. Ocean. Technol. 2005, 22, 1114–1121. [Google Scholar] [CrossRef]
- Gauthreaux, S.A.; Livingston, J.W.; Belser, C.G. Detection and discrimination of fauna in the aerosphere using Doppler weather surveillance radar. Integr. Comp. Biol. 2008, 48, 12–23. [Google Scholar] [CrossRef] [Green Version]
- Van Gasteren, H.; Holleman, I.; Bouten, W.; Van Loon, E.; Shamoun-Baranes, J.; Van Loon, E.E. Extracting bird migration information from C-band Doppler weather radars. Ibis 2008, 150, 674–686. [Google Scholar] [CrossRef]
- Lakshmanan, V.; Zhang, J.; Howard, K. A technique to censor biological echoes in radar reflectivity data. J. Appl. Meteorol. Clim. 2010, 49, 453–462. [Google Scholar] [CrossRef] [Green Version]
- Bringi, V.N.; Chandrasekar, V. Polarimetric Doppler Weather Radar: Principles and Applications; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Kumjian, M. Principles and applications of dual-polarization weather radar. Part I: Description of the polarimetric radar variables. J. Oper. Meteorol. 2013, 1, 226–242. [Google Scholar] [CrossRef]
- Park, H.S.; Ryzhkov, A.V.; Zrnic, D.S.; Kim, K.-E. The Hydrometeor classification algorithm for the polarimetric WSR-88D: Description and application to an MCS. Weather Forecast 2009, 24, 730–748. [Google Scholar] [CrossRef]
- Chandrasekar, V.; Keranen, R.; Lim, S.; Moisseev, D. Recent advances in classification of observations from dual polarization weather radars. Atmos. Res. 2013, 119, 97–111. [Google Scholar] [CrossRef]
- Schuur, T.; Ryzhkov, A.; Heinselman, P.; Zrnic, D.; Burgess, D.; Scharfenberg, K. Observations and Classification of Echoes with the Polarimetric WSR-88D Radar. In Report of the National Severe Storms Laboratory; National Severe Storms Laboratory: Norman, OK, USA, 2003; Volume 73069, p. 46. Available online: https://pdfs.semanticscholar.org/2d8e/5f5f5d26060726fa22b3700cfabbee043da.pdf (accessed on 5 November 2019).
- Ryzhkov, A.V.; Schuur, T.J.; Burgess, D.W.; Heinselman, P.L.; Giangrande, S.E.; Zrnic, D.S. The joint polarization experiment: Polarimetric rainfall measurements and hydrometeor classification. Bull. Am. Meteorol. Soc. 2005, 86, 809–824. [Google Scholar] [CrossRef] [Green Version]
- Lakshmanan, V.; Karstens, C.; Krause, J.; Tang, L. Quality Control of Weather Radar Data Using Polarimetric Variables. J. Atmos. Ocean. Technol. 2014, 31, 1234–1249. [Google Scholar] [CrossRef]
- Tang, L.; Zhang, J.; Langston, C.; Krause, J.; Howard, K.; Lakshmanan, V. A physically based precipitation–nonprecipitation radar echo classifier using polarimetric and environmental data in a real-time national system. Weather Forecast 2014, 29, 1106–1119. [Google Scholar] [CrossRef]
- Krause, J.M. A simple algorithm to discriminate between meteorological and nonmeteorological radar echoes. J. Atmos. Ocean. Technol. 2016, 33, 1875–1885. [Google Scholar] [CrossRef]
- Kilambi, A.; Fabry, F.; Meunier, V. A simple and effective method for separating meteorological from nonmeteorological targets using dual-polarization data. J. Atmos. Ocean. Technol. 2018, 35, 1415–1424. [Google Scholar] [CrossRef]
- Zrnic, D.; Ryzhkov, A. Observations of insects and birds with a polarimetric radar. IEEE Trans. Geosci. Remote. Sens. 1998, 36, 661–668. [Google Scholar] [CrossRef]
- Zhang, P.; Ryzhkov, A.; Zrnic, D. Detection of birds and insects using polarimetric radar observations. In 11th Conf. on Aviation, Range, and Aerospace Meteorology; CD-ROM P5.13; American Meteorological Society: Hyannis, MA, USA, 2004; pp. 897–901. Available online: https://www.semanticscholar.org/paper/Detection-of-Birds-and-Insects-Using-Polarimetric-Zhang/91cb7aff01d02c12f4f96d06350cf38820ffc068 (accessed on 31 January 2020).
- Zhang, P.F.; Ryzhkov, A.; Zrnic, D. Polarimetric prototype of the WSR-88D radar observation of birds and insects. In Preprints CD, 12th Conference on Aviation, Range, and Aerospace Meteorology; American Meteorological Society: Atlanta, GA, USA, 31 January 2006; Volume 28, Available online: https://www.semanticscholar.org/paper/P-6-.-4-POLARIMETRIC-PROTOTYPE-OF-THE-WSR-88-D-OF-Zhang-Ryzhkov/4c9b02aa1d88ed7f8c228dfb44212a30be02ee9a (accessed on 31 January 2020).
- Lang, T.J.; Rutledge, S.A.; Stith, J.L. Observations of quasi-symmetric echo patterns in clear air with the CSU–CHILL polarimetric radar. J. Atmos. Ocean. Technol. 2004, 21, 1182–1189. [Google Scholar] [CrossRef]
- Bachmann, S.; Zrnić, D. Spectral Density of Polarimetric Variables Separating Biological Scatterers in the VAD Display. J. Atmos. Ocean. Technol. 2007, 24, 1186–1198. [Google Scholar] [CrossRef] [Green Version]
- Melnikov, V.M.; Doviak, R.J.; Zrnic, D.S.; Stensrud, D.J. Mapping bragg scatter with a polarimetric WSR-88D. J. Atmos. Ocean. Technol. 2011, 28, 1273–1285. [Google Scholar] [CrossRef]
- Jiang, Y.; Xu, Q.; Zhang, P.; Nai, K.; Liu, L. Using WSR-88D polarimetric data to identify bird-contaminated doppler velocities. Adv. Meteorol. 2013, 2013, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Melnikov, V.; Leskinen, M.; Koistinen, J. Doppler Velocities at orthogonal polarizations in radar echoes from insects and birds. Geosci. Remote Sens. Lett. IEEE 2014, 11, 592–596. [Google Scholar] [CrossRef]
- Melnikov, V.M.; Istok, M.J.; Westbrook, J.K. Asymmetric radar echo patterns from insects. J. Atmos. Ocean. Technol. 2015, 32, 659–674. [Google Scholar] [CrossRef]
- Stepanian, P.M.; Horton, K.G. Extracting migrant flight orientation profiles using polarimetric radar. IEEE Trans. Geosci. Remote Sens. 2015, 53, 6518–6528. [Google Scholar] [CrossRef]
- Buler, J.J.; Randall, L.A.; Fleskes, J.P.; Barrow, W.C.; Bogart, T.; Kluver, D. Mapping wintering waterfowl distributions using weather surveillance radar. PLoS ONE 2012, 7, e41571. [Google Scholar] [CrossRef] [Green Version]
- O’Neal, B.J.; Stafford, J.D.; Larkin, R.P. Waterfowl on weather radar: Applying ground-truth to classify and quantify bird movements. J. Field Ornithol. 2010, 81, 71–82. [Google Scholar] [CrossRef]
- Randall, L.A.; Diehl, R.H.; Wilson, B.C.; Barrow, W.C.; Jeske, C.W. Potential use of weather radar to study movements of wintering waterfowl. J. Wildl. Manag. 2011, 75, 1324–1329. [Google Scholar] [CrossRef]
- Horn, J.W.; Kunz, T.H. Analyzing NEXRAD doppler radar images to assess nightly dispersal patterns and population trends in Brazilian free-tailed bats (Tadarida brasiliensis). Integr. Comp. Biol. 2008, 48, 24–39. [Google Scholar] [CrossRef] [Green Version]
- Frick, W.F.; Stepanian, P.M.; Kelly, J.F.; Howard, K.W.; Kuster, C.M.; Kunz, T.H.; Chilson, P.B. Climate and weather impact timing of emergence of bats. PLoS ONE 2012, 7, e42737. [Google Scholar] [CrossRef] [Green Version]
- Van Den Broeke, M.S. Polarimetric radar observations of biological scatterers in hurricanes Irene (2011) and Sandy (2012). J. Atmos. Ocean. Tech. 2013, 30, 2754–2767. [Google Scholar] [CrossRef] [Green Version]
- Russell, K.R.; Gauthreaux, S.A. Use of weather radar to characterize movements of roosting purple martins. Wildl. Soc. Bull. 1998, 26, 5–16. [Google Scholar]
- Russell, K.R.; Mizrahi, D.S.; Gauthreaux, S.A., Jr. Large-scale mapping of purple martin pre-migratory roosts using WSR-88D weather surveillance radar. J. Field Ornithol. 1998, 69, 316–325. [Google Scholar]
- Gauthreaux, S.; Belser, C.G. Bird migration in the region of the Gulf of Mexico. In Proceedings of the 22nd International Ornithological Congress 1999, Durban, South Africa, 16–22 August 1998; pp. 1931–1947. [Google Scholar]
- Gauthreaux, S.A., Jr. Weather radar quantification of bird migration. BioScience 1970, 20, 17–19. [Google Scholar] [CrossRef]
- Gauthreaux, S.A.; Belser, C.G. Displays of bird movements on the WSR-88D: Patterns and quantification. Weather Forecast 1998, 13, 453–464. [Google Scholar] [CrossRef]
- Jehl, J.R., Jr.; Johansson, C. Autumnal migration of Eared Grebes (Podiceps nigricollis) through southwestern Wyoming: A key to assessing the size of the North American population. Western N. Am. Nat. 2002, 62, 9. Available online: https://scholarsarchive.byu.edu/wnan/vol62/iss3/9 (accessed on 5 November 2019).
- Jehl, J.R., Jr.; Day, K.; Schmidt, B. The spectacular (and hazardous) migration of Eared Grebes (Podiceps nigricollis) through southern Utah. N. Am. Birds 2012, 66, 2–9. [Google Scholar]
- Frank, M.; Conover, M. Factors influencing the fall migration of eared grebes from Great Salt Lake. In RESEARCH WEEK 2015; Utah State University: Logan, UT, USA, 2015; Available online: https://digitalcommons.usu.edu/researchweek/ResearchWeek2015/All2015/76/ (accessed on 5 November 2019).
- Williams, A.A.; Laird, N.F. Weather and eared grebe winter migration near the Great Salt Lake, Utah. Int. J. Biometeorol. 2018, 62, 433–447. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Cutler, D.R.; Edwards, T.C., Jr.; Beard, K.H.; Cutler, A.; Hess, K.T.; Gibson, J.; Lawler, J.J. Random forests for classification in ecology. Ecology 2007, 88, 2783–2792. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2012; Available online: https://www.R-project.org/ (accessed on 31 January 2020).
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic Minority Over-sampling Technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- Mueller, E.A.; Larkin, R.P. Insects observed using dual-polarization radar. J. Atmos. Ocean. Technol. 1985, 2, 49–54. [Google Scholar] [CrossRef] [Green Version]
- Achtemeier, G.L. The use of insects as tracers for “clear-air” boundary-layer studies by doppler radar. J. Atmos. Ocean. Tech. 1991, 8, 746–765. [Google Scholar] [CrossRef]
- Muller, B.; Mosher, F.; Herbster, C.; Brickhouse, A. Aviation bird hazard in NEXRAD dual polarization weather radar confirmed by visual observations. Int. J. Aviat. Aeronaut. Aerosp. 2015, 2, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Chilson, C.; Avery, K.; McGovern, A.; Bridge, E.; Sheldon, D.; Kelly, J. Automated detection of bird roosts using NEXRAD radar data and Convolutional Neural Networks. Remote Sens. Ecol. Cons. 2019, 5, 20–32. [Google Scholar] [CrossRef]
- McCracken, G.F.; Gillam, E.H.; Westbrook, J.K.; Lee, Y.F.; Jensen, M.L.; Balsley, B.B. Brazilian free-tailed bats (Tadarida brasiliensis: Molossidae, Chiroptera) at high altitude: Links to migratory insect populations. Integr. Comp. Biol. 2008, 48, 107–118. [Google Scholar] [CrossRef] [Green Version]
- Jatau, P.; Melnikov, V. Bird detection algorithm for the WSR-88D radars. In Report on Radar Operations Center Memorandum of Understanding Task 14; University of Oklahoma, Cooperative Institute for Mesoscale Meteorological Studies: Norman, OK, USA, 2018. Available online: https://www.nssl.noaa.gov/publications/wsr88d_reports/BirdDetectionAlgorithm_2018.pdf (accessed on 5 November 2019).
- Zrnic, D.S.; Ryzhkov, A.V. Polarimetry for weather surveillance radars. Bull. Am. Meteorol. Soc. 1999, 80, 389–406. [Google Scholar] [CrossRef]
- Mirkovic, D.; Stepanian, P.M.; Kelly, J.F.; Chilson, P.B. Electromagnetic model reliably predicts radar scattering characteristics of airborne organisms. Sci. Rep. UK 2016, 6, 35637. [Google Scholar] [CrossRef]
- Shipley, J.R.; Kelly, J.F.; Frick, W.F. Toward integrating citizen science and radar data for migrant bird conservation. Remote Sens. Ecol. Cons. 2018, 4, 127–136. [Google Scholar] [CrossRef]
- Horton, K.G.; Van Doren, B.M.; La Sorte, F.A.; Fink, D.; Sheldon, D.; Farnsworth, A.; Kelly, J.F. Navigating north: How body mass and winds shape avian flight behaviours across a North American migratory flyway. Ecol. Lett. 2018, 21, 1055–1064. [Google Scholar] [CrossRef] [PubMed]
- Horton, K.G.; Van Doren, B.M.; La Sorte, F.A.; Cohen, E.B.; Clipp, H.L.; Buler, J.J.; Fink, D.; Kelly, J.F.; Farnsworth, A. Holding steady: Little change in intensity or timing of bird migration over the Gulf of Mexico. Glob. Chang. Boil. 2019, 25, 1106–1118. [Google Scholar] [CrossRef] [PubMed]
- Donnelly, J.P.; Naugle, D.E.; Collins, D.P.; Dugger, B.D.; Allred, B.W.; Tack, J.D.; Dreitz, V.J. Synchronizing conservation to seasonal wetland hydrology and waterbird migration in semi-arid landscapes. Ecosphere 2019, 10, e02758. [Google Scholar] [CrossRef]
- Meade, J.; Van Der Ree, R.; Stepanian, P.M.; Westcott, D.A.; Welbergen, J.A. Using weather radar to monitor the number, timing and directions of flying-foxes emerging from their roosts. Sci. Rep. 2019, 9, 10222. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Arnett, E.B.; Huso, M.M.; Schirmacher, M.R.; Hayes, J.P. Altering turbine speed reduces bat mortality at wind-energy facilities. Front. Ecol. Environ. 2010, 9, 209–214. [Google Scholar] [CrossRef] [Green Version]
- Schmaljohann, H.; Liechti, F.; Bächler, E.; Steuri, T.; Bruderer, B. Quantification of bird migration by radar —A detection probability problem. Ibis 2008, 150, 342–355. [Google Scholar] [CrossRef]
- Horton, K.G.; Shriver, W.G.; Buler, J.J. A comparison of traffic estimates of nocturnal flying animals using radar, thermal imaging, and acoustic recording. Ecol. Appl. 2015, 25, 390–401. [Google Scholar] [CrossRef]
- Drake, V.A. Distinguishing target classes in observations from vertically pointing entomological radars. Int. J. Remote Sens. 2016, 37, 3811–3835. [Google Scholar] [CrossRef]
- Wang, R.; Hu, C.; Fu, X.; Long, T.; Zeng, T. Micro-Doppler measurement of insect wing-beat frequencies with W-band coherent radar. Sci. Rep. 2017, 7, 1396. [Google Scholar] [CrossRef] [Green Version]
- Radhakrishna, B.; Fabry, F.; Kilambi, A. Fuzzy logic algorithms to identify birds, precipitation, and ground clutter in s-band radar data using polarimetric and nonpolarimetric variables. J. Atmos. Ocean. Technol. 2019, 36, 2401–2414. [Google Scholar] [CrossRef]
- Van Gasteren, H.; Krijgsveld, K.L.; Klauke, N.; Leshem, Y.; Metz, I.C.; Skakuj, M.; Sorbi, S.; Schekler, I.; Shamoun-Baranes, J. Aeroecology meets aviation safety: Early warning systems in Europe and the Middle East prevent collisions between birds and aircraft. Ecography 2019, 42, 899–911. [Google Scholar] [CrossRef]
- Leskinen, M.; Markkula, I.; Koistinen, J.; Pylkkö, P.; Ooperi, S.; Siljamo, P.; Ojanen, H.; Raiskio, S.; Tiilikkala, K. Pest insect immigration warning by an atmospheric dispersion model, weather radars and traps. J. Appl. Entomol. 2011, 135, 55–67. [Google Scholar] [CrossRef] [Green Version]
- Gauthreaux, S.A.; Belser, C.G. Radar ornithology and biological conservation. Auk 2003, 120, 266–277. [Google Scholar] [CrossRef]
- Hüppop, O.; Ciach, M.; Diehl, R.; Reynolds, D.R.; Stepanian, P.M.; Menz, M.H.M. Perspectives and challenges for the use of radar in biological conservation. Ecography 2019, 42, 912–930. [Google Scholar] [CrossRef]
- Bauer, S.; Chapman, J.W.; Reynolds, D.R.; Alves, J.A.; Dokter, A.M.; Menz, M.M.H.; Sapir, N.; Ciach, M.; Pettersson, L.B.; Kelly, J.F.; et al. From agricultural benefits to aviation safety: Realizing the potential of continent-wide radar networks. Bioscience 2017, 67, 912–918. [Google Scholar] [CrossRef]
- Zrnic, D.S.; Kimpel, J.F.; Forsyth, D.E.; Shapiro, A.; Crain, G.; Ferek, R.; Heimmer, J.; Benner, W.; McNellis, T.J.; Vogt, R.J. Agile-beam phased array radar for weather observations. Bull. Am. Meteorol. Soc. 2007, 88, 1753–1766. [Google Scholar] [CrossRef]
- Zhang, G.; Mahale, V.N.; Putnam, B.J.; Qi, Y.; Cao, Q.; Byrd, A.D.; Bukovcic, P.; Zrnic, D.S.; Gao, J.; Xue, M.; et al. Current status and future challenges of weather radar polarimetry: Bridging the gap between radar meteorology/hydrology/engineering and numerical weather prediction. Adv. Atmos. Sci. 2019, 36, 571–588. [Google Scholar] [CrossRef] [Green Version]
- Wen, G.; Protat, A.; Xiao, H. An objective prototype-based method for dual-polarization radar clutter identification. Atmosphere 2017, 8, 72. [Google Scholar] [CrossRef] [Green Version]
- Melnikov, V.; Zrnic, D.S. Observations of convective thermals with weather radar. J. Atmos. Ocean. Technol. 2017, 34, 1585–1590. [Google Scholar] [CrossRef]
- Balakrishnan, N.; Zrnic, D.S. Use of polarization to characterize precipitation and discriminate large hail. J. Atmos. Sci. 1990, 47, 1525–1540. [Google Scholar] [CrossRef]
- Browning, K.A.; Nicol, J.C.; Marsham, J.H.; Rogberg, P.; Norton, E.G. Layers of insect echoes near a thunderstorm and implications for the interpretation of radar data in terms of airflow. Q. J. R. Meteorol. Soc. 2011, 137, 723–735. [Google Scholar] [CrossRef]
- Buban, M.S.; Ziegler, C.L.; Rasmussen, E.N.; Richardson, Y.P. The dryline on 22 May 2002 during IHOP: Ground-radar and in situ data analyses of the dryline and boundary layer evolution. Mon. Weather Rev. 2007, 135, 2473–2505. [Google Scholar] [CrossRef]
- Wilson, J.W.; Weckwerth, T.M.; Vivekanandan, J.; Wakimoto, R.M.; Russell, R.W. Boundary layer clear-air radar echoes: Origin of echoes and accuracy of derived winds. J. Atmos. Ocean. Technol. 1994, 11, 1184–1206. [Google Scholar] [CrossRef] [Green Version]
- Bachmann, S.; Zrnic, D. Spectral polarimetry for identifying and separating mixed biological scatters. In Proceedings of the 32nd International Conference on Radar Meteorology, Albuquerque, NM, USA, 27 October 2005; P9R.5. Available online: https://www.semanticscholar.org/paper/Spectral-polarimetry-for-identifing-and-separating-Bachmann/fa7698e7e4317b8698a1d83a1777c95f0c41c1d1 (accessed on 31 January 2020).
- Ryzhkov, A.V.; Janish, J.M.; Schuur, T.J.; Zhang, P.; Elmore, K.L. Dual-polarization radar as a tool for operational identification of different types of meteorological and non-meteorological targets. In Proceedings of the 13th Conference on Applied Climatology and the 10th Conference on Aviation, Range, and Aerospace Meteorology, Portland, OR, USA, 13–16 May 2002; pp. 104–107. [Google Scholar]
- Vaughn, C.R. Birds and insects as radar targets: A review. Proc. IEEE 1985, 73, 205–227. [Google Scholar] [CrossRef]
- Zrnic, V.M.D.S.; Zrnic, D.; Melnikov, V.; Ryzhkov, A. Use of backscatter differential phase in weather surveillance radars. In Proceedings of the 2004 IEEE International Geoscience and Remote Sensing Symposium, Anchorage, AK, USA, 20–24 September 2004; Volume 1, pp. 456–458. [Google Scholar] [CrossRef]





| Aggregation 1 | Sample Size 2 (RV/Sweeps/Radars) | Description | ||
|---|---|---|---|---|
| Low | Medium | High | ||
| Trans-gulf migrants (TGMI) | vertebrates | biological | 1,522,978/30/5 | Songbird-dominated migration over open water of the Gulf |
| Purple martins (PUMA) | vertebrates | biological | 47,620/13/11 | Morning roost departure |
| Waterfowl (WRFL) | vertebrates | biological | 162,870/11/4 | Ducks, geese, some cranes; migratory departure |
| Eared grebes (EAGR) | vertebrates | biological | 21,815/14/1 | Migratory departure nearly due south out of Great Salt Lake |
| Free-tailed bats (FTBA) | vertebrates | biological | 49,049/11/5 | Evening roost departure |
| Aerial plankton (ISCT) | arthropods | biological | 1,208,953/15/11 | Broad-front diurnal insect movement |
| Mayflies, midges (SWRM) | arthropods | biological | 98,354/21/3 | Mating swarms |
| Precipitation (PRCP) | precipitation | precipitation | 1,374,235/15/12 | Light to moderate rain |
| Aggregation | Classes | Variables | Description/Notes |
|---|---|---|---|
| High | biological–precipitation | ZH, Vr, σV, ZDR, ρHV, ΦDP | aggregates six biological classes |
| Medium | vertebrates–arthropods–precipitation | ZH, Vr, σV, ZDR, ρHV, ΦDP | aggregates 4 vertebrate and 2 arthropod classes |
| vertebrates–arthropods–precipitation | ZH, Vr, σV | as above, original variables only | |
| vertebrates–arthropods–precipitation | ZDR, ρHV, ΦDP | as above, polarimetry variables only | |
| vertebrates–arthropods | ZH, Vr, σV, ZDR, ρHV, ΦDP | as above, sans precipitation | |
| vertebrates–other | ZH, Vr, σV, ZDR, ρHV, ΦDP | “other” equally under-samples arthropods and precipitation | |
| arthropods–other | ZH, Vr, σV, ZDR, ρHV, ΦDP | “other” equally under-samples vertebrates and precipitation | |
| precipitation–other | ZH, Vr, σV, ZDR, ρHV, ΦDP | “other” equally under-samples vertebrates and arthropods | |
| Low | SWRM–ISCT–WRFL–TGMI–PUMA–FTBA–PRCP | ZH, Vr, σV, ZDR, ρHV, ΦDP | biological classes considered together in multinomial models |
| SWRM–ISCT–WRFL–TGMI–PUMA–FTBA–PRCP | ZH, Vr, σV | as above, original variables only | |
| SWRM–ISCT–WRFL–TGMI–PUMA–FTBA–PRCP | ZDR, ρHV, ΦDP | as above, polarimetry variables only | |
| TGMI–ISCT | ZH, Vr, σV, ZDR, ρHV, ΦDP | common discrimination problem | |
| Scatterer 1–other | ZH, Vr, σV, ZDR, ρHV, ΦDP | “other” equally under-samples non-SWRM classes | |
| EAGR–other | ZH, Vr, σV, ZDR, ρHV, ΦDP, AZ, RA | as above, includes azimuth (AZ) and range (RA) as variables |
| a. High Aggregation | ||
| Biological | Precip | |
| Biological | 98.7 | 1.3 |
| Precip | 2.2 | 97.8 |
| b. Medium Aggregation | ||
| Taxa | Other | |
| Vertebrates | 94.8 | 5.2 |
| Other | 6.8 | 93.2 |
| Arthropods | 93.5 | 6.5 |
| Other | 5.4 | 94.6 |
| Vertebrates | Arthropods | |
| Vertebrates | 94.3 | 5.7 |
| Arthropods | 7.3 | 92.7 |
| Taxa | Other | |
|---|---|---|
| ISCT | 93.0 | 7.0 |
| Other | 5.7 | 94.3 |
| FTBA | 92.2 | 7.8 |
| Other | 8.2 | 91.8 |
| SWRM | 95.2 | 4.8 |
| Other | 3.9 | 96.1 |
| TGMI | 86.9 | 13.1 |
| Other | 19.0 | 81.0 |
| PUMA | 90.5 | 9.5 |
| Other | 18.2 | 81.8 |
| WRFL | 87.7 | 12.3 |
| Other | 12.7 | 87.3 |
| TGMI | 95.8 | 4.2 |
| ISCT | 6.1 | 93.9 |
| a. All variables | ||||||||
| SWRM | ISCT | WRFL | TGMI | PUMA | FTBA | PRCP | Error | |
| SWRM | 90.3 | 3.9 | 1.8 | 1.4 | 1.8 | 0.4 | 0.5 | 9.7 |
| ISCT | 2.1 | 87.9 | 0.7 | 1.5 | 5.8 | 1.9 | 0.1 | 12.1 |
| WRFL | 2.4 | 1.5 | 71.6 | 11.4 | 9.9 | 2.0 | 1.2 | 28.4 |
| TGMI | 2.1 | 2.4 | 11.7 | 59.4 | 18.7 | 5.2 | 0.5 | 40.6 |
| PUMA | 1.5 | 5.6 | 4.5 | 10.3 | 68.8 | 8.7 | 0.5 | 31.2 |
| FTBA | 1.0 | 2.6 | 1.2 | 3.7 | 8.9 | 82.5 | 0.1 | 17.5 |
| PRCP | 0.6 | 0.2 | 1.7 | 0.6 | 0.7 | 0.1 | 96.2 | 3.8 |
| EC | 1.8 | 2.5 | 1.7 | 2.6 | 7.3 | 1.9 | 0.5 | |
| b. Legacy Variables | ||||||||
| SWRM | ISCT | WRFL | TGMI | PUMA | FTBA | PRCP | Error | |
| SWRM | 72.3 | 6.9 | 1.3 | 2.3 | 2.6 | 8.4 | 6.1 | 27.7 |
| ISCT | 0.9 | 72.7 | 0.7 | 2.7 | 8.1 | 14.8 | 0.1 | 27.3 |
| WRFL | 9.8 | 4.2 | 42.8 | 14.3 | 8.9 | 9.6 | 10.5 | 57.2 |
| TGMI | 7.1 | 7.0 | 11.5 | 36.9 | 13.5 | 21.9 | 2.2 | 63.1 |
| PUMA | 1.9 | 17.7 | 1.7 | 7.4 | 37.2 | 32.4 | 1.7 | 62.8 |
| FTBA | 6.4 | 12.2 | 1.3 | 2.9 | 11.9 | 63.2 | 2.1 | 36.8 |
| PRCP | 23.9 | 0.6 | 7.5 | 3.2 | 3.6 | 5.5 | 55.7 | 44.3 |
| EC | 6.8 | 7.0 | 1.5 | 3.0 | 8.5 | 12.2 | 2.2 | |
| c. Dual-Pol Variables | ||||||||
| SWRM | ISCT | WRFL | TGMI | PUMA | FTBA | PRCP | Error | |
| SWRM | 60.0 | 23.1 | 7.6 | 3.5 | 1.4 | 3.4 | 1.1 | 40.0 |
| ISCT | 15.6 | 65.0 | 10.3 | 4.2 | 3.0 | 1.1 | 0.9 | 35.0 |
| WRFL | 5.3 | 6.8 | 53.5 | 13.4 | 13.2 | 6.7 | 1.2 | 46.5 |
| TGMI | 4.9 | 6.4 | 28.4 | 32.6 | 16.8 | 6.7 | 4.2 | 67.4 |
| PUMA | 3.0 | 8.6 | 32.7 | 17.7 | 27.7 | 8.9 | 1.5 | 72.3 |
| FTBA | 4.4 | 3.1 | 11.1 | 8.0 | 3.7 | 69.5 | 0.2 | 30.5 |
| PRCP | 0.9 | 0.3 | 1.6 | 2.0 | 0.9 | 0.1 | 94.2 | 5.8 |
| EC | 4.6 | 6.6 | 10.7 | 6.1 | 3.3 | 5.0 | 1.1 | |
| a. All variables | ||||
| Vertebrates | Arthropods | Precip. | Error | |
| Vertebrates | 93.1 | 5.6 | 1.3 | 6.9 |
| Arthropods | 6.8 | 92.7 | 0.5 | 7.3 |
| Precip. | 1.7 | 0.7 | 97.5 | 2.5 |
| b. Legacy variables | ||||
| Vertebrates | Arthropods | Precip. | Error | |
| Vertebrates | 76.4 | 14.0 | 9.6 | 23.6 |
| Arthropods | 20.3 | 66.7 | 13.0 | 33.3 |
| Precip. | 14.5 | 11.4 | 74.1 | 25.9 |
| c. Dual-pol variables | ||||
| Vertebrates | Arthropods | Precip. | Error | |
| Vertebrates | 84.0 | 13.2 | 2.8 | 16.0 |
| Arthropods | 14.9 | 83.7 | 1.4 | 16.3 |
| Precip. | 3.1 | 1.2 | 95.7 | 4.3 |
| EAGR | Other | |
| EAGR | 97.5 | 2.5 |
| Other | 6.1 | 93.9 |
| EAGR | Other | |
| EAGR | 99.8 | 0.2 |
| Other | 0.3 | 99.7 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gauthreaux, S.; Diehl, R. Discrimination of Biological Scatterers in Polarimetric Weather Radar Data: Opportunities and Challenges. Remote Sens. 2020, 12, 545. https://doi.org/10.3390/rs12030545
Gauthreaux S, Diehl R. Discrimination of Biological Scatterers in Polarimetric Weather Radar Data: Opportunities and Challenges. Remote Sensing. 2020; 12(3):545. https://doi.org/10.3390/rs12030545
Chicago/Turabian StyleGauthreaux, Sidney, and Robert Diehl. 2020. "Discrimination of Biological Scatterers in Polarimetric Weather Radar Data: Opportunities and Challenges" Remote Sensing 12, no. 3: 545. https://doi.org/10.3390/rs12030545
APA StyleGauthreaux, S., & Diehl, R. (2020). Discrimination of Biological Scatterers in Polarimetric Weather Radar Data: Opportunities and Challenges. Remote Sensing, 12(3), 545. https://doi.org/10.3390/rs12030545