Next Article in Journal
Use of Hyperion for Mangrove Forest Carbon Stock Assessment in Bhitarkanika Forest Reserve: A Contribution Towards Blue Carbon Initiative
Next Article in Special Issue
The Morphology of Evolved Urban Fabric around Farm Ponds
Previous Article in Journal
Quantitative Evaluation of Environmental Loading Induced Displacement Products for Correcting GNSS Time Series in CMONOC
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 12
Issue 4
10.3390/rs12040595
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Assessing Terrestrial Ecosystem Resilience using Satellite Leaf Area Index

by
Jinhui Wu
1 and
Shunlin Liang
2,*
1
State Key Laboratory of Remote Sensing Science, Faculty of Geography Science, Beijing Normal University, Beijing 100875, China
2
Department of Geographical Sciences, University of Maryland, College Park, MD 20742, USA
*
Author to whom correspondence should be addressed.
Remote Sens. 2020, 12(4), 595; https://doi.org/10.3390/rs12040595
Submission received: 6 January 2020 / Revised: 5 February 2020 / Accepted: 6 February 2020 / Published: 11 February 2020
(This article belongs to the Special Issue Remote Sensing of Environmental Health Resilience)
Browse Figures
Versions Notes

Abstract

:
Quantitative approaches to measuring and assessing terrestrial ecosystem resilience, which expresses the ability of an ecosystem to recover from disturbances without shifting to an alternative state or losing function and services, is critical and essential to forecasting how terrestrial ecosystems will respond to global change. However, global and continuous terrestrial resilience measurement is fraught with difficulty, and the corresponding attribution of resilience dynamics is lacking in the literature. In this study, we assessed global terrestrial ecosystem resilience based on the long time-series GLASS LAI product and GIMMS AVHRR LAI 3g product, and validated the results using drought and fire events as the main disturbance indicators. We also analyzed the spatial and temporal variations of global terrestrial ecosystem resilience and attributed their dynamics to climate change and environmental factors. The results showed that arid and semiarid areas exhibited low resilience. We found that evergreen broadleaf forest exhibited the highest resilience (mean resilience value (from GLASS LAI): 0.6). On a global scale, the increase of mean annual precipitation had a positive impact on terrestrial resilience enhancement, while we found no consistent relationships between mean annual temperature and terrestrial resilience. For terrestrial resilience dynamics, we observed three dramatic raises of disturbance frequency in 1989, 1995, and 2001, respectively, along with three significant drops in resilience correspondingly. Our study mapped continuous spatiotemporal variation and captured interannual variations in terrestrial ecosystem resilience. This study demonstrates that remote sensing data are effective for monitoring terrestrial resilience for global ecosystem assessment.

Graphical Abstract

1. Introduction

Terrestrial ecosystems face increasing pressure from both climate change and anthropogenic activities [1,2,3]. As many environmental components are changing, it is less likely that an ecosystem will remain unaffected. Thus, explaining the trends and processes of ecosystem changes within the context of large-scale alterations of environmental conditions constitutes a research priority of global relevance [4,5]. The concept of resilience has been proposed to analyze the response of ecosystems to short-term climatic disturbances [6]. Resilience is quantified by measuring the rate of the ecosystem required to return the ecosystem to the state that existed before the stress [7], and it generally focuses on the disturbance from which the ecosystem could recover to its original state without leading to ecosystem shift to an alternative state [6,8]. Many studies have quantified terrestrial ecosystem resilience using in-situ data [9,10,11,12,13]. Field-measurement-based studies can have high accuracy and reliability. However, these methods have been applied mainly at the regional scale, and global resilience measurement is almost absent from the literature.
Remote sensing can provide information over broad spatial extents that is difficult or impossible to obtain from field studies [14]. Moreover, continuous remote sensing data, obtained over several decades, enable the terrestrial ecosystem resilience measurement of long time-series [15]. Because of the characteristics of remote sensing and the key role of vegetation in ecosystems, vegetation has generally been the main object of satellite-based terrestrial resilience measurements [16]. Until recently, satellite-based resilience measurements have been focused mainly on the recovery capability of ecosystems to a specific type of disturbance. These methods generally detect the disturbance first then monitor the response of vegetation. Ecosystem recovery capability from fire has been widely studied in many types of terrestrial ecosystems [17,18,19], and measuring ecosystem recovery capability from drought is becoming a hot area of research [20]. In addition, various types of ecosystem resilience to other disturbances have also been studied extensively [9,21,22]. Compared with field-measurement-based research, remote sensing data increase the spatial coverage of resilience measurement. However, remote-sensing-based studies that measure terrestrial resilience from one specific type of disturbance are imperfect because ecosystems typically are being disturbed continuously, and because multiple disturbances may have an interactive effect on the ecosystem. Thus, detecting a complete disturbance and capturing the corresponding ecosystem anomaly are laborious tasks to achieve, especially at a global scale.
To determine terrestrial ecosystem recovery capability to multiple disturbances, several studies have directly detected anomalies of vegetation from remote sensing data to measure terrestrial ecosystem resilience. Global engineering resilience has been mapped using the satellite Normalized Difference Vegetation Index (NDVI) and reanalysis data [23]. Harris et al. used the length of time for vegetation to recover from disturbances as an indicator of ecosystem resilience and investigated spatial and temporal patterns of resilience of vegetation across southern Africa (1982–2006) [24]. Moreover, recent studies have developed several satellite-based indexes, which have been demonstrated to be potential key components of resilience. Seddon et al. [25] developed the Vegetation Sensitivity Index (VSI), which identified the global terrestrial resilience of ecosystems during the period of 2000–2013. Verbesselt et al. [26] measured the resilience of tropical forests using the temporal autocorrelation of vegetation based on the critical slowing down theory. These studies enabled measurement of global resilience, but the results are multiyear average values that cannot characterize the resilience variation or underlying causes.
In this study, we measured terrestrial ecosystem resilience by monitoring vegetation anomalies caused by disturbances. Because of the characteristics of the remote sensing data, this study focused only on disturbances that could lead to changes in vegetation. Resilience is related to the maximum stress from which an ecosystem can recover and is negatively correlated with the time it takes for an ecosystem to recover from disturbance [27,28]. Thus, we characterized the maximum stress from which an ecosystem can recover (Ms) and the time required for the ecosystem to recover from this maximum stress (Rt) as a ratio to measure terrestrial resilience [29]. Because Leaf Area Index (LAI) was directly estimated from remote sensing data using physical models, and LAI exhibited high accuracy for vegetation monitoring, we selected two LAI datasets (GLASS AVHRR LAI product and GIMMS AVHRR LAI 3g product) and two disaster factors (drought and fire) in this study to monitor vegetation anomalies, measure terrestrial ecosystem resilience, and analyze spatiotemporal variation. Overall, this study had three specific objectives: (1) to map global terrestrial ecosystem resilience using an advanced remote sensing product, (2) to characterize the spatiotemporal variations of global terrestrial ecosystem resilience, and (3) to analyze impact of potential drivers on terrestrial resilience distribution and variation.

2. Materials and Methods

2.1. Remote Sensing Data

The Global LAnd Surface Satellite (GLASS) LAI dataset with Advanced Very High-Resolution Radiometer (AVHRR) reflectance data, acquired from the Beijing Normal University, was used for this study [30,31,32] (Table 1). This long time-series data spanned from 1982 to 2016 at a spatial resolution of 0.05° over an eight-day interval. In the GLASS LAI dataset, the physical methods are based on the inversion of canopy radiative transfer models through general regression neural networks (GRNNs). The GLASS LAI are both spatially and temporally continuous compared with other global remote-sensing LAI products. Moreover, the GLASS LAI dataset provides the longest time series, approximately four decades, and has been widely used for global vegetation monitoring and ecosystem assessment [33,34,35].
The Global Inventory Monitoring and Modeling System (GIMMS 3g) LAI dataset with an Advanced Very High-Resolution Radiometer (AVHRR), acquired from the National Oceanographic and Atmospheric Administration (NOAA), was also used for the analysis. The GIMMS AVHRR LAI 3g dataset spanned from 1982 to 2011 at a spatial resolution of 0.083° and a 15-day interval [36]. The GIMMS AVHRR LAI 3g selected the latest version, termed the third generation NDVI dataset (GIMMS NDVI3g) as input data, which specifically aims to improve data quality in the high latitudes where the growing season is shorter than two months. It has also improved calibration that is tied to the Sea-Viewing Wide-Field-of-View Sensor, as opposed to earlier versions of GIMMS NDVI datasets that were based on inter-calibration with the Systeme Probatoire d’Observation de la Terre (SPOT) sensor. Moreover, the maximum value composite (MVC) method was adopted to remove atmosphere noise. The GIMMS AVHRR LAI 3g dataset is one of the high-quality global LAI datasets [4,32].
Fire data were acquired from the Along Track Scanning Radiometer (ATSR) World Fire Atlas (WFA). The ATSR-WFA provides a global fire monitoring service by using data acquired by the ATSR-2 and AATSR sensors from European Space Agency satellites. ATSR-WFA spanned from 1995 to 2012 at a spatial resolution of 0.05° over a one month interval [37]. This dataset consists of two versions which were developed based on two different algorithms [38]. The version of algorithm 1 was used for disturbance detection in this study.
Land-cover data were obtained from Global Mosaics of the standard Moderate-resolution Imaging Spectroradiometer (MODIS) land cover type data product (MCD12Q1) for statistical analysis in this study [39]. The dataset boundaries are -180.0° <= longitude <= 180.0°; -64.0° <= latitude <= 84.0°. The MCD12Q1 dataset spans 2001 to 2012 at an annual time step. The land-cover dataset has two version of spatial resolution, 5’ * 5’ and 0.5° * 0.5°, and the version of 0.5° spatial resolution was used for analysis in this study. This dataset consists of 17 general land-cover types, which includes 11 natural vegetation classes, three developed and mosaicked land classes and three nonvegetated land classes [40,41].

2.2. Climate and Soil Data

Droughts were quantified using monthly time-series data from the Self-Calibrating Palmer Drought Severity Index (SC-PDSI) based on the Climatic Research Unit (CRU) TS3.10.01 datasets from 2000 to 2009 at a 0.5° resolution [42]. The SC-PDSI replaced the empirically derived climatic characteristic (K) and duration factors with values calculated automatically based on the historic climatic data of a specific location [43]. The computation of the SC-PDSI involves the classification of relative soil moisture conditions within 11 categories: extremely wet, severely wet, moderately wet, slightly wet, incipient wet spell, near normal, incipient dry spell, slightly dry, moderately dry, severely dry, and extremely dry [44].
Mean annual precipitation (MAP) and mean annual temperature (MAT) used in this study were extracted from the monthly precipitation and monthly temperature datasets in the Climate Research Unit (CRU) [45] version TS4.01, which spanned the 20th century and, therefore, covered our study period (1982-2011) with a spatial resolution of 0.5°. MAP was calculated by summing monthly precipitation to generate annual precipitation then averaging the annual precipitation. MAT was calculated by averaging the monthly temperature to generate the annual temperature then averaging the annual temperature. The gridded datasets were obtained from more than 4000 meteorological stations and interpolated based on spatial autocorrelation functions [46,47]. These climate datasets were thoroughly evaluated and applied in global ecology and climate studies [48,49,50,51].
Soil moisture data were obtained from the United States Department of Agriculture-Natural Resources Conservation Service (USDA-NRCS) for statistical analysis in this study [52]. The global soil moisture regime data are based on an interpolation of over 20,000 climatic stations that were input into a soil water balance model to estimate soil moisture regimes. The soil moisture regime map data are rasterized on a 2-min grid cell. This soil moisture data provide one of the few high-quality soil moisture datasets on a global scale.

2.3. Methods

2.3.1. Data Preprocessing

To match all data we used in this study, we interpolated all datasets to a spatial resolution of 0.5°. For fire data, we calculated the proportion of the fire area in each area of 0.5° * 0.5°. For the other data, we used bilinear interpolation for resampling. Averaging on a pixel level to coarser spatial resolutions is helpful for reducing data noise because the noise would be offset in the process of up-scaling the resample [53].
As our study concentrated on only the disturbance that did not lead to ecosystem regime changes, we derived the LAI grids, where the land-cover type was unchanged, from the GLASS LAI and GIMMS AVHRR LAI 3g datasets for further analysis. An unchanged pixel is defined as a pixel always being the same land-cover type during the 2001-2012 period. To diminish the impacts of disturbances caused by human activities, the grids that had urban and built-up land-cover type were excluded in further statistical analysis.
To increase the signal-to-noise ratio without greatly distorting the signal, a Savitzky–Golay filter was used pixel by pixel for smoothing long time-series data before calculating resilience index [54,55,56,57,58]. In this study, we set the half-width of the smoothing window size to 3 to get a smoother result and a higher computational efficiency.

2.3.2. A Satellite-Based Terrestrial Resilience Index

In this study, LAI was selected as the proxy of vegetation to measure the terrestrial resilience because of its high accuracy on vegetation monitoring. Based on the concept of resilience which has been put forward [54,55], we characterized terrestrial resilience as a ratio of the magnitude of maximum stress from which the LAI can recover (Ms) to the length of time (Rt) required for the LAI to recover to its normal range. This index only focuses on the disturbances that lead to vegetation that is worse than the normal level, and that do not cause ecosystem regime shifts [19,54].
We defined the LAI anomalies caused by disturbances that occurred when the LAI became lower than its normal range. We used the mean and the standard deviation of LAI to scope the normal variation range. In the period where the LAI was below the normal range, we detected the lowest LAI and marked this time point as the starting point for recovery. At this time point, the difference value between the lowest LAI and the normal range was defined as Ms (Figure 1), which denotes the maximum stress from which an ecosystem can endure and recover. The time point where the LAI came back to the normal range was defined as the end point of recovery, and the time span between start point and end point was defined as Rt. These two components were combined into an overall definition of terrestrial resilience. The ratio of Ms to Rt was defined as the terrestrial ecosystem resilience of the start time point. The time-series LAI was continuously detected to find the next anomaly from the time point behind the last end point.
The time and duration of anomalies are different, indicating that in some years several anomalies occur while in some years no anomalies occur. Some rules were set up for annual terrestrial resilience calculation: The resilience values for which the recovery time crossed more than one year belonged to the resilience of the start point (Figure 2). The resilience values for years where no anomaly was found, or where the last recovery process covered the entire year, were set as equal to the resilience value of the last year. The annual resilience values of years where more than one anomaly was found were calculated by averaging the values of resilience detected in the year.
The fluctuation amplitude of vegetation in different land-cover types were various when disturbances occurred. Meanwhile, we found that large numbers of anomalies caused by disturbances were neglected when we used standard deviations of LAI in different land-cover types. To include more LAI anomalies caused by disturbances and exclude the LAI anomalies caused by data noise, a parameter (β) was integrated into the equation to adjust the normal range for different land-cover types:
M s = M E A N j   −   L A I i j ( l o w e s t ) − β × S T D j R e s i l i e n c e = M s / R t
where M s is the maximum amplitude of LAI when it is below the normal range, denoting the maximum stress from which an ecosystem can endure and recover; L A I i j ( l o w e s t ) is the LAI in month j and year i , which is the lowest LAI in the period of anomaly; M E A N j is the month j mean LAI in recent decades (1982-2016 for GLASS LAI, 1982-2011 for GIMMS AVHRR LAI 3g); β is the parameter used to adjust the normal range; S T D j is the month j LAI standard deviation in recent decades (1982-2016 for GLASS LAI, 1982-2011 for GIMMS AVHRR LAI 3g); and R t is the length of time required for the LAI value to recover to its normal range from the maximum stress.
The temporal resolution of two LAI datasets is different, causing the Rt to be a multiple of 8 (for GLASS LAI) and 15 (for GIMMS AVHRR LAI), respectively. In addition, the LAI values in the same area among various LAI datasets are not exactly the same. Thus, a min–max normalization was applied to normalize the two annual terrestrial resiliences for comparison and validation, respectively.

2.3.3. Regression Analysis

Linear regression was used to simulate the terrestrial resilience trend for each pixel during the study period, and the least squares method was used to determine the temporal trends:
θ s l o p e = n × ∑ i = 1 n i × R e s i l i e n c e i − ∑ i = 1 n i ∑ i = 1 n R e s i l i e n c e i n × ∑ i = 1 n i 2 − ( ∑ i = 1 n i ) 2
where θ s l o p e is the slope of the terrestrial resilience trend line, n is the number of simulated years, i is the ordinal number of the year, and R e s i l i e n c e i is the terrestrial resilience value of i years. θ s l o p e reflects the trend of the terrestrial resilience during the study period.
Generalized additive regression models (GAM) is a generalized linear model in which the linear predictor depends linearly on unknown smooth functions of some predictor variables, and interest focuses on inference about these smooth functions [56,57]. GAM were originally developed by Trevor Hastie and Robert Tibshirani to blend properties of generalized linear models with additive models [58]. The mathematical description of the GAM can be given as below:
f ( x ) = α +   f 1 ( x 1 ) + f 2 ( x 2 ) + … , f i ( x i ) + ε i
where α is the usual model intercept, the functions f i are different nonlinear functions on variable x i and are modeled by splines, x 1 through x i represent the i values for the predictor variables, and ε i is the random variable. In this study, f ( x ) is the terrestrial ecosystem resilience. The relationship between terrestrial ecosystem resilience and mean annual precipitation (MAP) and mean annual temperature (MAT) was assessed by GAM.

3. Results

3.1. Model Determination and Validation

Terrestrial resilience generated from remote sensing data generally consists of real terrestrial resilience and sensor and data noise [59]. In this study, we applied three methods to reduce the influence of noise on terrestrial resilience measurement, namely, resampling to coarser spatial resolutions, a Savitzky-Golay filter, and β optimization. In order to find the optimal β , drought and fire were selected as the two main disturbances [13]. We selected 52 natural disturbances from 24 points globally in the period of 1982-2011 (Table 2), since the variation ranges of LAI are various within different land-cover types [30]. All points were located in national parks in areas without artificial disturbance, and the 24 points covered the all land-cover types (Figure 3). We observed whether the LAI anomalies and fire or drought were matched by varying the value of β. The optimal value of β would lead to a high proportion of anomaly with disturbance and a low proportion of anomaly without disturbance. Finally, we determined the β for each land-cover type (Table 3).
With the optimal beta ( β ), global resilience was calculated. We took two approaches to validate the result. Firstly, we compared the resilience calculated from GLASS LAI and GIMMS AVHRR LAI 3g (Figure 4). Secondly, the pattern of terrestrial resilience was compared with previous researches. Ecosystem resilience was a relatively loose concept without physical meaning, and previous studies were based on similar but different theoretical hypotheses; therefore, only the pattern of resilience was compared to evaluate global terrestrial ecosystem resilience. Keersmaecker et al. quantified global vegetation resilience using the 1981–2006 GIMMS NDVI dataset and analyzed the average situation of resilience during this period [23]. Similar patterns between our ecosystem resilience and this vegetation resilience were observed (Figure 5). These two datasets showed relatively high resilience in central and western Europe and the northern Great Lakes, and low resilience in western Australia. In addition, Harris et al. used decay times of NDVI trends as a means to characterize the potential resilience of key biomes in southern Africa, and these results showed a pattern similar to our result [24]. Overall, the methods used in this study were reasonable for mapping global terrestrial ecosystem resilience. In addition, our method of determining global terrestrial ecosystem resilience avoided the null value areas that existed in the results of previous studies, and the method improved the temporal resolution of terrestrial ecosystem resilience from a multiyear average to annum.

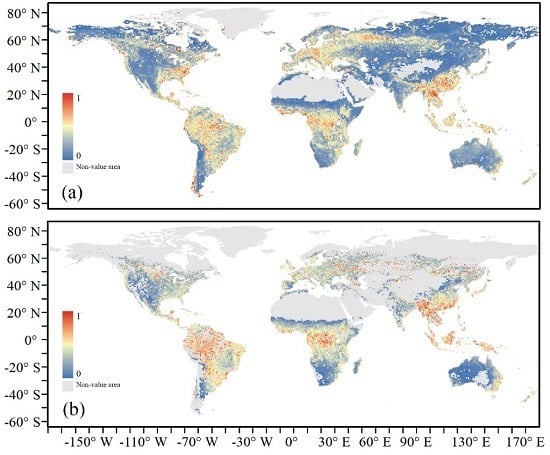
3.2. Spatial Distribution and Temporal Variation of Satellite-Based Terrestrial Resilience

The annual mean terrestrial resilience was divided into five categories globally: low resilience (values of 0.0–0.2), relatively low resilience (0.2–0.4), medium resilience (0.4–0.6), relatively high resilience (0.6–0.8), and high resilience (0.8–1). Half of the resulting pixels showed low and relatively low resilience, and these were located in arid, semiarid, and temperate regions. Regions with medium resilience were found in Europe and tropical regions, more specifically, in the Amazon, central Africa, southeastern Australia, the Caribbean, and Southeast Asia. The pattern of relatively high resilience areas was similar to that of medium resilience areas, but with some subtle differences. For example, the area of relatively high resilience was only one-third as large as the area of medium resilience. Very few groups of terrestrial pixels, except those located in the Amazon and Southeast Asia, showed high resilience according to the multiyear average terrestrial resilience. Consequently, our model did not provide information regarding the resilience of regions consisting mostly of desert or of extremely sparse vegetation.
To compare the terrestrial resilience in different ecosystems, the mean resilience values of different land-cover types were determined (Figure 6). Most forest ecosystems (e.g., broadleaf forest) showed relatively high resilience; however, deciduous needleleaf forest showed relatively low resilience. The gap in resilience between deciduous needleleaf forest and deciduous broadleaf forest was huge; in resilience from GIMMS AVHRR LAI 3g, the resilience of deciduous needleleaf forest was 58% lower than that of deciduous broadleaf forest. The resilience of mixed forest (mean resilience value (from GLASS LAI): 0.52) was slightly lower than that of deciduous broadleaf forest. Among the shrubland, open shrubland had a slightly lower value of resilience than that of close shrubland. Woody savannas and savannas showed large uncertainty on resilience value between the results from GLASS LAI and GIMMS AVHRR LAI 3g. In resilience from GLASS LAI, the resilience value of woody savannas was almost the same as the resilience value of savannas. However, in resilience from GIMMS AVHRR LAI 3g, resilience of savannas was only half of the woody savannas’ resilience. Resilience of grassland and cropland from GLASS LAI were lower than that from GIMMS AVHRR LAI 3g. The resilience value of barren or sparsely vegetated was relatively low.
This study adopted a linear regression model to characterize the variation of global terrestrial resilience. Figure 7 shows the results of the per-pixel linear trend analysis based on the results of two terrestrial resilience datasets. The blue and red colors indicate decreasing and increasing trends, respectively. Resilience decrease mainly appeared in the upper northern latitudes of Europe and, most notably, in Russia, western Finland, Sweden, Romania, eastern France, western Germany, eastern Poland, and Bulgaria. A trend of decline was also found in eastern North America, the Caribbean, southeastern Latin America, and southeastern China—regions that had a rather strong rate of decline of more than 2%/year (terrestrial ecosystem resilience from GLASS LAI). A trend of increase in resilience was found in central India, southern Africa, southern Latin America, and western America—regions that had a rate of increase of more than 2%/year (terrestrial ecosystem resilience from GLASS LAI). A relatively large discrepancy between resilience calculated from GLASS LAI and resilience calculated from GIMMS AVHRR LAI 3g was observed in most of Mexico and northern Australia, where the resilience trend calculated from GLASS LAI was higher than that calculated from GIMMS AVHRR LAI 3g. By comparison, the resilience trend calculated from GLASS LAI and resilience trend calculated from GIMMS AVHRR LAI 3g achieved good consistency at the middle and high latitudes of the Northern and Southern Hemispheres. This is probably because the time period and quality of LAI products were different [32].
In order to compare the variation of terrestrial resilience in different ecosystems, the mean resilience variation of different land-cover types was also calculated using the results from GLASS LAI (Figure 8). Among these ecosystems, resilience in evergreen broadleaf forest, deciduous broadleaf forest, and closed shrubland showed strong fluctuations. The fluctuation of resilience in evergreen broadleaf forest and deciduous needleleaf forest started to weaken in the 21st century, while the fluctuation of resilience in closed shrublands became strong after 2003. Resilience in woody savannas and savannas showed a continuous relatively strong fluctuation in recent decades. Resilience in evergreen needleleaf forest, mixed forest, cropland, and cropland/natural vegetation mosaic showed similar variation patterns, which decreased during the 20th century but started to increase in the 21st century. Resilience in deciduous needleleaf forest, open shrublands, and barren or sparsely vegetated land have remained steady in recent decades. Resilience in grassland and permanent wetlands has exhibited fluctuations, but has not shown obvious changes or trends in recent decades.

3.3. Driving Factors of Satellite-Based Terrestrial Resilience

On a global scale, mean annual precipitation (MAP) had a significant influence on terrestrial resilience. The latter manifests high sensitivity to precipitation for MAP values below 2000 mm. Within that high sensitivity range, we found that terrestrial resilience on a global scale was negative and decreased markedly as MAP dropped below around 500 mm (Figure 9). Above that value, the resilience transitions to positive. The impact of mean annual precipitation on terrestrial resilience remained steady and positive, with mean annual precipitation in the range of 2000 to 3000 mm. We found a huge uncertainty of MAP impact on terrestrial resilience between resilience from GLASS LAI and resilience from GIMMS AVHRR LAI 3g when MAP rose above 3000 mm.
The sensitivity of the terrestrial resilience to mean annual temperature (MAT) was not as strong as to mean annual precipitation (MAP). We found contrasting results of mean annual temperature’s impact on terrestrial resilience between resilience from GLASS LAI and resilience from GIMMS AVHRR LAI 3g when mean annual temperature fell below around -5℃. As mean annual temperature rose, the effect of mean annual temperature on terrestrial resilience started to become vanishingly small. The negative effect of mean annual temperature was observed on terrestrial resilience when mean annual temperature rose up over 25℃ on a global scale.
We found that soil condition exhibits a potential influence on terrestrial resilience. In most udic regimes, terrestrial resilience was high, while terrestrial resilience in most aridic regimes was low (Figure 7 and Figure 10). For permafrost and inter forest regimes, the value of terrestrial resilience had large uncertainty and was not the main focus in this study, since effects of snow on remote sensing data were relatively large.
In addition to the effects of precipitation and temperature, we also found heavy fluctuations of terrestrial resilience were related to disturbance frequency. In recent decades, we observed three heavy fluctuations of natural disturbance frequency in 1989, 1995, and 2001, respectively. In each year of dramatically increasing disturbance frequency, the terrestrial resilience always significantly went down (Figure 11). This relationship from GLASS LAI was more obvious than that from GIMMS AVHRR LAI 3g. Moreover, the correlation between terrestrial resilience and disturbance frequency was undefined when all the data of past three decades were taken into account.

4. Discussion

4.1. Satellite-Based Terrestrial Resilience

Many different theories and potential methodologies of resilience have been developed since the concept of ecosystem resilience was put forward [6,60,61,62,63,64]. Because ecosystem resilience is a broad concept, previous researches has developed many proxy indicators that have been used to present the recovery capability of ecosystem (e.g., resilience, resistance, return interval) [8,13,59,65,66,67,68,69]. Every proxy indicator can reflect the recovery capability of an ecosystem based on different perspectives, although the similar calculation methods of these indicators. In our study, we measured the terrestrial resilience from the site at which the LAI began recovery, indicating that the resilience we measured did not include a capability of resistance. This can explain how deciduous needle-leaf forest had a strong capability to resist natural disasters but, in our study, had a low resilience value.
Despite many theories and methodologies for resilience measurement, long time-series terrestrial ecosystem resilience monitoring has faced several obstacles [70,71]. One of the main obstacles is choosing the appropriate data to represent the state of the ecosystem. The development of remote sensing has provided long time-series data of earth’s surface [31,72]. Among advanced remote sensing products, LAI exhibits very high precision and long time series [25,72,73,74]. Compared with Gross Primary Productivity (GPP) and biomass, LAI is a measurable index in the field, and LAI is directly estimated from remote sensing data using physical models, while GPP and biomass are usually generated from LAI, NDVI or other vegetation indexes and based on statistical modeling [75,76,77]. For this reason, LAI was selected to measure terrestrial resilience in this study.

4.2. Distribution and Variation of Satellite-Based Terrestrial Resilience

In this study, we measured terrestrial resilience in a broad sense to monitor the ability of an ecosystem to return to equilibrium or a steady state following disturbances [29,78]. Previous studies have suggested that terrestrial resilience can be affected by several component, such as climate, hydrology, radiation, and soil condition [9,19,79]. Climate, in particular, has a significant effect on terrestrial resilience [80,81]. Díaz-Delgado found that rainfall had a positive effect on ecosystem resilience response to fire in Mediterranean forest communities [19]. In tropical areas, mean annual precipitation has been found to have a positive effect on vegetation resilience [26,82]. Our study found that mean annual precipitation has more significant impact on terrestrial resilience than mean annual temperature globally in the most recent four decades. Moreover, huge uncertainty of MAP impact on terrestrial resilience between resilience from GLASS LAI and resilience from GIMMS AVHRR LAI 3g was observed when MAP rose above 3000 mm. This is probably due to the influence of clouds and haze in areas with more than 3000 mm MAP, increasing the uncertainty of the LAI datasets [9,26]. Patterns of relationships between terrestrial resilience and climate condition varied among different regions (Figure 12). In deciduous needleleaf forest and savannas, mean annual precipitation did not show a significant impact on terrestrial resilience. The growth of deciduous needleleaf forest is limited by temperature because of its location. For savannas, the increase of precipitation has a contrasted impact on its growth between the wet season and dry season [83,84]. It is worth noting that mean annual precipitation not always has positive effect on all terrestrial ecosystems. Our study found in deciduous broadleaf forest, mixed forest, and closed shrublands that the effect of mean annual precipitation began to convert to negative when mean annual precipitation was excessive.
In our study, no consistent relationships were found between mean annual temperature and terrestrial resilience on a global scale. This was also indirectly confirmed by a previous study that analyzed the relationship between temperature and tropical vegetation resilience [26,85]. Precipitation and temperature both have a huge influence on the state of vegetation, while the impact of mean annual temperature is insignificant on terrestrial resilience that was generated from the vegetation index. There are probably two reasons for this: firstly, the impact of mean annual temperature was offset when it was calculated on a global scale because the impacts of mean annual temperature were contrast among different ecosystems; secondly, the range of temperature variation was narrower and the process of temperature influence slow and long, which is not reflected in statistical results based on nearly four decades of data.
Previous researches have suggested that soil condition has a significant influence on terrestrial resilience. Soil can provide essential nutrition to vegetation for recovery from disturbances [52,86]. In this study, we found that resilience was higher in most udic moisture regimes and lower in most aridic moisture regimes (Figure 10). Moreover, the results of the global mean resilience showed that savannas had low resilience. This agrees with the results of Ponce-Campos, who studied ecosystem resilience under large-scale alteration of the hydroclimatic conditions [79]. They found that savanna water-use efficiency decreased with increasing aridity, which indicates a low resilience of savannas to drought. This could be considered evidence of a relationship between terrestrial resilience and soil moisture regimes, because savanna ecosystems are located largely in aridic moisture regimes at a global scale.
Several studies have found a positive correlation between the time interval between wildfires and terrestrial ecosystem resilience, which indicates that the occurrence of frequent wildfires leads to low resilience [19]. Wildfire can alter ecosystem heterogeneity and also lead to degradation of ecosystem function. Although spatial heterogeneity can enhance the terrestrial resilience of an ecosystem [87], a degraded ecosystem may have lower resilience [80]. For this reason, the relationship between disturbances and resilience remains unclear. In this study, to explore the relationship between disturbance frequency and terrestrial ecosystem resilience, we calculated the number of annual anomalies in recent decades (Figure 11). We observed three dramatic rises of disturbance frequency and three significant drops of resilience correspondingly. The reason for this is probably the dramatically increasing frequency of disturbance changes soil characteristics, reducing nutrient availability, and increasing soil susceptibility, which might prolong the time required for recovery from a disturbance. Furthermore, the short-term spatial legacies of disturbance can persist for years to decades [2]. High-frequency disturbances have an interaction effect and create a novel disturbance with potential impacts on the ecosystem [88]. Furthermore, the correlation between terrestrial resilience and disturbance frequency was undefined when all the data of past three decades were taken into account. This is probably because the impacts of disturbance frequency’s slight fluctuation on terrestrial resilience can be offset by other environmental factors.
For the resilience variation among various ecosystems, we found the fluctuation of resilience in evergreen broadleaf forest and deciduous needleleaf forest have started to weaken in 21st century, while the fluctuation of resilience in closed shrublands became strong after 2003. Resilience in evergreen needleleaf forest, mixed forest, cropland, and cropland/natural vegetation mosaic decreased in the 20st century, then started to increase in the 21st century. Obvious change was not found from precipitation and soil conditions in these ecosystems [89]. This is probably because of the effects of El Niño, which was strongly monitored in 1997 and 1998 and led to disturbance frequency change [90]. Other causes need to be analyzed by future works.
In our study, we did not measure terrestrial resilience in certain highly managed ecosystems such as cropland/natural vegetation mosaic or urban and built-up areas, because they are not natural ecosystems. They might be well organized and highly productive, but they are subject to collapse without management due to their lack of a capacity to recover from disturbance [29,91].

4.3. Limitations and Recommendations for Future Research

Although remote sensing has advantages for large-scale and long-term environmental monitoring and leads to outstanding global terrestrial resilience measurement performance compared with field studies, it has three known limitations. Firstly, imperfect removal of cloud and noise in remote sensing products can affect terrestrial ecosystem resilience measurement, although these products promote high accuracy [26]. Secondly, remote sensing products cover relatively limited aspects, focusing mainly on vegetation, compared with the complexity of ecosystems [92]. Finally, the limitation of the number of field studies constrains extensive validation. In addition, a lack of uniformity of terrestrial resilience leads to a low availability of extant field data.
To make large-scale resilience monitoring more applicable globally, it is urgent to collect more resilience-related information for ecosystem resilience measurement. Most previous studies have used mainly temporal indicators to measure ecosystem resilience (e.g., temporal autocorrelation, temporal variance), but recent evidence has shown that spatial pattern dynamics could lead the change of resilience [8]. Several spatial indicators have been developed, and this facilitates more comprehensive methods of resilience measurement based on multi-indicators. Future research will consider both temporal information and spatial information when developing resilience indexes to improve the accuracy of global resilience measurement.

5. Conclusions

Terrestrial ecosystem resilience is an important component of ecosystem health and ecosystem function. The identification of large-scale metrics to quantify terrestrial ecosystem resilience and its dynamics remains a vital strategy for global ecosystem assessment. In this study, we mapped global terrestrial ecosystem resilience based on the long time-series GLASS LAI and GIMMS AVHRR LAI 3g products. The result showed that, globally, evergreen broadleaf forest exhibited the highest resilience and deciduous needleleaf forest exhibited the lowest resilience. On a global scale, the increase of mean annual precipitation has a positive effect on terrestrial resilience enhancement, while we found no consistent relationships between mean annual temperature and terrestrial resilience. For terrestrial resilience dynamics, we observed three dramatic raises of disturbance frequency in 1989, 1995, and 2001, respectively, and three significant drops of resilience correspondingly. On a regional scale, the distribution and dynamic of resilience have also been analyzed based on different land cover. Our study avoided the problems of some areas having null values encountered in previous studies, and this method improved the time scale of terrestrial ecosystem resilience to the interannual scale. This study demonstrated that satellites are effective for monitoring terrestrial resilience for global ecosystem assessment. With the availability of longer records of remotely sensed products, future research will consider both temporal information and spatial information when developing resilience indexes, which will improve the accuracy of resilience measurement.

Author Contributions

J.W. and S.L. conceived and designed the experiments; J.W. performed the experiments; J.W. analyzed the data; J.W. and S.L. contributed to the analysis of the results; all of the aforementioned contributed towards writing the manuscript. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the National Key Research and Development Program of China (2016YFA0600103) and the Natural Science Fund of China (No. 41331173).

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Tittensor, D.P.; Walpole, M.; Hill, S.L.; Boyce, D.G.; Britten, G.L.; Burgess, N.D.; Butchart, S.H.; Leadley, P.W.; Regan, E.C.; Alkemade, R. A mid-term analysis of progress toward international biodiversity targets. Science 2014, 346, 241–244. [Google Scholar] [CrossRef] [PubMed]
  2. Hudson, L.N.; Newbold, T.; Contu, S.; Hill, S.L.L.; Lysenko, I.; De Palma, A.; Phillips, H.R.P.; Senior, R.A.; Bennett, D.J.; Booth, H.; et al. The predicts database: A global database of how local terrestrial biodiversity responds to human impacts. Ecol. Evol. 2014, 4, 4701–4735. [Google Scholar] [CrossRef] [PubMed]
  3. U.S. Environmental Protection Agency (EPA). Climate Change Indicators in the United States; U.S. Environmental Protection Agency (EPA): Washington, DC, USA, 2010. [Google Scholar]
  4. Nemani, R.R.; Keeling, C.D.; Hashimoto, H.; Jolly, W.M.; Piper, S.C.; Tucker, C.J.; Myneni, R.B.; Running, S.W. Climate-driven increases in global terrestrial net primary production from 1982 to 1999. Science 2003, 300, 1560–1563. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  5. Zhao, M.; Running, S.W. Drought-induced reduction in global terrestrial net primary production from 2000 through 2009. Science 2010, 329, 940–943. [Google Scholar] [CrossRef] [Green Version]
  6. Holling, C.S. Resilience and stability of ecological systems. Ann. Rev. Ecol. Syst. 1973, 4, 1–23. [Google Scholar] [CrossRef] [Green Version]
  7. Pimm, S.L. The complexity and stability of ecosystems. Nature 1984, 307, 321–326. [Google Scholar] [CrossRef]
  8. Scheffer, M.; Carpenter, S.R.; Dakos, V.; Van Nes, E.H. Generic indicators of ecological resilience: Inferring the chance of a critical transition. Ann. Rev. Ecol. Evol. Syst. 2015, 46, 145–167. [Google Scholar] [CrossRef]
  9. Hirota, M.; Holmgren, M.; Van Nes, E.H.; Scheffer, M. Global resilience of tropical forest and savanna to critical transitions. Science 2011, 334, 232–235. [Google Scholar] [CrossRef] [Green Version]
  10. Walker, B.H.; Abel, N.; Anderies, J.M.; Ryan, P. Resilience, adaptability, and transformability in the goulburn-broken catchment, australia. Ecol. Soc. 2009, 14, 12. [Google Scholar] [CrossRef]
  11. Westman, W.E.; O’Leary, J.F. Measures of resilience: The response of coastal sage scrub to fire. Vegetatio 1986, 65, 179–189. [Google Scholar] [CrossRef]
  12. Wang, R.; Dearing, J.A.; Langdon, P.G.; Zhang, E.; Yang, X.; Dakos, V.; Scheffer, M. Flickering gives early warning signals of a critical transition to a eutrophic lake state. Nature 2012, 492, 419. [Google Scholar] [CrossRef] [PubMed]
  13. MacGillivray, C.; Grime, J.; Team, T.I.S.P. Testing predictions of the resistance and resilience of vegetation subjected to extreme events. Funct. Ecol. 1995, 9, 640–649. [Google Scholar] [CrossRef]
  14. Wu, J.; Liang, S. Developing an integrated remote sensing based biodiversity index for predicting animal species richness. Remote Sens. 2018, 10, 739. [Google Scholar] [CrossRef] [Green Version]
  15. Gong, P.; Wang, J.; Yu, L.; Zhao, Y.; Zhao, Y.; Liang, L.; Niu, Z.; Huang, X.; Fu, H.; Liu, S. Finer resolution observation and monitoring of global land cover: First mapping results with landsat tm and etm+ data. Int. J. Remote Sens. 2013, 34, 2607–2654. [Google Scholar] [CrossRef] [Green Version]
  16. Huete, A. Ecology: Vegetation’s responses to climate variability. Nature 2016, 531, 181–182. [Google Scholar] [CrossRef] [PubMed]
  17. Bisson, M.; Fornaciai, A.; Coli, A.; Mazzarini, F.; Pareschi, M.T. The vegetation resilience after fire (vraf) index: Development, implementation and an illustration from central italy. Int. J. Appl. Earth Observ. Geoinform. 2008, 10, 312–329. [Google Scholar] [CrossRef]
  18. Mauro, B.D.; Fava, F.; Busetto, L.; Crosta, G.F.; Colombo, R. Post-fire resilience in the alpine region estimated from modis satellite multispectral data. Int. J. Appl. Earth Observ. Geoinform. 2014, 32, 163–172. [Google Scholar] [CrossRef]
  19. Díaz-Delgado, R.; Lloret, F.; Pons, X.; Terradas, J. Satellite evidence of decreasing resilience in mediterranean plant communities after recurrent wildfires. Ecology 2002, 83, 2293–2303. [Google Scholar] [CrossRef] [Green Version]
  20. Schwalm, C.R.; Anderegg, W.R.L.; Michalak, A.M.; Fisher, J.B.; Biondi, F.; Koch, G.; Litvak, M.; Ogle, K.; Shaw, J.D.; Wolf, A.; et al. Global patterns of drought recovery. Nature 2017, 548, 202–205. [Google Scholar] [CrossRef]
  21. Van Nes, E.H.; Holmgren, M.; Hirota, M.; Scheffer, M. Response to comment on “global resilience of tropical forest and savanna to critical transitions”. Science 2012, 336, 541–541. [Google Scholar] [CrossRef] [Green Version]
  22. Ratajczak, Z.; Nippert, J.B. Comment on “global resilience of tropical forest and savanna to critical transitions”. Science 2012, 336, 541–541. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  23. De Keersmaecker, W.; Lhermitte, S.; Tits, L.; Honnay, O.; Somers, B.; Coppin, P. A model quantifying global vegetation resistance and resilience to short-term climate anomalies and their relationship with vegetation cover. Global Ecol. Biogeogr. 2015, 24, 539–548. [Google Scholar] [CrossRef]
  24. Harris, A.; Carr, A.; Dash, J. Remote sensing of vegetation cover dynamics and resilience across southern africa. Int. J. Appl. Earth Observ. Geoinform. 2014, 28, 131–139. [Google Scholar] [CrossRef]
  25. Seddon, A.W.; Macias-Fauria, M.; Long, P.R.; Benz, D.; Willis, K.J. Sensitivity of global terrestrial ecosystems to climate variability. Nature 2016, 531, 229–232. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  26. Verbesselt, J.; Umlauf, N.; Hirota, M.; Holmgren, M.; Van Nes, E.H.; Herold, M.; Zeileis, A.; Scheffer, M. Remotely sensed resilience of tropical forests. Nat. Clim. Change 2016, 6, 1028–1031. [Google Scholar] [CrossRef]
  27. Holling, C.S. The resilience of terrestrial ecosystems: Local surprise and global change. Sustain. Dev. Biosph. 1986, 14, 292–317. [Google Scholar]
  28. Pimm, S.L. Complexity and stability: Another look at macarthur’s original hypothesis. Oikos 1979, 351–357. [Google Scholar] [CrossRef]
  29. Costanza, R. Ecosystem health and ecological engineering. Ecol. Eng. 2012, 45, 24–29. [Google Scholar] [CrossRef] [Green Version]
  30. Xiao, Z.; Liang, S.; Wang, J.; Xiang, Y.; Zhao, X.; Song, J. Long-time-series global land surface satellite leaf area index product derived from modis and avhrr surface reflectance. IEEE Trans. Geosci. Remote Sens. 2016, 54, 5301–5318. [Google Scholar] [CrossRef]
  31. Liang, S.; Zhao, X.; Liu, S.; Yuan, W.; Cheng, X.; Xiao, Z.; Zhang, X.; Liu, Q.; Cheng, J.; Tang, H. A long-term global land surface satellite (glass) data-set for environmental studies. Int. J. Digit. Earth 2013, 6, 5–33. [Google Scholar] [CrossRef]
  32. Xiao, Z.; Liang, S.; Jiang, B. Evaluation of four long time-series global leaf area index products. Agricult. Forest Meteorol. 2017, 246, 218–230. [Google Scholar] [CrossRef]
  33. Zhu, Z.; Piao, S.; Myneni, R.B.; Huang, M.; Zeng, Z.; Canadell, J.G.; Ciais, P.; Sitch, S.; Friedlingstein, P.; Arneth, A.; et al. Greening of the earth and its drivers. Nat. Clim. Change 2016, 6, 791. [Google Scholar] [CrossRef]
  34. Liang, S.; Yi, Q.; Liu, J. Vegetation dynamics and responses to recent climate change in xinjiang using leaf area index as an indicator. Ecol. Indic. 2015, 58, 64–76. [Google Scholar]
  35. Kim, K.; Wang, M.-c.; Ranjitkar, S.; Liu, S.-h.; Xu, J.-c.; Zomer, R.J. Using leaf area index (lai) to assess vegetation response to drought in yunnan province of china. J. Mount. Sci. 2017, 14, 1863–1872. [Google Scholar] [CrossRef]
  36. Zhu, Z.; Bi, J.; Pan, Y.; Ganguly, S.; Anav, A.; Xu, L.; Samanta, A.; Piao, S.; Nemani, R.R.; Myneni, R.B. Global data sets of vegetation leaf area index (lai) 3g and fraction of photosynthetically active radiation (fpar) 3g derived from global inventory modeling and mapping studies (gimms) normalized difference vegetation index (ndvi3g) for the period 1981 to 2011. Remote Sens. 2013, 5, 927–948. [Google Scholar]
  37. Page, Y.L.; Pereira, J.; Trigo, R.; Camara, C.d.; Oom, D.; Mota, B. Global fire activity patterns (1996–2006) and climatic influence: An analysis using the world fire atlas. Atmosph. Chem. Phys. 2008, 8, 1911–1924. [Google Scholar] [CrossRef] [Green Version]
  38. Arino, O.; Casadio, S.; Serpe, D. Global night-time fire season timing and fire count trends using the atsr instrument series. Remote Sens. Environ. 2012, 116, 226–238. [Google Scholar] [CrossRef]
  39. Friedl, M.; Sulla-Menashe, D. MCD12Q1 MODIS/Terra+Aqua Land Cover Type Yearly L3 Global 500m SIN Grid V006. 2019, distributed by NASA EOSDIS Land Processes DAAC. Available online: https://doi.org/10.5067/MODIS/MCD12Q1.006 (accessed on 4 February 2020).
  40. Friedl, M.A.; McIver, D.K.; Hodges, J.C.; Zhang, X.; Muchoney, D.; Strahler, A.H.; Woodcock, C.E.; Gopal, S.; Schneider, A.; Cooper, A. Global land cover mapping from modis: Algorithms and early results. Remote Sens. Environ. 2002, 83, 287–302. [Google Scholar] [CrossRef]
  41. Wu, D.; Zhao, X.; Liang, S.; Zhou, T.; Huang, K.; Tang, B.; Zhao, W. Time-lag effects of global vegetation responses to climate change. Global Change Biol. 2015, 21, 3520–3531. [Google Scholar] [CrossRef] [PubMed]
  42. Schrier, G.; Barichivich, J.; Briffa, K.; Jones, P. A scpdsi-based global data set of dry and wet spells for 1901–2009. J. Geophys. Res. Atmosph. 2013, 118, 4025–4048. [Google Scholar] [CrossRef]
  43. Wells, N.; Goddard, S.; Hayes, M.J. A self-calibrating palmer drought severity index. J. Clim. 2004, 17, 2335–2351. [Google Scholar] [CrossRef]
  44. Dai, A. Increasing drought under global warming in observations and models. Nat. Clim. Change 2013, 3, 52–58. [Google Scholar] [CrossRef]
  45. Harris, I.; Jones, P.; Osborn, T.; Lister, D. Updated high-resolution grids of monthly climatic observations–the cru ts3. 10 dataset. Int. J. Climatol. 2014, 34, 623–642. [Google Scholar] [CrossRef] [Green Version]
  46. New, M.; Hulme, M.; Jones, P. Representing twentieth-century space–time climate variability. Part ii: Development of 1901–96 monthly grids of terrestrial surface climate. J. Clim. 2000, 13, 2217–2238. [Google Scholar] [CrossRef]
  47. Mitchell, T.D.; Jones, P.D. An improved method of constructing a database of monthly climate observations and associated high-resolution grids. Int. J. Climatol. 2005, 25, 693–712. [Google Scholar] [CrossRef]
  48. Wang, X.; Piao, S.; Ciais, P.; Li, J.; Friedlingstein, P.; Koven, C.; Chen, A. Spring temperature change and its implication in the change of vegetation growth in north america from 1982 to 2006. Proc. Natl. Acad. Sci. USA 2011, 108, 1240–1245. [Google Scholar] [CrossRef] [Green Version]
  49. Jones, P.; Lister, D.; Osborn, T.; Harpham, C.; Salmon, M.; Morice, C. Hemispheric and large-scale land-surface air temperature variations: An extensive revision and an update to 2010. J. Geophys. Res. Atmosph. 2012, 117. [Google Scholar] [CrossRef] [Green Version]
  50. Jong, R.; Schaepman, M.E.; Furrer, R.; Bruin, S.; Verburg, P.H. Spatial relationship between climatologies and changes in global vegetation activity. Glob. Change Biol. 2013, 19, 1953–1964. [Google Scholar] [CrossRef]
  51. Peng, S.; Piao, S.; Ciais, P.; Myneni, R.B.; Chen, A.; Chevallier, F.; Dolman, A.J.; Janssens, I.A.; Penuelas, J.; Zhang, G. Asymmetric effects of daytime and night-time warming on northern hemisphere vegetation. Nature 2013, 501, 88. [Google Scholar] [CrossRef]
  52. Beinroth, F.H.; Eswaran, H.; Reich, P.F. Global assessment of land quality. Sustain. Global Farm 2001, 569–574. Available online: https://topsoil.nserl.purdue.edu/nserlweb-old/isco99/pdf/ISCOdisc/SustainingTheGlobalFarm/P233-Beinroth.pdf (accessed on 30 January 2020).
  53. Hild, S.; Chelkowski, S.; Freise, A. Pushing towards the et sensitivity using ‘conventional’ technology. arXiv 2008, preprint. arXiv:0810.0604. [Google Scholar]
  54. Mageau, M.T.; Costanza, R.; Ulanowicz, R.E. The development and initial testing of a quantitative assessment of ecosystem health. Health 1995, 1, 201–213. [Google Scholar]
  55. Mageau, M.T. Development and testing of a quantitative assessment of ecosystem health. Ecosyst. Health 1998, 1, 201–213. [Google Scholar]
  56. Wood, S.N. Generalized Additive Models: An Introduction with r; Chapman & Hall/CRC: Boca Raton, FL, USA, 2006. [Google Scholar]
  57. Fahrmeir, L.; Kneib, T.; Lang, S.; Marx, B. Regression: Models, Methods and Applications; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
  58. Hastie, T.J.; Tibshirani, R.J. Generalized Additive Models; Chapman & Hall/CRC: Boca Raton, FL, USA, 1990. [Google Scholar]
  59. Washington-Allen, R.A.; Ramsey, R.; West, N.E.; Norton, B.E. Quantification of the ecological resilience of drylands using digital remote sensing. Ecol. Soc. 2008, 13, 33. [Google Scholar] [CrossRef] [Green Version]
  60. Pimm, S.L. The Balance of Nature? Ecological Issues in the Conservation of Species and Communities; University of Chicago Press: Chicago, IL, USA, 1991. [Google Scholar]
  61. Peterson, G.; Allen, C.R.; Holling, C.S. Ecological resilience, biodiversity, and scale. Ecosystems 1998, 1, 6–18. [Google Scholar] [CrossRef]
  62. Scheffer, M.; Carpenter, S.; Foley, J.A.; Folke, C.; Walker, B. Catastrophic shifts in ecosystems. Nature 2001, 413, 591–596. [Google Scholar] [CrossRef]
  63. Folke, C.; Carpenter, S.; Walker, B.; Scheffer, M.; Elmqvist, T.; Gunderson, L.; Holling, C. Regime shifts, resilience, and biodiversity in ecosystem management. Ann. Rev. Ecol. Evol. Syst. 2004, 35, 557–581. [Google Scholar] [CrossRef] [Green Version]
  64. Lloret, F.; Keeling, E.G.; Sala, A. Components of tree resilience: Effects of successive low-growth episodes in old ponderosa pine forests. Oikos 2011, 120, 1909–1920. [Google Scholar] [CrossRef]
  65. Cumming, G.S. Spatial resilience: Integrating landscape ecology, resilience, and sustainability. Landsc. Ecol. 2011, 26, 899–909. [Google Scholar] [CrossRef]
  66. Turner, M.G. Disturbance and landscape dynamics in a changing world. Ecology 2010, 91, 2833–2849. [Google Scholar] [CrossRef] [Green Version]
  67. Lanfredi, M.; Simoniello, T.; Macchiato, M. Temporal persistence in vegetation cover changes observed from satellite: Development of an estimation procedure in the test site of the mediterranean italy. Remote Sens. Environ. 2004, 93, 565–576. [Google Scholar]
  68. Baho, D.; Allen, C.; Garmestani, A.; Fried-Petersen, H.; Renes, S.; Gunderson, L.; Angeler, D. A quantitative framework for assessing ecological resilience. Ecol. Soc. 2017, 22. [Google Scholar] [CrossRef] [Green Version]
  69. Standish, R.J.; Hobbs, R.J.; Mayfield, M.M.; Bestelmeyer, B.T.; Suding, K.N.; Battaglia, L.L.; Eviner, V.; Hawkes, C.V.; Temperton, V.M.; Cramer, V.A. Resilience in ecology: Abstraction, distraction, or where the action is? Biol. Conserv. 2014, 177, 43–51. [Google Scholar] [CrossRef] [Green Version]
  70. Deffuant, G.; Gilbert, N. Viability and Resilience of Complex Systems: Concepts, Methods and Case Studies from Ecology and Society; Springer Science & Business Media: Berlin, Germany, 2011. [Google Scholar]
  71. Cantarello, E.; Newton, A.C.; Martin, P.A.; Evans, P.M.; Gosal, A.; Lucash, M.S. Quantifying resilience of multiple ecosystem services and biodiversity in a temperate forest landscape. Ecol. Evolut. 2017, 7, 9661–9675. [Google Scholar] [CrossRef] [Green Version]
  72. Liang, S.; Li, X.; Wang, J. Advanced Remote Sensing: Terrestrial Information Extraction and Applications; Academic Press: Cambridge, MA, USA, 2012. [Google Scholar]
  73. Keersmaecker, W.; Lhermitte, S.; Honnay, O.; Farifteh, J.; Somers, B.; Coppin, P. How to measure ecosystem stability? An evaluation of the reliability of stability metrics based on remote sensing time series across the major global ecosystems. Glob. Change Biol. 2014, 20, 2149–2161. [Google Scholar] [CrossRef] [PubMed]
  74. Rammig, A.; Mahecha, M.D. Ecology: Ecosystem responses to climate extremes. Nature 2015, 527, 315–316. [Google Scholar] [CrossRef] [PubMed]
  75. Yuan, W.; Liu, S.; Yu, G.; Bonnefond, J.; Chen, J.; Davis, K.J.; Desai, A.R.; Goldstein, A.H.; Gianelle, D.; Rossi, F. Global estimates of evapotranspiration and gross primary production based on modis and global meteorology data. Remote Sens. Environ. 2010, 114, 1416–1431. [Google Scholar] [CrossRef] [Green Version]
  76. Zhang, Y.; Liang, S.; Sun, G. Forest biomass mapping of northeastern china using glas and modis data. Ieee J.-Stars 2014, 7, 140–152. [Google Scholar]
  77. Zhao, M.; Heinsch, F.A.; Nemani, R.R.; Running, S.W. Improvements of the modis terrestrial gross and net primary production global data set. Remote Sens. Environ. 2005, 95, 164–176. [Google Scholar]
  78. Gunderson, L.H. Ecological resilience--in theory and application. Ann. Rev. Ecol. Syst. 2000, 31, 425–439. [Google Scholar] [CrossRef] [Green Version]
  79. Ponce-Campos, G.E.; Moran, M.S.; Huete, A.; Zhang, Y.; Bresloff, C.; Huxman, T.E.; Eamus, D.; Bosch, D.D.; Buda, A.R.; Gunter, S.A. Ecosystem resilience despite large-scale altered hydroclimatic conditions. Nature 2013, 494, 349–352. [Google Scholar] [CrossRef] [PubMed]
  80. Côté, I.M.; Darling, E.S. Rethinking ecosystem resilience in the face of climate change. PLoS Biol. 2010, 8, e1000438. [Google Scholar] [CrossRef] [PubMed]
  81. McDowell, N.G.; Coops, N.C.; Beck, P.S.; Chambers, J.Q.; Gangodagamage, C.; Hicke, J.A.; Huang, C.-y.; Kennedy, R.; Krofcheck, D.J.; Litvak, M. Global satellite monitoring of climate-induced vegetation disturbances. Trends Plant Sci. 2015, 20, 114–123. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  82. Saatchi, S.; Asefi-Najafabady, S.; Malhi, Y.; Aragão, L.E.; Anderson, L.O.; Myneni, R.B.; Nemani, R. Persistent effects of a severe drought on amazonian forest canopy. Proc. Natl. Acad. Sci. USA 2013, 110, 565–570. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  83. Taylor, J.A.; Tulloch, D. Rainfall in the wet-dry tropics: Extreme events at darwin and similarities between years during the period 1870–1983 inclusive. Aust. Ecol. 1985, 10, 281–295. [Google Scholar] [CrossRef]
  84. O’Grady, A.; Eamus, D.; Hutley, L. Transpiration increases during the dry season: Patterns of tree water use in eucalypt open-forests of northern australia. Tree Physiol. 1999, 19, 591–597. [Google Scholar] [CrossRef]
  85. Dakos, V.; Van Nes, E.H.; D’Odorico, P.; Scheffer, M. Robustness of variance and autocorrelation as indicators of critical slowing down. Ecology 2012, 93, 264–271. [Google Scholar] [CrossRef] [Green Version]
  86. DeAngelis, D. Dynamics of Nutrient Cycling and Food Webs; Springer Science & Business Media: Berlin, Germany, 2012; Volume 9. [Google Scholar]
  87. Oliver, T.H.; Heard, M.S.; Isaac, N.J.B.; Roy, D.B.; Procter, D.A.; Eigenbrod, F.; Freckleton, R.P.; Hector, A.L.; Orme, C.D.L.; Petchey, O.L. Biodiversity and resilience of ecosystem functions. Trends Ecol. Evolut. 2015, 30, 673. [Google Scholar] [CrossRef] [Green Version]
  88. Buma, B.; Wessman, C.A. Disturbance interactions can impact resilience mechanisms of forests. Ecosphere 2011, 2, 1–13. [Google Scholar] [CrossRef]
  89. Adler, R.F.; Gu, G.; Sapiano, M.R.P.; Wang, J.; Huffman, G.J. Global precipitation: Means, variations and trends during the satellite era (1979–2014). Surveys Geophys. 2017, 38, 679–699. [Google Scholar] [CrossRef] [Green Version]
  90. Gu, G.; Adler, R.F. Precipitation and temperature variations on the interannual time scale: Assessing the impact of enso and volcanic eruptions. J. Clim. 2011, 24, 2258–2270. [Google Scholar] [CrossRef] [Green Version]
  91. Costanza, R.; Mageau, M. What is a healthy ecosystem? Aquat. Ecol. 1999, 33, 105–115. [Google Scholar] [CrossRef]
  92. Turner, W. Sensing biodiversity. Science 2014, 346, 301–302. [Google Scholar] [CrossRef] [PubMed]
Remotesensing 12 00595 g001 550
Figure 1. Simplified process of ecosystem anomaly. The two components of terrestrial resilience can be extracted: Rt is the recovery time and Ms is the maximum stress.
Figure 1. Simplified process of ecosystem anomaly. The two components of terrestrial resilience can be extracted: Rt is the recovery time and Ms is the maximum stress.
Remotesensing 12 00595 g001
Remotesensing 12 00595 g002 550
Figure 2. The rule of annual terrestrial resilience calculation. The red dot is the start point of recovery and the red line is the recovery time. The red “Resilience” is the resilience value calculated from LAI anomaly.
Figure 2. The rule of annual terrestrial resilience calculation. The red dot is the start point of recovery and the red line is the recovery time. The red “Resilience” is the resilience value calculated from LAI anomaly.
Remotesensing 12 00595 g002
Remotesensing 12 00595 g003 550
Figure 3. Locations of reference sites.
Figure 3. Locations of reference sites.
Remotesensing 12 00595 g003
Remotesensing 12 00595 g004 550
Figure 4. Terrestrial ecosystem resilience (from GLASS LAI) vs terrestrial ecosystem resilience (from GIMMS AVHRR LAI 3g).
Figure 4. Terrestrial ecosystem resilience (from GLASS LAI) vs terrestrial ecosystem resilience (from GIMMS AVHRR LAI 3g).
Remotesensing 12 00595 g004
Remotesensing 12 00595 g005 550
Figure 5. Distribution of terrestrial ecosystem resilience. (a) terrestrial resilience from GLASS LAI, (b) terrestrial resilience from GIMMS AVHRR LAI 3g, (c) global vegetation resilience from Keersmaecker et al., and (d) Southern Africa ecosystem resilience from Harris et al.
Figure 5. Distribution of terrestrial ecosystem resilience. (a) terrestrial resilience from GLASS LAI, (b) terrestrial resilience from GIMMS AVHRR LAI 3g, (c) global vegetation resilience from Keersmaecker et al., and (d) Southern Africa ecosystem resilience from Harris et al.
Remotesensing 12 00595 g005
Remotesensing 12 00595 g006 550
Figure 6. Terrestrial resilience in different land-cover types. The bars represents the mean terrestrial resilience in different land cover types.
Figure 6. Terrestrial resilience in different land-cover types. The bars represents the mean terrestrial resilience in different land cover types.
Remotesensing 12 00595 g006
Remotesensing 12 00595 g007 550
Figure 7. Change rate of terrestrial ecosystem resilience. (a) Terrestrial resilience from GLASS LAI, (b) terrestrial resilience from GIMMS AVHRR LAI 3g. Non-significant pixels have been masked.
Figure 7. Change rate of terrestrial ecosystem resilience. (a) Terrestrial resilience from GLASS LAI, (b) terrestrial resilience from GIMMS AVHRR LAI 3g. Non-significant pixels have been masked.
Remotesensing 12 00595 g007
Remotesensing 12 00595 g008 550
Figure 8. Annual variations of terrestrial resilience in different land-cover types.
Figure 8. Annual variations of terrestrial resilience in different land-cover types.
Remotesensing 12 00595 g008
Remotesensing 12 00595 g009 550
Figure 9. Resilience as a function of mean annual precipitation (MAP) and mean annual temperature (MAT) on a global scale. The black solid lines represent the mean curve from an ensemble of six curves. The dashed lines highlight the range of the individual ensemble members. The distributions of the available MAP and MAT observations are indicated by the density of the vertical lines above the x-axis.
Figure 9. Resilience as a function of mean annual precipitation (MAP) and mean annual temperature (MAT) on a global scale. The black solid lines represent the mean curve from an ensemble of six curves. The dashed lines highlight the range of the individual ensemble members. The distributions of the available MAP and MAT observations are indicated by the density of the vertical lines above the x-axis.
Remotesensing 12 00595 g009
Remotesensing 12 00595 g010 550
Figure 10. Global soil moisture regime map.
Figure 10. Global soil moisture regime map.
Remotesensing 12 00595 g010
Remotesensing 12 00595 g011 550
Figure 11. Annual variations of global terrestrial resilience and disturbance. The annual terrestrial ecosystem resilience was calculated by averaging the values of resilience detected each year.
Figure 11. Annual variations of global terrestrial resilience and disturbance. The annual terrestrial ecosystem resilience was calculated by averaging the values of resilience detected each year.
Remotesensing 12 00595 g011
Remotesensing 12 00595 g012 550
Figure 12. Resilience as a function of MAP and MAT on a global scale in different land-cover types. The black solid lines represent the mean curve from an ensemble of six curves. The dashed lines highlight the range of the individual ensemble members. The distributions of the available MAP and MAT observations are indicated by the density of the vertical lines above the x-axis.
Figure 12. Resilience as a function of MAP and MAT on a global scale in different land-cover types. The black solid lines represent the mean curve from an ensemble of six curves. The dashed lines highlight the range of the individual ensemble members. The distributions of the available MAP and MAT observations are indicated by the density of the vertical lines above the x-axis.
Remotesensing 12 00595 g012
Table
Table 1. Overview of data properties.
Table 1. Overview of data properties.
IndexSourceBase PeriodSpatial ResolutionTemporal Resolution
Leaf Area IndexGLASS AVHRR LAI1982–20160.05°8 days
GIMMS AVHRR LAI 3g1982–20111/12°15 days
FireATSR World Fire Atlas2000–20090.05°monthly
Droughtsc-PDSI2000–20090.5°monthly
Land CoverMODIS MCD12Q12001-20121/12°yearly
PrecipitationCRU TS4.01 Precipitation1982–20110.5°monthly
TemperatureCRU TS4.01 Mean Temperature1982–20110.5°monthly
Soil moistureUSDA-NRCS19971/30°yearly
Table
Table 2. The reference points.
Table 2. The reference points.
NameCoordinateDisturbance TimeDisturbance Type
Yellowstone national park44°45′N; 110°15′W1988, 1994, 2008Drought
IIha do bananal9°45′S; 49°45′W1994, 1995 (fire)Drought, Fire
Abumonbazi reserve3°15′N; 21°45′E1986, 1994Drought
Three river headwater33°45′N; 94°15′E1995, 2007Drought
Khan khentii national park46°45′N; 119°45′E1992, 1993, 2007Drought
Southern tanami reserve21°15′S; 129°45′E1988, 2005, 1995Drought
Indigenous protected area0°45′S; 65°15′W1982, 1991, 2005Drought
Kenozersky national park61°45′N; 38°15′E1992, 2008Drought
Wabakimi provincial park50°45′N; 89°45′W1999, 2004, 2009Drought
defensores del chaco national park20°15′S; 60°15′W1993, 2007,Drought
Turgaiskiy national park48°45′N; 61°45′E1994, 2001, 2006, 2008Drought
Quetico provinvial park48°15′N; 91°15′W1988, 2007Drought
Baishuijiang nature reserve32°45′N; 104°45′E1989, 2006Drought
Gemsbok national park24°45′S; 21°15′E1985, 2007Drought
Upenba national park8°45′S; 26°45′E1994, 1999Drought
Mavinga national park16°15′S; 21°15′E2005Drought
Witjira national park26°15′S; 135°45′E1994Drought
Lorentz national park4°15′S; 137°45′E2003Drought
Angoran protected area36°45′N; 47°30′E1997, 1999, 2008Drought
Lower rio grande valley26°30′N; 98°45′W2011Drought
Floresta national park2°45′N; 61°45′W1997, 2003Fire
Laguna del Tigre national17°45′N; 90°45′W1998, 2003, 2005Fire
Okefenokee national wildlife refuge30°15′N; 82°15′W2007Fire
Machaquila national wildlife refuge16°15′N; 89°45′W1998, 2000Fire
Table
Table 3. Beta coefficient in resilience calculation.
Table 3. Beta coefficient in resilience calculation.
Land-Cover TypeBeta Coefficient (for GLASS LAI)Beta Coefficient (for GIMMS LAI 3g)
Barren or sparsely vegetated0.40.35
Cropland and natural vegetation0.50.4
Cropland0.450.4
Permanent wetlands0.450.4
Grassland0.350.3
Savannas0.350.3
Woody savannas0.350.3
Open shrublands0.550.5
Closed shrubland0.550.5
Mixed forest0.60.55
Deciduous broadleaf forest0.60.55
Deciduous needleleaf forest0.60.55
Evergreen broadleaf forest0.60.55
Evergreen needleleaf forest0.60.55

Share and Cite

MDPI and ACS Style

Wu, J.; Liang, S. Assessing Terrestrial Ecosystem Resilience using Satellite Leaf Area Index. Remote Sens. 2020, 12, 595. https://doi.org/10.3390/rs12040595

AMA Style

Wu J, Liang S. Assessing Terrestrial Ecosystem Resilience using Satellite Leaf Area Index. Remote Sensing. 2020; 12(4):595. https://doi.org/10.3390/rs12040595

Chicago/Turabian Style

Wu, Jinhui, and Shunlin Liang. 2020. "Assessing Terrestrial Ecosystem Resilience using Satellite Leaf Area Index" Remote Sensing 12, no. 4: 595. https://doi.org/10.3390/rs12040595

APA Style

Wu, J., & Liang, S. (2020). Assessing Terrestrial Ecosystem Resilience using Satellite Leaf Area Index. Remote Sensing, 12(4), 595. https://doi.org/10.3390/rs12040595

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop