Bistatic High-Frequency Radar Cross-Section of the Ocean Surface with Arbitrary Wave Heights
Abstract
:1. Introduction
2. First-Order Bistatic Electric Field Scattered from an Ocean Surface with Arbitrary Heights
3. First-Order Radar Cross-Section of the Ocean Surface with Arbitrary Heights
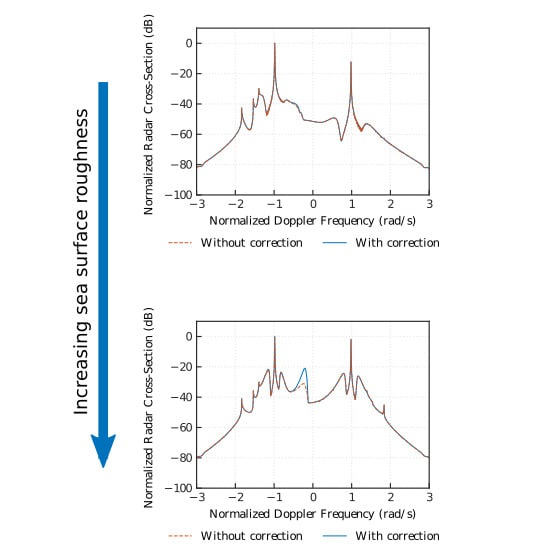
4. Simulation Results
5. Discussion
6. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
References
- Crombie, D.D. Doppler spectrum of sea echo at 13.56 Mc./s. Nature 1955, 175, 681–682. [Google Scholar] [CrossRef]
- Barrick, D.E. HF radio oceanography—A review. Bound-Lay. Meteorol. 1978, 13, 23–43. [Google Scholar] [CrossRef]
- Hardman, R.L.; Wyatt, L.R. Inversion of HF radar Doppler spectra using a neural network. J. Mar. Sci. Eng. 2019, 7, 255. [Google Scholar] [CrossRef] [Green Version]
- Sun, W.; Huang, W.; Ji, Y.; Dai, Y.; Ren, P.; Zhou, P.; Hao, X. A vessel azimuth and course joint re-estimation method for compact HFSWR. IEEE Trans. Geosci. Remote Sens. 2019, 1–11. [Google Scholar] [CrossRef]
- Sun, W.; Huang, W.; Ji, Y.; Dai, Y.; Ren, P.; Zhou, P. Vessel tracking with small-aperture compact high-frequency surface wave radar. In Proceedings of the OCEANS 2019—Marseille, Marseille, France, 17–20 June 2019; pp. 1–4. [Google Scholar] [CrossRef]
- Pidgeon, V.W. Bistatic cross section of the sea. IEEE Trans. Antennas Propag. 1966, 14, 405–406. [Google Scholar] [CrossRef]
- Peterson, A.M.; Teague, C.C.; Tyler, G.L. Bistatic-radar observation of long-period, directional ocean-wave spectra with Loran A. Science 1970, 170, 158–161. [Google Scholar] [CrossRef]
- Teague, C.C. Bistatic-radar techniques for observing long-wavelength directional ocean-wave spectra. IEEE Trans. Geosci. Electron. 1971, 9, 211–215. [Google Scholar] [CrossRef]
- Teague, C.C.; Vesecky, J.F.; Fernandez, D.M. HF radar instruments, past to present. Oceanography 1997, 10, 40–44. [Google Scholar] [CrossRef]
- Barrick, D.E. The interaction of HF/VHF radio waves with the sea surface and its implications. In AGARD Conference Proceedings No. 77 on Electromagnetics of the Sea; Aerospace Research & Development (AGARD), Ed.; National Atlantic Threaty Organization (NATO): Washington, DC, USA, 1970; number AGARD-CP-77-70; pp. 18-1–18-25. [Google Scholar]
- Barrick, D.E. Remote sensing of sea state by radar. In Remote Sensing of the Troposphere; Derr, V., Ed.; U.S. Department of Commerce—National Oceanic and Atmospheric Administration: Boulder, CO, USA, 1972; Chapter 12; pp. 12-1–12-46. [Google Scholar]
- Johnstone, D.L. Second-Order Electromagnetic and Hydromagnetic Effects in High-Frequency Radio-Wave Scattering from the Sea. Ph.D. Thesis, Stamford, CA, USA, 1975. [Google Scholar]
- Anderson, S.J.; Anderson, W.C. Bistatic HF scattering from the ocean surface and its application to remote sensing of seastate. In Proceedings of the 1987 IEEE APS International Symposium, Blacksburg, VA, USA, 15–19 June 1987. [Google Scholar]
- Anderson, S.J.; Fuks, I.M.; Praschifka, J. Multiple scattering of HF radio waves propagating across the sea surface. Wave. Random Media 1998, 8, 283–302. [Google Scholar] [CrossRef]
- Anderson, S.J. Directional wave spectrum measurement with multistatic HF surface wave radar. In Taking the Pulse of the Planet: The Role of Remote Sensing in Managing the Environment. Proceedings (Cat. No.00CH37120); IEEE: Honolulu, HI, USA, 2000. [Google Scholar] [CrossRef]
- Walsh, J.; Gill, E.W. An analysis of the scattering of high-frequency electromagnetic radiation from rough surfaces with application to pulse radar operating in backscatter mode. Radio Sci. 2000, 35, 1337–1359. [Google Scholar] [CrossRef] [Green Version]
- Gill, E.W.; Walsh, J. Bistatic form of the electric field equations for the scattering of vertically polarized high-frequency ground wave radiation from slightly rough, good conducting surfaces. Radio Sci. 2000, 35, 1323–1335. [Google Scholar] [CrossRef]
- Gill, E.W.; Walsh, J. High-frequency bistatic cross sections of the ocean surface. Radio Sci. 2001, 36, 1459–1475. [Google Scholar] [CrossRef]
- Gill, E.W.; Huang, W.; Walsh, J. On the development of a second-order bistatic radar cross section of the ocean surface: A high-frequency result for a finite scattering patch. IEEE J. Ocean. Eng. 2006, 31, 740–750. [Google Scholar] [CrossRef]
- Chen, S.; Huang, W.; Gill, E.W. First-order bistatic high-frequency radar power for mixed-path ionosphere-ocean propagation. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1940–1944. [Google Scholar] [CrossRef]
- Ma, Y.; Gill, E.W.; Huang, W. First-order bistatic high-frequency radar ocean surface cross-section for an antenna on a floating platform. IET Radar Sonar Navig. 2016, 10, 1136–1144. [Google Scholar] [CrossRef] [Green Version]
- Ma, Y.; Huang, W.; Gill, E.W. The second-order bistatic high-frequency radar cross section of ocean surface for an antenna on a floating platform. Can. J. Remote Sens. 2016, 42, 332–343. [Google Scholar] [CrossRef]
- Ma, Y.; Gill, E.W.; Huang, W. Bistatic high-frequency radar ocean surface cross section incorporating a dual-frequency platform motion model. IEEE J. Ocean. Eng. 2018, 43, 205–210. [Google Scholar] [CrossRef]
- Grosdidier, S.; Forget, P.; Barbin, Y.; Gúerin, C.A. HF bistatic ocean Doppler spectra: simulation versus experimentation. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2138–2148. [Google Scholar] [CrossRef] [Green Version]
- Barrick, D.E. Theory of HF and VHF propagation across the rough sea, 1, the effective surface impedance for a slightly rough highly conducting medium at grazing incidence. Radio Sci. 1971, 6, 517–526. [Google Scholar] [CrossRef]
- Wyatt, L.R. High order nonlinearities in HF radar backscatter from the ocean surface. IEE Proc. Radar Sonar Navig. 1995, 142, 293. [Google Scholar] [CrossRef]
- Massel, S.R. Ocean Surface Waves: Their Physics and Prediction, 3rd ed.; World Scientific Publishing: Singapore, 2017; p. 776. [Google Scholar]
- Silva, M.T.; Gill, E.W.; Huang, W. First-order high-frequency scattering for ocean surfaces with large roughness scales. Presented at the 28th Annual Newfoundland Electrical and Computer Engineering Conference (NECEC 2019), St. John’s, NL, Canada, 19 November 2019. [Google Scholar]
- Walsh, J. Asymptotic expansion of a Sommerfeld integral. Electron. Lett. 1984, 20, 746. [Google Scholar] [CrossRef]
- Weber, B.L.; Barrick, D.E. On the nonlinear theory for gravity waves on the ocean’s surface. Part I: derivations. J. Phys. Oceanogr. 1977, 7, 3–10. [Google Scholar] [CrossRef]
- Hasselmann, K. On the non-linear energy transfer in a gravity-wave spectrum Part 1. General theory. J. Fluid Mech. 1962, 12, 481. [Google Scholar] [CrossRef]
- Gill, E.W. The Scattering of High Frequency Electromagnetic Radiation from the Ocean Surface: An Analysis Based on a Bistatic Ground Wave Radar Configuration. Ph.D. Thesis, Memorial University of Newfoundland, St. John’s, NL, Canada, 1999. [Google Scholar]
- Cox, C.; Munk, W. Measurement of the roughness of the sea surface from photographs of the sun’s glitter. J. Opt. Soc. Am. 1954, 44, 838. [Google Scholar] [CrossRef]
- Gleason, S.; Zavorotny, V.U.; Akos, D.M.; Hrbek, S.; PopStefanija, I.; Walsh, E.J.; Masters, D.; Grant, M.S. Study of surface wind and mean square slope correlation in hurricane Ike with multiple sensors. IEEE J. Sel. Topics Appl. Earth Observ. Remote Sens. 2018, 11, 1975–1988. [Google Scholar] [CrossRef]
- Wu, J. Mean square slopes of the wind-disturbed water surface, their magnitude, directionality, and composition. Radio Sci. 1990, 25, 37–48. [Google Scholar] [CrossRef]
- Hwang, P.A. Wave number spectrum and mean square slope of intermediate-scale ocean surface waves. J. Geophys. Res. 2005, 110. [Google Scholar] [CrossRef] [Green Version]
- Katzberg, S.J.; Torres, O.; Ganoe, G. Calibration of reflected GPS for tropical storm wind speed retrievals. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef] [Green Version]
- Pierson, W.J.; Moskowitz, L. A Proposed Spectral form for Fully Developed Wind Seas Based on the Similarity Theory of S. A. Kitaigorodskii; Technical Report; U.S. Naval Oceanographic Office: New York, NY, USA, 1963. [Google Scholar]
- Longuet-Higgins, M.S. The effect of non-linearities on statistical distributions in the theory of sea waves. J. Fluid Mech. 1963, 17, 459. [Google Scholar] [CrossRef]
- Mitsuyasu, H.; Tasai, F.; Suhara, T.; Mizuno, S.; Ohkusu, M.; Honda, T.; Rikiishi, K. Observations of the directional spectrum of ocean waves using a cloverleaf buoy. J. Phys. Oceanogr. 1975, 5, 750–760. [Google Scholar] [CrossRef] [Green Version]



| MSS Slope Model | Total Root-Mean-Square Slope | |
|---|---|---|
| m/s | m/s | |
| Cox and Munk (1954) [33] | 0.22206 | 0.31477 |
| Wu (1990) [35] | 0.22319 | 0.30573 |
| Hwang (2005) [36] | 0.22252 | 0.32197 |
| Katzberg, Torres and Ganoe (2006) [37] | 0.15098 | 0.18104 |
| Gleason et al. (2018) [34] | 0.16119 | 0.18041 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Silva, M.T.; Huang, W.; Gill, E.W. Bistatic High-Frequency Radar Cross-Section of the Ocean Surface with Arbitrary Wave Heights. Remote Sens. 2020, 12, 667. https://doi.org/10.3390/rs12040667
Silva MT, Huang W, Gill EW. Bistatic High-Frequency Radar Cross-Section of the Ocean Surface with Arbitrary Wave Heights. Remote Sensing. 2020; 12(4):667. https://doi.org/10.3390/rs12040667
Chicago/Turabian StyleSilva, Murilo Teixeira, Weimin Huang, and Eric W. Gill. 2020. "Bistatic High-Frequency Radar Cross-Section of the Ocean Surface with Arbitrary Wave Heights" Remote Sensing 12, no. 4: 667. https://doi.org/10.3390/rs12040667
APA StyleSilva, M. T., Huang, W., & Gill, E. W. (2020). Bistatic High-Frequency Radar Cross-Section of the Ocean Surface with Arbitrary Wave Heights. Remote Sensing, 12(4), 667. https://doi.org/10.3390/rs12040667