A Novel GNSS Attitude Determination Method Based on Primary Baseline Switching for A Multi-Antenna Platform
Abstract
:1. Introduction
2. Methodology
2.1. DD Positioning Algorithm Based on Carrier Phase
2.2. Attitude Determination Method
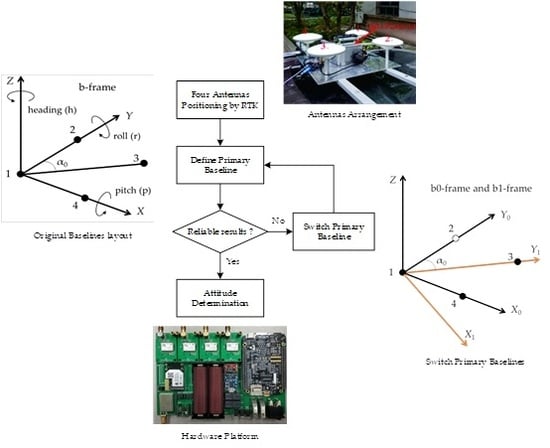
2.3. Primary Baseline Switching
2.4. Error Analysis
3. Introduction to the Platform
4. Experiment Results and Analysis
4.1. Acquisition of Reference Results
4.2. The Correctness of the Primary Baseline Switching Method
4.3. Analysis of the Results Based on Primary Baseline Switching Method
4.3.1. Valid Epoch Proportion
4.3.2. Results of Attitude Determination Based on the Proposed Method
4.3.3. Error Analysis
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Li, Y.; Efatmaneshnik, M.; Dempster, A. Attitude Determination by Integration of MEMS Inertial Sensors and GPS for Autonomous Agriculture Applications. GPS Solut. 2012, 16, 41–52. [Google Scholar] [CrossRef]
- Liu, S.; Sun, F.; Zhang, L.; Li, W.; Zhu, X. Tight integration of ambiguity-fixed ppp and ins: Model description and initial results. GPS Solut. 2016, 20, 39–49. [Google Scholar] [CrossRef]
- Rabbou, M.A.; El-Rabbany, A. Tightly Coupled Integration of GPS Precise Point Positioning and MEMS-based Inertial Systems. GPS Solut. 2015, 19, 601–609. [Google Scholar] [CrossRef]
- Lau, L.; Cross, P.; Steen, M. Flight Tests of Error-Bounded Heading and Pitch Determination with Two GPS Receivers. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 388–404. [Google Scholar] [CrossRef]
- Yinzhi, Z.; Peng, Z.; Jiming, G.; Xin, L.; Jinling, W.; Fei, Y.; Xinzhe, W. A new method of high-precision positioning for an indoor pseudolite without using the known point initialization. Sensors. 2018, 18, 1977. [Google Scholar]
- Xiaobo, C.; Houze, X.U.; Yong, W.; Hua, C.; Leixiang, D. Direct attitude determination method based on vehicle-mounted three-antenna gnss and the accuracy evaluation. Geomat. Inf. Sci. Wuhan Univ. 2018, 43, 820–825. [Google Scholar]
- Wahba, G. A Least Squares Estimate of Satellite Attitude. Siam Rev. 1965, 7, 384–386. [Google Scholar] [CrossRef]
- Shuster, M.D. Approximate Algorithms for Fast Optimal attitude Computation. In Proceedings of the AIAA Guidance and Control conference, Palo Alto, CA, USA, 7–9 August 1978; pp. 88–95. [Google Scholar]
- Markley, F.L. Attitude Determination Using Vector Observations and the Singular Value Decomposition. J. Astronaut. Sci. 1988, 36, 245–258. [Google Scholar]
- Chen, W.; Hu, K.; Li, E. Low-cost land vehicle attitude determination using single-epoch GPS data, MEMS-based inclinometer measurements. Acta Geod. Geophys. 2016, 52, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Lee, B.; Lee, Y.J.; Sung, S. Attitude Determination Algorithm based on Relative Quaternion Geometry of Velocity Incremental Vectors for Cost Efficient AHRS Design. Int. J. Aeronaut. Space Sci. 2018, 7, 1–11. [Google Scholar] [CrossRef]
- Teunissen, P.J.G. Integer least-squares theory for the GNSS compass. J. Geod. 2010, 84, 443–447. [Google Scholar] [CrossRef] [Green Version]
- Giorgi, G.; Teunissen, P.J.G.; Verhagen, S.; Buist, P.J. Improving the GNSS Attitude Ambiguity Success Rate with the Multivariate Constrained LAMBDA Method. In Geodesy for Planet Earth; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Yingdong, Y.; Xuchu, M.; Weifeng, T. Rotation Matrix Method Based on Ambiguity Function for GNSS Attitude Determination. Sensors. 2016, 16, 841. [Google Scholar]
- Cong, L.; Li, E.; Qin, H.; Ling, K.; Xue, R. A performance improvement method for low-cost land vehicle gps/mems-ins attitude determination. Sensors. 2015, 15, 5722–5746. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tian, Z.; Zhang, Y.; Zhou, M.; Wu, Z. Carrier Phase Based Attitude Determination Using Tightly Coupled BDS/INS. In Proceedings of the International Conference in Communications, Signal Processing, and Systems, Dalian, China, 14–16 July 2018; Springer: Singapore.
- Xu, T.; Xu, L.; Tian, X.; Li, X. GPS-aided method for platform attitude determination based on target images. Appl. Opt. 2017, 56, 2378. [Google Scholar] [CrossRef] [PubMed]
- Na, L.; Lin, Z.; Liang, L.; Chun, J. Integrity monitoring of high-accuracy gnss-based attitude determination. GPS Solut. 2018, 22, 120. [Google Scholar]
- Guo, J. Quality assessment of the affine-constrained GNSS attitude model. GPS Solut. 2019, 23, 24. [Google Scholar] [CrossRef]
- De Celis, R.; Cadarso, L. An Estimator for UAV Attitude Determination based on Accelerometers, GNSS Sensors, and Aerodynamic Coefficients. Navigation. 2018, 65, 319–334. [Google Scholar] [CrossRef]
- Zhang, X.; Yang, Z.; Zhang, T.; Shen, Y. An improved Kalman filter for attitude determination of multi-rotor UAVs based on low-cost MEMS sensors. In Proceedings of the Guidance, Navigation & Control Conference, Salzburg, Austria, 29 May–2 June 2017. [Google Scholar]
- André, H.; Mohr, U.; Markgraf, M.; Montenbruck, O. Flight results of gps-based attitude determination for the microsatellite flying laptop. Navigation. 2019, 66, 277–287. [Google Scholar]
- Ballal, T.; Bleakley, C.J. Gnss instantaneous ambiguity resolution and attitude determination exploiting the receiver antenna configuration. IEEE Trans. Aerosp. Electron. Syst. 2014, 50, 2061–2069. [Google Scholar] [CrossRef] [Green Version]
- Chen, W.; Qin, H. New method for single epoch, single frequency land vehicle attitude determination using low-end GPS receiver. GPS Solut. 2012, 16, 329–338. [Google Scholar] [CrossRef]
- Teunissen, P.J.G. The affine constrained GNSS attitude model and its multivariate integer least-squares solution. J. Geod. 2012, 86, 547–563. [Google Scholar] [CrossRef] [Green Version]
- Wu, Z.; Yao, M.; Ma, H.; Jia, W.; Tian, F. Low-Cost Antenna Attitude Estimation by Fusing Inertial Sensing and Two-Antenna GPS for Vehicle-Mounted Satcom-on-the-Move. IEEE Trans. Veh. Technol. 2013, 62, 1084–1096. [Google Scholar] [CrossRef]
- Wu, Z.; Yao, M.; Ma, H.; Jia, W. Low-cost attitude estimation with mimu and two-antenna gps for satcom-on-the-move. GPS Solut. 2013, 17, 75–87. [Google Scholar] [CrossRef]
- Xu, G. GPS: Theory, Algorithms and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Kouba, J. A Guide to Using International GNSS Service (IGS) Products. Available online: http://acc.igs.org/UsingIGSProductsVer21.pdf. 2009 (accessed on 15 December 2019).
- Shi, J.; Yuan, X.; Cai, Y.; Wang, G. GPS Real-time Precise Point Positioning for Aerial Triangulation. GPS Solut. 2017, 21, 405–414. [Google Scholar] [CrossRef]
- Shi, J.; Gao, Y. A comparison of three PPP integer ambiguity resolution methods. GPS Solut. 2014, 18, 519–528. [Google Scholar] [CrossRef]
- Liu, Y.; Lian, B. Indoor pseudolite relative localization algorithm with kalmanfilter. Acta Phys. Sin. 2014, 63, 1–7. [Google Scholar]
- Cellmer, S.; Wielgosz, P.; Rzepecka, Z. Modified ambiguity function approach for GPS carrier phase positioning. J. Geod. 2010, 84, 267–275. [Google Scholar] [CrossRef]
- Alfred, L. GPS Satellite Surveying, 3rd ed.; Wiley: New York, NY, USA, 2004. [Google Scholar]
- Teunissen, P.J.G.; Kleusberg, A. GPS for Geodesy; Springer: Berlin/Heidelberg, Germany, 1998. [Google Scholar]
- Teunissen, P.J.G. Least-Squares Estimation of the Integer GPS ambiguities. In Proceedings of the Invited Lecture, Section IV Theory and Methodology, IAG General Meeting, Beijing, China, 8–13 August 1993. 14–16 July 2018. [Google Scholar]
- Teunissen, P.J.G. The least-squares ambiguity decorrelation adjustment: A method for fast GPS integer ambiguity estimation. J. Geod. 1995, 70, 65–82. [Google Scholar] [CrossRef]
- Groves, P.D. Principles of GNSS, Inertial, and Multisensor Integrated Navigation Systems, 2nd ed.; Artech House: Boston, MA, USA, 2013. [Google Scholar]













| Attitude | alpha | Maximum/deg | Minimum/deg | Mean/deg | RMS/deg | Variance/deg2 |
|---|---|---|---|---|---|---|
| Δh | −45° | 2.64 | −0.89 | 0.06 | 0.34 | 0.11 |
| −90° | 2.97 | −2.11 | 0.74 | 1.04 | 0.53 | |
| Δp | −45° | 3.87 | −4.64 | −1.06 | 2.04 | 3.06 |
| −90° | 3.99 | −4.65 | −1.06 | 2.03 | 2.99 | |
| Δr | −45° | 4.58 | −5.37 | −0.22 | 1.62 | 2.58 |
| −90° | 2.53 | −3.17 | 0.50 | 0.95 | 0.65 |
| Mode | Total Epochs | Valid Epochs | Proportion |
|---|---|---|---|
| No switching | 919 | 662 | 72.03% |
| Allowing switching | 919 | 769 | 83.68% |
| Periods | Start | End | Total Epochs | Valid Epochs | Switching Epochs |
|---|---|---|---|---|---|
| 1 | 1 s | 265 s | 265 | 88 | 84 |
| 2 | 409 s | 423 s | 15 | 0 | 15 |
| 3 | 697 s | 704 s | 8 | 0 | 8 |
| Period | No Switching | Allowing Switching | ||||
|---|---|---|---|---|---|---|
| Heading | Pitch | Roll | Heading | Pitch | Roll | |
| 1 | 38.14 | 13.02 | 25.25 | 0.74 | 1.72 | 1.53 |
| 2 | 0.29 | 0.99 | 0.73 | 0.24 | 0.68 | 0.66 |
| 3 | 0.28 | 1.01 | 0.53 | 0.11 | 0.49 | 0.28 |
| Attitude | Maximum/deg | Minimum/deg | Mean/deg | RMS/deg | Variance/deg2 |
|---|---|---|---|---|---|
| Δh | 1.79 | −2.36 | −0.32 | 0.53 | 0.28 |
| Δp | 3.66 | −3.71 | 0.76 | 1.25 | 1.56 |
| Δr | 3.52 | −3.50 | −0.43 | 1.16 | 1.34 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, P.; Zhao, Y.; Lin, H.; Zou, J.; Wang, X.; Yang, F. A Novel GNSS Attitude Determination Method Based on Primary Baseline Switching for A Multi-Antenna Platform. Remote Sens. 2020, 12, 747. https://doi.org/10.3390/rs12050747
Zhang P, Zhao Y, Lin H, Zou J, Wang X, Yang F. A Novel GNSS Attitude Determination Method Based on Primary Baseline Switching for A Multi-Antenna Platform. Remote Sensing. 2020; 12(5):747. https://doi.org/10.3390/rs12050747
Chicago/Turabian StyleZhang, Peng, Yinzhi Zhao, Huan Lin, Jingui Zou, Xinzhe Wang, and Fei Yang. 2020. "A Novel GNSS Attitude Determination Method Based on Primary Baseline Switching for A Multi-Antenna Platform" Remote Sensing 12, no. 5: 747. https://doi.org/10.3390/rs12050747
APA StyleZhang, P., Zhao, Y., Lin, H., Zou, J., Wang, X., & Yang, F. (2020). A Novel GNSS Attitude Determination Method Based on Primary Baseline Switching for A Multi-Antenna Platform. Remote Sensing, 12(5), 747. https://doi.org/10.3390/rs12050747