2.1. Deep Semantic Segmentation Neural Networks’ Classification Strategy and Post-Processing
Deep semantic segmentation neural networks such as FCNs, SegNET, and U-NET have been widely studied and applied by the remote sensing image classification research community. The training and classification processes of these networks are illustrated in
Figure 1.
As shown in
Figure 1, the end-to-end classification strategy is usually adopted for DSSNNs’ training and classification. During the training stage, a set of remote sensing images
ImageSet = {
I1,
I2, …,
In} is adopted and manually interpreted into a ground truth set
GroundTruthSet = {
Igt1,
Igt2, …,
Igtn}; then, the
GroundTruthSet is separated into patches to construct the training dataset. The classification model
Mendtoend is obtained based on this training dataset. During the classification stage, the classification model is utilized to classify a completely new remote sensing image
Inew (not an image from
ImageSet). This strategy achieves a higher degree of automation; the classification process has no relationship with the training data or the training algorithm, and newly obtained or other images in the same area can be classified automatically with
Mendtoend, forming an input-to-output/end-to-end structure. Thus, this strategy is more valuable in practical applications when massive amounts of remote sensing data need to be processed quickly.
However, the classification results of the end-to-end classification strategy are usually not "perfect", and they are affected by two factors. On the one hand, because the training data are constructed by manual interpretation, it is difficult to provide training ground truth images that are precise at the pixel level (especially at the boundaries of ground objects). Moreover, the incorrectly interpreted areas of these images may even be amplified through the repetitive training process [
16]. On the other hand, during data transfer among the neural network layers, along with obtaining high-level spatial features, some spatial context information may be lost [
35]. Therefore, the classification results obtained by the "end-to-end classification strategy" may result in many flaws, especially at ground object boundaries. To correct these flaws, in the computer vision research field, the conditional random field (CRF) method is usually adopted in the post-processing stage to correct the result image. The conditional random field can be defined as follows:
where
F is a set of random variables {
F1,
F2, …,
FN};
Fi is a pixel vector;
X is a set of random variables {
x1,
x2, …,
xN}, where
xi is the category label of pixel
i;
Z(
F) is a normalizing factor; and
c is a clique in a set of cliques
Cg, where
g induces a potential
φc [
23,
24]. By calculating Equation (1), the CRF adjusts the category label of each pixel and achieves the goal of correcting the result image. The CRF is highly effective at processing images that contain only a small number of objects. However, the numbers, sizes, and locations of objects in remote sensing images vary widely, and the traditional CRF tends to perform a global optimization of the entire image. This process leads to some ground objects being excessively enlarged or reduced. Furthermore, if the different parts of ground objects that are shadowed or not shadowed are processed in the same manner, the CRF result will contain more errors [
31]. In our previous work, we proposed a method called the restricted conditional random field (RCRF) that can handle the above situation [
31]. Unfortunately, the RCRF requires the introduction of samples to control its iteration termination and produce an output integrated image. When integrated into the classification process, the need for samples will cause the whole classification process to lose its end-to-end characteristic; thus, the RCRF cannot be integrated into an end-to-end process. In summary, to address the above problems, the traditional CRF method needs to be further improved by adding the following characteristics:
(1) End-to end result image evaluation: Without requiring samples, the method should be able to automatically identify which areas of a classification result image may contain errors. By identifying areas that are strongly suspected of being misclassified, we can limit the CRF process and analysis scope.
(2) Localized post-processing: The method should be able to transform the entire image post-processing operation into local corrections and separate the various objects or different parts of objects (such as roads in shadow or not in shadow) into sub-images to alleviate the negative impacts of differences in the number, size, location, and brightness of objects.
To achieve this goal, a new mechanism must be introduced to improve the traditional CRF algorithm for remote sensing classification results post-processing.
2.2. End-to-End Result Image Evaluation and Localized Post-Processing
The majority of evaluation methods for classification results require samples with category labels that allow the algorithm to determine whether the classification result is good; however, to achieve an end-to-end classification results evaluation, samples cannot be required during the evaluation process. In the absence of testing samples, although it is impossible to accurately indicate which pixels are incorrectly classified, we can still find some areas that are highly suspected of having classification errors by applying some conditions.
Therefore, we need to establish a relation between the remote sensing image and the classification result image and find the areas where the colors (bands) of the remote sensing image are consistent, but the classification results are inconsistent; these are the areas that may belong to the same object but are incorrectly classified into different categories. Such areas are strong candidates for containing incorrectly classified pixels. Furthermore, we try to correct these errors within a relatively small area.
To achieve the above goals, for a remote sensing image
Iimage and its corresponding classification image
Icls, the methods proposed in this paper are illustrated in
Figure 2:
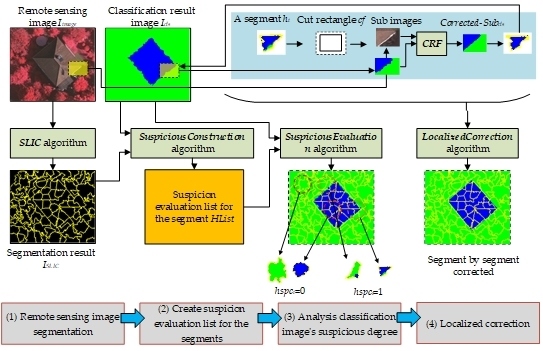
As shown in
Figure 2, we use four steps to perform localized correction:
(1) Remote sensing image segmentation
We need to segment the remote image based on color (band value) consistency. In this paper, we adopt the simple linear iterative clustering (SLIC) algorithm as the segmentation method. The algorithm initially contains
k clusters. Each cluster is denoted by
Ci = {
li,
ai,
bi,
xi,
yi}, where
li,
ai, and
bi are the color values of
Ci in CIELAB color space, and
xi,
yi are the center coordinates of
Ci in the image. For two clusters,
Ci and
Cj, the SLIC algorithm is introduced to compare color and space distances simultaneously, as follows:
where
distancecolor is the color distance and
distancespace is the spatial distance. Based on these two distances, the distance between the two clusters is:
where
Ncolor is the maximum color distance and
Nspace is the maximum position distance. The SLIC algorithm uses the iterative mechanism of the
k-means algorithm to gradually adjust the cluster position and the cluster to which each pixel belongs, eventually obtaining
Nsegment segments [
36]. The advantage of the SLIC algorithm is that it can quickly and easily cluster adjacent similar regions into a segment; this characteristic is particularly useful for finding adjacent areas that have a consistent color (band value). For
Iimage, the SLIC algorithm is used to obtain the segmentation result
ISLIC. In each segment in
ISLIC, the pixels are assigned the same segment label.
(2) Create a list of segments with suspicious degree evaluations
For all the segments in
ISLIC, a suspicion evaluation list for the segments
HList = {
h1,
h2, …,
hn} is constructed, where
hi is a set
hi = {
hidi,
hpixelsi,
hreci,
hspci},
hidi is a segment label,
hpixelsi holds the locations of all the pixels in the segment;
hreci is the location and size of the enclosing frame rectangle of
hpixelsi; and
hspci is a suspicious evaluation value, which is either 0 or 1—a “1” means that the pixels in the segment are suspected of being misclassified, and a “0” means that the pixels in the segment are likely correctly classified. The algorithm to construct the suspicious degree evaluation list is as follows (SuspiciousConstruction Algorithm):
| Algorithm SuspiciousConstruction |
| Input:ISLIC |
| Output:HList |
| Begin |
| HList = an empty list; |
| foreach (segment label i in ISLIC){ |
| hidi = i; |
| hpixelsi = Locations of all the pixels in corresponding segment i; |
| hreci= the location and size of hpixelsi’s enclosing frame rectangle; |
| hspci = 0; |
| hi = Create a set {hidi, hpixelsi, hreci, hhypi}; |
| HList ← hi; |
| } |
| return HList; |
| End |
In the SuspiciousConstruction algorithm, by default, each segment’s spci = 0 (the hypothesis is that no misclassified pixels exist in the segment).
(3) Analyze the suspicious degree
As shown in
Figure 2, for a segment, the
spci value can be calculated based on the pixels in
ISLIC;
hi’s corresponding pixels can be grouped as
SP = {
sp1,
sp2, …,
spm}, where
spi is the pixel number belonging to category
i, and the inconsistency degree of
SP can be described using the following formula:
Based on this formula, the value of
hypi can be expressed as follows:
where
α is a threshold value (the default is 0.05). When a segment’s
hspci = 0, the segment’s corresponding pixels in
ISLIC all belong to the same category, which indicates that pixels’ features are consistent in both
Iimage (band value) and
ISLIC (segment label); in this case, the segment does not need correction by CRF. In contrast, when a segment’s
hspci = 1, the pixels of the segment in
ISLIC belong to different categories, but the pixel’s color (band value) is comparatively consistent in
Iimage; this case may be further subdivided into two situations:
A. Some type of classification error exists in the segment (such as the classification result deformation problem appearing on an object boundary).
B. The classification result is correct, but the segment crosses a boundary between objects in ISLIC (for example, the number of segments assigned to the SLIC algorithm is too small, and some areas are undersegmented).
In either case, we need to be suspicious of the corresponding segment and attempt to correct mistakes using CRF. Based on Formulas 5 and 6, the algorithm for analyzing
Icls using
HList is as follows (SuspiciousEvaluation Algorithm):
| Algorithm SuspiciousEvaluation |
| Input:HList, Icls |
| Output:HList |
| Begin |
| foreach(Item hi in HList){ |
| SP = new m-element array with zero values |
| foreach(Location pl in hi.hpixelsi){ |
| px = Obtain pixel at pl in Icls; |
| pxcl = Obtain category label of px; |
| SP[pxcl] = SP[pxcl] + 1; |
| } |
| inconsistence = Use Formula (5) to calculate SP; |
| hi.hypi = Use Formula (6) with inconsistence |
| } |
| return HList; |
| End |
By applying the SuspiciousEvaluation algorithm, we can identify which segments are suspicious and require further post-processing.
(4) Localized correction
As shown in
Figure 2, for a segment
hi that is suspected of containing error classified pixels, the post-processing strategy can be described as follows: First, based on
hi.hreci, create a cut rectangle
cf, (
cf = rectangle
hi.hreci enlarged by
β pixels), where
β is the number of pixels to enlarge and the default value is 10. Second, use the
cf cut sub-images from
Iimage and
Icls to obtain a
Subimage and a
Subcls. Third, input
Subimage and
Subcls to the CRF algorithm, and obtain a corrected classification result
Corrected-
Subcls. Finally, based on the pixel locations in
hi.hpixelsi, obtain the pixels from
Corrected-
Subcls and write them to
Icls, which constitutes localized area correction on
Icls. For the entire
Icls, the localized correction algorithm on
Icls is as follows (LocalizedCorrection Algorithm):
| Algorithm LocalizedCorrection |
| Input:Icls, HList |
| Output:Icls |
| Begin |
| foreach(hi in HList){ |
| if (hi.hspci==0) then continue; |
| cf= Enlarge rectangle hi.hreci by β pixels; |
| Subimage, Subcls = Cut sub-images from Iimage and Icls; |
| Corrected-Subcls = Process Subimage and Subcls by CRF algorithm; |
| pixels = Obtain pixels in hi.hpixelsi from Corrected-Subcls; |
| Icls←pixels; |
| } |
| return Icls |
| End |
By applying the LocalizedCorrection algorithm, the ICLS will be corrected segment by segment through the CRF algorithm.
2.3. Overall Process of the End-to-End and Localized Post-Processing Method
Based on the four steps and algorithms described in the preceding subsection, we can evaluate the classification result image without requiring testing samples and correct the classification result image within local areas. By integrating these algorithms, we propose an end-to-end and localized post-processing method (ELP) whose input is a remote sensing image
Iimage and a classification result image
Icls, and whose output is the corrected classification result image. Through the iterative and progressive correction process, the goal of improving the quality of the
ICLS can be achieved. The process of ELP is shown in
Figure 3.
As
Figure 3 shows, the ELP method is a step-by-step iterative correction process that requires a total of γ iterations to correct the
Icls content. Before beginning the iteration, the ELP method obtains the segmentation result image
ISLIC before iteration:
Then, it evaluates the segments and constructs the suspicion evaluation list for the segments
HList:
In each iteration, ELP updates
HList to obtain
HListη, and it outputs a new classification result image
, where
η is the iteration value (in the range [1,γ]). The
i-th iteration’s output is:
When
η = 1,
HList0 =
HList, and
; when
η ≥ 2, the current iteration result depends on the result of the previous iteration. Based on the above two formulas, the ELP algorithm will update
HList and
Icls in each iteration;
HList indicates suspicious areas, and these areas are corrected and stored in
Icls. As the iteration progresses, the final result is obtained:
Through the above process, ELP achieves both the desired goals: end-to-end result image evaluation and localized post-processing.