Glacier Mass Balance in the Nyainqentanglha Mountains between 2000 and 2017 Retrieved from ZiYuan-3 Stereo Images and the SRTM DEM
Abstract
:1. Introduction
- (a)
- attitude swing or imaging simultaneously the same region from multiple satellites, which is deployed to respond to emergency conditions or special requirements, but cannot provide observations at regular time intervals over a long period of time;
- (b)
- revisiting the same region at short time intervals, but even though the revisit interval is short, the surface condition may change, as for example due to snowfall events.
- To develop an improved procedure to retrieve glacier mass balance from ZY-3 TLA stereo images;
- To evaluate the performance of ZY-3 stereo images in deriving glacier mass balance over the complex terrain in the ENM and relatively smoother terrain in the WNM;
- To cross-validate optical photogrammetry (ZY-3 TLA stereo images) and InSAR (TerraSAR-X and TanDEM-X image pairs) in capturing the spatial patterns of glacier mass balance and explore their differences;
- To compare and analyze the trends in the mass balance of glaciers responding to maritime climate in the ENM and to subcontinental climate in the WNM in the first decade (2000–2013) and in recent years (2013–2017).
2. Study Area and Datasets
2.1. Study Area
2.2. Datasets
2.2.1. ZY-3
2.2.2. SRTM
2.2.3. Glacier Elevation Change Map from DInSAR
2.2.4. Landsat TM data
3. Methodology
3.1. ZY-3 DEM Raster Data Generation
3.1.1. Stereo Image Processing of ZY-3 TLA Data
3.1.2. Co-Registration of Point Clouds
3.1.3. Fusion of Multiple Point Clouds
3.2. Glacier Mass Balance Estimation
4. Results
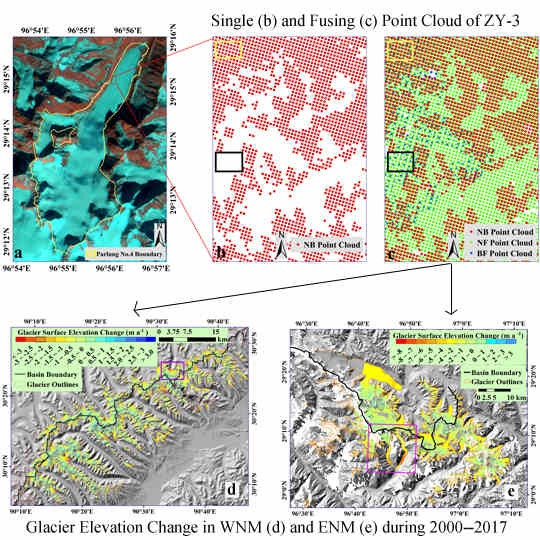
4.1. Comparison of ZY-3 TLA Data with Single Stereo View Data.
4.2. The Accuracy of ZY-3 TLA Data in Producing a DEM
4.3. Glacier Mass Balance in the WNM
4.4. Glacier Mass Balance in the ENM
4.5. Effects of Debris on Glacier Mass Balance
4.6. The Effect of Glacier Surface Slope on Glacier Elevation Change
5. Discussion
5.1. Internal Consistency of the Glacier Elevation Change Retrieved with the ZY-3 TLA Data
5.2. Cross-Comparison of ZY-3 TLA with Other Data Sources Results
5.3. Comparison with Previous Studies
5.4. Advantages and Disadvantages of ZY-3 TLA Data to Capture Glacier Mass Balance
6. Conclusions
Author Contributions
Funding
Acknowledgements
Conflicts of Interest
References
- Kaser, G.; Grosshauser, M.; Marzeion, B. Contribution potential of glaciers to water availability in different climate regimes. Proc. Natl. Acad. Sci. USA 2010, 107, 20223–20227. [Google Scholar] [CrossRef] [Green Version]
- Wang, W.C.; Xiang, Y.; Gao, Y.; Lu, A.X.; Yao, T.D. Rapid expansion of glacial lakes caused by climate and glacier retreat in the Central Himalayas. Hydrol. Process. 2015, 29, 859–874. [Google Scholar] [CrossRef]
- Zhou, Y.S.; Li, Z.W.; Li, J.; Zhao, R.; Ding, X.L. Glacier mass balance in the Qinghai Tibet Plateau and its surroundings from the mid-1970s to 2000 based on Hexagon KH-9 and SRTM DEMs. Remote Sens. Environ. 2018, 210, 96–112. [Google Scholar] [CrossRef]
- Kaab, A.; Berthier, E.; Nuth, C.; Gardelle, J.; Arnaud, Y. Contrasting patterns of early twenty-first-century glacier mass change in the Himalayas. Nature 2012, 488, 495–498. [Google Scholar] [CrossRef] [PubMed]
- Yao, T.D.; Thompson, L.; Yang, W.; Yu, W.S.; Gao, Y.; Guo, X.J.; Yang, X.X.; Duan, K.Q.; Zhao, H.B.; Xu, B.Q.; et al. Different glacier status with atmospheric circulations in Tibetan Plateau and surroundings. Nat. Clim. Chang. 2012, 2, 663–667. [Google Scholar] [CrossRef]
- Maurer, J.M.; Schaefer, J.M.; Rupper, S.; Corley, A. Acceleration of ice loss across the Himalayas over the past 40 years. Sci. Adv. 2019, 5. [Google Scholar] [CrossRef] [Green Version]
- Gardelle, J.; Berthier, E.; Arnaud, Y.; Kaab, A. Region-wide glacier mass balances over the Pamir-Karakoram-Himalaya during 1999–2011 (vol 7, pg 1263, 2013). Cryosphere 2013, 7, 1885–1886. [Google Scholar] [CrossRef] [Green Version]
- Immerzeel, W.W.; Kraaijenbrink, P.D.A.; Shea, J.M.; Shrestha, A.B.; Pellicciotti, F.; Bierkens, M.F.P.; de Jong, S.M. High-resolution monitoring of Himalayan glacier dynamics using unmanned aerial vehicles. Remote Sens. Environ. 2014, 150, 93–103. [Google Scholar] [CrossRef]
- Li, G.; Lin, H. Recent decadal glacier mass balances over the Western Nyaingentanglha Mountains and the increase in their melting contribution to Nam Co Lake measured by differential bistatic SAR interferometry. Glob. Planet. Chang. 2017, 149, 177–190. [Google Scholar] [CrossRef] [Green Version]
- Berthier, E.; Vincent, C.; Magnusson, E.; Gunnlaugsson, A.T.; Pitte, P.; Le Meur, E.; Masiokas, M.; Ruiz, L.; Palsson, F.; Belart, J.M.C.; et al. Glacier topography and elevation changes derived from Pleiades sub-meter stereo images. Cryosphere 2014, 8, 2275–2291. [Google Scholar] [CrossRef] [Green Version]
- Bolch, T.; Pieczonka, T.; Benn, D.I. Multi-decadal mass loss of glaciers in the Everest area (Nepal Himalaya) derived from stereo imagery. Cryosphere 2011, 5, 349–358. [Google Scholar] [CrossRef] [Green Version]
- Ragettli, S.; Bolch, T.; Pellicciotti, F. Heterogeneous glacier thinning patterns over the last 40 years in Langtang Himal, Nepal. Cryosphere 2016, 10, 2075–2097. [Google Scholar] [CrossRef] [Green Version]
- Brun, F.; Berthier, E.; Wagnon, P.; Kaab, A.; Treichler, D. A spatially resolved estimate of High Mountain Asia glacier mass balances from 2000 to 2016. Nat. Geosci. 2017, 10, 668–673. [Google Scholar] [CrossRef] [PubMed]
- Rieg, L.; Klug, C.; Nicholson, L.; Sailer, R. Pleiades Tri-Stereo Data for Glacier Investigations—Examples from the European Alps and the Khumbu Himal. Remote Sens. 2018, 10, 1563. [Google Scholar] [CrossRef] [Green Version]
- Tian, J.; Reinartz, P.; d’Angelo, P.; Ehlers, M. Region-based automatic building and forest change detection on Cartosat-1 stereo imagery. ISPRS J. Photogramm. Remote Sens. 2013, 79, 226–239. [Google Scholar] [CrossRef]
- Qin, R.J. Change detection on LOD 2 building models with very high resolution spaceborne stereo imagery. ISPRS J. Photogramm. Remote Sens. 2014, 96, 179–192. [Google Scholar] [CrossRef]
- Al-Rawabdeh, A.; He, F.N.; Moussa, A.; El-Sheimy, N.; Habib, A. Using an Unmanned Aerial Vehicle-Based Digital Imaging System to Derive a 3D Point Cloud for Landslide Scarp Recognition. Remote Sens. 2016, 8, 95. [Google Scholar] [CrossRef] [Green Version]
- Dall’Asta, E.; Forlani, G.; Roncella, R.; Santise, M.; Diotri, F.; di Cella, U.M. Unmanned Aerial Systems and DSM matching for rock glacier monitoring. ISPRS J. Photogramm. Remote Sens. 2017, 127, 102–114. [Google Scholar] [CrossRef]
- Meng, X.; Wang, L.; Silván-Cárdenas, J.L.; Currit, N. A multi-directional ground filtering algorithm for airborne LIDAR. ISPRS J. Photogramm. Remote Sens. 2009. [Google Scholar] [CrossRef] [Green Version]
- Mongus, D.; Žalik, B. Parameter-free ground filtering of LiDAR data for automatic DTM generation. ISPRS J. Photogramm. Remote Sens. 2012. [Google Scholar] [CrossRef]
- Skinner, B.; Vidal-Calleja, T.; Miro, J.V.; De Bruijn, F.; Falque, R. 3D point cloud upsampling for accurate reconstruction of dense 2.5 D thickness maps. In Proceedings of the Australasian Conference on Robotics and Automation, ACRA, Melbourne, Australia, 2–4 December 2014. [Google Scholar]
- Liu, S.; Yao, X.; Guo, W.; Junli, X.U.; Shangguan, D.; Wei, J.; Bao, W.; Lizong, W.U. The contemporary glaciers in China based on the Second Chinese Glacier Inventory. Acta Geogr. Sin. 2015, 70, 3–16. [Google Scholar]
- Zhou, S.; Kang, S.; Chen, F.; Joswiak, D.R. Water balance observations reveal significant subsurface water seepage from Lake Nam Co, south-central Tibetan Plateau. J. Hydrol. 2013, 491, 89–99. [Google Scholar] [CrossRef]
- Lei, Y.; Yao, T.; Bird, B.W.; Yang, K.; Zhai, J.; Sheng, Y. Coherent lake growth on the central Tibetan Plateau since the 1970s: Characterization and attribution. J. Hydrol. 2013, 483, 61–67. [Google Scholar] [CrossRef]
- Wu, B.Y. Weakening of Indian summer monsoon in recent decades. Adv. Atmos. Sci. 2005, 22, 21–29. [Google Scholar]
- Lin, H.; Li, G.; Cuo, L.; Hooper, A.; Ye, Q.H. A decreasing glacier mass balance gradient from the edge of the Upper Tarim Basin to the Karakoram during 2000–2014. Sci. Rep. 2017, 7. [Google Scholar] [CrossRef]
- Gautam, R.; Hsu, N.C.; Lau, W.K.M.; Yasunari, T.J. Satellite observations of desert dust-induced Himalayan snow darkening. Geophys. Res. Lett. 2013, 40, 988–993. [Google Scholar] [CrossRef] [Green Version]
- Ming, J.; Wang, Y.; Du, Z.; Zhang, T.; Guo, W.; Xiao, C.; Xu, X.; Ding, M.; Zhang, D.; Yang, W. Widespread albedo decreasing and induced melting of Himalayan snow and ice in the early 21st century. PLoS ONE 2015, 10. [Google Scholar] [CrossRef] [Green Version]
- Kodamana, R.; Gautam, R. Light absorbing impurity deposition over the Himalayan-Karakoram-Hindu Kush-Tibetan cryosphere: A review and satellite-based characterization. L. Surf. Cryosph. Remote Sens. III 2016. [Google Scholar] [CrossRef]
- Li, C.; Bosch, C.; Kang, S.; Andersson, A.; Chen, P.; Zhang, Q.; Cong, Z.; Chen, B.; Qin, D.; Gustafsson, Ö. Sources of black carbon to the Himalayan-Tibetan Plateau glaciers. Nat. Commun. 2016, 7, 1–7. [Google Scholar] [CrossRef]
- Wu, K.; Liu, S.; Jiang, Z.; Xu, J.; Wei, J.; Guo, W. Recent glacier mass balance and area changes in the Kangri Karpo Mountains from DEMs and glacier inventories. Cryosphere 2018, 12, 103–121. [Google Scholar] [CrossRef] [Green Version]
- Qu, B.; Ming, J.; Kang, S.C.; Zhang, G.S.; Li, Y.W.; Li, C.D.; Zhao, S.Y.; Ji, Z.M.; Cao, J.J. The decreasing albedo of the Zhadang glacier on western Nyainqentanglha and the role of light-absorbing impurities. Atmos. Chem. Phys. 2014, 14, 11117–11128. [Google Scholar] [CrossRef] [Green Version]
- Kaab, A.; Treichler, D.; Nuth, C.; Berthier, E. Brief Communication: Contending estimates of 2003-2008 glacier mass balance over the Pamir-Karakoram-Himalaya. Cryosphere 2015, 9, 557–564. [Google Scholar] [CrossRef] [Green Version]
- Paul, F.; Bolch, T.; Kaab, A.; Nagler, T.; Nuth, C.; Scharrer, K.; Shepherd, A.; Strozzi, T.; Ticconi, F.; Bhambri, R.; et al. The glaciers climate change initiative: Methods for creating glacier area, elevation change and velocity products. Remote Sens. Environ. 2015, 162, 408–426. [Google Scholar] [CrossRef] [Green Version]
- Yu, W.S.; Yao, T.D.; Kang, S.C.; Pu, J.C.; Yang, W.; Gao, T.G.; Zhao, H.B.; Zhou, H.; Li, S.H.; Wang, W.C.; et al. Different region climate regimes and topography affect the changes in area and mass balance of glaciers on the north and south slopes of the same glacierized massif (the West Nyainqentanglha Range, Tibetan Plateau). J. Hydrol. 2013, 495, 64–73. [Google Scholar] [CrossRef]
- Bolch, T.; Yao, T.; Kang, S.; Buchroithner, M.F.; Scherer, D.; Maussion, F.; Huintjes, E.; Schneider, C. A glacier inventory for the western Nyainqentanglha Range and the Nam Co Basin, Tibet, and glacier changes 1976–2009. Cryosphere 2010, 4, 419–433. [Google Scholar] [CrossRef] [Green Version]
- Yao, T.D.; Li, Z.G.; Yang, W.; Guo, X.J.; Zhu, L.P.; Kang, S.C.; Wu, Y.H.; Yu, W.S. Glacial distribution and mass balance in the Yarlung Zangbo river and its influence on lakes. Chin. Sci. Bull. 2010. [Google Scholar] [CrossRef]
- Guo, W.Q.; Liu, S.Y.; Xu, L.; Wu, L.Z.; Shangguan, D.H.; Yao, X.J.; Wei, J.F.; Bao, W.J.; Yu, P.C.; Liu, Q.; et al. The second Chinese glacier inventory: Data, methods and results. J. Glaciol. 2015, 61, 357–372. [Google Scholar] [CrossRef] [Green Version]
- Wang, T.Y.; Zhang, G.; Li, D.R.; Tang, X.M.; Jiang, Y.H.; Pan, H.B.; Zhu, X.Y.; Fang, C. Geometric Accuracy Validation for ZY-3 Satellite Imagery. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1168–1171. [Google Scholar] [CrossRef]
- Ni, W.J.; Sun, G.Q.; Ranson, K.J.; Pang, Y.; Zhang, Z.Y.; Yao, W. Extraction of ground surface elevation from ZY-3 winter stereo imagery over deciduous forested areas. Remote Sens. Environ. 2015, 159, 194–202. [Google Scholar] [CrossRef]
- Zhou, P.; Tang, X.; Wang, Z.; Cao, N.; Wang, X. Vertical accuracy effect verification for satellite imagery with different GCPs. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1268–1272. [Google Scholar] [CrossRef]
- Bhardwaj, A.; Sam, L.; Martin-Torres, F.J.; Kumar, R. UAVs as remote sensing platform in glaciology: Present applications and future prospects. Remote Sens. Environ. 2016, 175, 196–204. [Google Scholar] [CrossRef]
- Berthier, E.; Schiefer, E.; Clarke, G.K.C.; Menounos, B.; Remy, F. Contribution of Alaskan glaciers to sea-level rise derived from satellite imagery. Nat. Geosci. 2010, 3, 92–95. [Google Scholar] [CrossRef] [Green Version]
- Berthier, E.; Arnaud, Y.; Baratoux, D.; Vincent, C.; Remy, F. Recent rapid thinning of the “Mer de Glace” glacier derived from satellite optical images. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef] [Green Version]
- King, O.; Quincey, D.J.; Carrivick, J.L.; Rowan, A. V Spatial variability in mass loss of glaciers in the Everest region, central Himalayas, between 2000 and 2015. Cryosphere 2017, 11, 407–426. [Google Scholar] [CrossRef] [Green Version]
- Nuth, C.; Kaab, A. Co-registration and bias corrections of satellite elevation data sets for quantifying glacier thickness change. Cryosphere 2011, 5, 271–290. [Google Scholar] [CrossRef] [Green Version]
- Pieczonka, T.; Bolch, T.; Wei, J.F.; Liu, S.Y. Heterogeneous mass loss of glaciers in the Aksu-Tarim Catchment (Central Tien Shan) revealed by 1976 KH-9 Hexagon and 2009 SPOT-5 stereo imagery. Remote Sens. Environ. 2013, 130, 233–244. [Google Scholar] [CrossRef] [Green Version]
- Hohle, J.; Hohle, M. Accuracy assessment of digital elevation models by means of robust statistical methods. ISPRS J. Photogramm. Remote Sens. 2009, 64, 398–406. [Google Scholar] [CrossRef] [Green Version]
- Neelmeijer, J.; Motagh, M.; Bookhagen, B. High-resolution digital elevation models from single-pass TanDEM-X interferometry over mountainous regions: A case study of Inylchek Glacier, Central Asia. ISPRS J. Photogramm. Remote Sens. 2017, 130, 108–121. [Google Scholar] [CrossRef] [Green Version]
- Ke, L.; Ding, X.; Zhang, L.; Hu, J.; Shum, C.K.; Lu, Z. Compiling a new glacier inventory for southeastern Qinghai-Tibet Plateau from Landsat and Palsar data. J. Glaciol. 2016, 62, 579–592. [Google Scholar] [CrossRef] [Green Version]
- Paul, F.; Barrand, N.E.; Baumann, S.; Berthier, E.; Bolch, T.; Casey, K.; Frey, H.; Joshi, S.P.; Konovalov, V.; Le Bris, R.; et al. On the accuracy of glacier outlines derived from remote-sensing data. Ann. Glaciol. 2013, 54, 171–182. [Google Scholar] [CrossRef] [Green Version]
- Dussaillant, I.; Berthier, E.; Brun, F.; Masiokas, M.; Hugonnet, R.; Favier, V.; Rabatel, A.; Pitte, P.; Ruiz, L. Two decades of glacier mass loss along the Andes. Nat. Geosci. 2019, 12, 802–808. [Google Scholar] [CrossRef]
- Huintjes, E.; Sauter, T.; Schroter, B.; Maussion, F.; Yang, W.; Kropaček, J.; Buchroithner, M.; Scherer, D.; Kang, S.; Schneider, C. Evaluation of a Coupled Snow and Energy Balance Model for Zhadang Glacier, Tibetan Plateau, Using Glaciological Measurements and Time-Lapse Photography. Arct. Antarct. Alp. Res. 2015, 47, 573–590. [Google Scholar] [CrossRef]
- Zhou, Y.S.; Li, Z.; Li, J. Slight glacier mass loss in the Karakoram region during the 1970s to 2000 revealed by KH-9 images and SRTM DEM. J. Glaciol. 2017, 63, 331–342. [Google Scholar] [CrossRef] [Green Version]
- Rignot, E.; Echelmeyer, K.; Krabill, W. Penetration depth of interferometric synthetic-aperture radar signals in snow and ice. Geophys. Res. Lett. 2001, 28, 3501–3504. [Google Scholar] [CrossRef] [Green Version]
- Dall, J.; Madsen, S.N.; Keller, K.; Forsberg, R. Topography and penetration of the greenland ice sheet measured with airborne SAR interferometry. Geophys. Res. Lett. 2001, 28, 1703–1706. [Google Scholar] [CrossRef]
- Zhang, G.S.; Kang, S.C.; Fujita, K.; Huintjes, E.; Xu, J.Q.; Yamazaki, T.; Haginoya, S.; Wei, Y.; Scherer, D.; Schneider, C.; et al. Energy and mass balance of Zhadang glacier surface, central Tibetan Plateau. J. Glaciol. 2013, 59, 137–148. [Google Scholar] [CrossRef] [Green Version]
- Yang, W.; Yao, T.D.; Xu, B.Q.; Wu, G.J.; Ma, L.L.; Xin, X.D. Quick ice mass loss and abrupt retreat of the maritime glaciers in the Kangri Karpo Mountains, southeast Tibetan Plateau. Chin. Sci. Bull. 2008, 53, 2547–2551. [Google Scholar] [CrossRef] [Green Version]
- Huss, M. Density assumptions for converting geodetic glacier volume change to mass change. Cryosphere 2013, 7, 877–887. [Google Scholar] [CrossRef] [Green Version]
- Shangguan, D.H.; Bolch, T.; Ding, Y.J.; Krohnert, M.; Pieczonka, T.; Wetzel, H.U.; Liu, S.Y. Mass changes of Southern and Northern Inylchek Glacier, Central Tian Shan, Kyrgyzstan, during similar to 1975 and 2007 derived from remote sensing data. Cryosphere 2015, 9, 703–717. [Google Scholar] [CrossRef] [Green Version]
- Koblet, T.; Gartner-Roer, I.; Zemp, M.; Jansson, P.; Thee, P.; Haeberli, W.; Holmlund, P. Reanalysis of multi-temporal aerial images of Storglaciaren, Sweden (1959–99)—Part 1: Determination of length, area, and volume changes. Cryosphere 2010, 4, 333–343. [Google Scholar] [CrossRef] [Green Version]
- Neckel, N.; Braun, A.; Kropacek, J.; Hochschild, V. Recent mass balance of the Purogangri Ice Cap, central Tibetan Plateau, by means of differential X-band SAR interferometry. Cryosphere 2013, 7, 1623–1633. [Google Scholar] [CrossRef] [Green Version]
- Xu, K.; Jiang, Y.; Zhang, G.; Zhang, Q.; Wang, X. Geometric potential assessment for ZY3-02 triple linear array imagery. Remote Sens. 2017, 9, 658. [Google Scholar] [CrossRef] [Green Version]
- Grohmann, C.H. Evaluation of TanDEM-X DEMs on selected Brazilian sites: Comparison with SRTM, ASTER GDEM and ALOS AW3D30. Remote Sens. Environ. 2018, 212, 121–133. [Google Scholar] [CrossRef] [Green Version]
- Neckel, N.; Loibl, D.; Rankl, M. Recent slowdown and thinning of debris-covered glaciers in south-eastern Tibet. Earth Planet. Sci. Lett. 2017, 464, 95–102. [Google Scholar] [CrossRef] [Green Version]
- Huang, L.; Li, Z.; Han, H.; Tian, B.; Zhou, J. Analysis of thickness changes and the associated driving factors on a debris-covered glacier in the Tienshan Mountain. Remote Sens. Environ. 2018. [Google Scholar] [CrossRef]
- Cuffey, K.M.; Paterson, W.S.B. The Physics of Glaciers, 4th ed.; Elsevier: Burlington, MA, USA, 2010; ISBN 9780123694614. [Google Scholar]
- Muller, J.; Vieli, A.; Gartner-Roer, I. Rock glaciers on the run-understanding rock glacier landform evolution and recent changes from numerical flow modeling. Cryosphere 2016, 10, 2865–2886. [Google Scholar] [CrossRef] [Green Version]
- Lin, L.; Jiang, L.; Sun, Y.; Yi, C.; Wang, H.; Hsu, H. Glacier elevation changes (2012–2016) of the Puruogangri Ice Field on the Tibetan Plateau derived from bi-temporal TanDEM-X InSAR data. Int. J. Remote Sens. 2016, 37, 5687–5707. [Google Scholar]
- Dehecq, A.; Millan, R.; Berthier, E.; Gourmelen, N.; Trouve, E.; Vionnet, V. Elevation Changes Inferred From TanDEM-X Data Over the Mont-Blanc Area: Impact of the X-Band Interferometric Bias. Ieee J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 3870–3882. [Google Scholar] [CrossRef] [Green Version]
- Zhang, G.S.; Kang, S.C.; Cuo, L.; Qu, B. Modeling hydrological process in a glacier basin on the central Tibetan Plateau with a distributed hydrology soil vegetation model. J. Geophys. Res. 2016, 121, 9521–9539. [Google Scholar] [CrossRef] [Green Version]
- Neckel, N.; Kropacek, J.; Bolch, T.; Hochschild, V. Glacier mass changes on the Tibetan Plateau 2003-2009 derived from ICESat laser altimetry measurements. Environ. Res. Lett. 2014, 9. [Google Scholar] [CrossRef]
- Gardner, A.S.; Moholdt, G.; Cogley, J.G.; Wouters, B.; Arendt, A.A.; Wahr, J.; Berthier, E.; Hock, R.; Pfeffer, W.T.; Kaser, G.; et al. A Reconciled Estimate of Glacier Contributions to Sea Level Rise: 2003 to 2009. Science 2013, 340, 852–857. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dai, L.Y.; Che, T.; Xie, H.J.; Wu, X.J. Estimation of Snow Depth over the Qinghai-Tibetan Plateau Based on AMSR-E and MODIS Data. Remote Sens. 2018, 10, 1989. [Google Scholar] [CrossRef] [Green Version]
















| Data Source | Time | Spatial Resolution (m) | Purpose | |
|---|---|---|---|---|
| ZY-3/TLA in the Western Nyainqentanglha Mountains (WNM) | 2017/01/22 2013/12/03 | Nadir (2.5) Forward (3.5) Backward (3.5) | Calculate glacier surface elevation in WNM | |
| ZY-3/TLA in the Eastern Nyainqentanglha Mountains (ENM) | 2017/12/04 2013/03/09 | Calculate glacier surface elevation in ENM | ||
| Glacier Elevation Change Maps in the WNM and ENM [9,31] | 2000–2014 | 10 | Cross-validate the ZY-3 result and estimate X-band SAR signal penetration depth into glacier surface | |
| C-band Digital Elevation Model of Shuttle Radar Topography Mission (SRTM-C DEM) | 2000/02 | 30 | Reference elevation both on glacier surface in 2000 and in off-glacier region | |
| X-band Digital Elevation Model of Shuttle Radar Topography Mission (SRTM-X DEM) | 2000/02 | 30 | Estimate C-band SAR signal penetration depth | |
| Landsat Thematic Mapper (TM) | 2000–2017 | 30 | Classify the clean ice and debris-covered glacier | |
| ID | Number of GCPs | Number of ECPs | RMSE (pixel) | RMSE (m) | ||
|---|---|---|---|---|---|---|
| x | y | z | ||||
| 2017NBENM | 15 | 986 | 0.50 | 1.77 | 2.46 | 1.05 |
| 2017NFENM | 0.53 | 1.91 | 2.21 | 1.07 | ||
| 2017BFENM | 0.70 | 1.23 | 1.90 | 2.25 | ||
| 2013NBENM | 13 | 855 | 0.49 | 1.85 | 1.22 | 1.01 |
| 2013NFENM | 0.50 | 1.56 | 0.99 | 1.04 | ||
| 2013BFENM | 0.63 | 1.51 | 1.28 | 2.02 | ||
| 2017NBWNM | 10 | 2159 | 0.29 | 1.03 | 1.82 | 0.59 |
| 2017NFWNM | 0.28 | 0.92 | 1.57 | 0.59 | ||
| 2017BFWNM | 0.42 | 1.12 | 1.99 | 1.36 | ||
| 2013NBWNM | 10 | 2066 | 0.28 | 1.77 | 2.26 | 0.58 |
| 2013NFWNM | 0.27 | 1.8 | 1.89 | 0.55 | ||
| 2013BFWNM | 0.40 | 1.56 | 1.99 | 1.30 | ||
| Mean | 0.44 | 1.50 | 1.80 | 1.12 | ||
| ID | Co-Registration Shift (m) | Basic Statistics on Elevation Difference between ZY-3 DEMs and SRTM-C DEM | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Before Correction | After Correction | Change in σ (%) after Correction | Change in NMAD (%) after Correction | ||||||
| x | y | z | Mean ± σ | Median ± NMAD | Mean ± σ | Median ± NMAD | |||
| 2017NBENM | 3.65 | 2.06 | 1.40 | −2.12 ± 9.76 | −2.29 ± 8.96 | −0.72 ± 9.76 | −0.89 ± 8.96 | 0.01 | 0.01 |
| 2017NFENM | 4.46 | 1.84 | 6.46 | −6.76 ± 9.94 | −6.92 ± 9.19 | −0.23 ± 9.42 | −0.40 ± 8.67 | −5.19 | −5.64 |
| 2017BFENM | 6.25 | 1.88 | 5.30 | −4.61 ± 8.81 | −4.71 ± 8.04 | −0.19 ± 8.49 | −0.10 ± 7.72 | −3.69 | −4.07 |
| 2013NBENM | 3.39 | 5.47 | −0.48 | 0.48 ± 11.98 | 0.47 ± 10.88 | −0.37 ± 12.07 | −0.42 ± 10.96 | 0.73 | 0.70 |
| 2013NFENM | 1.89 | 3.25 | 3.73 | −4.14 ± 12.83 | −4.18 ± 11.75 | −0.63 ± 12.07 | −0.74 ± 11.00 | −5.91 | −6.40 |
| 2013BFENM | 5.27 | 5.29 | 2.86 | −1.39 ± 9.80 | −1.48 ± 8.86 | 0.35 ± 9.24 | 0.44 ± 8.28 | −5.63 | −6.45 |
| 2017NBWNM | 0.88 | 5.47 | 2.31 | −1.74 ± 8.52 | −1.78 ± 5.17 | 0.35 ± 8.50 | 0.33 ± 5.15 | −0.22 | −0.27 |
| 2017NFWNM | 0.68 | 1.70 | 6.63 | −6.91 ± 8.68 | −6.68 ± 5.43 | −0.49 ± 8.49 | −0.3 ± 5.32 | −2.19 | −1.85 |
| 2017BFWNM | 1.29 | 9.02 | 4.51 | −3.87 ± 9.19 | −3.92 ± 5.65 | −0.06 ± 8.68 | 0.02 ± 5.31 | −5.52 | −5.96 |
| 2013NBWNM | 3.05 | 8.74 | 2.72 | −1.96 ± 7.59 | −1.98 ± 4.71 | 0.41 ± 7.67 | 0.37 ± 4.84 | 1.09 | 2.80 |
| 2013NFWNM | −1.43 | 9.48 | 6.79 | −6.81 ± 7.68 | −6.57 ± 4.93 | −0.35 ± 7.33 | −0.19 ± 4.64 | −4.50 | −5.92 |
| 2013BFWNM | −0.81 | 12.26 | 4.76 | −4.01 ± 8.01 | −4.01 ± 5.14 | −0.24 ± 7.58 | −0.07 ± 4.74 | −5.35 | −7.80 |
| ID | Mean Point Distance (m) | Improvement in Distance | Percentage of Valid Data (%) | Improvement in Valid Data (%) | ||
|---|---|---|---|---|---|---|
| Before Fusion | After Fusion | Before Fusion | After Fusion | |||
| 2017NBENM | 5.05 | 3.09 | −1.96 | 65.94% | 92.75% | 26.82% |
| 2017NFENM | 4.24 | −1.15 | 88.48% | 4.27% | ||
| 2017BFENM | 9.96 | −6.86 | 37.55% | 55.20% | ||
| 2013NBENM | 7.74 | 4.89 | −2.85 | 34.82% | 54.66% | 19.84% |
| 2013NFENM | 6.82 | −1.93 | 44.36% | 10.30% | ||
| 2013BFENM | 15.53 | −10.64 | 17.96% | 36.70% | ||
| 2017NBWNM | 5.98 | 3.79 | −2.19 | 68.15% | 85.46% | 17.31% |
| 2017NFWNM | 5.63 | −1.84 | 74.99% | 10.47% | ||
| 2017BFWNM | 11.38 | −7.59 | 43.51% | 41.95% | ||
| 2013NBWNM | 5.86 | 3.90 | −1.96 | 74.85% | 91.62% | 16.77% |
| 2013NFWNM | 5.51 | −1.61 | 82.57% | 9.05% | ||
| 2013BFWNM | 10.90 | −7.00 | 48.67% | 42.95% | ||
| Average | 7.88 | 3.92 | −3.96 | 56.82% | 81.12% | 24.30% |
| Acquisition | Ms (m) | δs (m) | Median (m) | NMAD (m) | N | Neff | δe (m) | δmb (m w.e.) |
|---|---|---|---|---|---|---|---|---|
| 2013WNM − SRTM | 0.97 | 7.12 | 1.04 | 4.28 | 81,654,768 | 2,041,369 | 0.97 | 0.23 |
| 2017WNM − 2013WNM | 0.03 | 3.04 | 0.10 | 3.01 | 67,949,809 | 1,698,745 | 0.03 | 0.06 |
| 2017WNM − SRTM | 0.80 | 8.06 | 0.86 | 4.73 | 68,836,853 | 1,720,921 | 0.80 | 0.19 |
| 2013ENM − SRTM | −0.41 | 11.12 | −0.52 | 10.07 | 56,358,788 | 1,408,970 | 0.41 | / |
| 2017ENM − 2013ENM | −0.18 | 5.95 | −0.29 | 4.95 | 47,187,872 | 1,179,697 | 0.18 | / |
| 2017ENM − SRTM | −0.55 | 8.79 | −0.74 | 8.00 | 62,405,134 | 1,560,128 | 0.55 | 0.20 |
| Region | WNM (m w.e. a−1) | ENM (m w.e. a−1) | |||||
|---|---|---|---|---|---|---|---|
| Area (km2) | 2000−2013 | 2013−2017 | RC (%) | 2000−2017 | Area (km2) | 2000−2017 | |
| Ablation region | 269.95 | −0.50 ± 0.23 | −0.64 ± 0.06 | 26.8 | −0.55 ± 0.19 | 403.47 | −0.77 ± 0.20 |
| Accumulation region | 201.32 | 0.17 ± 0.23 | −0.16 ± 0.06 | 192.3 | 0.05 ± 0.19 | 148.98 | 1 0.005 ± 0.20 |
| Inside Nam Co basin | 108.59 | −0.28 ± 0.23 | −0.46 ± 0.06 | 65.6 | −0.32 ± 0.19 | ||
| Outside Nam Co basin | 362.68 | −0.20 ± 0.23 | −0.41 ± 0.06 | 106.7 | −0.29 ± 0.19 | ||
| 5O282B basin | 197.23 | −0.52 ± 0.20 | |||||
| 5O291B basin | 355.21 | −0.57 ± 0.20 | |||||
| Total | 471.27 | −0.22 ± 0.23 | −0.43 ± 0.06 | 101.8 | −0.30 ± 0.19 | 552.44 | −0.56 ± 0.20 |
| Glacier Name | GLIMs ID | Region | Elevation of Mixed Region (m) | Area (km2) | Surface Elevation Changes (m a−1) | |
|---|---|---|---|---|---|---|
| 2000−2013 | 2013−2017 | |||||
| Un−named | G090388E30292N | Debris-covered | 5400–5800 | 0.64 | −0.90 | −0.51 |
| Clean-ice | 2.32 | −0.62 | −0.46 | |||
| Xibu | G090598E30389N | Debris-covered | 5150−5600 | 3.22 | −0.81 | / |
| Clean-ice | 3.53 | −0.54 | / | |||
| Azha | G096818E29132N | Debris-covered | 2400−3750 | 3.01 | −3.40 | −3.65 |
| Clean-ice | 6.41 | −1.58 | −4.90 | |||
| Xueyougu | G096758E29147N | Debris-covered | 3000−3300 | 0.96 | −1.53 | −3.25 |
| Clean-ice | 1.25 | −0.98 | −3.54 | |||
| Region | Study | Data | Period | Mass Balance (m w.e. a−1) |
|---|---|---|---|---|
| Zhadang | Yu et al. [35] | In-situ | 2005−2008 | −0.59 |
| Zhang et al. [57] | In−situ | 2009−2011 | −1.20 | |
| Zhang et al. [71] | In−situ | 2011−2014 | −1.60 | |
| Li et al. [9] | TerraSAR-X/TanDEM-X | 2000−2014 | −0.501 ± 0.166 | |
| This study | ZY-3 TLA | 2000−2017 | −0.60 ±0.19 | |
| Gurenhekou | Yao et al. [5] | In-situ | 2005−2010 | −0.31 |
| Yu et al. [37] | In-situ | 2004−2005 | −0.4 | |
| Li et al. [9] | TerraSAR-X/TanDEM-X | 2000−2014 | −0.267 ± 0.248 | |
| This study | ZY-3 TLA | 2000−2017 | −0.40 ± 0.19 | |
| Western Nyainqentanglha Mountains | Yao et al. [5] | In-situ | 2005−2010 | −0.2 |
| Neckel et al. [72] | 1ICESat/GLAS | 2003−2009 | −0.20 ± 0.29 | |
| Li et al. [9] | TerraSAR-X/TanDEM-X | 2000−2014 | −0.235 ± 0.127 | |
| 2Brun et al. [13] | ASTER Stereo Image | 2000−2016 | −0.35 ± 0.07 | |
| Zhou et al. [3] | KH−9 | 1975−2000 | −0.25 ± 0.15 | |
| This study | ZY-3 TLA | 2000−2013 | −0.22 ± 0.23 | |
| 2013−2017 | −0.43 ± 0.06 | |||
| 2000−2017 | −0.30 ± 0.19 |
| Region | Study | Data | Period | Mass Balance(m w.e. a−1) |
|---|---|---|---|---|
| Parlung No.4 | Yang et al. [58] | In-situ | 2006−2007 | −0.71 |
| Wu et al. [31] | TerraSAR-X/TanDEM-X | 2000−2014 | −0.61 ± 0.22 | |
| This Study | ZY-3 TLA | 2000−2017 | −0.54 ± 0.20 | |
| Eestern Nyainqentanglha Mountains (ENM) | Yao et al. [5] | In-situ | 2005−2010 | −1.1 |
| Gardner et al. [7] | SPOT Stereo Image | 2000−2011 | −0.33 ± 0.14 | |
| Gardner et al. [73] | ICESat/GLAS | 2003−2009 | −0.26 ± 0.11 | |
| Neckel et al. [72] | ICESat/GLAS | 2003−2009 | −0.69 ± 0.36 | |
| Kääb et al. [33] | ICESat/GLAS | 2003−2009 | −1.14 ± 0.25 | |
| Phan et al. [34] | ICESat/GLAS | 2003−2009 | −0.57± 0.49 | |
| 1Brun et al. [13] | ASTER Stereo Image | 2000−2016 | −0.75 ± 0.23 | |
| Wu et al. [31] | TerraSAR-X/TanDEM-X | 2000−2014 | −0.67 ± 0.09 | |
| Zhou et al. [3] | KH−9 | 1975−2000 | −0.19 ± 0.14 | |
| This Study | ZY-3 TLA | 2000−2017 | −0.56 ± 0.20 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, S.; Menenti, M.; Jia, L.; Zhang, J.; Zhang, J.; Li, X. Glacier Mass Balance in the Nyainqentanglha Mountains between 2000 and 2017 Retrieved from ZiYuan-3 Stereo Images and the SRTM DEM. Remote Sens. 2020, 12, 864. https://doi.org/10.3390/rs12050864
Ren S, Menenti M, Jia L, Zhang J, Zhang J, Li X. Glacier Mass Balance in the Nyainqentanglha Mountains between 2000 and 2017 Retrieved from ZiYuan-3 Stereo Images and the SRTM DEM. Remote Sensing. 2020; 12(5):864. https://doi.org/10.3390/rs12050864
Chicago/Turabian StyleRen, Shaoting, Massimo Menenti, Li Jia, Jing Zhang, Jingxiao Zhang, and Xin Li. 2020. "Glacier Mass Balance in the Nyainqentanglha Mountains between 2000 and 2017 Retrieved from ZiYuan-3 Stereo Images and the SRTM DEM" Remote Sensing 12, no. 5: 864. https://doi.org/10.3390/rs12050864
APA StyleRen, S., Menenti, M., Jia, L., Zhang, J., Zhang, J., & Li, X. (2020). Glacier Mass Balance in the Nyainqentanglha Mountains between 2000 and 2017 Retrieved from ZiYuan-3 Stereo Images and the SRTM DEM. Remote Sensing, 12(5), 864. https://doi.org/10.3390/rs12050864