Variability of Kuroshio Surface Axis Northeast of Taiwan Island Derived from Satellite Altimeter Data
Abstract
:1. Introduction
2. Data and Methods
2.1. Data
2.2. Methods
2.2.1. Extraction Method for Kuroshio Surface Axis
2.2.2. Empirical Mode Decomposition
2.2.3. Self-Organizing Map Analysis
3. Results and Discussion
3.1. General Features of the Kuroshio Mean Axis
3.2. Variation of the Kuroshio Surface Axis
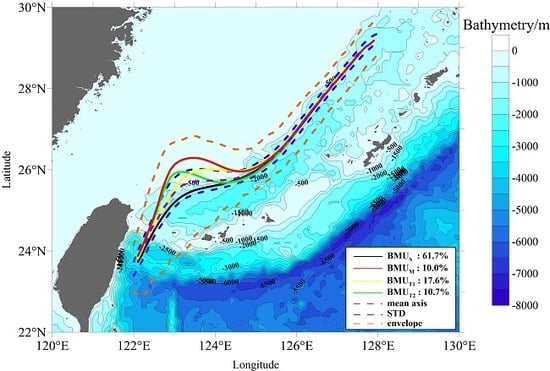
3.3. Self-Organizing Map Analysis
3.4. Impact of Mesoscale Eddies on the Kuroshio Surface Axis Variability
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A

References
- Qiu, B. Kuroshio and Oyashio currents. In Encyclopedia of Ocean Sciences; Steele, J.H., Turekian, K.K., Thorpe, S.A., Eds.; Academic Press: New York, NY, USA, 2001; Volume 6, pp. 1413–1425. [Google Scholar]
- Su, J.; Pan, Y. On the shelf circulation north of Taiwan. Acta Oceanol. Sin. 1987, 6, 1–20. [Google Scholar]
- Tang, T.Y.; Tai, J.H.; Yang, Y.J. The flow pattern north of Taiwan and the migration of the Kuroshio. Cont. Shelf Res. 2000, 20, 349–371. [Google Scholar] [CrossRef]
- Isobe, A. Recent advances in ocean-circulation research on the Yellow Sea and East China Sea shelves. J. Oceanogr. 2008, 64, 569–584. [Google Scholar] [CrossRef]
- Sun, X.P.; Su, Y.F. On the variation of Kuroshio in East China Sea. In Oceanology of China Seas; Zhou, D., Liang, Y., Zeng, C., Eds.; Kluwer Academic: Dordrecht, The Netherlands, 1994; Volume 1, pp. 49–58. [Google Scholar]
- Hu, X.; Xiong, X.; Qiao, F.; Guo, B.; Lin, X. Surface current field and seasonal variability in the Kuroshio and adjacent regions derived from satellite-tracked drifter data. Acta Oceanol. Sin. 2008, 3, 11–29. [Google Scholar]
- Qiu, B.; Imasato, N. A numerical study on the formation of the Kuroshio Counter Current and the Kuroshio Branch Current in the East China Sea. Cont. Shelf Res. 1990, 10, 165–184. [Google Scholar] [CrossRef]
- Tang, T.Y.; Hsueh, Y.; Yang, Y.J.; Ma, J.C. Continental slope flow northeast of Taiwan. J. Phys. Oceanogr. 1999, 29, 1353–1362. [Google Scholar] [CrossRef]
- Liu, Z.; Gan, J. Variability of the Kuroshio in the East China Sea derived from satellite altimetry data. Deep Sea Res. Part I 2012, 59, 25–36. [Google Scholar] [CrossRef]
- Zhou, P.; Song, X.; Yuan, Y.; Wang, W.; Yu, Z. Intrusion pattern of the Kuroshio Subsurface Water onto the East China Sea continental shelf traced by dissolved inorganic iodine species during the spring and autumn of 2014. Mar. Chem. 2017, 196, 24–34. [Google Scholar] [CrossRef]
- Nitani, H. Beginning of the Kuroshio. In Kuroshio, Physical Aspects of the Japan Current; Stommel, H., Yoshida, K., Eds.; University of Washington Press: Seattle, WA, USA, 1972; pp. 129–163. [Google Scholar]
- Teague, W.J.; Jacobs, G.A.; Ko, D.S.; Tang, T.Y.; Chang, K.I.; Suk, M.S. Connectivity of the Taiwan, Cheju, and Korea Straits. Cont. Shelf Res. 2003, 13, 63–77. [Google Scholar] [CrossRef]
- Lee, J.S.; Matsuno, T. Intrusion of Kuroshio water onto the continental shelf of the East China Sea. J. Oceanogr. 2007, 63, 309–325. [Google Scholar] [CrossRef]
- Chang, Y.L.; Oey, L.Y. Interannual and seasonal variations of Kuroshio transport east of Taiwan inferred from 29 years of tidegauge data. Geophys. Res. Lett. 2011, 38, L08603. [Google Scholar] [CrossRef]
- Soeyanto, E.X.; Guo, J.; Miyazawa, Y. Interannual variations of Kuroshio transport in the East China Sea and its relation to the Pacific Decadal Oscillation and mesoscale eddies. J. Geophys. Res. Ocean. 2014, 119, 3595–3616. [Google Scholar] [CrossRef]
- Delman, A.S.; McClean, J.L.; Sprintall, J.; Talley, L.D.; Yulaeva, E.; Jayne, S.R. Effects of eddy vorticity forcing on the mean state of the Kuroshio Extension. J. Phys. Oceanogr. 2015, 45, 1356–1375. [Google Scholar] [CrossRef]
- Ichikawa, K.; Tokeshi, R.; Kashima, M.; Sato, K.; Matsuoka, T.; Kojima, S.; Fujii, S. Kuroshio variations in the upstream region as seen by HF radar and satellite altimetry data. Int. J. Remote Sens. 2008, 29, 6417–6426. [Google Scholar] [CrossRef]
- Gawarkiewicz, G.; Jan, S.; Lermusiaux, P.F.; McClean, J.L.; Centurioni, L.; Taylor, K.; Sanford, T. Circulation and intrusions northeast of Taiwan: Chasing and predicting uncertainty in the cold dome. Oceanography 2011, 24, 110–121. [Google Scholar] [CrossRef]
- Velez-Belchi, P.; Centurioni, L.R.; Lee, D.-K.; Jan, S.; Niiler, P.P. Eddy induced Kuroshio intrusions onto the continental shelf of the East China Sea. J. Mar. Res. 2013, 71, 83–107. [Google Scholar] [CrossRef]
- Yin, Y.; Lin, X.; He, R.; Hou, Y. Impact of mesoscale eddies on Kuroshio intrusion variability northeast of Taiwan. J. Geophys. Res. Ocean. 2017, 122, 3021–3040. [Google Scholar] [CrossRef]
- Arbic, B.K.; Scott, R.B.; Chelton, D.B.; Richman, J.G.; Shriver, J.F. Effects of stencil width on surface ocean geostrophic velocity and vorticity estimation from gridded satellite altimeter data. J. Geophys. Res. Ocean. 2012, 117, 1–18. [Google Scholar] [CrossRef] [Green Version]
- CNES. SSALTO/DUACS Experimental Product Handbook. 2019. Available online: https://www.aviso.altimetry.fr/en/data/product-information/aviso-user-handbooks.html (accessed on 1 March 2020).
- Ambe, D.; Imawaki, S.; Uchida, H.; Ichikawa, K. Estimating the Kuroshio axis south of Japan using combination of satellite altimetry and drifting buoys. J. Oceanogr. 2004, 60, 375–382. [Google Scholar] [CrossRef]
- Cheng, K.H.; Lin, C.C.; Hsu, P.C.; Huang, S.J. Reconstruction and analysis of surface velocity from drifters in the Kuroshio region east of Taiwan. J. Mar. Sci. Technol. 2016, 24, 1217–1225. [Google Scholar]
- Yang, J.; Zhang, J.; Cui, W.; Zhao, X.; Han, W.; Martinez, B. Validation, analysis of the Chinese HY-2 satellite altimeter data and their applications in the China Sea and its vicinity. In Proceedings of the Dragon 3 Final Results and Dragon 4 Kick-Off Symposium, Wuhan, China, 4–8 July 2016; Volume 739. [Google Scholar]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. Math. Phys. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Ho, C.R.; Zheng, Q.; Kuo, N.J.; Tsai, C.H.; Huang, N.E. Observation of the Kuroshio intrusion region in the South China Sea from AVHRR data. Int. J. Remote Sens. 2004, 25, 4583–4591. [Google Scholar] [CrossRef]
- Zhang, W.; Zhuang, X.; Chen, C.A.; Huang, T. The impact of Kuroshio water on the source water of the southeastern Taiwan Strait: Numerical results. Acta Oceanol. Sin. 2015, 34, 23–34. [Google Scholar] [CrossRef]
- Wu, C.R.; Wang, Y.L.; Lin, Y.F.; Chiang, T.L.; Wu, C.C. Weakening of the Kuroshio intrusion into the South China Sea under the global warming hiatus. IEEE J. STARS 2016, 9, 5064–5070. [Google Scholar] [CrossRef]
- Kohonen, T. Self-organized formation of topologically correct feature maps. Biol. Cybern. 1982, 43, 59–69. [Google Scholar] [CrossRef]
- Yin, Y.; Lin, X.; Li, Y.; Zeng, X. Seasonal variability of Kuroshio intrusion northeast of Taiwan Island as revealed by self-organizing map. Chin. J. Oceanol. Limnol. 2014, 32, 1435–1442. [Google Scholar] [CrossRef]
- Liu, Y.; Weisberg, R.H.; Yuan, Y. Patterns of upper layer circulation variability in the South China Sea from satellite altimetry using the self-organizing map. Acta Oceanol. Sin. 2008, 27, 129–144. [Google Scholar]
- Zeng, X.; He, R. Gulf Stream variability and a triggering mechanism of its large meander in the South Atlantic Bight. J. Geophys. Res. Ocean. 2016, 121, 8021–8038. [Google Scholar] [CrossRef]
- Jin, B.; Wang, G.; Liu, Y.; Zhang, R. Interaction between the East China Sea Kuroshio and the Ryukyu Current as revealed by the self-organizing map. J. Geophys. Res. Ocean. 2010, 115, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Tsui, I.F.; Wu, C.R. Variability analysis of Kuroshio intrusion through Luzon Strait using growing hierarchical self-organizing map. Ocean Dyn. 2012, 62, 1187–1194. [Google Scholar] [CrossRef]
- Beale, M.H.; Hagan, M.T.; Demuth, H.B. Neural Network Toolbox™ User’s Guide; The MathWorks Inc.: Natick, MA, USA, 2010; pp. 267–310. [Google Scholar]
- Vesanto, J.; Alhoniemi, E. Clustering of the self-organizing map. IEEE Trans. Neural Netw. 2000, 11, 586–600. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Weisberg, R.H.; Mooers, C.N.K. Performance evaluation of the self-organizing map for feature extraction. J. Geophys. Res. 2006, 111, C05018. [Google Scholar] [CrossRef]
- Daqrouq, K.; Al-Qawasmi, A.; Daoud, O.; Al-Sawalmeh, W. Self-organizing map weights and wavelet packet entropy for speaker verification. Int. J. Circ. Syst. Signal Process. 2012, 6, 12–20. [Google Scholar]
- Zhu, C. Unified entropy in self-organizing feature maps neural network. In Proceedings of the 2017 2nd International Symposium on Advances in Electrical, Electronics and Computer Engineering (ISAEECE 2017), Shanghai, China, 25–26 March 2017; Volume 124. [Google Scholar]
- Chamundeswari, G.; Varma, G.P.S.; Satyanarayana, C. An edge based clustering technique with self-organizing maps. Inf. Technol. Comput. Sci. 2018, 5, 30–39. [Google Scholar] [CrossRef]
- Alikhani, M.; Nedaie, A.; Ahmadvand, A. Presentation of clustering-classification heuristic method for improvement accuracy in classification of severity of road accidents in Iran. Saf. Sci. 2013, 60, 142–150. [Google Scholar] [CrossRef]
- Kalteh, A.M.; Hjorth, P.; Berndtsson, R. Review of the self-organizing map (SOM) approach in water resources: Analysis, modelling and application. Environ. Modell. Softw. 2008, 23, 835–845. [Google Scholar] [CrossRef]
- Matić, F.; Kalinić, H.; Vilibić, I. Interpreting self-organizing map errors in the classification of ocean patterns. Comput. Geosci. 2018, 119, 9–17. [Google Scholar] [CrossRef]
- Guan, B. Variability of Kuroshio in the East China Sea. Oceanol. Limnol. Sin. 1979, 10, 297–306. [Google Scholar]
- Hsueh, Y.; Wang, J.; Chern, C.S. The intrusion of the Kuroshio across the continental shelf northeast of Taiwan. J. Geophys. Res. Ocean. 1992, 97, 14323–14330. [Google Scholar] [CrossRef]
- De Bodt, E.; Cottrell, M.; Verleysen, M. Statistical tools to assess the reliability of Self-Organizing Maps. Neural Netw. 2002, 15, 967–978. [Google Scholar] [CrossRef] [Green Version]
- Wold, S.; Esbensen, K.; Geladi, P. Principal component analysis. Chemom. Intell. Lab. Syst. 1987, 2, 37–52. [Google Scholar] [CrossRef]
- Kim, K. Face recognition using principle component analysis. In Proceedings of the International Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 25–29 August 1996; Volume 586. [Google Scholar]
- Oey, L.Y.; Hsin, Y.C.; Wu, C.R. Why does the Kuroshio northeast of Taiwan shift shelfward in winter? Ocean Dyn. 2010, 60, 413–426. [Google Scholar] [CrossRef]
- Wu, C.R.; Hsin, Y.C.; Chiang, T.L.; Lin, Y.F.; Tsui, I.F. Seasonal and interannual changes of the Kuroshio intrusion onto the East China Sea Shelf. J. Geophys. Res. Ocean. 2014, 119, 5039–5051. [Google Scholar] [CrossRef]
- Liang, X.S.; Su, J.L. A two-layer model for the circulation in the East China Sea. Acta Oceanol. Sin. 1994, 13, 45–72. [Google Scholar]
- Vallis, G.K. Atmospheric and Oceanic Fluid Dynamics: Fundamentals and Large-Scale Circulation; Cambridge University Press: Cambridge, UK, 2006; pp. 178–188. [Google Scholar]

















© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhuang, Z.; Zheng, Q.; Zhang, X.; Yang, G.; Zhao, X.; Cao, L.; Zhang, T.; Yuan, Y. Variability of Kuroshio Surface Axis Northeast of Taiwan Island Derived from Satellite Altimeter Data. Remote Sens. 2020, 12, 1059. https://doi.org/10.3390/rs12071059
Zhuang Z, Zheng Q, Zhang X, Yang G, Zhao X, Cao L, Zhang T, Yuan Y. Variability of Kuroshio Surface Axis Northeast of Taiwan Island Derived from Satellite Altimeter Data. Remote Sensing. 2020; 12(7):1059. https://doi.org/10.3390/rs12071059
Chicago/Turabian StyleZhuang, Zhanpeng, Quanan Zheng, Xi Zhang, Guangbing Yang, Xinhua Zhao, Lei Cao, Ting Zhang, and Yeli Yuan. 2020. "Variability of Kuroshio Surface Axis Northeast of Taiwan Island Derived from Satellite Altimeter Data" Remote Sensing 12, no. 7: 1059. https://doi.org/10.3390/rs12071059
APA StyleZhuang, Z., Zheng, Q., Zhang, X., Yang, G., Zhao, X., Cao, L., Zhang, T., & Yuan, Y. (2020). Variability of Kuroshio Surface Axis Northeast of Taiwan Island Derived from Satellite Altimeter Data. Remote Sensing, 12(7), 1059. https://doi.org/10.3390/rs12071059