Figure 1.
Relative errors of the two-stream model as a function of the gas optical depth () for the O2 A-band (red) and CO2 band (blue). Left panel corresponds to the ‘Aerosol 1’ scenario, while right panel shows the results for the ‘Cloud 1’ scenario. Note that left Y axis refer to CO2 while right Y axis refer to O2 A-band.
Figure 1.
Relative errors of the two-stream model as a function of the gas optical depth () for the O2 A-band (red) and CO2 band (blue). Left panel corresponds to the ‘Aerosol 1’ scenario, while right panel shows the results for the ‘Cloud 1’ scenario. Note that left Y axis refer to CO2 while right Y axis refer to O2 A-band.
Figure 2.
Spectral radiances for the ‘Aerosol 2’ scenario computed by using the multi-stream (black), the two-stream (gray) and the single-scattering (light gray) RTMs: (upper panel) O2 A-band, (lower panel) CO2 band.
Figure 2.
Spectral radiances for the ‘Aerosol 2’ scenario computed by using the multi-stream (black), the two-stream (gray) and the single-scattering (light gray) RTMs: (upper panel) O2 A-band, (lower panel) CO2 band.
Figure 3.
Radiance computed with the multi-stream model as a function of radiances computed by using the low-stream models (two-stream and single-scattering models) for the O2 A- and CO2 bands. The figure corresponds to the ‘Aerosol 2’ scenario.
Figure 3.
Radiance computed with the multi-stream model as a function of radiances computed by using the low-stream models (two-stream and single-scattering models) for the O2 A- and CO2 bands. The figure corresponds to the ‘Aerosol 2’ scenario.
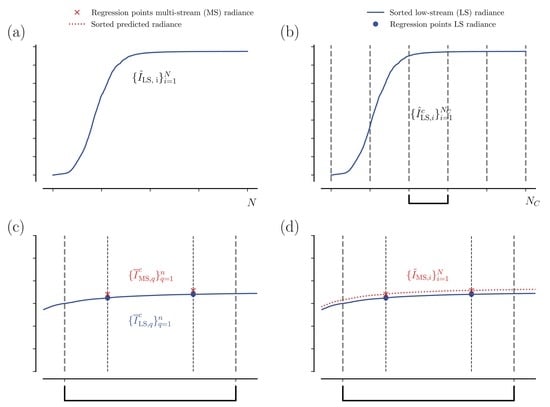
Figure 4.
Scheme of the Cluster Low-Streams Regression (CLSR) method. (a) Sorted radiance of the low-stream (LS) model in ascending order (blue line). (b) Division of the LS radiance in equal clusters C in the sorted domain. (c) Zoom for one cluster and the selected regression points of the multi-stream (MS) radiance (red crosses). (d) Reconstruction of the MS spectra: the predicted radiance is computed for all the spectral points (dashed red line).
Figure 4.
Scheme of the Cluster Low-Streams Regression (CLSR) method. (a) Sorted radiance of the low-stream (LS) model in ascending order (blue line). (b) Division of the LS radiance in equal clusters C in the sorted domain. (c) Zoom for one cluster and the selected regression points of the multi-stream (MS) radiance (red crosses). (d) Reconstruction of the MS spectra: the predicted radiance is computed for all the spectral points (dashed red line).
Figure 5.
Radiance spectra computed by using the multi-stream RTM for three atmospheric scenarios: ‘Clear sky’ (black), ‘Cloud 1’ (purple) and ‘Cloud 2’ (blue). The upper panel corresponds to the O2 A-band, while the bottom panel is for the CO2 weak band.
Figure 5.
Radiance spectra computed by using the multi-stream RTM for three atmospheric scenarios: ‘Clear sky’ (black), ‘Cloud 1’ (purple) and ‘Cloud 2’ (blue). The upper panel corresponds to the O2 A-band, while the bottom panel is for the CO2 weak band.
Figure 6.
Box plots of the residuals with respect to the continuum in percentage for (upper panels) the PCA model and (bottom panels) the CLSR method, when the low-stream model is (a) the two-stream model for the ‘Cloud 2’ scenario or (b) the single-scattering model for the ‘Aerosol 2’ scenario. The red boxes indicate the O2 A-band while the blue boxes indicate the CO2 band. Box description: the upper and lower limits of the box represent the interquartile range (IQR), which is () being the i-th quartile; the upper and lower whiskers indicate ( IQR) and ( IQR), respectively; the orange line inside the box represents the median; the orange values on top of each box indicate the median values and the black values correspond to the IQR value.
Figure 6.
Box plots of the residuals with respect to the continuum in percentage for (upper panels) the PCA model and (bottom panels) the CLSR method, when the low-stream model is (a) the two-stream model for the ‘Cloud 2’ scenario or (b) the single-scattering model for the ‘Aerosol 2’ scenario. The red boxes indicate the O2 A-band while the blue boxes indicate the CO2 band. Box description: the upper and lower limits of the box represent the interquartile range (IQR), which is () being the i-th quartile; the upper and lower whiskers indicate ( IQR) and ( IQR), respectively; the orange line inside the box represents the median; the orange values on top of each box indicate the median values and the black values correspond to the IQR value.
Figure 7.
Explained variance ratio in percentage as a function of the number of PCs for all the atmospheric scenarios: ‘Clear sky’, ‘Aerosol 1’, ‘Aerosol 2’, ‘Cloud 1’ and ‘Cloud 2’; and the two spectral bands (O2 A- and CO2 bands). The red color corresponds to the O2 A-band and the blue color to the CO2 weak band. The different dashing of the lines indicates the different atmospheric scenarios.
Figure 7.
Explained variance ratio in percentage as a function of the number of PCs for all the atmospheric scenarios: ‘Clear sky’, ‘Aerosol 1’, ‘Aerosol 2’, ‘Cloud 1’ and ‘Cloud 2’; and the two spectral bands (O2 A- and CO2 bands). The red color corresponds to the O2 A-band and the blue color to the CO2 weak band. The different dashing of the lines indicates the different atmospheric scenarios.
Figure 8.
Dependence of the number of clusters and number of regression points with the mean error in percentage for the CO2 band for the ‘Aerosol 2’ scenario. The low-stream model used is the two-stream model.
Figure 8.
Dependence of the number of clusters and number of regression points with the mean error in percentage for the CO2 band for the ‘Aerosol 2’ scenario. The low-stream model used is the two-stream model.
Figure 9.
Comparison of the residuals for the methods PCA and CLSR for all the atmospheric scenarios (grey: ‘Clear sky’; blue: ‘Aerosol 1’; red: ‘Aerosol 2’; green: ‘Cloud 1’; yellow: ‘Cloud 2’) and gases (O2 A- and CO2 bands), when the low-stream model is (a) the two-stream model or (b) the single-scattering model. Note the differences in scales for the PCA technique for the O2 A-band with the rest of cases. The orange values on top of each box indicate the median values and the black values correspond to the IQR value.
Figure 9.
Comparison of the residuals for the methods PCA and CLSR for all the atmospheric scenarios (grey: ‘Clear sky’; blue: ‘Aerosol 1’; red: ‘Aerosol 2’; green: ‘Cloud 1’; yellow: ‘Cloud 2’) and gases (O2 A- and CO2 bands), when the low-stream model is (a) the two-stream model or (b) the single-scattering model. Note the differences in scales for the PCA technique for the O2 A-band with the rest of cases. The orange values on top of each box indicate the median values and the black values correspond to the IQR value.
Figure 10.
Convolved spectra for the multi-stream model and the two acceleration methods for the ‘Cloud 1’ scenario using PCA and CLSR methods for the sensors GOME-2, TROPOMI and GOSAT. For GOME-2 and TROPOMI the O2 A-band spectra are convolved, while for GOSAT the CO2 spectra are convolved.
Figure 10.
Convolved spectra for the multi-stream model and the two acceleration methods for the ‘Cloud 1’ scenario using PCA and CLSR methods for the sensors GOME-2, TROPOMI and GOSAT. For GOME-2 and TROPOMI the O2 A-band spectra are convolved, while for GOSAT the CO2 spectra are convolved.
Table 1.
Aerosol optical thickness used in the simulations for O2 A- and CO2 bands at the middle of the corresponding absorption band.
Table 1.
Aerosol optical thickness used in the simulations for O2 A- and CO2 bands at the middle of the corresponding absorption band.
| | O2 A-Band (760 nm) | CO2 Band (1610 nm) |
|---|
| Aerosol 1 | 0.2 | 0.08 |
| Aerosol 2 | 1.2 | 0.41 |
Table 2.
Mean relative error for the low-stream models (single-scattering and two-stream models) compared with the multi-stream model for the O2 A-band.
Table 2.
Mean relative error for the low-stream models (single-scattering and two-stream models) compared with the multi-stream model for the O2 A-band.
| Scenario | Single-Scattering Model | Two-Stream Model |
|---|
| (%) | (%) |
|---|
| Clear sky | 3.4 | 0.14 |
| Aerosol 1 | 36 | 1.0 |
| Aerosol 2 | 78 | 4.6 |
| Cloud 1 | 93 | 7.1 |
| Cloud 2 | 93 | 1.4 |
Table 3.
Mean relative error for the low-stream models (single-scattering and two-stream models) compared with the multi-stream model for the CO2 weak band.
Table 3.
Mean relative error for the low-stream models (single-scattering and two-stream models) compared with the multi-stream model for the CO2 weak band.
| Scenario | Single-Scattering Model | Two-Stream Model |
|---|
| (%) | (%) |
|---|
| Clear sky | 0.203 | 0.004 |
| Aerosol 1 | 14.7 | 0.40 |
| Aerosol 2 | 55.5 | 2.1 |
| Cloud 1 | 97.56 | 6.13 |
| Cloud 2 | 97.91 | 2.00 |
Table 4.
Computational time in seconds of the radiative transfer solution as a function of the number of streams, and speedup factors with respect to the case .
Table 4.
Computational time in seconds of the radiative transfer solution as a function of the number of streams, and speedup factors with respect to the case .
| Time (s) | Speedup Factor |
|---|
| 0 | 0.4 | 5800 |
| 1 | 3.2 | 725 |
| 2 | 12.4 | 187.1 |
| 4 | 34.4 | 67.4 |
| 8 | 110 | 21 |
| 16 | 550 | 4.2 |
| 32 | 2320 | - |
Table 5.
Speedup factor of the PCA-based () and CLSR methods with: the two-stream model () and single-scattering model ().
Table 5.
Speedup factor of the PCA-based () and CLSR methods with: the two-stream model () and single-scattering model ().
| | |
|---|
| 534 | 505 | 1294 |
Table 6.
Spectral ranges and FWHM of the Gaussian slit functions of the instruments used in the study: TROPOMI, GOME-2 and GOSAT.
Table 6.
Spectral ranges and FWHM of the Gaussian slit functions of the instruments used in the study: TROPOMI, GOME-2 and GOSAT.
| Instrument | Spectral Range | FWHM |
|---|
| TROPOMI | 710–775 nm | 0.183 nm |
| GOME-2 | 590–790 nm | 0.51 nm |
| GOSAT | 1.56–1.69 µm | 0.2 cm−1 |
Table 7.
Mean relative error for the convolved spectra compared with the multi-stream spectra for the PCA-based and CLSR methods and for the different atmospheric scenarios considered for the O2 A-band. In all cases, the low-stream model considered is the two-stream model. The instruments analyzed are GOME-2 and TROPOMI, which are compared with the non-convolved values.
Table 7.
Mean relative error for the convolved spectra compared with the multi-stream spectra for the PCA-based and CLSR methods and for the different atmospheric scenarios considered for the O2 A-band. In all cases, the low-stream model considered is the two-stream model. The instruments analyzed are GOME-2 and TROPOMI, which are compared with the non-convolved values.
| Scenario | O2 A-Band |
|---|
| GOME-2 | TROPOMI | Non-Convolved |
|---|
| | | | | |
|---|
| Clear sky | 0.021 | 0.004 | 0.021 | 0.004 | 0.022 | 0.006 |
| Aerosol 1 | 0.049 | 0.007 | 0.050 | 0.007 | 0.061 | 0.011 |
| Aerosol 2 | 0.837 | 0.019 | 0.837 | 0.019 | 0.856 | 0.026 |
| Cloud 1 | 1.23 | 0.011 | 1.23 | 0.011 | 1.24 | 0.017 |
| Cloud 2 | 2.92 | 0.006 | 2.92 | 0.006 | 2.93 | 0.009 |
Table 8.
Mean relative error for the convolved spectra compared with the multi-stream spectra for the PCA-based and CLSR methods and for the different atmospheric scenarios considered for the CO2 band. In all cases, the low-stream model considered is the two-stream model. The instrument analyzed is GOSAT, which is compared with the non-convolved values.
Table 8.
Mean relative error for the convolved spectra compared with the multi-stream spectra for the PCA-based and CLSR methods and for the different atmospheric scenarios considered for the CO2 band. In all cases, the low-stream model considered is the two-stream model. The instrument analyzed is GOSAT, which is compared with the non-convolved values.
| Scenario | CO2 Band |
|---|
| GOSAT | Non-Convolved |
|---|
| | | |
|---|
| Clear sky | 0.0003 | 0.0003 | 0.0006 | 0.0006 |
| Aerosol 1 | 0.0075 | 0.0067 | 0.010 | 0.012 |
| Aerosol 2 | 0.035 | 0.012 | 0.044 | 0.017 |
| Cloud 1 | 0.011 | 0.007 | 0.013 | 0.008 |
| Cloud 2 | 0.011 | 0.005 | 0.016 | 0.006 |