Radar Interferometry: 20 Years of Development in Time Series Techniques and Future Perspectives
Abstract
:1. Introduction
2. Background
3. Persistent Scattering Interferometry
The Related PSI Techniques and Advancements
4. Small Baseline
4.1. The SBAS Inversion
4.2. Overview Advancements
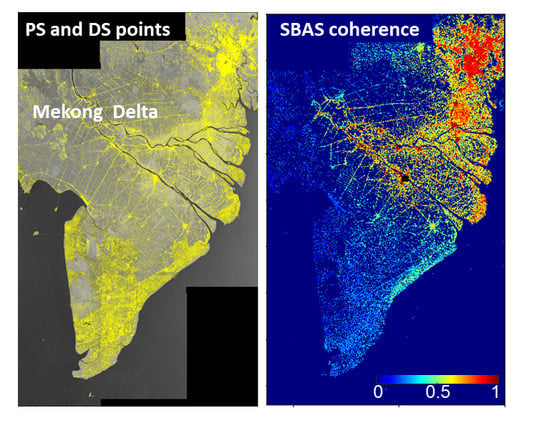
5. The Combination of PS and DS
5.1. The PSDS Technique
DS Selection
5.2. Overview Advancements
6. Looking forward in Big InSAR Data Era
- High Resolution Wide Swath (HRWS) systems [88,89], i.e., a typically 5 m resolution, are coupled with a 12 days revisit time and on a 250 km swath width. This would imply a 4 times improvement on Sentinel-1, and it could be a possibility for the Copernicus Next Generation systems. To achieve that new systems, i.e., Scan-on-Receive, should be used to exploit a taller antenna and hence improve its resolution.
- Satellite constellations (e.g., Capella (www.capellaspace.com), ICEYE (www.iceye.com), Umbra (www.umbralab.com), and XpressSAR (www.xpresssar.com)) are proposed. Indeed, mini-satellites are being used to achieve, in X-band, a meter scale resolution on a limited number of images per day. Then, the possible high number of satellites and their agility would lead to enticing extremely short times to achieve a high-resolution image and always shorter than one day revisit.
- Many satellite systems have been identified and assessed [89,90]. These satellite formations consist of many mini-satellites combined in a multiple-transmit multiple-receive (MIMO) or a single-transmit multiple-receive (SIMO) structure. They can achieve results similar to the principle of HRWS, but maybe with more robust and flexible systems. It should be observed, though, that the formations are difficult to localize their obits precisely, and therefore it would not be possible to guarantee their performances, unless on a statistical basis. Furthermore, many baselines would be available at the same time due to the presence of many satellites, e.g., 4 or 5, and hence up to 10 different baselines. This would allow doing tomography without effects of temporal decorrelation [91] and thus could be used for foliage penetration and forest studies [92,93].
- GEO-synchronous systems are proposed in various modes [94]. The first case is an L-band system [95], i.e., a wide antenna (about 25 m diameter), proposed by Chinese scientists and it is soon be launched. The second case is a smaller C-band system (about 7.5 m antenna diameter). This is being studied within the framework of the ESA Earth Explorer 10-th round, i.e., G-Class [96], and might be the system selected in future decisions to be taken in 2020/2021. The smaller antenna of the European proposal implies a longer observation time in order to achieve good noise performances. However, both systems allow daily observations (and in the European case, hourly) on the part of the globe fronting the satellite. In other words, the fast availability of new images, in the cases of need, will be obtained. The objective is to study the soil moisture and the temporal evolution of columnar water vapor (on a km scale and in time of minutes), that was said to be a disturbance for InSAR processing, but it is going now to be the signal to be studied.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hanssen, R.F. Radar Interferometry: Data Interpretation and Error Analysis; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2001. [Google Scholar]
- Zebker, H.A.; Villasenor, J. Decorrelation in interferometric radar echoes. IEEE Trans. Geosci. Remote Sens. 1992, 30, 950–959. [Google Scholar] [CrossRef] [Green Version]
- Zebker, H.A.; Rosen, P.A.; Hensley, S. Atmospheric effects in interferometric synthetic aperture radar surface deformation and topographic maps. J. Geophys. Res. Solid Earth. 1997, 102, 7547–7563. [Google Scholar] [CrossRef]
- Ferreti, A.; Prati, C.; Rocca, F. Nonlinear subsidence rate estimation using permanent scatterers in differential SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2000, 38, 2202–2212. [Google Scholar] [CrossRef] [Green Version]
- Ferretti, A.; Prati, C.; Rocca, F. Permanent scatterers in SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2001, 39, 8–20. [Google Scholar] [CrossRef]
- Hooper, A.; Zebker, H.; Segall, P.; Kampes, B. A new method for measuring deformation on volcanoes and other natural terrains using InSAR persistent scatterers. Geophys. Res. Lett. 2004, 31, L23661. [Google Scholar] [CrossRef]
- Berardino, P.; Fornaro, G.; Lanari, R.; Sansosti, E. A New Algorithm for Surface Deformation Monitoring Based on Small Baseline Differential SAR Interferograms. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2375–2383. [Google Scholar] [CrossRef] [Green Version]
- Lanari, R.; Mora, O.; Manunta, M.; Mallorqui, J.J.; Berardino, P.; Sansosti, E. A small-baseline approach for investigating deformations on full-resolution differential SAR interferograms. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1377–1386. [Google Scholar] [CrossRef]
- Hooper, A. A multi-temporal InSAR method incorporating both persistent scatterer and small baseline approaches. Geophys. Res. Lett. 2008, 35, 1–5. [Google Scholar] [CrossRef] [Green Version]
- Ferretti, A.; Fumagalli, A.; Novali, F.; Prati, C.; Rocca, F.; Rucci, A. A New Algorithm for Processing Interferometric Data-Stacks: SqueeSAR. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3460–3470. [Google Scholar] [CrossRef]
- Torres, R.; Snoeij, P.; Geudtner, D.; Bibby, D.; Davidson, M.; Attema, E.; Rommena, B.; Flourya, N.; Brown, M.; Travera, I.G.; et al. GMES Sentinel-1 mission. Remote Sens. Environ. 2012, 120, 9–24. [Google Scholar] [CrossRef]
- De Zan, F.; Monti Guarnieri, A. TOPSAR: Terrain Observation by Progressive Scans. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2352–2360. [Google Scholar] [CrossRef]
- Hajnsek, I.; Shimada, M.; Eineder, M.; Papathanassiou, K.; Motohka, T.; Watanabe, M.; Ohki, M.; De Zan, F.; Lopez-Dekker, P.; Krieger, G.; et al. Tandem-L: Science Requirements and Mission Concept. In Proceedings of the EUSAR 2014; 10th European Conference on Synthetic Aperture Radar, Berlin, Germany, 3–5 June 2014; pp. 1–4. [Google Scholar]
- Rosen, P.A.; Kim, Y.; Kumar, R.; Misra, T.; Bhan, R.; Sagi, V.R. Global persistent SAR sampling with the NASA-ISRO SAR (NISAR) mission. In Proceedings of the 2017 IEEE Radar Conference (RadarConf), Seattle, WA, USA, 8–12 May 2017; pp. 0410–0414. [Google Scholar]
- Ghiglia, D.C.; Pritt, M.D. Two-Dimensional Phase Unwrapping: Theory, Algorithms, and Software; John Wiley & Sons, Inc.: New York, NY, USA, 1998. [Google Scholar]
- Werner, C.; Wegmuller, U.; Strozzi, T.; Wiesmann, A. Interferometric point target analysis for deformation mapping. In Proceedings of the 2003 IEEE International Geoscience and Remote Sensing Symposium, Toulouse, France, 21–25 July 2003; Volume 7, pp. 4362–4364. [Google Scholar] [CrossRef]
- Kampes, B. Radar Interferometry: Persistent Scatterer Technique; Springer Publishing Company: Dordrecht, The Netherlands, 2006. [Google Scholar]
- Perissin, D.; Wang, T. Repeat-Pass SAR Interferometry With Partially Coherent Targets. IEEE Trans. Geosci. Remote Sens. 2012, 50, 271–280. [Google Scholar] [CrossRef]
- Devanthéry, N.; Crosetto, M.; Monserrat, O.; Cuevas-González, M.; Crippa, B. An Approach to Persistent Scatterer Interferometry. Remote Sens. 2014, 6, 6662–6679. [Google Scholar] [CrossRef] [Green Version]
- Siddique, M.A.; Wegmüller, U.; Hajnsek, I.; Frey, O. Single-Look SAR Tomography as an Add-On to PSI for Improved Deformation Analysis in Urban Areas. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6119–6137. [Google Scholar] [CrossRef]
- Mora, O.; Mallorqui, J.J.; Broquetas, A. Linear and nonlinear terrain deformation maps from a reduced set of interferometric SAR images. IEEE Trans. Geosci. Remote Sens. 2003, 41, 2243–2253. [Google Scholar] [CrossRef]
- Schmidt, D.A.; Bürgmann, R. Time-dependent land uplift and subsidence in the Santa Clara valley, California, from a large interferometric synthetic aperture radar data set. J. Geophys. Res. Solid Earth 2003, 108. [Google Scholar] [CrossRef] [Green Version]
- Crosetto, M.; Crippa, B.; Biescas, E. Early detection and in-depth analysis of deformation phenomena by radar interferometry. Eng. Geol. 2005, 79, 81–91. [Google Scholar] [CrossRef]
- López-Quiroz, P.; Doin, M.P.; Tupin, F.; Briole, P.; Nicolas, J.M. Time series analysis of Mexico City subsidence constrained by radar interferometry. J. Appl. Geophys. 2009, 69, 1–15. [Google Scholar] [CrossRef]
- Hetland, E.A.; Musé, P.; Simons, M.; Lin, Y.N.; Agram, P.S.; DiCaprio, C.J. Multiscale InSAR Time Series (MInTS) analysis of surface deformation. J. Geophys. Res. Solid Earth 2012, 117. [Google Scholar] [CrossRef] [Green Version]
- Casu, F.; Elefante, S.; Imperatore, P.; Zinno, I.; Manunta, M.; De Luca, C.; Lanari, R. SBAS-DInSAR Parallel Processing for Deformation Time-Series Computation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 3285–3296. [Google Scholar] [CrossRef]
- Manunta, M.; De Luca, C.; Zinno, I.; Casu, F.; Manzo, M.; Bonano, M.; Fusco, A.; Pepe, A.; Onorato, G.; Berardino, P.; et al. The Parallel SBAS Approach for Sentinel-1 Interferometric Wide Swath Deformation Time-Series Generation: Algorithm Description and Products Quality Assessment. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6259–6281. [Google Scholar] [CrossRef]
- Goel, K.; Adam, N. A Distributed Scatterer Interferometry Approach for Precision Monitoring of Known Surface Deformation Phenomena. IEEE Trans. Geosci. Remote Sens. 2014, 52, 5454–5468. [Google Scholar] [CrossRef]
- Samiei-Esfahany, S.; Martins, J.E.; van Leijen, F.; Hanssen, R.F. Phase Estimation for Distributed Scatterers in InSAR Stacks Using Integer Least Squares Estimation. IEEE Trans. Geosci. Remote Sens. 2016, 54, 5671–5687. [Google Scholar] [CrossRef] [Green Version]
- Cao, N.; Lee, H.; Jung, H.C. A Phase-Decomposition-Based PSInSAR Processing Method. IEEE Trans. Geosci. Remote Sens. 2016, 54, 1074–1090. [Google Scholar] [CrossRef]
- Engelbrecht, J.; Inggs, M.R. Coherence Optimization and Its Limitations for Deformation Monitoring in Dynamic Agricultural Environments. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 5647–5654. [Google Scholar] [CrossRef]
- Ansari, H.; De Zan, F.; Bamler, R. Sequential Estimator: Toward Efficient InSAR Time Series Analysis. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5637–5652. [Google Scholar] [CrossRef] [Green Version]
- Mullissa, A.G.; Perissin, D.; Tolpekin, V.A.; Stein, A. Polarimetry-Based Distributed Scatterer Processing Method for PSI Applications. IEEE Trans. Geosci. Remote Sens. 2018, 56, 3371–3382. [Google Scholar] [CrossRef]
- Der Kooij, V. Coherent Target Analysis; Fringe Workshop: Frascati, Italy, 2003. [Google Scholar]
- Costantini, M.; Falco, S.; Malvarosa, F.; Minati, F. A New Method for Identification and Analysis of Persistent Scatterers in Series of SAR Images. In Proceedings of the 2008 IEEE International Geoscience and Remote Sensing Symposium, Boston, MA, USA, 7–11 July 2008; Volume 2, pp. 449–452. [Google Scholar] [CrossRef]
- Shanker, P.; Zebker, H. Persistent scatterer selection using maximum likelihood estimation. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
- Colesanti, C.; Ferretti, A.; Novali, F.; Prati, C.; Rocca, F. SAR monitoring of progressive and seasonal ground deformation using the permanent scatterers technique. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1685–1701. [Google Scholar] [CrossRef] [Green Version]
- Monserrat, O.; Crosetto, M.; Cuevas, M.; Crippa, B. The Thermal Expansion Component of Persistent Scatterer Interferometry Observations. IEEE Geosci. Remote Sens. Lett. 2011, 8, 864–868. [Google Scholar] [CrossRef]
- Hooper, A.; Zebker, H.A. Phase unwrapping in three dimensions with application to InSAR time series. JOSA A 2007, 24, 2737–2747. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gini, F.; Lombardini, F.; Montanari, M. Layover solution in multibaseline SAR interferometry. IEEE Trans. Aerosp. Electron. Syst. 2002, 38, 1344–1356. [Google Scholar] [CrossRef]
- Jia, H.; Liu, L. A technical review on persistent scatterer interferometry. J. Mod. Transp. 2016, 24, 153–158. [Google Scholar] [CrossRef] [Green Version]
- Hooper, A.; Ofeigsson, B.; Sigmundsson, F. Increased capture of magma in the crust promoted by ice-cap retreat in Iceland. Nat. Geosci. 2011, 4, 783–786. [Google Scholar] [CrossRef]
- Ferrero, A.; Novali, F.; Prati, C.; Rocca, F. Advances in Permanent Scatterers analysis. Semi and temporary PS. In Proceedings of the European Conference on Synthetic Aperture Radar EUSAR 2004, Ulm, Germany, 25–27 May 2004. [Google Scholar]
- Fialko, Y. Interseismic strain accumulation and the earthquake potential on the southern San Andreas fault system. Nature 2006, 441, 968–971. [Google Scholar] [CrossRef] [PubMed]
- Pepe, A.; Lanari, R. On the Extension of the Minimum Cost Flow Algorithm for Phase Unwrapping of Multitemporal Differential SAR Interferograms. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2374–2383. [Google Scholar] [CrossRef]
- Yunjun, Z.; Fattahi, H.; Amelung, F. Small baseline InSAR time series analysis: Unwrapping error correction and noise reduction. Comput. Geosci. 2019, 133, 104331. [Google Scholar] [CrossRef] [Green Version]
- Doin, M.P.; Lodge, F.; Guillaso, S.; Jolivet, R.; Lasserre, C.; Ducret, G.; Grandin, R.; Pathier, E.; Pinel, V. Presentation of the Small Baseline NSBAS Processing Chain on a Case Example: The Etna Deformation Monitoring from 2003 to 2010 Using Envisat Data; Fringe Workshop: Frascati, Italy, 2011. [Google Scholar]
- Hong, S.; Wdowinski, S.; Kim, S.; Won, J. Multi-temporal monitoring of wetland water levels in the Florida Everglades using interferometric synthetic aperture radar (InSAR). Remote Sens. Environ. 2010, 114, 2436–2447. [Google Scholar] [CrossRef]
- Agram, P.S.; Jolivet, R.; Riel, B.; Lin, Y.N.; Simons, M.; Hetland, E.; Doin, M.P.; Lasserre, C. New Radar Interferometric Time Series Analysis Toolbox Released. Eos Trans. Am. Geophys. Union 2013, 94, 69–70. [Google Scholar] [CrossRef] [Green Version]
- Fattahi, H.; Amelung, F. InSAR bias and uncertainty due to the systematic and stochastic tropospheric delay. J. Geophys. Res. Solid Earth 2015, 120, 8758–8773. [Google Scholar] [CrossRef] [Green Version]
- Doin, M.P.; Lasserre, C.; Peltzer, G.; Cavalié, O.; Doubre, C. Corrections of stratified tropospheric delays in SAR interferometry: Validation with global atmospheric models. J. Appl. Geophys. 2009, 69, 35–50. [Google Scholar] [CrossRef]
- Bekaert, D.P.S.; Hooper, A.; Wright, T.J. A spatially variable power law tropospheric correction technique for InSAR data. J. Geophys. Res. Solid Earth 2015, 120, 1345–1356. [Google Scholar] [CrossRef]
- Jolivet, R.; Grandin, R.; Lasserre, C.; Doin, M.P.; Peltzer, G. Systematic InSAR tropospheric phase delay corrections from global meteorological reanalysis data. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef] [Green Version]
- Jolivet, R.; Agram, P.S.; Lin, N.Y.; Simons, M.; Doin, M.P.; Peltzer, G.; Li, Z. Improving InSAR geodesy using Global Atmospheric Models. J. Geophys. Res. Solid Earth 2014, 119, 2324–2341. [Google Scholar] [CrossRef]
- Yu, C.; Li, Z.; Penna, N.T. Interferometric synthetic aperture radar atmospheric correction using a GPS-based iterative tropospheric decomposition model. Remote Sens. Environ. 2018, 204, 109–121. [Google Scholar] [CrossRef]
- Li, Z.; Fielding, E.J.; Cross, P.; Preusker, R. Advanced InSAR atmospheric correction: MERIS/MODIS combination and stacked water vapour models. Int. J. Remote Sens. 2009, 30, 3343–3363. [Google Scholar] [CrossRef]
- Onn, F.; Zebker, H.A. Correction for interferometric synthetic aperture radar atmospheric phase artifacts using time series of zenith wet delay observations from a GPS network. J. Geophys. Res. Solid Earth 2006, 111. [Google Scholar] [CrossRef]
- Yu, C.; Li, Z.; Penna, N.T.; Crippa, P. Generic Atmospheric Correction Model for Interferometric Synthetic Aperture Radar Observations. J. Geophys. Res. Solid Earth 2018, 123, 9202–9222. [Google Scholar] [CrossRef]
- Chen, C.W.; Zebker, H.A. Phase unwrapping for large SAR interferograms: Statistical segmentation and generalized network models. IEEE Trans. Geosci. Remote Sens. 2002, 40, 1709–1719. [Google Scholar] [CrossRef] [Green Version]
- Biggs, J.; Wright, T.; Lu, Z.; Parsons, B. Multi-interferogram method for measuring interseismic deformation: Denali Fault, Alaska. Geophys. J. Int. 2007, 170, 1165–1179. [Google Scholar] [CrossRef] [Green Version]
- De Zan, F.; Parizzi, A.; Prats-Iraola, P.; López-Dekker, P. A SAR Interferometric Model for Soil Moisture. IEEE Trans. Geosci. Remote Sens. 2014, 52, 418–425. [Google Scholar] [CrossRef] [Green Version]
- Hussain, E.; Hooper, A.; Wright, T.J.; Walters, R.J.; Bekaert, D.P.S. Interseismic strain accumulation across the central North Anatolian Fault from iteratively unwrapped InSAR measurements. J. Geophys. Res. Solid Earth 2016, 121, 9000–9019. [Google Scholar] [CrossRef] [Green Version]
- Pepe, A.; Bertran Ortiz, A.; Lundgren, P.R.; Rosen, P.A.; Lanari, R. The Stripmap–ScanSAR SBAS Approach to Fill Gaps in Stripmap Deformation Time Series With ScanSAR Data. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4788–4804. [Google Scholar] [CrossRef]
- Fornaro, G.; Monti Guarnieri, A.; Pauciullo, A.; De-Zan, F. Maximum liklehood multi-baseline SAR interferometry. IEE Proc. Radar Sonar Navig. 2006, 153, 279–288. [Google Scholar] [CrossRef] [Green Version]
- Ferretti, A.; Novali, F.; Zan, F.D.; Prati, C.; Rocca, F. Moving from PS to slowly decorrelating targets: A prospective view. In Proceedings of the European Conference on Synthetic Aperture Radar EUSAR 2008, Friedrichshafen, Germany, 2–5 June 2008. [Google Scholar]
- Rocca, F. Modeling Interferogram Stacks. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3289–3299. [Google Scholar] [CrossRef]
- Guarnieri, A.M.; Tebaldini, S. On the Exploitation of Target Statistics for SAR Interferometry Applications. IEEE Trans. Geosci. Remote Sens. 2008, 46, 3436–3443. [Google Scholar] [CrossRef]
- Ho Tong Minh, D.; Tran, Q.C.; Pham, Q.N.; Dang, T.T.; Nguyen, D.A.; El-Moussawi, I.; Le Toan, T. Measuring Ground Subsidence in Ha Noi Through the Radar Interferometry Technique Using TerraSAR-X and Cosmos SkyMed Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 3874–3884. [Google Scholar] [CrossRef]
- Battiti, R.; Masulli, F. BFGS Optimization for Faster and Automated Supervised Learning. In Proceedings of the International Neural Network Conference, Palais Des Congres, Paris, France, 9–13 July 1990; Springer: Dordrecht, The Netherlands, 1990; pp. 757–760. [Google Scholar] [CrossRef]
- Ho Tong Minh, D.; Ngo, Y.N. Tomosar platform supports for Sentinel-1 tops persistent scatterers interferometry. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 1680–1683. [Google Scholar] [CrossRef]
- Ho Tong Minh, D.; Van Trung, L.; Toan, T.L. Mapping Ground Subsidence Phenomena in Ho Chi Minh City through the Radar Interferometry Technique Using ALOS PALSAR Data. Remote Sens. 2015, 7, 8543–8562. [Google Scholar] [CrossRef] [Green Version]
- Cohen-Waeber, J.; Bürgmann, R.; Chaussard, E.; Giannico, C.; Ferretti, A. Spatiotemporal Patterns of Precipitation-Modulated Landslide Deformation From Independent Component Analysis of InSAR Time Series. Geophys. Res. Lett. 2018, 45, 1878–1887. [Google Scholar] [CrossRef]
- Lv, X.; Yazıcı, B.; Zeghal, M.; Bennett, V.; Abdoun, T. Joint-Scatterer Processing for Time-Series InSAR. IEEE Trans. Geosci. Remote Sens. 2014, 52, 7205–7221. [Google Scholar]
- Shamshiri, R.; Nahavandchi, H.; Motagh, M.; Hooper, A. Efficient Ground Surface Displacement Monitoring Using Sentinel-1 Data: Integrating Distributed Scatterers (DS) Identified Using Two-Sample t-Test with Persistent Scatterers (PS). Remote Sens. 2018, 10, 794. [Google Scholar] [CrossRef] [Green Version]
- Jiang, M.; Ding, X.; Hanssen, R.F.; Malhotra, R.; Chang, L. Fast Statistically Homogeneous Pixel Selection for Covariance Matrix Estimation for Multitemporal InSAR. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1213–1224. [Google Scholar] [CrossRef]
- Spaans, K.; Hooper, A. InSAR processing for volcano monitoring and other near-real time applications. J. Geophys. Res. Solid Earth 2016, 121, 2947–2960. [Google Scholar] [CrossRef] [Green Version]
- Narayan, A.B.; Tiwari, A.; Dwivedi, R.; Dikshit, O. A Novel Measure for Categorization and Optimal Phase History Retrieval of Distributed Scatterers for InSAR Applications. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5843–5849. [Google Scholar] [CrossRef]
- Cao, N.; Lee, H.; Jung, H.C. Mathematical Framework for Phase-Triangulation Algorithms in Distributed-Scatterer Interferometry. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1838–1842. [Google Scholar] [CrossRef]
- Fornaro, G.; Verde, S.; Reale, D.; Pauciullo, A. CAESAR: An Approach Based on Covariance Matrix Decomposition to Improve Multibaseline–Multitemporal Interferometric SAR Processing. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2050–2065. [Google Scholar] [CrossRef]
- Ansari, H.; De Zan, F.; Bamler, R. Efficient Phase Estimation for Interferogram Stacks. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4109–4125. [Google Scholar] [CrossRef]
- Xu, X.; Sandwell, D.T. Toward Absolute Phase Change Recovery With InSAR: Correcting for Earth Tides and Phase Unwrapping Ambiguities. IEEE Trans. Geosci. Remote Sens. 2020, 58, 726–733. [Google Scholar] [CrossRef]
- Ansari, H.; Zan, F.D.; Parizzi, A. Study of Systematic Bias in Measuring Surface Deformation with SAR Interferometry. IEEE Trans. Geosci. Remote Sens. 2020, 58, 1–12. [Google Scholar]
- De Zan, F.; Zonno, M.; López-Dekker, P. Phase Inconsistencies and Multiple Scattering in SAR Interferometry. IEEE Trans. Geosci. Remote Sens. 2015, 53, 6608–6616. [Google Scholar] [CrossRef] [Green Version]
- Zwieback, S.; Liu, X.; Antonova, S.; Heim, B.; Bartsch, A.; Boike, J.; Hajnsek, I. A Statistical Test of Phase Closure to Detect Influences on DInSAR Deformation Estimates Besides Displacements and Decorrelation Noise: Two Case Studies in High-Latitude Regions. IEEE Trans. Geosci. Remote Sens. 2016, 54, 5588–5601. [Google Scholar] [CrossRef]
- Monti-Guarnieri, A.V.; Brovelli, M.A.; Manzoni, M.; Mariotti d’Alessandro, M.; Molinari, M.E.; Oxoli, D. Coherent Change Detection for Multipass SAR. IEEE Trans. Geosci. Remote Sens. 2018, 56, 6811–6822. [Google Scholar] [CrossRef]
- Crosetto, M.; Monserrat, O.; Cuevas-González, M.; Devanthéry, N.; Crippa, B. Persistent Scatterer Interferometry: A review. ISPRS J. Photogramm. Remote Sens. 2016, 115, 78–89. [Google Scholar] [CrossRef] [Green Version]
- Zebker, H.A. User-Friendly InSAR Data Products: Fast and Simple Timeseries Processing. IEEE Geosci. Remote Sens. Lett. 2017, 14, 2122–2126. [Google Scholar] [CrossRef]
- Krieger, G.; de Almeida, F.Q.; Huber, S.; Villano, M.; Younis, M.; Moreira, A.; del Castillo, J.; Rodriguez-Cassola, M.; Prats, P.; Petrolati, D.; et al. Advanced L-Band SAR System Concepts for High-Resolution Ultra-Wide-Swath SAR Imaging; ESA Advanced RF Sensors and Remote Sensing Instruments (ARSI): Noordwijk, The Netherlands, 2017. [Google Scholar]
- Mittermayer, J.; Krieger, G.; Bojarski, A.; Zonno, M.; Moreira, A. A MirrorSAR Case Study Based on the X-Band High Resolution Wide Swath Satellite (HRWS). In Proceedings of the European Conference on Synthetic Aperture Radar, Leipzig, Germany, 15–18 June 2020. [Google Scholar]
- Guccione, P.; Monti Guarnieri, A.; Rocca, F.; Giudici, D.; Gebert, N. Along-Track Multistatic Synthetic Aperture Radar Formations of Minisatellites. Remote Sens. 2020, 12, 124. [Google Scholar] [CrossRef] [Green Version]
- Ho Tong Minh, D.; Tebaldini, S.; Rocca, F.; Le Toan, T.; Borderies, P.; Koleck, T.; Albinet, C.; Hamadi, A.; Villard, L. Vertical Structure of P-Band Temporal Decorrelation at the Paracou Forest: Results From TropiScat. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1438–1442. [Google Scholar] [CrossRef] [Green Version]
- Ho Tong Minh, D.; Le Toan, T.; Rocca, F.; Tebaldini, S.; Mariotti d’Alessandro, M.; Villard, L. Relating P-band Synthetic Aperture Radar Tomography to Tropical Forest Biomass. IEEE Trans. Geosci. Remote Sens. 2014, 52, 967–979. [Google Scholar] [CrossRef]
- Ho Tong Minh, D.; Tebaldini, S.; Rocca, F.; Le Toan, T.; Villard, L.; Dubois-Fernandez, P. Capabilities of BIOMASS Tomography for Investigating Tropical Forests. IEEE Trans. Geosci. Remote Sens. 2015, 53, 965–975. [Google Scholar] [CrossRef]
- Guarnieri, A.M.; Rocca, F. Options for continuous radar Earth observations. Sci. China Inf. Sci. 2017, 60, 060301. [Google Scholar] [CrossRef]
- Hu, C.; Li, Y.; Dong, X.; Wang, R.; Ao, D. Performance Analysis of L-Band Geosynchronous SAR Imaging in the Presence of Ionospheric Scintillation. IEEE Trans. Geosci. Remote Sens. 2017, 55, 159–172. [Google Scholar] [CrossRef]
- Hobbs, S.E.; Monti-Guarnieri, A. Geosynchronous Continental Land-Atmosphere Sensing System (G-Class): Persistent Radar Imaging for Earth Science. In Proceedings of the 2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 8621–8624. [Google Scholar] [CrossRef] [Green Version]



| Method Reference | Interferogram Network | Pixel Selection Criteria | Deformation Model and Others |
|---|---|---|---|
| Persistent Scattering Interferometry | |||
| Ferretti et al. (2000, 2001) [4,5] | Single master | Amplitude dispersion | Linear deformation |
| Werner et al. (2003) [16] | Single master | Amplitude dispersion and spectral phase diversity | Linear deformation |
| Hooper et al. (2004) [6] | Single master | Phase stability | Spatial smoothness and 3D phase unwrapping |
| Kampes (2006) [17] | Single master | Amplitude dispersion | Different types of deformation models |
| Perissin and Wang (2012) [18] | Target-dependent subset | Quasi-PS approach | Linear deformation |
| Devanthéry et al. (2014) [19] | Small baseline | Amplitude dispersion and Cousin PS | Spatial smoothness |
| Siddique et al. (2016) [20] | Single master | Amplitude dispersion and spectral diversity | Different types of deformation models and tomography |
| Small baseline | |||
| Berardino et al. (2002) [7] | Small baseline | Coherence | Spatial smoothness |
| Mora et al. (2003) [21] | Small baseline | Coherence | Linear deformation |
| Schmidt and Bürgmann (2003) [22] | Small baseline | Coherence | Spatial and temporal smoothness |
| Lanari et al. (2004) [8] | Small baseline | Coherence | Spatial smoothness and full-resolution |
| Crosetto et al. (2005) [23] | Small baseline | Coherence | Stepwise linear function |
| López-Quiroz et al. (2009) [24] | Small baseline | Coherence | Spatial smoothness |
| Hetland et al. (2012) [25] | Small baseline | Coherence | Different types of deformation models |
| Casu et al. (2014) [26] and Manuta et al. (2019) [27] | Small baseline | Coherence | Spatial smoothness and parallel |
| The combination of PS and DS | |||
| Hooper et al. (2008) [9] | Single master and small baseline | Phase stability | Spatial smoothness and 3D phase unwrapping |
| Ferretti et al. (2011) [10] | Full stacking | Statistical homogeneity test | Linear deformation and phase linking |
| Goel and Adam (2014) [28] | Small baseline | Statistical homogeneity test | Linear deformation |
| Samiei-Esfahany et al. (2016) [29] | Full stacking | Statistical homogeneity test | Different types of deformation and phase linking |
| Cao et al. (2016) [30], Engelbrecht and Inggs (2016) [31] | Full stacking | Statistical homogeneity test | Linear deformation, phase linking, and multiple scattering |
| Ansari et al. (2017) [32] | Efficient stacking | Statistical homogeneity test | Linear deformation and phase linking |
| Mullissa et al. (2018) [33] | Full stacking | Statistical homogeneity test | Linear deformation, phase linking, and polarization |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
HO TONG MINH, D.; Hanssen, R.; Rocca, F. Radar Interferometry: 20 Years of Development in Time Series Techniques and Future Perspectives. Remote Sens. 2020, 12, 1364. https://doi.org/10.3390/rs12091364
HO TONG MINH D, Hanssen R, Rocca F. Radar Interferometry: 20 Years of Development in Time Series Techniques and Future Perspectives. Remote Sensing. 2020; 12(9):1364. https://doi.org/10.3390/rs12091364
Chicago/Turabian StyleHO TONG MINH, Dinh, Ramon Hanssen, and Fabio Rocca. 2020. "Radar Interferometry: 20 Years of Development in Time Series Techniques and Future Perspectives" Remote Sensing 12, no. 9: 1364. https://doi.org/10.3390/rs12091364
APA StyleHO TONG MINH, D., Hanssen, R., & Rocca, F. (2020). Radar Interferometry: 20 Years of Development in Time Series Techniques and Future Perspectives. Remote Sensing, 12(9), 1364. https://doi.org/10.3390/rs12091364