Above-Ground Biomass Retrieval over Tropical Forests: A Novel GNSS-R Approach with CyGNSS
Abstract
:1. Introduction
- What is the DDMs’ response to the interaction of GNSS signals with tropical forests?
- What is the GNSS signals saturation level (if any) over tropical forests?
- What is the optimum GNSS satellites elevation angle for biomass estimation over tropical forests?
2. Exploiting CyGNSS for Biomass Monitoring
2.1. Background
2.2. Motivation
3. Methodology
3.1. Definition of the Selected CyGNSS Observables
3.2. Auxiliary Forests Vegetation Parameters
3.3. Strategy
4. Performance Analysis
4.1. Introduction
4.2. Sensitivity Analysis as a Function of the Elevation Angle
4.3. Evaluation with SMAP-derived VOD, PI, and SMC
4.4. First Evidences of Biomass Retrieval Using an Empirical Approach
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A: Study Sites


Appendix B: Reference Data
Appendix B.1. GLAS ICESat-1 Canopy Height Map
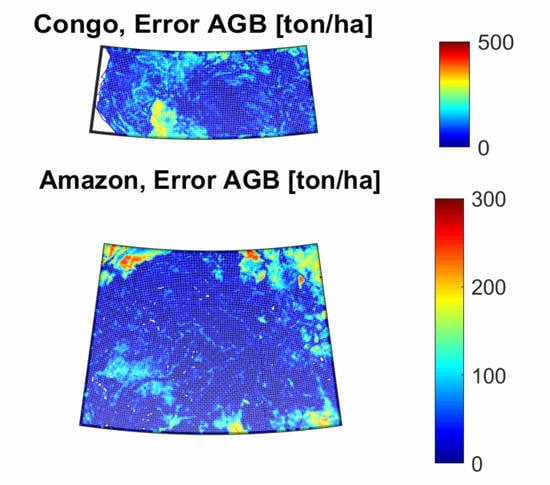
Appendix B.2. Pantropical Above-Ground Biomass Map
Appendix C: Sensitivity Analysis
| AGB [ton/ha] | 50 | 100 | 150 | 200 | 250 | 300 | 350 |
|---|---|---|---|---|---|---|---|
| [20, 30]° | 1.53 | 1.21 | 0.90 | 0.55 | 0.35 | 0.33 | 0.30 |
| [40, 50]° | - | 1.05 | 0.93 | 0.77 | 0.58 | 0.37 | 0.17 |
| [60, 70]° | - | 1 | 0.87 | 0.71 | 0.53 | 0.35 | 0.19 |
| [80, 90]° | - | - | - | 0.62 | 0.45 | 0.22 | - |
| AGB [ton/ha] | 50 | 100 | 150 | 200 | 250 | 300 | 350 |
|---|---|---|---|---|---|---|---|
| [20, 30]° | - | 1.07 | 0.75 | 0.40 | 0.10 | - | - |
| [40, 50]° | - | 1.15 | 0.85 | 0.53 | 0.18 | - | - |
| [60, 70]° | - | - | 0.70 | 0.60 | 0.20 | - | - |
| [80, 90]° | - | - | 0.70 | 0.42 | 0.12 | - | - |
| AGB [ton/ha] | 50 | 100 | 150 | 200 | 250 | 300 | 350 |
|---|---|---|---|---|---|---|---|
| [20, 30]° | - | - | - | - | 17.1 | 15.5 | - |
| [40, 50]° | - | - | - | 19.3 | 25.2 | 27.4 | 23.1 |
| [60, 70]° | - | - | 10.5 | 21.2 | 26 | 26.1 | 17.5 |
| [80, 90]° | - | - | - | - | 16.2 | 21.3 | 16.2 |
| AGB [ton/ha] | 50 | 100 | 150 | 200 | 250 | 300 | 350 |
|---|---|---|---|---|---|---|---|
| [20, 30]° | - | - | 15.8 | 16 | 9.5 | - | - |
| [40, 50]° | - | 17.2 | 18 | 16 | 11.5 | 9 | - |
| [60, 70]° | - | 16 | 17.8 | 16 | 10.4 | - | - |
| [80, 90]° | - | - | 15.8 | 14 | 9.5 | - | - |
| AGB [ton/ha] | 50 | 100 | 150 | 200 | 250 | 300 | 350 |
|---|---|---|---|---|---|---|---|
| [20, 30]° | 1.53 | 1.21 | 0.90 | 0.55 | 0.35 | 0.33 | 0.30 |
| [40, 50]° | - | 1.05 | 0.93 | 0.77 | 0.58 | 0.37 | 0.17 |
| [60, 70]° | - | 1 | 0.87 | 0.71 | 0.53 | 0.35 | 0.19 |
| [80, 90]° | - | - | - | 0.62 | 0.45 | 0.22 | - |
| AGB [ton/ha] | 50 | 100 | 150 | 200 | 250 | 300 | 350 |
|---|---|---|---|---|---|---|---|
| [20, 30]° | - | 1.07 | 0.75 | 0.40 | 0.10 | - | - |
| [40, 50]° | - | 1.15 | 0.85 | 0.53 | 0.18 | - | - |
| [60, 70]° | - | - | 0.70 | 0.60 | 0.20 | - | - |
| [80, 90]° | - | - | 0.70 | 0.42 | 0.12 | - | - |
| AGB [ton/ha] | 50 | 100 | 150 | 200 | 250 | 300 | 350 |
|---|---|---|---|---|---|---|---|
| [20, 30]° | - | - | - | - | 1.71 | 1.55 | - |
| [40, 50]° | - | - | - | 1.93 | 2.52 | 2.74 | 2.31 |
| [60, 70]° | - | - | 1.05 | 2.12 | 2.6 | 2.61 | 1.75 |
| [80, 90]° | - | - | - | - | 1.62 | 2.13 | 1.62 |
| AGB [ton/ha] | 50 | 100 | 150 | 200 | 250 | 300 | 350 |
|---|---|---|---|---|---|---|---|
| [20, 30]° | - | - | 1.58 | 1.6 | 0.95 | - | - |
| [40, 50]° | - | 1.72 | 1.8 | 1.6 | 1.15 | 0.9 | - |
| [60, 70]° | - | 1.6 | 1.78 | 1.6 | 1.04 | - | - |
| [80, 90]° | - | - | 1.58 | 1.4 | 0.95 | - | - |
References
- Barker, C.; Barry, R.; Brady, M.; Brown, J.; Christiansen, H.; Cihlar, J.; Clow, G.; Csiszar, I.; Dolman, H.; Famiglietti, J.; et al. Terrestrial Essential Climate Variables for Climate Assessment Mitigation and Adaptation; Food and Agriculture Organization (FAO) of the United Nations: Rome, Italy, 2008. [Google Scholar]
- Houghton, R.A.; Hall, F.; Goetz, S.J. Importance of biomass in the global carbon cycle. J. Geophys. Res. 2009, 114, 1–13. [Google Scholar] [CrossRef]
- Lefsky, M.A.; Keller, M.; Pang, Y.; De Camargo, P.B.; Hunter, M.O. Revised method for forest canopy height estimation from geoscience laser altimeter system waveforms. J. Appl. Remote Sens. 2007, 1, 013537. [Google Scholar]
- Baghdadi, N.; Le Maire, G.; Bailly, J.-S.; Ose, K.; Nouvellon, Y.; Zribi, M.; Lemos, C.; Hakamada, R. Evaluation of ALOS/PALSAR L-band data for the estimation of eucalyptus plantations aboveground biomass in Brazil. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 3802–3811. [Google Scholar] [CrossRef] [Green Version]
- Le Toan, T.; Quegan, S.; Davidson, M.W.J.; Balzter, H.; Paillou, P.; Papathanassiou, K.; Ulander, L. The BIOMASS mission: Mapping global forest biomass to better understand the terrestrial carbon cycle. Remote Sens. Environ. 2011, 115, 2850–2860. [Google Scholar] [CrossRef] [Green Version]
- Healey, S.P.; Hernandez, M.W.; Edwards, D.P.; Lefsky, M.A.; Freeman, E.; Patterson, P.L.; Lindquist, E.J.; Lister, A.J. CMS: GLAS LiDAR-derived Global Estimates of Forest Canopy Height, 2004–2008; ORNL DAAC: Oak Ridge, TN, USA, 2015. [Google Scholar] [CrossRef]
- Goncalves, F.; Treuhaft, R.; Law, B.; Almeida, A.; Walker, W.; Baccini, A.; dos Santos, J.R.; Graca, P. Estimating aboveground biomass in tropical forests: Field methods and error analysis for the calibration of remote sensing observations. Remote Sens. 2017, 9, 47. [Google Scholar] [CrossRef]
- Martín-Neira, M. A passive reflectometry and interferometry system (PARIS): Application to ocean altimetry. ESA J. 1993, 17, 331–355. [Google Scholar]
- Li, W.; Rius, A.; Fabra, F.; Cardellach, E.; Ribó, S.; Martín-Neira, M. Revisiting the GNSS-R waveform statistics and its impact on altimetric retrievals. IEEE Trans. Geosci. Remote Sens. 2018, 56, 1229–1241. [Google Scholar] [CrossRef]
- Lowe, S.T.; LaBrecque, J.L.; Zuffada, C.; Romans, L.J.; Young, L.E.; Hajj, G.A. First spaceborne observation of an earth-reflected GPS signal. Radio Sci. 2002, 37, 7-1–7-28. [Google Scholar] [CrossRef]
- Gleason, S.; Hodgart, S.; Sun, Y.; Gommenginger, C.; Mackin, S.; Adjrad, M.; Unwin, M. Detection and processing of bistatically reflected GPS signals from a low Earth orbit for the purpose of ocean remote sensing. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1229–1241. [Google Scholar] [CrossRef] [Green Version]
- Unwin, M.; Jales, P.; Blunt, P.; Duncan, S. Preparation for the first flight of SSTL’s next generation space GNSS receivers. In Proceedings of the 6th ESA/European Workshop Satellite NAVITEC GNSS Signals Signal Processor, Noordwijk, The Netherlands, 5–7 December 2012; pp. 1–6. [Google Scholar]
- Carreno-Luengo, H.; Lowe, S.T.; Zuffada, C.; Esterhuizen, S.; Oveisgharan, S. Spaceborne GNSS-R from the SMAP mission: First assessment of polarimetric scatterometry over land and cryosphere. Remote Sens. 2017, 9, 362. [Google Scholar] [CrossRef] [Green Version]
- Ruf, C.S.; Atlas, R.; Chang, P.S.; Clarizia, M.P.; Garrison, J.L.; Gleason, S.; Katzberg, S.J.; Jelenak, Z.; Johnson, J.T.; Majumdar, S.J.; et al. New ocean winds satellite mission to probe hurricanes and tropical convection. Bull. Am. Meteorol. Soc. 2015, 97, 385–395. [Google Scholar] [CrossRef]
- Shah, R.; Xu, X.; Yueh, S.; Chae, C.S.; Elder, K.; Starr, B.; Kim, Y. Remote sensing of snow water equivalent using P-band coherent reflection. IEEE Geosci. Remote Sens. Lett. 2019, 14, 309–313. [Google Scholar] [CrossRef]
- Kim, H.; Lakshmi, V. Use of Cyclone Global Navigation Satellite System (CYGNSS) observations for estimation of soil moisture. Geophys. Res. Lett. 2018, 45, 8272–8282. [Google Scholar] [CrossRef] [Green Version]
- Carreno-Luengo, H.; Luzi, G.; Crosetto, M. Sensitivity of CyGNSS bistatic reflectivity and SMAP microwave radiometry brightness temperature to geophysical parameters over land surfaces. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 107–122. [Google Scholar] [CrossRef]
- Chew, C.; Small, E.; Podest, E. Monitoring land surface hydrology using CyGNSS. In Proceedings of the 2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 8309–8311. [Google Scholar]
- Chew, C.; Reager, J.T.; Small, E. CYGNSS data map flood inundation during the 2017 Atlantic hurricane season. Sci. Rep. 2018, 8, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Jensen, K.; McDonald, K.; Podest, E.; Rodriguez-Alvarez, N.; Horna, V.; Steiner, N. Assessing L-Band GNSS-Reflectometry and imaging radar for detecting sub-canopy inundation dynamics in a tropical wetlands complex. Remote Sens. 2018, 10, 1431. [Google Scholar] [CrossRef] [Green Version]
- Gerlein-Safdi, C.; Ruf, C. A CYGNSS-based algorithm for the detection of inland waterbodies. Geophys. Res. Lett. 2019, 46, 12065–12072. [Google Scholar] [CrossRef]
- Crespo, J.A.; Posselt, D.J.; Asharaf, S. CYGNSS Surface Heat Flux Product Development. Remote Sens. 2019, 11, 2294. [Google Scholar] [CrossRef] [Green Version]
- Liang, P.; Pierce, L.E.; Moghaddam, M. Radiative transfer model for microwave bistatic scattering from forests canopies. IEEE Trans. Geosci. Remote Sens. 2005, 43, 2470–2483. [Google Scholar] [CrossRef]
- Ferrazzoli, P.; Guerriero, L.; Pierdicca, N.; Rahmoune, R. Forest biomass monitoring with GNSS-R: Theoretical simulations. Adv. Space Res. 2011, 47, 1823–1832. [Google Scholar] [CrossRef]
- Wu, X.R.; Jin, S.G. GPS-Reflectometry: Forest canopies polarization scattering properties and modelling. Adv. Space Res. 2014, 54, 863–870. [Google Scholar] [CrossRef]
- Pierdicca, N.; Guerriero, L.; Giusto, R.; Brogioni, M.; Egido, A. SAVERS: A simulator of GNSS reflections from bare soil and vegetated soils. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 52, 6542–6554. [Google Scholar] [CrossRef]
- Egido, A. GNSS Refectometry for Land Remote Sensing Applications. Ph.D. Thesis, Universitat Politecnica de Catalunya (UPC), Barcelona, Spain, May 2013. [Google Scholar]
- Carreno-Luengo, H.; Camps, A.; Querol, J.; Forte, G. First results of a GNSS-R experiment from a stratospheric balloon over boreal forests. IEEE Trans. Geosci. Remote Sens. 2015, 54, 2652–2663. [Google Scholar] [CrossRef] [Green Version]
- Carreno-Luengo, H.; Amèzaga, A.; Vidal, D.; Olivé, R.; Munoz, J.-F.; Camps, A. First polarimetric GNSS-R measurements from a stratospheric flight over boreal forests. Remote Sens. 2015, 7, 13120–13138. [Google Scholar] [CrossRef] [Green Version]
- Kurum, M.; Deshpande, M.; Joseph, A.T.; O’Neill, P.E.; Lang, R.H.; Eroglu, O. ScCoBi-Veg: A generalized bistatic scattering model of reflectometry from vegetation for signals of opportunity applications. IEEE Trans. Geosci. Remote Sens. 2018, 57, 1049–1068. [Google Scholar] [CrossRef]
- Lindermayer, A. Developmental algorithms for multicellular organisms: A survey of L-systems. J. Theor. Bio. 1975, 54, 3–22. [Google Scholar] [CrossRef] [Green Version]
- Tsang, L.; Kong, J.A.; Shin, R.T. Theory of Microwave Remote Sensing; Wiley Interscience: New York, NY, USA, 1985. [Google Scholar]
- Zribi, M.; Guyon, D.; Motte, E.; Dayau, S.; Wigneron, J.-P.; Baghdadi, N.; Pierdicca, N. Performance of GNSS-R GLORI data for biomass estimation over the Landes forests. Elsevier Int. J. Earth Obs. Geoinf. 2019, 74, 150–158. [Google Scholar] [CrossRef]
- Motte, E.; Zribi, M.; Fanise, P.; Egido, A.; Darrozes, J.; Al-Yaari, A.; Baghdadi, N.; Baup, F.; Dayau, S.; Fieuzal, R.; et al. GLORI: A GNSS-R dual polarization airborne instrument for land surface monitoring. Sensors 2016, 16, 732. [Google Scholar] [CrossRef]
- Pierdicca, N.; Mollfulleda, A.; Constantini, F.; Guerriero, L.; Dente, L.; Paloscia, S.; Santi, E.; Zribi, M. Spaceborne GNSS Reflectometry data for land applications: An analysis of Techdemosat data. In Proceedings of the 2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 3343–3346. [Google Scholar]
- Santi, E.; Paloscia, S.; Pettinato, S.; Fontanelli, G.; Clarizia, M.-P.; Guerriero, L.; Pierdicca, N. Forest biomass estimate on local and global scales through GNSS reflectometry techniques. In Proceedings of the 2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 8680–8683. [Google Scholar]
- Ruf, C.; Cardellach, E.; Clarizia, M.-P.; Galdi, C.; Gleason, S.T.; Paloscia, S. Foreword to the special issue on Cyclone Global Navigation Satellite System (CYGNSS) early on orbit performance. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 3–6. [Google Scholar] [CrossRef]
- CYGNSS. CYGNSS Level 1 Science Data Record. Ver. 2.1. 2017. Available online: http://dx.doi.org/10.5067/CYGNS-L1X20 (accessed on 11 May 2019).
- Avitabile, V.; Herold, M.; Heuvelink, G.B.; Lewis, S.L.; Phillips, O.L.; Asner, G.P.; Armston, J.; Ashton, P.S.; Banin, L.; Bayol, N.; et al. An integrated pan-tropical biomass map using multiple reference datasets. Glob. Chang. Biol. 2016, 2, 1406–1420. [Google Scholar] [CrossRef] [Green Version]
- Zavorotny, V.U.; Voronovich, A.G. Scattering of GPS signals from the ocean with wind remote sensing applications. IEEE Trans. Geosci. Remote Sens. 2000, 38, 951–964. [Google Scholar] [CrossRef] [Green Version]
- Ulaby, F.T.; Long, D.G. Microwave Radar and Radiometric Remote Sensing, Univ; Michigan Press: Ann Arbor, MI, USA, 2014; p. 252. [Google Scholar]
- Pierdicca, N.; Guerriero, L.; Brogioni, M.; Egido, A. On the coherent and non-coherent components of bare soil and vegetated terrain bistatic scattering: Modelling the GNSS-R signal over land. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; pp. 3407–3410. [Google Scholar]
- Voronovich, A.G.; Zavorotny, V.U. Bistatic radar equation for signals of opportunity revisited. IEEE Trans. Geosci. Remote Sens. 2017, 56, 1959–1968. [Google Scholar] [CrossRef]
- Semmling, A.M.; Beckheinrich, J.; Wickert, J.; Beyerle, G.; Schön, S.; Fabra, F.; Pflug, H.; He, K.; Schwabe, J.; Scheinert, M. Sea surface topography retrieved from GNSS reflectometry phase data of the GEOHALO flight mission. Geophys. Res. Lett. 2014, 41, 954–960. [Google Scholar] [CrossRef] [Green Version]
- Martín, F.; Camps, A.; Park, H.; D’Addio, S.; Martín-Neira, M.; Pascual, D. Cross-correlation waveform analysis for conventional and interferometric GNSS-R approaches. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 1560–1572. [Google Scholar] [CrossRef]
- Carreno-Luengo, H.; Luzi, G.; Crosetto, M. Impact of the elevation angle on CyGNSS GNSS-R bistatic reflectivity as a function of effective surface roughness over land surfaces. Remote Sens. 2018, 10, 1749. [Google Scholar] [CrossRef] [Green Version]
- Camps, A.; Vall-llosera, M.; Park, H.; Portal, G.; Rossato, L. Sensitivity of TDS-1 reflectivity to soil moisture: Global and regional differences and impact of different spatial scales. Remote Sens. 2018, 10, 1856. [Google Scholar] [CrossRef] [Green Version]
- Vittucci, C.; Ferrazoli, P.; Kerr, Y.; Richaume, P.; Vaglio Laurin, G.; Guerriero, L. Analysis of vegetation optical depth and soil moisture retrieval by SMOS over tropical forests. IEEE Geosci. Remote Sens. Lett. 2018, 16, 504–508. [Google Scholar] [CrossRef]
- Konings, A.K.; Piles, M.; Das, N.; Entekhabi, D. L-band vegetation optical depth and effective scattering albedo estimation from SMAP. Remote Sens. Environ. 2017, 198, 460–470. [Google Scholar] [CrossRef]
- Clarizia, M.-P.; Ruf, C.; Cipollini, P.; Zuffada, C. First spaceborne observation of sea surface heightusing GPS-Reflectometry. AGU Geophys. Res. Lett. 2016, 43, 767–774. [Google Scholar] [CrossRef] [Green Version]
- Clarizia, M.-P.; Pierdicca, N.; Constantini, F.; Flouri, N. Analysis of CyGNSS data for soil moisture retrieval. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 2227–2235. [Google Scholar] [CrossRef]
- Wang, T.; Ruf, C.; Block, B.; McKague, D.S.; Gleason, S. Design and performance of a GPS constellation power monitor system for improved CYGNSS L1B calibration. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 26–36. [Google Scholar] [CrossRef]
- Said, F.; Jelenak, Z.; Chang, P.S.; Soisuvarn, S. An assessment of CYGNSS normalized bistatic radar cross section calibration. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 50–65. [Google Scholar] [CrossRef]
- Al-Khaldi, M.M.; Johnson, J.T.; O’Brien, A.; Balenzano, A.; Mattia, F. Time-series retrieval of soil moisture using CYGNSS. IEEE Trans. Geosci. Remote Sens. 2019, 57, 4322–4331. [Google Scholar] [CrossRef]
- Entekhabi, D.; Yueh, S.; O’Neill, P.E.; Kellogg, K.H.; Allen, A.; Bindlish, R.; Brown, M.; Chan, S.; Colliander, A.; Crow, W.T.; et al. SMAP Handbook. Soil Moisture Active Passive. Available online: https://nsidc.org/data/SPL3SMP_E/versions/1 (accessed on 4 April 2019).
- Chan, S.K.; Bindlish, R.; O’Neill, P.; Jackson, T.; Njoku, E.; Dunbar, S.; Chaubell, J.; Piepmeier, J.; Yueh, S.; Entekhabi, D.; et al. Development and assessment of the SMAP enhanced passive soil moisture product. Remote Sens. Environ. 2018, 204, 931–941. [Google Scholar] [CrossRef] [Green Version]
- O’Neill, P.; Chan, S.; Njoku, E.; Jackson, T.; Bindlish, R. Soil Moisture Active Passive (SMAP) Algorithm Theoretical Basis Document Level 2 & 3 Soil Moisture (Passive) Data Products. Revision C. Available online: https://nsidc.org/data/SPL3SMP_E/versions/1 (accessed on 16 April 2019).
- Rodriguez-Fernandez, N.J.; Mialon, A.; Mermoz, S.; Bouvet, A.; Richaume, P.; Al Bitar, A.; AlYaari, A.; Brandt, M.; Kaminski, T.; Le Toan, T.; et al. An evaluation of SMOS L-band vegetation optical depth (L-VOD) data sets: High sensitivity of L-VOD to aboveground biomass in Africa. Biogeosciences 2018, 15, 4627–4645. [Google Scholar] [CrossRef] [Green Version]
- Pampaloni, P. Microwave radiometry of forests. Waves Random Media 2004, 14, S275–S298. [Google Scholar] [CrossRef]
- Paloscia, S.; Pampaloni, P. Microwave polarization index for monitoring vegetation growth. IEEE Trans. Geosci. Remote Sens. 1988, 26, 617–621. [Google Scholar] [CrossRef]
- Santi, E.; Paloscia, S.; Pampaloni, P.; Pettinato, S.; Nomaki, T.; Seki, M.; Sekiya, K.; Maeda, T. Vegetation water content retrieval by means of multifrequency microwave acquisitions from AMSR2. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 3861–3873. [Google Scholar] [CrossRef]
- Paloscia, S.; Pampaloni, P.; Santi, E. Radiometric microwave indices for remote sensing of land surfaces. Remote Sens. 2018, 10, 1859. [Google Scholar] [CrossRef] [Green Version]
- Carreno-Luengo, H.; Luzi, G.; Crosetto, M. First evaluation of topography on GNSS-R: An empirical study based on a digital elevation model. Remote Sens. 2019, 11, 2556. [Google Scholar] [CrossRef] [Green Version]
- Amatulli, G.; Domisch, S.; Tuanmu, M.-N.; Parmentire, B.; Ranipeta, A.; Malczyk, J.; Jetz, W. A suite of global cross-scale topographic variables for environmental and biodiversity modelling. Nat. Sci. Data 2018, 5, 180040. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Villard, L.; Le Toan, T. Relating P-band SAR intensity to biomass for tropical dense forests in hilly terrain? IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 214–223. [Google Scholar] [CrossRef]
- Saatchi, S.S.; Harris, N.L.; Brown, S.; Lefsky, M.; Mitchard, E.T.; Salas, W.; Zutta, B.R.; Buermann, W.; Lewis, S.L.; Hagen, S.; et al. Benchmark map of forest carbon stocks in tropical regions across three continents. Natl. Acad. Sci. USA 2011, 108, 9899–9904. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Baccini, A.G.S.J.; Goetz, S.J.; Walker, W.S.; Laporte, N.T.; Sun, M.; Sulla-Menashe, D.; Hackler, J.; Beck, P.S.A.; Dubayah, R.; Friedl, M.A.; et al. Estimated carbon dioxide emissions from tropical deforestation improved by carbon-density maps. Nat. Clim. Chang. 2012, 2, 182–185. [Google Scholar] [CrossRef]
- Yu, Y.; Saatchi, S. Sensitivity of L-band SAR backscatter to aboveground biomass of global forests. Remote Sens. 2016, 8, 522. [Google Scholar] [CrossRef] [Green Version]
- D’Addio, S.; Buck, C.; Martin-Neira, M. PARIS altimetry precision prediction with Galileo signals-in-space. In Proceedings of the2008 IEEE International Geoscience and Remote Sensing Symposium, Boston, MA, USA, 7–11 July 2008; p. III-63. [Google Scholar]
- Vittucci, C.; Vaglio Laurin, G.; Tramontana, G.; Ferrazoli, P.; Guerriero, L.; Papale, D. Vegetation optical depth at L-band and above ground biomass in the tropical range: Evaluating their relationships at continental and regional scales. Elsevier Int. J. Appl. Earth Obs. Geoinf. 2019, 19, 151–161. [Google Scholar] [CrossRef]
- Newman, A. Tropical Rainforest: Our Most Valuable and Endangered Habitat with a Blueprint for Its Survival into the Third Millennium, 2nd ed.; Checkmark Books: New York, USA, 2000; ISBN 0816039739. [Google Scholar]
- Dryland and Dryland with Forests. Available online: https://earthobservatory.nasa.gov/IOTD/view.php?id=90635 (accessed on 2 January 2019).
- Tropical and Subtropical Coniferous Forests. Available online: https://www.worldwildlife.org/biomes/tropical-and-subtropical-coniferous-forests (accessed on 1 January 2020).
- Tropical and Subtropical Dry Broadleaf Forest Ecoregions. Available online: https://web.archive.org/web/20120425205410/http://wwf.panda.org/about_our_earth/ecoregions/about/habitat_types/selecting_terrestrial_ecoregions/habitat02.cfm (accessed on 20 January 2020).
- The Congo Basin Forest. Available online: https://globalforestatlas.yale.edu/region/congo (accessed on 20 January 2020).
- The Amazon Basin Forest. Available online: https://globalforestatlas.yale.edu/region/amazon (accessed on 20 January 2020).













| ~[80, 90]° | ~[60, 70]° | |||||||||||||||
| r | RMSE [ton/ha] | O | Slope [(ton/ha)/m] | r | RMSE [ton/ha] | O | Slope [(ton/ha)/dB] | r | RMSE [ton/ha] | O | Slope [(ton/ha)/m] | r | RMSE [ton/ha] | O | Slope [(ton/ha)/dB] | |
| CG | 0.73 | 40.6 | 3 | - | −0.78 | 26.8 | 4 | - | 0.91 | 31.5 | 3 | - | −0.92 | 29.8 | 4 | - |
| AM | 0.75 | 33.7 | 4 | - | −0.93 | 13.5 | 4 | - | 0.68 | 26.6 | 6 | - | −0.88 | 13.6 | 6 | - |
| CF | 0.36 | 12.2 | 1 | 0.0131 | −0.69 | 6.8 | 1 | −1.1201 | 0.34 | 9.2 | 1 | 0.0112 | −0.67 | 8.4 | 1 | −1.0972 |
| DR | 0.38 | 11.4 | 1 | 0.0164 | −0.62 | 7.6 | 1 | −1.3260 | 0.53 | 12.3 | 1 | 0.0176 | −0.67 | 5.6 | 1 | −1.3675 |
| MT | 0.25 | 5 | 1 | 0.0087 | −0.26 | 5.3 | 1 | −0.2802 | 0.10 | 3.9 | 1 | 0.0035 | −0.43 | 4.2 | 1 | −0.4402 |
| ~[40, 50]° | ~[20, 30]° | |||||||||||||||
| r | RMSE [ton/ha] | O | Slope [(ton/ha)/m] | r | RMSE [ton/ha] | O | Slope [(ton/ha)/dB] | r | RMSE [ton/ha] | O | Slope [(ton/ha)/m] | r | RMSE [ton/ha] | O | Slope [(ton/ha)/dB] | |
| CG | 0.89 | 33.4 | 3 | - | −0.65 | 24.1 | 4 | - | 0.89 | 40.1 | 5 | - | −0.66 | 41.2 | 4 | - |
| AM | 0.84 | 24.6 | 4 | - | −0.82 | 16.6 | 4 | - | 0.90 | 18.4 | 4 | - | −0.93 | 16.9 | 4 | - |
| CG | 0.25 | 8.6 | 1 | 0.0085 | −0.64 | 6.7 | 1 | −1.0194 | 0.11 | 5.9 | 1 | 0.0026 | 0.34 | 9.9 | 1 | −1.0666 |
| DR | 0.47 | 7.5 | 1 | 0.0173 | −0.66 | 6.3 | 1 | −1.1877 | 0.20 | 7.1 | 1 | 0.0080 | 0 | 6.7 | 1 | 0.0452 |
| MT | 0.40 | 4.3 | 1 | 0.0108 | −0.55 | 4.7 | 1 | −0.6470 | 0.36 | 3.8 | 1 | 0.0078 | −0.53 | 3.7 | 1 | −0.6118 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carreno-Luengo, H.; Luzi, G.; Crosetto, M. Above-Ground Biomass Retrieval over Tropical Forests: A Novel GNSS-R Approach with CyGNSS. Remote Sens. 2020, 12, 1368. https://doi.org/10.3390/rs12091368
Carreno-Luengo H, Luzi G, Crosetto M. Above-Ground Biomass Retrieval over Tropical Forests: A Novel GNSS-R Approach with CyGNSS. Remote Sensing. 2020; 12(9):1368. https://doi.org/10.3390/rs12091368
Chicago/Turabian StyleCarreno-Luengo, Hugo, Guido Luzi, and Michele Crosetto. 2020. "Above-Ground Biomass Retrieval over Tropical Forests: A Novel GNSS-R Approach with CyGNSS" Remote Sensing 12, no. 9: 1368. https://doi.org/10.3390/rs12091368
APA StyleCarreno-Luengo, H., Luzi, G., & Crosetto, M. (2020). Above-Ground Biomass Retrieval over Tropical Forests: A Novel GNSS-R Approach with CyGNSS. Remote Sensing, 12(9), 1368. https://doi.org/10.3390/rs12091368