A Synthetic Quantitative Precipitation Estimation by Integrating S- and C-Band Dual-Polarization Radars over Northern Taiwan
Abstract
:1. Introduction
2. Quality Control Procedures for S- and C-Band Dual-Polarization Radars
2.1. PBB Removal
2.2. Non-Meteorological Signal Removal
2.3. Attenuation Correction
2.4. ZHH Systematic Bias and the WRE Correction
2.5. ZDR Systematic Bias Correction
3. Quantitative Precipitation Estimation from S- and C-Band Dual-Polarization Radars
3.1. Disdrometer Data
3.2. QPE Coefficients
3.3. Simplified Decision-Tree QPE
3.4. Integration Methods for Radar-Based QPE
4. QPE Comparison between C- and S-Band Radar
4.1. The Influence of QC Procedures on C- and S-Band QPE
4.2. C- and S-Band Seasonal and All-Season Coefficients in QPE Algorithms
4.3. C- and S-Band Discrete QPE Comparison (D-QPE)
4.4. Discretely Combined C- and S-Band QPEs (DC-QPE)
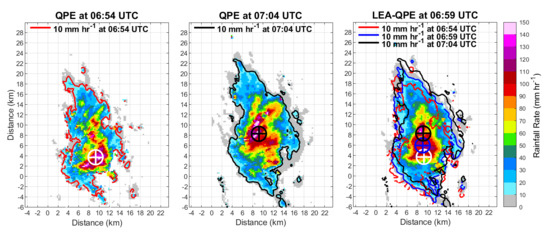
4.5. Lagrangian-Evolution Adjustment (LEA) QPE
5. Summary
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Marshall, J.S.; Palmer, W.M.K. The distribution of raindrops with size. J. Meteorol. 1948, 5, 165–166. [Google Scholar] [CrossRef]
- Radar observation of the atmosphere. L. J. Battan (The University of Chicago Press) 1973. PP X, 324; 125 figures, 21 tables. £7·15. Q. J. R. Meteorol. Soc. 1973, 99, 793. [CrossRef]
- Seliga, T.A.; Bringi, V.N. Potential Use of Radar Differential Reflectivity Measurements at Orthogonal Polarizations for Measuring Precipitation. J. Appl. Meteorol. 1976, 15, 69–76. [Google Scholar] [CrossRef] [Green Version]
- Seliga, T.A.; Bringi, V.N.; Al-Khatib, H.H. A Preliminary Study of Comparative Measurements of Rainfall Rate Using the Differential Reflectivity Radar Technique and a Raingage Network. J. Appl. Meteorol. 1981, 20, 1362–1368. [Google Scholar] [CrossRef] [Green Version]
- Gorgucci, E.; Chandrasekar, V.; Scarchilli, G. Radar and Surface Measurement of Rainfall during CaPE: 26 July 1991 Case Study. J. Appl. Meteorol. 1995, 34, 1570–1577. [Google Scholar] [CrossRef]
- Gorgucci, E.; Scarchilli, G.; Chandrasekar, V. Specific Differential Phase Estimation in the Presence of Nonuniform Rainfall Medium along the Path. J. Atmos. Ocean. Technol. 1999, 16, 1690–1697. [Google Scholar] [CrossRef]
- Ryzhkov, A.V.; Zrnić, D.S. Comparison of Dual-Polarization Radar Estimators of Rain. J. Atmos. Ocean. Technol. 1995, 12, 249–256. [Google Scholar] [CrossRef] [Green Version]
- Ryzhkov, A.V.; Giangrande, S.E.; Schuur, T.J. Rainfall Estimation with a Polarimetric Prototype of WSR-88D. J. Appl. Meteorol. 2005, 44, 502–515. [Google Scholar] [CrossRef] [Green Version]
- Ryzhkov, A.V.; Schuur, T.J.; Burgess, D.W.; Heinselman, P.L.; Giangrande, S.E.; Zrnic, D.S. The Joint Polarization Experiment: Polarimetric rainfall measurements and hydrometeor classification. Bull. Am. Meteorol. Soc. 2005, 86, 809–824. [Google Scholar] [CrossRef] [Green Version]
- Fulton, R.A.; Breidenbach, J.P.; Seo, D.; Miller, D.A.; O’Bannon, T. The WSR-88D rainfall algorithm. Weather Forecast. 1998, 13, 377–395. [Google Scholar] [CrossRef]
- Bringi, V.N.; Chandrasekar, V. Polarimetric Doppler Weather Radar: Principles and Application; Cambridge University Press: Cambridge, UK, 2001; 636p. [Google Scholar]
- Illingworth, A.J.; Thompson, R.J. The Estimation of Moderate Rain Rates with Operational Polarisation Radar. In Proceedings of the 32th Conference on Radar Meteorology, Albuquerque, NM, USA, 22–29 October 2005. [Google Scholar]
- Hogan, R.J. A Variational Scheme for Retrieving Rainfall Rate and Hail Reflectivity Fraction from Polarization Radar. J. Appl. Meteorol. Climatol. 2007, 46, 1544–1564. [Google Scholar] [CrossRef] [Green Version]
- Giangrande, S.E.; Ryzhkov, A.V. Estimation of Rainfall Based on the Results of Polarimetric Echo Classification. J. Appl. Meteorol. Climatol. 2008, 47, 2445–2462. [Google Scholar] [CrossRef]
- Ventura, J.F.; Kabeche, F.; Fradon, B.; Hogan, R.; Boumahmoud, A.A.; Illingworth, A.; Tabary, P. Extensive evaluation of Polarimetric Quantitative Precipitation Estimations (QPE) in ideal and less ideal conditions. In Proceedings of the 6th European Conference on Radar in Meteorology and Hydrology, Sibiu, Romania, 6–10 September 2010. [Google Scholar]
- Cifelli, R.; Chandrasekar, V.; Lim, S.; Kennedy, P.C.; Wang, Y.; Rutledge, S.A. A New Dual-Polarization Radar Rainfall Algorithm: Application in Colorado Precipitation Events. J. Atmos. Ocean. Technol. 2011, 28, 352–364. [Google Scholar] [CrossRef] [Green Version]
- Chen, H.; Chandrasekar, V. The quantitative precipitation estimation system for Dallas–Fort Worth (DFW) urban remote sensing network. J. Hydrol. 2015, 531, 259–271. [Google Scholar] [CrossRef] [Green Version]
- Kwon, S.; Jung, S.H.; Lee, G. Inter-comparison of radar rainfall rate using Constant Altitude Plan Position Indicator and hybrid surface rainfall maps. J. Hydrol. 2015, 531, 234–247. [Google Scholar] [CrossRef]
- Chang, W.; Vivekanandan, J.; Ikeda, K.; Lin, P. Quantitative Precipitation Estimation of the Epic 2013 Colorado Flood Event: Polarization Radar-Based Variational Scheme. J. Appl. Meteorol. Climatol. 2016, 55, 1477–1495. [Google Scholar] [CrossRef]
- Ryzhkov, A.V.; Diederich, M.; Zhang, P.; Simmer, C. Potential utilization of specific attenuation for rainfall estimation, mitigation of partial beam blockage, and radar networking. J. Atmos. Ocean. Technol. 2014, 31, 599–619. [Google Scholar] [CrossRef]
- Diederich, M.; Ryzhkov, A.; Simmer, C.; Zhang, P.; Trömel, S. Use of specific attenuation for rainfall measurement at X-band radar wavelengths. Part I: Radar calibration and partial beam blockage estimation. J. Hydrometeorol. 2015, 16, 487–502. [Google Scholar] [CrossRef]
- Diederich, M.; Ryzhkov, A.; Simmer, C.; Zhang, P.; Trömel, S. Use of specific attenuation for rainfall measurement at X-band radar wavelengths. Part II: Rainfall estimates and comparison with rain gauges. J. Hydrometeorol. 2015, 16, 503–516. [Google Scholar] [CrossRef]
- Wang, Y.; Cocks, S.; Tang, L.; Ruzhkov, A.; Zhang, P.; Zhang, J.; Howard, K. A prototype quantitative precipitation estimation algorithm for operational S-Band polarimetric radar utilizing specific attenuation and specific differential phase. Part I: Algorithm description. J. Hydrometeorol. 2019, 20, 985–997. [Google Scholar] [CrossRef]
- Zhang, J.; Tang, L.; Cocks, S.; Zhang, P.; Ryzhkov, A.; Howard, K.; Langston, C.; Kaney, B. A Dual-polarization Radar Synthetic QPE for Operations. J. Hydrometeorol. 2020, 21, 2507–2521. [Google Scholar] [CrossRef] [Green Version]
- Ruzanski, E.; Chandrasekar, V. Nowcasting Rainfall Fields Derived from Specific Differential Phase. J. Appl. Meteorol. Climatol. 2012, 51, 1950–1959. [Google Scholar] [CrossRef]
- Chang, W.; Vivekanandan, J.; Chen Wang, T. Estimation of X-Band Polarimetric Radar Attenuation and Measurement Uncertainty Using a Variational Method. J. Appl. Meteor. Climatol. 2014, 53, 1099–1119. [Google Scholar] [CrossRef]
- Lee, G.W. Sources of Errors in Rainfall Measurements by Polarimetric Radar: Variability of Drop Size Distributions, Observational Noise, and Variation of Relationships between R and Polarimetric Parameters. J. Atmos. Ocean. Technol. 2006, 23, 1005–1028. [Google Scholar] [CrossRef]
- Melnikov, V.M. Simultaneous Transmission Mode for the Polarimetric WSR-88D; NOAA/NSSL Report. 2004; 84p. Available online: http://www.nssl.noaa.gov/publications/wsr88d_reports/SHV_statistics.pdf (accessed on 1 June 2018).
- Chang, P.-L.; Zhang, J.; Tang, Y.-S.; Tang, L.; Lin, P.-F.; Langston, C.; Kaney, B.; Chen, C.-R.; Howard, K. An Operational Multi-Radar Multi-Sensor QPE System in Taiwan. Bull. Am. Meteorol. Soc. 2020. [Google Scholar] [CrossRef]
- Wolff, D.B.; Petersen, W.A.; Tokay, A.; Marks, D.A.; Pippitt, J.L. Assessing Dual-Polarization Radar Estimates of Extreme Rainfall during Hurricane Harvey. J. Atmos. Ocean. Technol. 2019, 36, 2501–2520. [Google Scholar] [CrossRef]
- Chang, W.-Y.; Wang, T.-C.-C.; Lin, P.-L. Characteristics of the raindrop size distribution and drop shape relation in typhoon systems in the western Pacific from the 2D video disdrometer and NCU C-band polarimetric radar. J. Atmos. Ocean. Technol. 2009, 26, 1973–1993. [Google Scholar] [CrossRef]
- Lee, M.-T.; Lin, P.-L.; Chang, W.-Y.; Seela, B.K.; Janapati, J. Microphysical characteristics and types of precipitation for different seasons over north Taiwan. J. Meteorol. Soc. Jpn. 2019, 97, 841–865. [Google Scholar] [CrossRef] [Green Version]
- Chang, P.-L.; Lin, P.-F.; Jou, J.-D.B.; Zhang, J. An application of reflectivity climatology in constructing radar hybrid scans over complex terrain. J. Atmos. Ocean. Technol. 2009, 26, 1315–1327. [Google Scholar] [CrossRef]
- O’Bannon, T. Using a ‘terrain-based’ hybrid scan to improve WSR-88D precipitation estimates. In Proceedings of the 28th Conference on Radar Meteorology, Austin, TX, USA, 7–12 September 1997; American Meteorology Society: Boston, MA, USA, 1997; pp. 506–507. [Google Scholar]
- Maddox, R.A.; Zhang, J.; Gourley, J.J.; Howard, K.W. Weather radar coverage over the contiguous United States. Weather Forecast. 2002, 17, 927–934. [Google Scholar] [CrossRef]
- Vivekanandan, J.; Zhang, G.; Ellis, S.M.; Rajopadhyaya, D.; Avery, S.K. Radar reflectivity calibration using differential propagation phase measurement. Radio Sci. 2003, 38, 14-1–14-14. [Google Scholar] [CrossRef] [Green Version]
- Gorgucci, E.; Bechini, R.; Baldini, L.; Cremonini, R.; Chandrasekar, V. The Influence of Antenna Radome on Weather Radar Calibration and Its Real-Time Assessment. J. Atmos. Ocean. Technol. 2013, 30, 676–689. [Google Scholar] [CrossRef]
- Frasier, S.J.; Kabeche, F.; Figueras i Ventura, J.; Al-Sakka, H.; Tabary, P.; Beck, J.; Bousquet, O. In-Place Estimation of Wet Radome Attenuation at X Band. J. Atmos. Ocean. Technol. 2013, 30, 917–928. [Google Scholar] [CrossRef]
- Salazar-Cerreño, J.L.; Chandrasekar, V.; Trabal, J.M.; Siquera, P.; Medina, R.; Knapp, E.; McLaughlin, D.J. A Drop Size Distribution (DSD)-Based Model for Evaluating the Performance of Wet Radomes for Dual-Polarized Radars. J. Atmos. Ocean. Technol. 2014, 31, 2409–2430. [Google Scholar] [CrossRef]
- Mancini, A.; Salazar, J.L.; Lebrón, R.M.; Cheong, B.L. A Novel Instrument for Real-Time Measurement of Attenuation of Weather Radar Radome Including Its Outer Surface. Part I: The Concept. J. Atmos. Ocean. Technol. 2018, 35, 953–973. [Google Scholar] [CrossRef]
- Mancini, A.; Salazar, J.L.; Lebrón, R.M.; Cheong, B.L. A Novel Instrument for Real-Time Measurement of Attenuation of Weather Radar Radome Including Its Outer Surface. Part II: Applications. J. Atmos. Ocean. Technol. 2018, 35, 975–991. [Google Scholar] [CrossRef]
- Schönhuber, M.; Urban, H.E.; Poiares Baptista, P.P.V.; Randeu, W.L.; Riedler, W. Weather radar versus 2D-video-disdrometer data. In Weather Radar Technology for Water Resources Management; Bragg, B., Jr., Massambani, O., Eds.; UNESCO Press: Paris, France, 1997; pp. 159–171. [Google Scholar]
- Kruger, A.; Krajewski, W.F. Two-dimensional video disdrometer: A description. J. Atmos. Ocean. Technol. 2002, 19, 602–617. [Google Scholar] [CrossRef]
- Thurai, M.; Bringi, V.N. Drop axis ratios from 2D video disdrometer. J. Atmos. Ocean. Technol. 2005, 22, 966–978. [Google Scholar] [CrossRef]
- Smith, P.L.; Kliche, D.V. The Bias in moment estimators for parameters of drop size distribution functions: Sampling from exponential distributions. J. Appl. Meteorol. 2005, 44, 1195–1205. [Google Scholar] [CrossRef]
- Chen, C.S.; Chen, Y.L. The rainfall characteristics of Taiwan. Mon. Weather Rev. 2003, 131, 1323–1341. [Google Scholar] [CrossRef]
- Barber, P.; Yeh, C. Scattering of electromagnetic waves by arbitrarily shaped dielectric bodies. Appl. Opt. 1975, 14, 2864–2872. [Google Scholar] [CrossRef] [PubMed]
- Brandes, E.A.; Zhang, G.; Vivekanandan, J. Experiments in rainfall estimation with a polarimetric radar in a subtropical environment. J. Appl. Meteorol. 2002, 41, 674–685. [Google Scholar] [CrossRef] [Green Version]
- Rodgers, C.D. Inverse Methods for Atmospheric Soundings: Theory and Practice; World Scientific Co. Pte. Ltd.: Singapore, 2000; 256p. [Google Scholar] [CrossRef]
- Hubbert, J.; Chandrasekar, V.; Bringi, V.N.; Meischner, P. Processing and interpretation of coherent dual-polarized radar measurements. J. Atmos. Ocean. Technol. 1993, 10, 155–164. [Google Scholar] [CrossRef] [Green Version]
- Hubbert, J.; Bringi, V.N. An iterative filtering technique for the analysis of copolar differential phase and dual- frequency radar measurements. J. Atmos. Ocean. Technol. 1995, 12, 643–648. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Chandrasekar, V. Algorithm for estimation of the specific differential phase. J. Atmos. Ocean. Technol. 2009, 26, 2565–2578. [Google Scholar] [CrossRef]
- Giangrande, S.E.; McGraw, R.; Lei, L. An application of linear programming to polarimetric radar differential phase processing. J. Atmos. Ocean. Technol. 2013, 30, 1716–1729. [Google Scholar] [CrossRef]
- Cifelli, R.; Petersen, W.A.; Carey, L.D.; Rutledge, S.A.; da Silva Dias, M.A.F. Radar observations of the kinematic, microphysical, and precipitation characteristics of two MCSs in TRMM LBA. J. Geophys. Res. Atmos. 2002, 107, 8077. [Google Scholar] [CrossRef] [Green Version]
- Rinehart, R.E.; Garvey, E.T. Three-dimensional storm motion detection by conventional weather radar. Nature 1978, 273, 287–289. [Google Scholar] [CrossRef]













| RCWF | NCU C-POL | |
|---|---|---|
| Wavelength (cm) | 10.7 | 5.3 |
| Location (degree) | 121.77 N 25.07 E | 212.18 N 24.97 E |
| Height (m) | 766 | 156 |
| Range resolution (m) | 250 | 250 |
| Beam resolution (degree) | 0.5 | 1 |
| All-Season | Spring | Mei-Yu | Summer Convection | Typhoon | Winter Cold Front | ||
|---|---|---|---|---|---|---|---|
| R(ZHH) | a1 | 0.0279 | 0.0197 | 0.0244 | 0.0435 | 0.0282 | 0.0408 |
| b1 | 0.6619 | 0.6874 | 0.6779 | 0.6233 | 0.6624 | 0.6173 | |
| R(ZHH,ZDR) | a2 | 0.0046 | 0.0019 | 0.0018 | 0.0011 | 0.0013 | 0.0033 |
| b2 | 0.8492 | 0.9452 | 0.9578 | 1.0017 | 0.9490 | 0.8888 | |
| c2 | −0.6193 | −0.9734 | −1.0434 | −1.1240 | −0.7988 | −0.7439 | |
| R(KDP) | a3 | 47.5998 | 44.6864 | 48.0516 | 48.3448 | 64.3293 | 42.5163 |
| b3 | 0.7605 | 0.7950 | 0.7915 | 0.7725 | 0.7278 | 0.7225 | |
| R(KDP,ZDR) | a4 | 64.8411 | 61.9421 | 62.3633 | 63.3633 | 73.0964 | 60.2012 |
| b4 | 0.9880 | 0.9782 | 0.9727 | 0.9727 | 0.9476 | 0.9486 | |
| c4 | −0.6921 | −0.6445 | −0.6196 | −0.6196 | −0.6039 | −0.5836 |
| All-Season | Spring | Mei-Yu | Summer Convection | Typhoon | Winter Cold Front | ||
|---|---|---|---|---|---|---|---|
| R(ZHH) | a1 | 0.0376 | 0.0260 | 0.0316 | 0.0710 | 0.0360 | 0.0434 |
| b1 | 0.6340 | 0.6330 | 0.6558 | 0.5761 | 0.6394 | 0.6138 | |
| R(ZHH,ZDR) | a2 | 0.0035 | 0.0014 | 0.0014 | 0.0013 | 0.0010 | 0.0028 |
| b2 | 0.8886 | 0.9922 | 0.9952 | 1.0018 | 0.9812 | 0.9199 | |
| c2 | −0.6575 | −0.9840 | −1.0031 | −1.0239 | −0.7714 | −0.7474 | |
| R(KDP) | a3 | 26.2343 | 23.9480 | 25.8619 | 26.4884 | 36.1670 | 24.0925 |
| b3 | 0.7485 | 0.7823 | 0.7784 | 0.7590 | 0.7158 | 0.7103 | |
| R(KDP,ZDR) | a4 | 31.2514 | 29.8459 | 30.4106 | 29.9747 | 36.8965 | 30.3301 |
| b4 | 0.9648 | 0.9563 | 0.9593 | 0.9381 | 0.9212 | 0.9500 | |
| c4 | −0.5988 | −0.5334 | −0.5418 | −0.5132 | −0.5146 | −0.5717 |
| Date (hour) | Precipitation Type | Max. Hourly Rainfall (mm h−1)/Accumulated Rainfall (mm) | Scan Time (min:s) | |
|---|---|---|---|---|
| RCWF | NCU C-POL | |||
| 26 April 2014 (1 h) | Spring | 60 | 5:50 | 6:40 |
| 5 May 2014 (2 h) | Mei-Yu | 20/33 | 5:50 | 6:40 |
| 9 May 2014 (2 h) | Mei-Yu | 23.5/35 | 5:50 | 6:40 |
| 15 May 2014 (1 h) | Mei-Yu | 57.5 | 5:50 | 6:40 |
| 20 May 2014 (3 h) | Mei-Yu | 26/50 | 5:50 | 6:40 |
| 21 May 2014 (2 h) | Mei-Yu | 38/52.5 | 5:50 | 6:40 |
| 29 May 2014 (6 h) | Mei-Yu | 56.5/115 | 5:50 | 6:40 |
| 5 June 2014 (6 h) | Mei-Yu | 46/135.5 | 5:50 | 6:40 |
| 7 June 2014 (1 h) | Mei-Yu | 35 | 5:50 | 6:40 |
| 31 July 2014 (1 h) | Summer convection | 48.5 | 5:50 | 10:00 |
| 13 August 2014 (1 h) | Summer convection | 36.5 | 5:50 | 10:00 |
| 19 August 2014 (3 h) | Summer convection | 71.5/92.5 | 5:50 | 10:00 |
| 24 February 2015 (4 h) | Cold front | 29.5/58.5 | 5:50 | 10:00 |
| 12 May 2015 (2 h) | Mei-Yu | 41.5/50.5 | 5:50 | 10:00 |
| 22 May 2015 (2 h) | Mei-Yu | 19.5/28 | 5:50 | 10:00 |
| 6 June 2015 (2 h) | Mei-Yu | 37/45.5 | 5:50 | 10:00 |
| 14 June 2015 (2 h) | Mei-Yu | 103.5/167 | 5:50 | 10:00/12:30 |
| 23 July 2015 (2 h) | Summer convection | 74/80 | 5:50 | 10:00/12:30 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.-Y.; Chang, W.-Y.; Chang, P.-L. A Synthetic Quantitative Precipitation Estimation by Integrating S- and C-Band Dual-Polarization Radars over Northern Taiwan. Remote Sens. 2021, 13, 154. https://doi.org/10.3390/rs13010154
Chen J-Y, Chang W-Y, Chang P-L. A Synthetic Quantitative Precipitation Estimation by Integrating S- and C-Band Dual-Polarization Radars over Northern Taiwan. Remote Sensing. 2021; 13(1):154. https://doi.org/10.3390/rs13010154
Chicago/Turabian StyleChen, Ju-Yu, Wei-Yu Chang, and Pao-Liang Chang. 2021. "A Synthetic Quantitative Precipitation Estimation by Integrating S- and C-Band Dual-Polarization Radars over Northern Taiwan" Remote Sensing 13, no. 1: 154. https://doi.org/10.3390/rs13010154
APA StyleChen, J. -Y., Chang, W. -Y., & Chang, P. -L. (2021). A Synthetic Quantitative Precipitation Estimation by Integrating S- and C-Band Dual-Polarization Radars over Northern Taiwan. Remote Sensing, 13(1), 154. https://doi.org/10.3390/rs13010154