Ka-Band Radar Cross-Section of Breaking Wind Waves
Abstract
:1. Introduction
2. Data and Methods
2.1. Experiment and Instruments
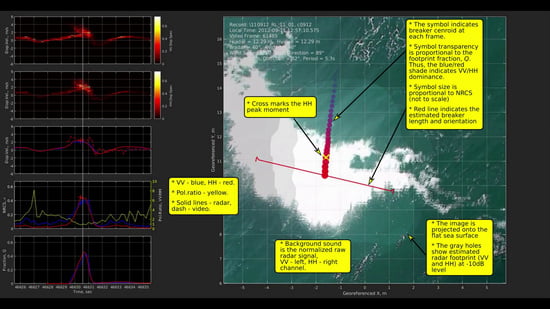
2.2. Radar Data Processing
2.3. Video Data Processing
3. Results
3.1. NRCS Versus Whitecap Fraction
3.2. Background Estimation
3.3. Whitecap NRCS
3.4. Comparison with Models
4. Discussion
4.1. Breaker Radar Model
4.2. Comparison with the Measurements
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Valenzuela, G.R. Theories for the interaction of electromagnetic and ocean waves—A review. Bound.-Layer Meteorol. 1978, 13, 61–85. [Google Scholar] [CrossRef]
- Elfouhaily, T.M.; Guérin, C.A. TOPICAL REVIEW: A critical survey of approximate scattering wave theories from random rough surfaces. Waves Random Media 2004, 14, 1. [Google Scholar] [CrossRef]
- Kanevsky, M.B. Radar Imaging of the Ocean Waves; Elsevier: Amsterdam, The Netherlands, 2009. [Google Scholar] [CrossRef]
- Chapron, B.; Kerbaol, V.; Vandemark, D.; Elfouhaily, T. Importance of peakedness in sea surface slope measurements and applications. J. Geophys. Res. Oceans 2000, 105, 17195–17202. [Google Scholar] [CrossRef] [Green Version]
- Chapron, B.; Johnsen, H.; Garello, R. Wave and wind retrieval from sar images of the ocean. Ann. Télécommun. 2001, 56, 682–699. [Google Scholar] [CrossRef]
- Voronovich, A.G.; Zavorotny, V.U. Theoretical model for scattering of radar signals in Ku- and C-bands from a rough sea surface with breaking waves. Waves Random Media 2001, 11, 247–269. [Google Scholar] [CrossRef]
- Chapron, B.; Vandemark, D.; Elfouhaily, T. On the skewness of the sea slope probability distribution. In Gas Transfer at Water Surface; Donelan, M.A., Drennan, W.M., Saltzman, E.S., Wanninkhof, R., Eds.; AGU: Washington, DC, USA, 2002; Volume 127, pp. 59–63. [Google Scholar] [CrossRef] [Green Version]
- Mouche, A.A.; Chapron, B.; Reul, N.; Hauser, D.; Quilfen, Y. Importance of the sea surface curvature to interpret the normalized radar cross section. J. Geophys. Res. Oceans 2007, 112, 10002. [Google Scholar] [CrossRef] [Green Version]
- Walsh, E.J.; Wright, C.W.; Banner, M.L.; Vandemark, D.C.; Chapron, B.; Jensen, J.; Lee, S. The Southern Ocean Waves Experiment. Part III: Sea Surface Slope Statistics and Near-Nadir Remote Sensing. J. Phys. Oceanogr. 2008, 38, 670–685. [Google Scholar] [CrossRef]
- Kudryavtsev, V.; Hauser, D.; Caudal, G.; Chapron, B. A semiempirical model of the normalized radar cross-section of the sea surface 1. Background model. J. Geophys. Res. Oceans 2003, 108, FET 2-1–FET 2-24. [Google Scholar] [CrossRef] [Green Version]
- Hansen, M.W.; Kudryavtsev, V.; Chapron, B.; Johannessen, J.A.; Collard, F.; Dagestad, K.F.; Mouche, A.A. Simulation of radar backscatter and Doppler shifts of wave-current interaction in the presence of strong tidal current. Remote Sens. Environ. 2012, 120, 113–122. [Google Scholar] [CrossRef] [Green Version]
- Kalmykov, A.I.; Pustovoytenko, V.V. On polarization features of radio signals scattered from the sea surface at small grazing angles. J. Geophys. Res. 1976, 81, 1960–1964. [Google Scholar] [CrossRef]
- Plant, W.J. The Modulation Transfer Function: Concept and Applications. In Radar Scattering from Modulated Wind Waves; Komen, G.J., Oost, W.A., Eds.; Springer: Dordrecht, The Netherlands, 1989; pp. 155–172. [Google Scholar] [CrossRef]
- Keller, W.C.; Plant, W.J.; Petitt, R.A.; Terray, E.A. Microwave backscatter from the sea: Modulation of received power and Doppler bandwidth by long waves. J. Geophys. Res. Oceans 1994, 99, 9751–9766. [Google Scholar] [CrossRef]
- Kudryavtsev, V.; Hauser, D.; Caudal, G.; Chapron, B. A semiempirical model of the normalized radar cross section of the sea surface, 2. Radar modulation transfer function. J. Geophys. Res. Oceans 2003, 108, FET 3-1–FET 3-16. [Google Scholar] [CrossRef]
- Hwang, P.A.; Sletten, M.A.; Toporkov, J.V. Breaking wave contribution to low grazing angle radar backscatter from the ocean surface. J. Geophys. Res. Oceans 2008, 113. [Google Scholar] [CrossRef]
- Malinovsky, V.V.; Korinenko, A.E.; Kudryavtsev, V.N. Empirical Model of Radar Scattering in the 3-cm Wavelength Range on the Sea at Wide Incidence Angles. Radiophys. Quantum Electron. 2018, 61, 98–108. [Google Scholar] [CrossRef]
- Kudryavtsev, V.N.; Chapron, B.; Myasoedov, A.G.; Collard, F.; Johannessen, J.A. On Dual Co-Polarized SAR Measurements of the Ocean Surface. IEEE Geosci. Remote Sens. Lett. 2013, 10, 761–765. [Google Scholar] [CrossRef]
- Kudryavtsev, V.; Kozlov, I.; Chapron, B.; Johannessen, J.A. Quad-polarization SAR features of ocean currents. J. Geophys. Res. Oceans 2014, 119, 6046–6065. [Google Scholar] [CrossRef] [Green Version]
- Hansen, M.W.; Kudryavtsev, V.; Chapron, B.; Brekke, C.; Johannessen, J.A. Wave Breaking in Slicks: Impacts on C-Band Quad-Polarized SAR Measurements. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4929–4940. [Google Scholar] [CrossRef] [Green Version]
- Kudryavtsev, V.N.; Fan, S.; Zhang, B.; Mouche, A.A.; Chapron, B. On Quad-Polarized SAR Measurements of the Ocean Surface. IEEE Trans. Geosci. Remote Sens. 2019, 57, 8362–8370. [Google Scholar] [CrossRef]
- Zhang, B.; Zhao, X.; Perrie, W.; Kudryavtsev, V. On Modeling of Quad-Polarization Radar Scattering from the Ocean Surface with Breaking Waves. J. Geophys. Res. Oceans 2020, 125, e2020JC016319. [Google Scholar] [CrossRef]
- Lewis, B.L.; Olin, I.D. Experimental study and theoretical model of high-resolution radar backscatter from the sea. Radio Sci. 1980, 15, 815–828. [Google Scholar] [CrossRef]
- Jessup, A.T.; Keller, W.C.; Melville, W.K. Measurements of sea spikes in microwave backscatter at moderate incidence. J. Geophys. Res. Oceans 1990, 95, 9679–9688. [Google Scholar] [CrossRef]
- Jessup, A.T.; Melville, W.K.; Keller, W.C. Breaking waves affecting microwave backscatter 1. Detection and verification. J. Geophys. Res. Oceans 1991, 96, 20547–20559. [Google Scholar] [CrossRef]
- Jessup, A.T.; Melville, W.K.; Keller, W.C. Breaking waves affecting microwave backscatter 2. Dependence on wind and wave conditions. J. Geophys. Res. Oceans 1991, 96, 20561–20569. [Google Scholar] [CrossRef]
- Lee, P.H.Y.; Barter, J.D.; Beach, K.L.; Hindman, C.L.; Lake, B.M.; Rungaldier, H.; Shelton, J.C.; Williams, A.B.; Yee, R.; Yuen, H.C. X band microwave backscattering from ocean waves. J. Geophys. Res. 1995, 100, 2591–2612. [Google Scholar] [CrossRef]
- Liu, Y.; Frasier, S.J.; McIntosh, R.E. Measurement and classification of low-grazing-angle radar sea spikes. IEEE Trans. Antennas Propag. 1998, 46, 27–40. [Google Scholar] [CrossRef] [Green Version]
- Ermakov, S.A.; Kapustin, I.A.; Kudryavtsev, V.N.; Sergievskaya, I.A.; Shomina, O.V.; Chapron, B.; Yurovskiy, Y.Y. On the Doppler Frequency Shifts of Radar Signals Backscattered from the Sea Surface. Radiophys. Quantum Electron. 2014, 57, 239–250. [Google Scholar] [CrossRef]
- Ermakov, S.A.; Dobrokhotov, V.A.; Sergievskaya, I.A.; Kapustin, I.A. Suppression of Wind Ripples and Microwave Backscattering Due to Turbulence Generated by Breaking Surface Waves. Remote Sens. 2020, 12, 3618. [Google Scholar] [CrossRef]
- Kwoh, D.S.W.; Lake, B.M. A Deterministic, Coherent, and Dual-Polarized Laboratory Study of Microwave Backscattering From Water Waves, Part 1: Short Gravity Waves Without Wind. IEEE J. Oceanic Eng. 1984, 9, 291–308. [Google Scholar] [CrossRef]
- Lamont-Smith, T.; Waseda, T.; Rheem, C.K. Measurements of the Doppler spectra of breaking waves. IET Radar Sonar Navig. 2007, 1, 149–157. [Google Scholar] [CrossRef]
- Lee, P.H.Y.; Barter, J.D.; Beach, K.L.; Lake, B.M.; Rungaldier, H.; Thompson, H.R.; Yee, R. Scattering from breaking gravity waves without wind. IEEE Trans. Antennas Propag. 1998, 46, 14–26. [Google Scholar] [CrossRef]
- Fedorov, A.V.; Melville, W.K.; Rozenberg, A. An experimental and numerical study of parasitic capillary waves. Phys. Fluids 1998, 10, 1315–1323. [Google Scholar] [CrossRef] [Green Version]
- Ericson, E.A.; Lyzenga, D.R.; Walker, D.T. Radar backscattering from stationary breaking waves. J. Geophys. Res. Oceans 1999, 104, 29679–29695. [Google Scholar] [CrossRef]
- Fuchs, J.; Regas, D.; Waseda, T.; Welch, S.; Tulin, M.P. Correlation of hydrodynamic features with LGA radar backscatter from breaking waves. IEEE Trans. Geosci. Remote Sens. 1999, 37, 2442–2460. [Google Scholar] [CrossRef]
- Walker, D. Experimentally motivated model for low grazing angle radar Doppler spectra of the sea surface. IEE Proc.-Radar Sonar Navig. 2000, 147, 114–120. [Google Scholar] [CrossRef]
- Dano, E.B.; Lyzenga, D.R.; Perlin, M. Radar Backscattering from Mechanically Generated Transient Breaking Waves—Part 1: Angle of Incidence Dependence and High Resolution Surface Morphology. IEEE J. Oceanic Eng. 2001, 26, 181–200. [Google Scholar] [CrossRef]
- Dano, E.B.; Lyzenga, D.R.; Meadows, G.; Meadows, L.; van Sumeren, H.; Onstott, R. Radar Backscattering from Mechanically Generated Transient Breaking Waves—Part 2: Azimuthal and Grazing Angle Dependence. IEEE J. Oceanic Eng. 2001, 26, 201–215. [Google Scholar] [CrossRef]
- Rozenberg, A.; Ritter, M. Laboratory study of the fine structure of short surface waves due to breaking: Two-directional wave propagation. J. Geophys. Res. Oceans 2005, 110. [Google Scholar] [CrossRef]
- Ermakov, S.A.; Kapustin, I.A.; Sergievskaya, I.A. Tank study of radar backscattering from strongly nonlinear water waves. Bull. Russ. Acad. Sci. Phys. 2010, 74, 1695–1698. [Google Scholar] [CrossRef]
- Rodriguez, E. On the Optimal Design of Doppler Scatterometers. Remote Sens. 2018, 10, 1765. [Google Scholar] [CrossRef] [Green Version]
- Yurovsky, Y.Y.; Kudryavtsev, V.N.; Grodsky, S.A.; Chapron, B. Ka-Band Dual Copolarized Empirical Model for the Sea Surface Radar Cross Section. IEEE Trans. Geosci. Remote Sens. 2016, 55, 1629–1647. [Google Scholar] [CrossRef]
- Yurovsky, Y.Y.; Kudryavtsev, V.N.; Chapron, B.; Grodsky, S.A. Modulation of Ka-band Doppler Radar Signals Backscattered from the Sea Surface. IEEE Trans. Geosci. Remote Sens. 2018, 56, 2931–2948. [Google Scholar] [CrossRef] [Green Version]
- Yurovsky, Y.Y.; Kudryavtsev, V.N.; Grodsky, S.A.; Chapron, B. Low-Frequency Sea Surface Radar Doppler Echo. Remote Sens. 2018, 10, 870. [Google Scholar] [CrossRef] [Green Version]
- Yurovsky, Y.Y.; Kudryavtsev, V.N.; Grodsky, S.A.; Chapron, B. Sea Surface Ka-Band Doppler Measurements: Analysis and Model Development. Remote Sens. 2019, 11, 839. [Google Scholar] [CrossRef]
- Monahan, E.C.; Woolf, D.K. Comments on “Variations of Whitecap Coverage with Wind stress and Water Temperature. J. Phys. Oceanogr. 1989, 19, 706–709. [Google Scholar] [CrossRef] [Green Version]
- Bondur, V.G.; Sharkov, E.A. Statistical Characteristics of Foam Formations on a Disturbed Sea-surface. Okeanologiya 1982, 22, 372–379. [Google Scholar]
- Gonzalez, R.C.; Woods, R.E.; Eddins, S.L. Digital Image Processing Using MATLAB; Gatesmark Publishing: Knoxville, TN, USA, 2009. [Google Scholar]
- Yurovsky, Y.Y.; Kudryavtsev, V.N.; Chapron, B.; Grodsky, S.A. How Fast are Fast Scatterers Associated with Breaking Wind Waves? In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 142–145. [Google Scholar] [CrossRef]
- Phillips, O.M. Radar returns from the sea surface—Bragg scattering and breaking waves. J. Phys. Oceanogr. 1988, 18, 1065–1074. [Google Scholar] [CrossRef]
- Korinenko, A.E.; Malinovsky, V.V.; Kudryavtsev, V.N. Experimental Research of Statistical Characteristics of Wind Wave Breaking. Phys. Oceanogr. 2018, 25, 489–500. [Google Scholar] [CrossRef] [Green Version]
- Hwang, P.A.; Sletten, M.A.; Toporkov, J.V. Analysis of radar sea return for breaking wave investigation. J. Geophys. Res. Oceans 2008, 113. [Google Scholar] [CrossRef]









Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yurovsky, Y.Y.; Kudryavtsev, V.N.; Grodsky, S.A.; Chapron, B. Ka-Band Radar Cross-Section of Breaking Wind Waves. Remote Sens. 2021, 13, 1929. https://doi.org/10.3390/rs13101929
Yurovsky YY, Kudryavtsev VN, Grodsky SA, Chapron B. Ka-Band Radar Cross-Section of Breaking Wind Waves. Remote Sensing. 2021; 13(10):1929. https://doi.org/10.3390/rs13101929
Chicago/Turabian StyleYurovsky, Yury Yu., Vladimir N. Kudryavtsev, Semyon A. Grodsky, and Bertrand Chapron. 2021. "Ka-Band Radar Cross-Section of Breaking Wind Waves" Remote Sensing 13, no. 10: 1929. https://doi.org/10.3390/rs13101929
APA StyleYurovsky, Y. Y., Kudryavtsev, V. N., Grodsky, S. A., & Chapron, B. (2021). Ka-Band Radar Cross-Section of Breaking Wind Waves. Remote Sensing, 13(10), 1929. https://doi.org/10.3390/rs13101929