A Deep Learning Model Using Satellite Ocean Color and Hydrodynamic Model to Estimate Chlorophyll-a Concentration
Abstract
:1. Introduction
2. Material and Methods
2.1. Study Area
2.2. Satellite Ocean Color
2.3. Hydrodynamic Model
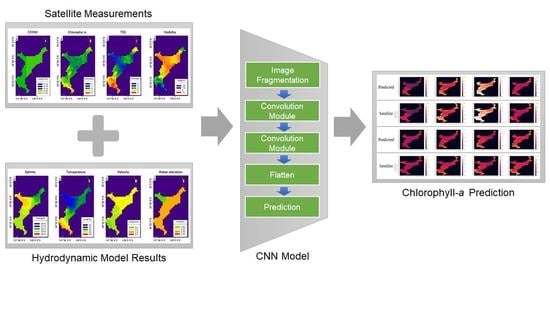
2.4. Data Structure for Deep Learning Model
2.5. Deep Learning Model Structure
3. Results
3.1. CNN Model I
3.2. CNN Model II
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Beck, M.B. Water quality modeling: A review of the analysis of uncertainty. Water Resour. Res. 1987, 23, 1393–1442. [Google Scholar] [CrossRef] [Green Version]
- Zheng, L.; Chen, C.; Zhang, F.Y. Development of water quality model in the Satilla River Estuary, Georgia. Ecol. Model. 2004, 178, 457–482. [Google Scholar] [CrossRef]
- Jia, H.; Xu, T.; Liang, S.; Zhao, P.; Xu, C. Bayesian framework of parameter sensitivity, uncertainty, and identifiability analysis in complex water quality models. Envrion. Model. Softw. 2018, 104, 13–26. [Google Scholar] [CrossRef]
- Yan, J.; Xu, Z.; Yu, Y.; Xu, H.; Gao, K. Application of a hybrid optimized BP network model to estimate water quality parameters of Beihai Lake in Beijing. Appl. Sci. 2019, 9, 1863. [Google Scholar] [CrossRef] [Green Version]
- Vargas, M.R.; de Lima, B.S.L.P.; Evsukoff, A.G. Deep learning for stock market prediction from financial news articles. In Proceedings of the 2017 IEEE International Conference on Computational Intelligence and Virtual Environments for Measurement Systems and Applications (CIVEMSA), Annecy, France, 26–28 June 2017. [Google Scholar] [CrossRef]
- Razzak, M.I.; Naz, S.; Zaib, A. Deep learning for medical image processing: Overview, challenges and the future. In Classification in BioApps; Dey, N., Ashour, A., Borra, S., Eds.; Springer: Cham, Switzerland, 2018. [Google Scholar] [CrossRef]
- Matsuoka, D.; Watanabe, S.; Sato, K.; Kawazoe, S.; Yu, W.; Easterbrook, S. Application of deep learning to estimate atmospheric gravity wave parameters in reanalysis data sets. Geophys. Res. Lett. 2020, 47, e2020GL089436. [Google Scholar] [CrossRef]
- Singh, R.; Agarwal, A.; Anthony, B.W. Mapping the design space of photonic topological states via deep learning. Opt. Express 2020, 28, 27893. [Google Scholar] [CrossRef] [PubMed]
- Xiao, C.; Chen, N.; Hu, C.; Wang, K.; Xu, Z.; Cai, Y.; Xu, L.; Chen, Z.; Gong, J. A spatiotemporal deep learning model for sea surface temperature field prediction using time-series satellite data. Envrion. Model. Softw. 2019, 120, 104502. [Google Scholar] [CrossRef]
- Guo, Y.; Cao, X.; Liu, B.; Peng, K. El Niño index prediction using deep learning with ensemble empirical mode decomposition. Symmetry 2020, 12, 893. [Google Scholar] [CrossRef]
- Shin, Y.; Kim, T.; Hong, S.; Lee, S.; Lee, E.; Hong, S.; Lee, C.; Kim, T.; Park, M.; Park, J.; et al. Prediction of chlorophyll-a concentrations in the Nakdong River using machine learning methods. Water 2020, 12, 1822. [Google Scholar] [CrossRef]
- Park, S.; Kim, J. Red tide algae image classification using deep learning based open source. Smart MediaJ. 2018, 7, 34–39. [Google Scholar]
- Lumini, A.; Nanni, L.; Maguolo, G. Deep learning for plankton and coral classification. Appl. Comput. Inform. 2019. [Google Scholar] [CrossRef]
- Raphael, A.; Dubinsky, Z.; Iluz, D.; Benichou, J.I.C.; Netanyahu, N.S. Deep neural network recognition of shallow water corals in the Gulf of Eilat(Aqaba). Sci. Rep. 2020. [Google Scholar] [CrossRef] [PubMed]
- Velasco-Gallego, C.; Lazakis, I. Real-time data-driven missing data imputation for short-time sensor data of marine systems: A comparative study. Ocean Eng. 2020, 218, 108261. [Google Scholar] [CrossRef]
- ICCG. Current Ocean-Colour Sensors. Available online: https://ioccg.org/resources/missions-instruments/current-ocean-colour-sensors/ (accessed on 16 April 2021).
- McKinna, L.I.W. Three decades of ocean-color remote-sensing Trichodesmium spp. In the World’s oceans: A review. Prog. Oceanogr. 2015, 131, 177–199. [Google Scholar] [CrossRef]
- Hu, S.B.; Cao, W.X.; Wang, G.F.; Xu, Z.T.; Lin, J.F.; Zhao, W.J.; Yang, Y.Z.; Zhou, W.; Sun, Z.H.; Yao, L.J. Comparison of MERIS, MODIS, SeaWiFS-derived particulate organic carbon, and in situ measurements in the South China Sea. Int. J. Remote Sens. 2016, 37, 1585–1600. [Google Scholar] [CrossRef]
- Werdell, P.J.; McKinna, L.I.W.; Boss, E.; Ackleson, S.G.; Craig, S.E.; Gregg, W.W.; Lee, Z.; Maritorena, S.; Roesler, C.S.; Rousseaus, C.S.; et al. An overview of approaches and challenges for retrieving marine inherent optical properties from ocean color remote sensing. Prog. Oceanogr. 2018, 160, 186–212. [Google Scholar] [CrossRef] [PubMed]
- Scott, J.P.; Werdell, P.J. Comparing level-2 and level-3 satellite ocean color retrieval validation methodologies. Opt. Express 2019, 27, 30140–30157. [Google Scholar] [CrossRef]
- Niroumand-Jadidi, M.; Bovolo, F.; Bruzzone, L. Novel spectra-derived features for empirical retrieval of water quality parameters: Demonstrations for OLI, MSI, and OLCI sensors. IEEE Trans. Geosci. Remote Sens. 2019, 57, 10285–10300. [Google Scholar] [CrossRef]
- Crout, R.L.; Ladner, S.; Lawson, A.; Martinolich, P.; Bowers, J. Calibration and validation of multiple ocean color sensors. In Proceedings of the OCEANS 2018 MTS/IEEE Conference, Charleston, SC, USA, 22–25 October 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Wang, M.; Ahn, J.H.; Jiang, L.; Shi, W.; Son, S.H.; Park, Y.J.; Ryu, J.H. Ocean color products from the Korean Geostationary Ocean Color Imager (GOCI). Opt. Express 2013, 21, 3835–3849. [Google Scholar] [CrossRef]
- Hieronymi, M.; Muller, D.; Doerffer, R. The OLCI neural network swarm(ONNS): A Bio-Geo-Optical algorithm for open ocean and costal waters. Front. Mar. Sci. 2017, 4, 140. [Google Scholar] [CrossRef] [Green Version]
- Brockmann, C.; Doerffer, R.; Peters, M.; Stelzer, K.; Embacher, S.; Ruescas, A. Evolution of the C2RCC neural network for SENTINEL 1 and 3 for the retrieval of ocean colour products in normal and extreme optically complex waters. In Proceedings of the Living Planet Symposium 2016, Prague, Czech Republic, 9–13 May 2016. [Google Scholar]
- Xie, F.; Tao, Z.; Zhou, X.; Lv, T.; Wang, J.; Li, R. A prediction model of water in situ data change under the influence of environment variables in remote sensing validation. Remote Sens. 2021, 13, 70. [Google Scholar] [CrossRef]
- Cui, A.; Xu, Q.; Gibson, K.; Liu, S.; Chen, N. Metabarcoding analysis of harmful algal bloom species in the Changjiang Estuary, China. Sci. Total Environ. 2021, 782, 146823. [Google Scholar] [CrossRef]
- Breitburg, D. Effects of hypoxia, and the balance between hypoxia and enrichment, on coastal fishes and fisheries. Estuaries 2002, 26, 767–781. [Google Scholar] [CrossRef]
- Zhao, N.; Zhang, G.; Zhang, S.; Bai, Y.; Ali, S.; Zhang, J. Temporal-Spatial Distribution of Chlorophyll-a and Impacts of Environmental Factors in the Bohai Sea and Yellow Sea. IEEE Access 2019, 7, 160947–160960. [Google Scholar] [CrossRef]
- Williams, J.J.; Esteves, L.S. Guidance on setup, calibration, and validation of hydrodynamic, wave, and sediment models for shelf seas and estuaries. Adv. Civ. Eng. 2017, 2017, 5251902. [Google Scholar] [CrossRef]
- Lee, G.; Hwang, H.J.; Kim, J.B.; Hwang, D.W. Pollution status of surface sediment in Jinju bay, a spraying shellfish farming area, Korea. J. Korean Soc. Mar. Env. Saf. 2020, 26, 392–402. [Google Scholar] [CrossRef]
- Groom, S.; Sathyendranath, S.; Ban, Y.; Bernard, S.; Brewin, R.; Brotas, V.; Brockmann, C.; Chauhan, P.; Choi, J.; Chuprin, A.; et al. Satellite ocean colour: Current status and future perspective. Front. Mar. Sci. 2019, 6, 485. [Google Scholar] [CrossRef] [Green Version]
- Minnett, P.J.; Alvera-Azcárate, A.; Chin, T.M.; Corlett, G.K.; Gentemann, C.L.; Karagali, I.; Li, X.; Marsouin, A.; Marullo, S.; Maturi, E.; et al. Half a century of satellite remote sensing of sea-surface temperature. Remote Sens. Environ. 2019, 233, 111366. [Google Scholar] [CrossRef]
- Kim, D.K.; Yoo, H.H. Analysis of temporal and spatial red tide change in the south sea of Korea using the GOCI Images of COMS. J. Korean Assoc. Geogr. Inf. Stud. 2014, 22, 129–136. [Google Scholar]
- KIOST. Korea Ocean Satellite Center. Available online: https://www.kiost.ac.kr/eng.do (accessed on 30 November 2020).
- Choi, J.K.; Park, Y.J.; Ahn, J.H.; Lim, H.S.; Eom, J.; Ryu, J.H. GOCI, the world’s first geostationary ocean color observation satellite, for the monitoring of temporal variability in coastal water turbidity. J. Geophys. Res. 2012, 117, C09004. [Google Scholar] [CrossRef]
- Lee, K.H.; Lee, S.H. Monitoring of floating green algae using ocean color satellite remote sensing. J. Korean Assoc. Geogr. Inf. Stud. 2012, 15, 137–147. [Google Scholar] [CrossRef]
- Huang, C.; Yang, H.; Zhu, A.; Zhang, M.; Lu, H.; Huan, T.; Zou, J.; Li, Y. Evaluation of the geostationary ocean color imager (GOCI) to monitor the dynamic characteristics of suspension sediment in Taihu Lake. Int. J. Remote Sens. 2015, 36, 3859–3874. [Google Scholar] [CrossRef]
- Concha, J.; Mannino, A.; Franz, B.; Bailey, S.; Kim, T. Vicarious calibration of GOCI for the SeaDAS ocean color retrieval. Int. J. Remote Sens. 2019, 40, 3984–4001. [Google Scholar] [CrossRef]
- Ryu, J.H.; Han, H.J.; Cho, S.; Park, Y.J.; Ahn, Y.H. Overview of geostationary ocean color imager(GOCI) and GOCI Data Processing System(GDPS). Ocean Sci. J. 2012, 47, 223–233. [Google Scholar] [CrossRef]
- Lesser, G.R.; Roelvink, J.A.; van Kester, J.A.T.M.; Stelling, G.S. Development and validation of a three-dimensional morphological model. Coast. Eng. 2004, 51, 883–915. [Google Scholar] [CrossRef]
- Hu, K.; Ding, P.; Wang, Z.; Yang, S. A 2D/3D hydrodynamic and sediment transport model for the Yangtze estuary, China. J. Mar. Syst. 2009, 77, 114–136. [Google Scholar] [CrossRef]
- Dissanayake, P.; Hofmann, H.; Peeters, F. Comparison of results from two 3D hydrodynamic models with field data: Internal seiches and horizontal currents. Inland Waters 2019, 9, 239–260. [Google Scholar] [CrossRef]
- Ramos, V.; Carballo, R.; Ringwood, J.V. Application of the actuator disc theory of Delft3D-FLOW to model far-field hydrodynamic impacts of tidal turbines. Renew. Energy 2019, 139, 1320–1335. [Google Scholar] [CrossRef]
- Xia, M.; Jiang, L. Application of an unstructured grid-based water quality model to Chaeapeake Bay and its adjacent coastal ocean. J. Mar. Sci. Eng. 2016, 4, 52. [Google Scholar] [CrossRef] [Green Version]
- Hartnett, M.; Nash, S. An integrated measurement and modelling methodoloby for estuarine water quality management. Water Sci. Eng. 2015, 8, 9–19. [Google Scholar] [CrossRef] [Green Version]
- Kim, W.K.; Moon, J.E.; Park, Y.J.; Ishizaka, J. Evaluation of chlorophyll retrievals form Geostationary Ocean Imager(GOCI) for the North-East Asian region. Remote Sens. Environ. 2016, 184, 482–495. [Google Scholar] [CrossRef]


















| Category | Training Data | Validation Data | Test Data |
|---|---|---|---|
| Period (year) | 2015–2017 | 2018 | 2019 |
| CNN Model I (# of images) | 932 | 271 | 128 |
| CNN Model II (# of segmented images (7 × 7)) | 293,580 | 85,365 | 40,320 |
| Input Variables | RMSE |
|---|---|
| CDOM | 0.231 |
| TSS | 0.526 |
| Visibility | 0.492 |
| Currents | 0.651 |
| Salinity | 0.648 |
| Temperature | 0.545 |
| Water level | 0.653 |
| All except CDOM | 0.330 |
| All | 0.191 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, D.; Lee, E.; Kwon, K.; Kim, T. A Deep Learning Model Using Satellite Ocean Color and Hydrodynamic Model to Estimate Chlorophyll-a Concentration. Remote Sens. 2021, 13, 2003. https://doi.org/10.3390/rs13102003
Jin D, Lee E, Kwon K, Kim T. A Deep Learning Model Using Satellite Ocean Color and Hydrodynamic Model to Estimate Chlorophyll-a Concentration. Remote Sensing. 2021; 13(10):2003. https://doi.org/10.3390/rs13102003
Chicago/Turabian StyleJin, Daeyong, Eojin Lee, Kyonghwan Kwon, and Taeyun Kim. 2021. "A Deep Learning Model Using Satellite Ocean Color and Hydrodynamic Model to Estimate Chlorophyll-a Concentration" Remote Sensing 13, no. 10: 2003. https://doi.org/10.3390/rs13102003
APA StyleJin, D., Lee, E., Kwon, K., & Kim, T. (2021). A Deep Learning Model Using Satellite Ocean Color and Hydrodynamic Model to Estimate Chlorophyll-a Concentration. Remote Sensing, 13(10), 2003. https://doi.org/10.3390/rs13102003