Spherically Optimized RANSAC Aided by an IMU for Fisheye Image Matching
Abstract
:1. Introduction
2. Related Work
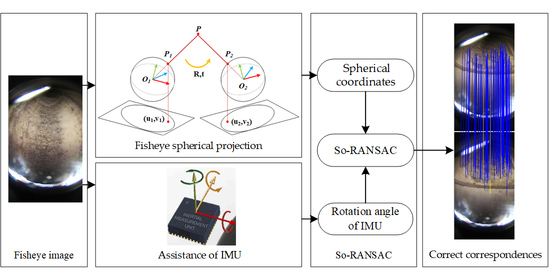
3. Spherically Optimized RANSAC Aided by an IMU
3.1. Camera Model and Feature Matching
3.2. Fisheye Image Matching Aided by an IMU
3.2.1. Fisheye Spherical Projection
3.2.2. Relative Rotation Angle
3.2.3. RANSAC Aided by the IMU
| Algorithm 1. So-RANSAC aided by IMU |
| Input: putative set M, relative rotation angle θ, fisheye camera calibration parameters |
| Initialization: |
| 1. The putative set M is projected onto the sphere, and the spherical set S is obtained |
| 2. for i=1:N do |
| 3. Select a minimum sample set (4 correspondences) from S |
| 4. The essential matrix E is estimated, and the attitude of the model is given by θ |
| 5. The reprojection error of S is calculated according to model E, and the number of inner points Ninliers is calculated. |
| 6. The model with the largest Ninliers is regarded as the best model |
| 7. end for |
| 8. Save the optimal model Eoptimal and the inliers |
| Output: Inliers |
4. Results
4.1. Experimental Data
4.2. Image Matching Results
4.3. Reprojection Error
4.4. Computation Time
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Zhang, Z.; Rebecq, H.; Forster, C.; Scaramuzza, D. Benefit of Large Field-of-View Cameras for Visual Odometry. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 801–808. [Google Scholar] [CrossRef] [Green Version]
- Hughes, C.; Glavin, M.; Jones, E.; Denny, P. Wide-Angle Camera Technology for Automotive Applications: A Review. IET Intell. Transp. Syst. 2009, 3, 19. [Google Scholar] [CrossRef] [Green Version]
- Liu, Z. State of the Art Review of Inspection Technologies for Condition Assessment of Water Pipes. Measurement 2013, 46, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Hartley, R.; Mashford, J.; Wang, L. Pipeline Reconstruction from Fisheye Images. J. WSCG 9 2011, 19, 49–57. [Google Scholar]
- Nister, D. An Efficient Solution to the Five-Point Relative Pose Problem. IEEE Trans. Pattern Anal. Mach. Intell. 2004, 26, 756–770. [Google Scholar] [CrossRef] [PubMed]
- Ma, J.; Jiang, X.; Fan, A.; Jiang, J.; Yan, J. Image Matching from Handcrafted to Deep Features: A Survey. Int. J. Comput. Vis. 2021, 129, 23–79. [Google Scholar] [CrossRef]
- Scaramuzza, D.; Martinelli, A.; Siegwart, R. A Flexible Technique for Accurate Omnidirectional Camera Calibration and Structure from Motion. In Proceedings of the Fourth IEEE International Conference on Computer Vision Systems (ICVS’06), New York, NY, USA, 4–7 January 2006; p. 45. [Google Scholar] [CrossRef] [Green Version]
- Kannala, J.; Brandt, S.S. A Generic Camera Model and Calibration Method for Conventional, Wide-Angle, and Fish-Eye Lenses. IEEE Trans. Pattern Anal. Mach. Intell. 2006, 28, 1335–1340. [Google Scholar] [CrossRef] [Green Version]
- Puig, L.; Bermúdez, J.; Sturm, P.; Guerrero, J.J. Calibration of Omnidirectional Cameras in Practice: A Comparison of Methods. Comput. Vis. Image Underst. 2012, 116, 120–137. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Zhao, P.; Hu, Q.; Ai, M.; Hu, D.; Li, J. A UAV-Based Panoramic Oblique Photogrammetry (POP) Approach Using Spherical Projection. ISPRS J. Photogramm. Remote Sens. 2020, 159, 198–219. [Google Scholar] [CrossRef]
- Zhao, Q.; Wan, L.; Feng, W.; Zhang, J.; Wong, T.-T. Cube2Video: Navigate Between Cubic Panoramas in Real-Time. IEEE Trans. Multimed. 2013, 15, 1745–1754. [Google Scholar] [CrossRef]
- Ha, S.J.; Koo, H.I.; Lee, S.H.; Cho, N.I.; Kim, S.K. Panorama Mosaic Optimization for Mobile Camera Systems. IEEE Trans. Consum. Electron. 2007, 53, 9. [Google Scholar] [CrossRef] [Green Version]
- Coorg, S.; Teller, S. Spherical Mosaics with Quaternions and Dense Correlation. Int. J. Comput. Vis. 2000, 37, 259–273. [Google Scholar] [CrossRef]
- Lowe, D.G. Distinctive Image Features from Scale-Invariant Keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Rublee, E.; Rabaud, V.; Konolige, K.; Bradski, G. ORB: An Efficient Alternative to SIFT or SURF. In Proceedings of the 2011 International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; IEEE: Barcelona, Spain, 2011; pp. 2564–2571. [Google Scholar] [CrossRef]
- Furnari, A.; Farinella, G.M.; Bruna, A.R.; Battiato, S. Distortion Adaptive Sobel Filters for the Gradient Estimation of Wide Angle Images. J. Vis. Commun. Image Represent. 2017, 46, 165–175. [Google Scholar] [CrossRef]
- Puig, L.; Guerrero, J.J.; Daniilidis, K. Scale Space for Camera Invariant Features. IEEE Trans. Pattern Anal. Mach. Intell. 2014, 36, 1832–1846. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mikolajczyk, K.; Tuytelaars, T.; Schmid, C.; Zisserman, A.; Matas, J.; Schaffalitzky, F.; Kadir, T.; Gool, L.V. A Comparison of Affine Region Detectors. Int. J. Comput. Vis. 2005, 65, 43–72. [Google Scholar] [CrossRef] [Green Version]
- Furnari, A.; Farinella, G.M.; Bruna, A.R.; Battiato, S. Affine Covariant Features for Fisheye Distortion Local Modeling. IEEE Trans. Image Process. 2017, 26, 696–710. [Google Scholar] [CrossRef]
- Arican, Z.; Frossard, P. Scale-Invariant Features and Polar Descriptors in Omnidirectional Imaging. IEEE Trans. Image Process. 2012, 21, 2412–2423. [Google Scholar] [CrossRef] [Green Version]
- Cruz-Mota, J.; Bogdanova, I.; Paquier, B.; Bierlaire, M.; Thiran, J.-P. Scale Invariant Feature Transform on the Sphere: Theory and Applications. Int. J. Comput. Vis. 2012, 98, 217–241. [Google Scholar] [CrossRef]
- Lourenco, M.; Barreto, J.P.; Vasconcelos, F. SRD-SIFT: Keypoint Detection and Matching in Images with Radial Distortion. IEEE Trans. Robot. 2012, 28, 752–760. [Google Scholar] [CrossRef]
- Fitzgibbon, A.W. Simultaneous Linear Estimation of Multiple View Geometry and Lens Distortion. In Proceedings of the 2001 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, CVPR 2001, Kauai, HI, USA, 8–14 December 2001; pp. I-125–I-132. [Google Scholar] [CrossRef]
- Ma, J.; Zhao, J.; Tian, J.; Yuille, A.L.; Tu, Z. Robust Point Matching via Vector Field Consensus. IEEE Trans. Image Process. 2014, 23, 1706–1721. [Google Scholar] [CrossRef] [Green Version]
- Ma, J.; Zhao, J.; Jiang, J.; Zhou, H.; Guo, X. Locality Preserving Matching. Int. J. Comput. Vis. 2019, 127, 512–531. [Google Scholar] [CrossRef]
- Li, J.; Hu, Q.; Ai, M. LAM: Locality Affine-Invariant Feature Matching. ISPRS J. Photogramm. Remote Sens. 2019, 154, 28–40. [Google Scholar] [CrossRef]
- Li, J.; Hu, Q.; Ai, M. 4FP-Structure: A Robust Local Region Feature Descriptor. Photogramm. Eng. Remote Sens. 2017, 83, 813–826. [Google Scholar] [CrossRef]
- Campos, M.B.; Tommaselli, A.M.G.; Castanheiro, L.F.; Oliveira, R.A.; Honkavaara, E. A Fisheye Image Matching Method Boosted by Recursive Search Space for Close Range Photogrammetry. Remote Sens. 2019, 11, 1404. [Google Scholar] [CrossRef] [Green Version]
- Scaramuzza, D.; Fraundorfer, F.; Siegwart, R. Real-Time Monocular Visual Odometry for on-Road Vehicles with 1-Point RANSAC. In Proceedings of the 2009 IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; pp. 4293–4299. [Google Scholar] [CrossRef]
- Li, B.; Heng, L.; Lee, G.H.; Pollefeys, M. A 4-Point Algorithm for Relative Pose Estimation of a Calibrated Camera with a Known Relative Rotation Angle. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013; pp. 1595–1601. [Google Scholar] [CrossRef]
- Valiente, D.; Gil, A.; Reinoso, Ó.; Juliá, M.; Holloway, M. Improved Omnidirectional Odometry for a View-Based Mapping Approach. Sensors 2017, 17, 325. [Google Scholar] [CrossRef] [Green Version]
- Yi, K.M.; Trulls, E.; Ono, Y.; Lepetit, V.; Salzmann, M.; Fua, P. Learning to find good correspondences. arXiv 2018, arXiv:1711.05971. [Google Scholar]
- Pourian, N.; Nestares, O. An End to End Framework to High Performance Geometry-Aware Multi-Scale Keypoint Detection and Matching in Fisheye Imag. In Proceedings of the 2019 IEEE International Conference on Image Processing (ICIP), Taipei, Taiwan, 22–25 September 2019; pp. 1302–1306. [Google Scholar] [CrossRef]
- Liu, S.; Guo, P.; Feng, L.; Yang, A. Accurate and Robust Monocular SLAM with Omnidirectional Cameras. Sensors 2019, 19, 4494. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, H.H. A Screw Motion Approach to Uniqueness Analysis of Head-Eye Geometry. In Proceedings of the 1991 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Maui, HI, USA, 3–6 June 1991; pp. 145–151. [Google Scholar] [CrossRef]
- Madgwick, S.O.H.; Harrison, A.J.L.; Vaidyanathan, R. Estimation of IMU and MARG Orientation Using a Gradient Descent Algorithm. In Proceedings of the 2011 IEEE International Conference on Rehabilitation Robotics, Zurich, Switzerland, 29 June–1 July 2011; pp. 1–7. [Google Scholar] [CrossRef]
- Hartley, R.; Zisserman, A. Multiple View Geometry in Computer Vision; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Iachello, F. Lie Algebras and Applications; Lecture Notes in Physics; Springer: Berlin/Heidelberg, Germany, 2015; Volume 891. [Google Scholar] [CrossRef] [Green Version]
- Matsuki, H.; von Stumberg, L.; Usenko, V.; Stuckler, J.; Cremers, D. Omnidirectional DSO: Direct Sparse Odometry With Fisheye Cameras. IEEE Robot. Autom. Lett. 2018, 3, 3693–3700. [Google Scholar] [CrossRef] [Green Version]










| Main Components of the Robot | Parameters |
|---|---|
| CMOS | IMX274 1080p HD sensor |
| Lens | 220° wide-angle HD lens |
| Video resolution | HD 1080p |
| Frame rate | 1080p 60 fps |
| IMU | ICM-20689 high-performance 6-axis MEMS |
| Scheme 1 | Information |
|---|---|
| Parameters | (1) So-RANSAC, Four-point RANSAC, RANSAC: p = 0.99, T = 3 (2) LPM, VFC: default |
| Data sets | (1) TUM data set: sequence_01, 50 images; sequence_05, 50 images; sequence_14, 50 images (2) Pipeline data set 1: 50 images; Pipeline data set 2: 50 images |
| Methods | (1) RANSAC, C++, OpenCV 2.4.9 (2) Four-point RANSAC, C++: https://github.com/prclibo/relative-pose-estimation/tree/master/four-point-groebner (3) LPM, MATLAB: https://github.com/jiayi-ma/LPM (4) VFC, MATLAB: https://github.com/jiayi-ma/VFC |
| Evaluation metrics | Precision; recall; F-score; MAE; RMSE |
| Method | Correct Matches Number | Success Rate/% |
|---|---|---|
| RANSAC | 127.15 | 96 |
| LPM | 190.45 | 100 |
| Four-Point RANSAC | 147.21 | 96 |
| VFC | 187.19 | 100 |
| So-RANSAC | 165.27 | 96 |
| Method | Precision | Recall | F-Score |
|---|---|---|---|
| RANSAC | 0.832693 | 0.757375 | 0.793250 |
| LPM | 0.664963 | 0.968233 | 0.788440 |
| Four-Points RANSAC | 0.888411 | 0.824689 | 0.855364 |
| VFC | 0.655793 | 0.957326 | 0.778377 |
| So-RANSAC | 0.925717 | 0.884100 | 0.904430 |
| Method | MAE/Pixels | RMSE/Pixels |
|---|---|---|
| RANSAC | 2.757730 | 3.119673 |
| Four-Points RANSAC | 2.208425 | 3.093145 |
| So-RANSAC | 1.595407 | 2.109953 |
| Method | Times/s |
|---|---|
| LPM | 0.013 |
| VFC | 0.226 |
| RANSAC | 0.373 |
| Four-Points RANSAC | 0.651 |
| So-RANSAC | 0.719 |
| Method | Correct Matches Number | Success Rate/% | Precision |
|---|---|---|---|
| MARG | 165.27 | 96 | 0.925717 |
| Kalman | 165.13 | 96 | 0.924592 |
| Simulation | 152.55 | 96 | 0.854469 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, A.; Li, Q.; Chen, Z.; Zhang, D.; Zhu, J.; Yu, J.; Fang, X. Spherically Optimized RANSAC Aided by an IMU for Fisheye Image Matching. Remote Sens. 2021, 13, 2017. https://doi.org/10.3390/rs13102017
Liang A, Li Q, Chen Z, Zhang D, Zhu J, Yu J, Fang X. Spherically Optimized RANSAC Aided by an IMU for Fisheye Image Matching. Remote Sensing. 2021; 13(10):2017. https://doi.org/10.3390/rs13102017
Chicago/Turabian StyleLiang, Anbang, Qingquan Li, Zhipeng Chen, Dejin Zhang, Jiasong Zhu, Jianwei Yu, and Xu Fang. 2021. "Spherically Optimized RANSAC Aided by an IMU for Fisheye Image Matching" Remote Sensing 13, no. 10: 2017. https://doi.org/10.3390/rs13102017
APA StyleLiang, A., Li, Q., Chen, Z., Zhang, D., Zhu, J., Yu, J., & Fang, X. (2021). Spherically Optimized RANSAC Aided by an IMU for Fisheye Image Matching. Remote Sensing, 13(10), 2017. https://doi.org/10.3390/rs13102017