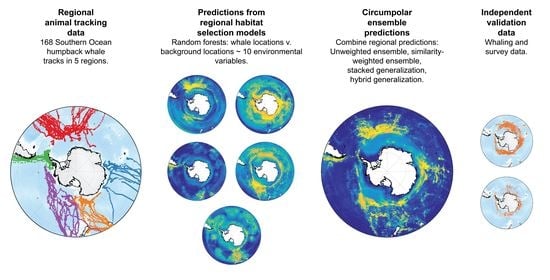
Combining Regional Habitat Selection Models for Large-Scale Prediction: Circumpolar Habitat Selection of Southern Ocean Humpback Whales

Abstract

Machine learning algorithms are often used to model and predict animal habitat selection—the relationships between animal occurrences and habitat characteristics. For broadly distributed species, habitat selection often varies among populations and regions; thus, it would seem preferable to fit region- or population-specific models of habitat selection for more accurate inference and prediction, rather than fitting large-scale models using pooled data. However, where the aim is to make range-wide predictions, including areas for which there are no existing data or models of habitat selection, how can regional models best be combined? We propose that ensemble approaches commonly used to combine different algorithms for a single region can be reframed, treating regional habitat selection models as the candidate models. By doing so, we can incorporate regional variation when fitting predictive models of animal habitat selection across large ranges. We test this approach using satellite telemetry data from 168 humpback whales across five geographic regions in the Southern Ocean. Using random forests, we fitted a large-scale model relating humpback whale locations, versus background locations, to 10 environmental covariates, and made a circumpolar prediction of humpback whale habitat selection. We also fitted five regional models, the predictions of which we used as input features for four ensemble approaches: an unweighted ensemble, an ensemble weighted by environmental similarity in each cell, stacked generalization, and a hybrid approach wherein the environmental covariates and regional predictions were used as input features in a new model. We tested the predictive performance of these approaches on an independent validation dataset of humpback whale sightings and whaling catches. These multiregional ensemble approaches resulted in models with higher predictive performance than the circumpolar naive model. These approaches can be used to incorporate regional variation in animal habitat selection when fitting range-wide predictive models using machine learning algorithms. This can yield more accurate predictions across regions or populations of animals that may show variation in habitat selection.

1. Introduction

Modelling the habitat selection of animals—that is, estimating functions of their disproportionate use of habitats characterized by a set of covariates—is a frequent task in animal ecology, to address both fundamental and applied questions [1,2]. In common with the broader set of methods called species distribution models, many habitat selection models are correlative models that relate the occurrence of animals to environmental covariates, and the application of various machine learning (or statistical learning) algorithms to achieve this has become commonplace (e.g., [3,4,5,6]). These algorithms “learn” predictive functions relating outputs (animal occurrence) to a set of inputs (habitat/environmental covariates), and their flexibility and high predictive power is advantageous in modelling and mapping the complex relationships between animal occurrences and habitat characteristics (e.g., [7]).

In broadly distributed animal species, habitat selection often varies among populations or regions (e.g., [8,9,10,11]) due to causes including functional responses in habitat selection (a change in the selection of a habitat type depending on its availability) [12,13], density-dependent habitat selection (where competition causes animals to use less favorable habitats) (e.g., [14,15]), and intraspecific niche variation (e.g., [16]). For example, two habitat selection models fitted using satellite tracking data for grey petrels (Procellaria cinerea) from two Southern Ocean archipelagos performed poorly when predicted between the two archipelagos, and also when validated with tracking data from a third archipelago [8]. In this case, the poor transferability of the two models indicated that they were not generalizable (the models did not extrapolate well across sites), even though the habitat selection of petrels from the two archipelagos was broadly similar [8].

Thus, it would seem preferable to fit region- or population-specific models of habitat selection for more accurate inference and prediction, rather than fitting large-scale or range-wide models using pooled data. This can be taken into account in mixed-effects or hierarchical models (e.g., [17]). Matthiopoulos et al. [18] proposed “generalized functional responses” to overcome the problem of habitat selection functions varying between environments, but these specific modelling approaches are not applicable to the machine learning algorithms now frequently used for modelling habitat selection (e.g., [7,19]). Prediction is often the goal when using such algorithms, and this frequently includes spatial extrapolation beyond the area where the data used in the model were obtained. Where the aim is to make large-scale predictions across regions, typically including areas for which there are no existing data or models of habitat selection, how can regional models best be combined? This is a special kind of spatial extrapolation problem: in the extrapolation region, we have several candidate models, but we do not know which of these regional models should be used to make predictions. In machine learning applications, when multiple competing models are available, the typical approach is to combine the models somehow into an “ensemble” [20,21,22,23]. The usual case is when predictions from multiple algorithms are combined into an ensemble, often using some kind of consensus (such as unweighted (e.g., [24]) or weighted (e.g., [25]) means), or by training a so-called meta-learner or meta-model, which relates the predictions of several models or algorithms to the original response data. The latter includes stacking, where the meta-model is a regression (e.g., [26]). We propose that the regional models can be treated as competing candidate models. By doing so, we can reframe ensemble approaches to incorporate regional variation in animal telemetry data when fitting predictive models of habitat selection, and we test such an approach in this paper. As well as testing unweighted ensembles and stacked generalization (a meta-model), we introduce two specific approaches for solving this problem: similarity-weighted ensembles and hybrid generalization.

This issue is especially relevant in the case of large marine vertebrates, since they are highly mobile and often widely distributed. However, large-scale predictive models are frequently used to study them (e.g., [27]), despite several studies showing regional variation in habitat selection [8,9,10,11,28]. Humpback whales (Megaptera novaeangliae) are large marine vertebrates with a cosmopolitan distribution, which migrate seasonally between foraging and breeding areas [29]. In the Southern Hemisphere, seven breeding populations (“breeding stocks” A–G) [30] from discrete low-latitude winter breeding areas in the Atlantic, Indian, and Pacific Oceans migrate to summer foraging areas in the Southern Ocean around Antarctica. Published humpback whale tracking data for the Southern Ocean [31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48] (suggest that there is region-specific habitat selection in Southern Ocean humpback whales. This case thus presents a good scenario for testing how region-specific habitat selection patterns can be included in large-scale predictions.

Here, we design and fit various habitat selection models to tracking data for Southern Hemisphere humpback whales, with the goal of generating Southern Ocean-wide predictions. We test different methods for incorporating regional differences in habitat selection into predictive models, and compare these to a naive circumpolar habitat model that is agnostic to any predefined regional information. We apply these models to predict the circumpolar habitat selection of humpback whales around the Antarctic continent, and validate the predictions with independent data on humpback whale catches and sightings. Our expectation is that models including information on regional habitat selection should have higher predictive performance than the naive model.

2. Methods

All computation was performed in the R environment [49], and scripts associated with the analyses are available at: https://github.com/ryanreisinger/megaPrediction (accessed on 21 May 2021).

2.1. Whale Tracking Data

We compiled published and unpublished satellite tracking data from 378 individual humpback whales, totaling 291,628 location records. Argos satellite-linked telemetry tags were deployed on humpback whales in their breeding areas and Antarctic foraging areas from 2002–2018 [31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48] (Supplementary Table S1). Adult individuals were selected for tagging in these study areas indiscriminately; specific individuals were not targeted. Details of tag types, ethics clearance, and permits are provided in the above references. This comprehensive dataset represents the movements of whales from seven Southern Hemisphere “breeding stocks” [30] across different ocean basins in and around the Southern Ocean.

Argos locations are recorded at irregular time intervals due to differences in the programming of telemetry tags, and because locations can be obtained only when the tag is not underwater. Furthermore, the spatial accuracy of each location may vary, as indicated by the quality class assigned to it. To estimate whale locations at regular time intervals while taking into account these different accuracies, we used the foieGras package [50,51] to fit a random walk state–space model [52,53,54,55] with a 24-h time step to the Argos tracking data. Before fitting the model, we excluded tracks with fewer than 10 locations, and we filtered the data using a speed–distance–angle filter from the argosfilter package [56], with a speed threshold of 5 m/s to exclude unlikely locations. We used a less conservative speed threshold than some other humpback whale studies (e.g., 12 m/s in Garrigue et al. [36]), based on visual inspection of the resulting track fits and our exploratory analyses, in which a higher number of state–space models failed to fit when using more conservative speed estimates. We then removed data north of 40° S and, lastly, retained only tracks with >5 location estimates. These steps resulted in a filtered set of 168 tracks, totaling 9219 regularized location estimates. We assigned the tracks to five geographic regions based on a visual assessment of the circumpolar distribution of the tracks, together with information on the putative “breeding stock” [30] of the tracked individuals (Figure 1).

2.2. Estimating Whale Habitat Availability

To estimate the habitat selection of humpback whales, we used a case–control design [17], wherein we modelled the environmental characteristics of the locations where whales were present (the utilized habitat, or cases, here represented by the observed tracks) compared to the environmental characteristics of locations that whales could potentially have used (the available habitat, or controls). In order to estimate the available habitat, for each observed track we simulated 50 tracks using a first-order vector autoregressive model [19], using the availability package [57]. These simulated tracks preserved the duration, speed, and turning angle characteristics of the corresponding observed track, indicating where a given animal could have travelled if it had no habitat preference [19,26,27]. Together, this yielded a dataset of 468,588 locations, comprising 9188 observed locations and 459,400 simulated locations.

2.3. Environmental Covariates

To characterize the habitats used by, and available to, humpback whales, we compiled a set of four static environmental covariates related to bathymetry—ocean depth (DEPTH), bottom slope (SLOPE), distance to the Antarctic upper slope (SLOPEDIST), and distance to the nearest shelf break (SHELFDIST)—and six dynamic covariates related to sea ice and sea surface temperature—sea ice concentration (ICE) and its intraseasonal variance (ICEVAR), distance to the sea ice edge (ICEDIST), sea surface temperature (SST), its gradient (SSTFRONT), and its intraseasonal variance (SSTVAR) (

Table 1. Environmental covariates. Details of the data used to calculate 10 environmental covariates used in models of humpback whale habitat selectivity.

Abbreviation Name	Unit	Notes	Spatial Resolution	Temporal Resolution	Source Link	Citation
Bathymetry
DEPTH	m	GEBCO_2019 grid.	15 arc s (0.004°)	-	https://www.gebco.net/data_and_products/gridded_bathymetry_data/gebco_2019/gebco_2019_info.html (accessed on 21 May 2021)	[58]
Ocean depth
SLOPE	°	Calculated from DEPTH using the raster::terrain function.	15 arc s (0.004°)	-	-	-
Bottom slope
SHELFDIST	km	Derived from Smith and Sandwell V13.1 and ETOPO1 bathymetry data by Raymond [59]. Points in less than 500 m of water (i.e., over the shelf) were assigned negative distances.		-	https://data.aad.gov.au/metadata/records/Polar_Environmental_Data (accessed on 21 May 2021)	[59]
Distance to nearest area of sea floor of depth 500 m or less
SLOPEDIST	km	Distance to the “upper slope” geomorphic feature, from Post (unpublished data), expanded from O’Brien et al. [60]. Mapping based on GEBCO contours, ETOPO2, and seismic lines. Points inside of an “upper slope” polygon were assigned negative distances.	0.1°	-	https://data.aad.gov.au/metadata/records/Polar_Environmental_Data (accessed on 21 May 2021)	[60]
Distance to the Antarctic upper slope						[59]
Temperature
SST	°C	NOAA Optimum Interpolation Sea Surface Temperature v 2.0, AVHRR only	0.25°	Daily	https://www.ncei.noaa.gov/data/sea-surface-temperature-optimum-interpolation/v2/access/avhrr-only/(accessed on 21 May 2021)	[61]
Mean SST
SSTVAR	°C			Daily	-	-
Mean of SST intraseasonal variance
SSTFRONT	°C/km	Calculated from SST using the grec::detectFronts function [62], which implements Belkin & O’Reilly’s [63] algorithm.	0.25°	Daily	-	-
Mean SST gradient
Sea ice
ICE	%	Sea Ice Concentrations from Nimbus-7 SMMR and DMSP SSM/I-SSMIS Passive Microwave Data, Version 1.	25 km	Daily	https://nsidc.org/data/NSIDC-0051/versions/1 (accessed on 21 May 2021)	[64]
Mean sea ice concentration
ICEVAR	%	Calculated from ICE.	25 km	Daily	-	-
Mean of sea ice concentration intraseasonal variance
ICEDIST	km	Calculated from ICE using the raster::rasterToContour function, with sea ice edge defined as the 15% sea ice concentration contour.	25 km	Daily	-	-
Distance to sea ice edge

, Figure 2). These variables are among those widely used to represent the habitat of Southern Ocean marine predators (e.g., [19,26,27]), including humpback whales [32,40,42,45], since they represent or create conditions and features associated with increased primary productivity and the elevated abundance and aggregation of prey. To facilitate the comparison and prediction of the different models in our study, for dynamic covariates we compiled a single climatology layer for each covariate across the whole study area that was circumpolar (180° E–180° W) and south of 40° S, on a 0.1° by 0.1° grid. Covariates were resampled onto this grid using bilinear interpolation. The grid spatial resolution is a compromise between the lowest (SST, SSTVAR, SSTFRONT = 0.25°) and highest (DEPTH, SLOPE = 0.004°) resolutions among the covariates.

For each dynamic covariate (ICE, ICEVAR, ICEDIST, SST, SSTVAR, and SSTFRONT), the climatology was calculated by first extracting daily rasters at weekly intervals from 1 November 1999 to 31 March 2019 (sea ice covariates) or 1 November 2002 to 31 March 2019 (sea surface temperature covariates), retaining only dates in November–March (n = 431 days) to match the timespan of the tracking data. For the mean covariates among these (ICE, ICEDIST, SST, and SSTFRONT), the temporal average of these rasters was calculated. For variance covariates among these (ICEVAR, SSTVAR), the temporal variance was calculated within each season (November–March of a given austral summer), and the mean of these variance values was then calculated. After resampling covariates onto the study area grid, we filled any remaining data gaps in the mean layers by taking the mean value from a 13 cell by 13 cell (1.3° by 1.3°) neighborhood focused on the given cell.

For model fitting, the values of these covariates were extracted at locations of the real and simulated tracks. For spatial prediction, we predicted according to covariate values across the whole study area grid (Figure 2). For these calculations we used mainly tools in the raster [65], raadtools [66], and grec [62] packages.

2.4. Modelling Approaches

To model humpback whale habitat selection, we tested five approaches: a circumpolar model (M1) that does not include regional variation explicitly, and four kinds of ensembles (M2–M5), which incorporate regional information in different ways. Hereafter, we use “regional” to refer to tracks from each of five regions defined a priori: Atlantic, East Pacific, Pacific, West Pacific, and East Indian. We use “circumpolar” to refer to the whole study area: 180° E—180° W and south of 40° S.

2.4.1. M1—A Naive Circumpolar Model

Here, we fit a case–control classification model where the response (or output) is whether a given location in the dataset is an observed track location (case) or a simulated track location (control), and the features (or inputs) are a set of environmental covariates at that location, as described above. M1 is fitted using tracking data plus simulations from all regions together, with no information on region identity, and the fitted model is predicted circumpolarly. We thus refer to this as the “naive circumpolar model”. This circumpolar prediction is the probability (0–1) in each grid cell of that grid cell containing an observed (as opposed to a simulated) track location, which we interpret as a measure of habitat selection (e.g., [19,26,27]).

2.4.2. Mr—Regional Models

As “features” (predictor variables) for models M2–M5, we first fit five regional models using the same method as for M1. Each of these regional models uses tracking data plus simulations from a single region only, but is predicted (extrapolated) circumpolarly. This set of five predictions in each circumpolar grid cell is then used as features in different ways for M2–M5.

2.4.3. M2—Unweighted Ensemble (Simple Averaging)

In this unweighted ensemble, or simple average, we do not fit a new classification model. Rather we take, in each circumpolar grid cell, an unweighted mean of the predictions from the regional models [21]. The final prediction layer thus combines information from each regional prediction, but is agnostic as to how appropriate each of the five regional predictions may be in a given circumpolar grid cell, allowing each regional prediction to have equal weight.

2.4.4. M3—Similarity-Weighted Ensemble

Here, we first fit a multiclass classifier where the response is the region identity of each tracking location (but not simulations), and the features are the environmental covariates at that location. The fitted model thus predicts, given a set of environmental covariates, the probability that a given location belongs to each of the five regions. We predict this model for the circumpolar area in order to obtain a probability that each grid cell “belongs to” a certain region. We then use these probabilities to weight the corresponding predictions from the regional models, obtaining an ensemble where the predictions in each grid cell are weighted by the similarity of that cell to the environmental conditions where the regional model was fitted. Like M2, this model combines information from each regional prediction, but unlike M2 it weights the predictions by a local measure of their “appropriateness”. We thus refer to this model as a similarity-weighted ensemble.

2.4.5. M4—Stacked Generalization

Here, we fit an additional model (the “second-level model”) where the response is whether a given location in the dataset is an observed track location or a simulated track location, and the features are predictions from the five regional models (the “first-level models”). No environmental covariates are included among the features. We then predict this model circumpolarly. This kind of model is referred to as a “stacked generalization” [67], “meta-learner”, or “meta-model” [68], and is a widely used method for creating ensembles of models that attempt to account for different model performance [21], overall and/or locally.

2.4.6. M5—Hybrid Generalization

Finally, we fit a new model where the response is whether a given location in the dataset is an observed track location or a simulated track location, and the features are environmental covariates plus predictions from the five regional models. The model is thus additionally “informed” by the predictions from the regional models, and we term this “hybrid generalization” to reflect that it combines approaches from the M1 (the naive circumpolar model), Mr (the regional models), and M4 (stacked generalization) models.

2.5. Model Fitting

We chose random forests [69] for our classification models, since this is an accurate, fast, and popular algorithm that usually requires little parameter tuning [70,71], and has been applied previously to estimating the distribution and habitat selection of marine vertebrates (e.g., [25,26,72]). Random forest classifiers consist of ensembles of classification trees. A single classification tree is constructed by recursive binary splitting of the predictor space using the input covariates, such that for each split (or “node”) a measure of “impurity”—in our case the Gini index—is minimized. In random forests, hundreds to thousands of these trees are grown using bootstrap samples of the training data and then, for each input case, these trees vote to determine the most popular output class [69,71]. For each split in these classification trees, only a certain number of the input covariates are randomly chosen from among all the input covariates as candidates to perform the split. This random selection of input covariates for splitting serves to decorrelate the trees, making the average (the ensemble) of all of the trees less variable and, thus, more reliable [71,73]. The importance of each input covariate is assessed by summing, for each covariate, the reduction in the Gini index due to splits using the covariate [74].

We fitted random forests with the caret [75] and ranger [76] packages. We set the number of trees to 1000, the minimum node size to 1 (default for classification [71]), used the Gini index for node splitting and assessing variable importance, and tuned the model over (i.e., selected among) three potential values of the number of covariates to possibly split at in each node (parameter “mtry”): 2, 3, and 4, these being near the recommended default of the (rounded down) square root of the number of covariates [71,73]. The number of simulated locations is much higher than the number of observed locations in our dataset (observed:simulated = 1:50) and such a class imbalance can result in classifiers achieving high performance by simply predicting the majority class. We addressed this by “undersampling” [77]—randomly downsampling the simulated locations in any model-fitting iteration to match the number of observed locations.

For both the model tuning (model parameter selection) and performance evaluation (model assessment) steps, we calculated the area under the receiver operating characteristics curve (AUC) during 10-fold cross-validation, wherein, across 10 iterations, one of the folds is held out to serve as a validation (test) set, while the remaining nine folds are used as the fitting (training) set [73,78]. We created folds by assigning individual tracks (and their associated simulated tracks) randomly into one of 10 folds, such that each fold contained an approximately equal number of individuals. This kind of stratified cross-validation yields lower AUC values than random cross-validation, but gives a more realistic (i.e., not over-optimistic) estimate of model performance for animal tracking data, given the spatio–temporal autocorrelation inherent to such data [26] (see also [79,80] for general evaluations). Since both the undersampling and cross-validation approaches involve random sampling, we repeated each cross-validation 20 times for more stable results.

We created partial dependence plots in order to visualize the relationship between the model predictions and each environmental covariate, using the DALEX package [81].

2.6. Extrapolation

To assess to what extent each regional model was being extrapolated when we predicted it circumpolarly, we used the ExDet tool [82] implemented in the dsmExtra package [83]. For each regional model, we calculated the proportion of grid cells in the circumpolar grid that were univariate extrapolations (“Type 1 novelty”, where the value of any of the covariates was outside the range of the covariates used to fit the model) and combinatorial extrapolations (“Type 2 novelty”, where the combination of covariates is novel compared to the multidimensional covariate space in which the model is fitted, assessed using Mahalanobis distance) [82,83].

2.7. Independent Validation Data

Predictive models should ideally give accurate predictions when they are confronted with new data that were not used to train the models; this is the model’s generalization performance [71], or transferability [84,85]. This is particularly important to avoid the problem of overfitting, where a model fits the training data too closely, resulting in high performance for that particular dataset, but poor performance when predicting new data (the model has low bias but high variance) [71,86]. Cross-validation (as described above) tries to deal with this problem, aiming at more generalized models, but the gold standard for validation is independent testing data that are never seen by the models during training [71]. This is often achieved by setting aside a proportion of the data before modelling, but doing so can be unrealistic when the data for modelling are already limited, as is often the case in animal tracking studies. To estimate the generalization performance of our models, we used two independent datasets on humpback whale occurrence that were not acquired via satellite telemetry, since in compiling our tracking dataset we aimed to collate essentially all available humpback whale tracking data for the Southern Ocean.

First, we used whaling catch records of humpback whales from the International Whaling Commission (IWC) catch databases, Version 6.1 [87]. We filtered the catch dataset to exclude records from land-based whaling stations, and to include only catches recorded with a spatial accuracy to the nearest degree or better, south of 40° S and taken in November–March. This resulted in 45,161 catch records from 1928–1973 (Figure 3a). Second, we used humpback whale sightings from the IWC International Decade of Cetacean Research/Southern Ocean Whale and Ecosystem Research (IDCR/SOWER) sightings database. Again, we filtered the data to include only sightings south of 40° S in November–March. This resulted in 3395 sighting records, from 1978–2010 (Figure 3b).

Model performance for these independent validation data was assessed using the probability predictions from each model in each grid cell, and whether or not a catch and/or sighting was recorded in that grid cell, with the AUC calculated using the pROC package [88].

3. Results

3.1. Regional Models

Internal cross-validation scores for the regional models (Mr) were good, with the AUC ± SD ranging from 0.711 ± 0.081–0.886 ± 0.042 (

Table 2. Model performance. Summary of the model results for (a) five circumpolar and (b) five regional models of humpback whale habitat selection. Model performance (area under the receiver operating characteristic curve: AUC) was measured by (1) internal cross-validation (CV); (2) validation against the full tracking dataset; and (3) validation against an independent dataset of whale catches and sightings. The latter represents a measure of each model’s generalization performance, and the overall model rank is based on this score. Extrapolation refers to the percentages of covariate values in the whole study area that were outside the univariate or combinatorial range of covariate values during model fitting. SD: standard deviation.

Model	Number of Tracks	Model Performance (AUC)				Rank	Extrapolation
		Internal CV	Internal CV	Validation—All Tracks	External Validation—Catches and Sightings		Univariate	Combinatorial
		(Mean)	(SD)
(a) Circumpolar models
M1	168	0.792	0.029	0.948	0.772	4	-	-
Naive circumpolar
M2	168	-	-	0.87	0.805	2	-	-
Unweighted mean
M3	168	-	-	0.937	0.764	5	-	-
Similarity-weighted mean
M4	168	0.922	0.031	0.964	0.782	3	-	-
Stacked generalization
M5	168	0.915	0.032	0.966	0.821	1	-	-
Hybrid generalization
(b) Regional models
Mr_Atlantic	41	0.886	0.042	0.685	0.702	6	1.76	0
Mr_EastIndian	15	0.806	0.084	0.743	0.677	8	6.32	0
Mr_EastPacific	62	0.711	0.081	0.628	0.628	9	0.1	0
Mr_Pacific	19	0.822	0.048	0.641	0.681	7	3.25	0
Mr_WestPacific	31	0.84	0.039	0.689	0.596	10	8.15	0.66

). However, when predicting regional models circumpolarly, they performed worse than any of the circumpolar models, according to validation with the full tracking dataset (AUC range = 0.628–0.743) and with the catches and sightings dataset (AUC range = 0.596–0.702) (Table 2). Neither the validation performance for the full tracking dataset (Spearman’s rank correlation, ρ = −0.7) nor that for the catches and sightings dataset (ρ = −0.1) were positively correlated with the number of tracks used for each regional model. Univariate extrapolation percentages ranged from 0.10%–8.15%, and the combinatorial extrapolation percentages were 0.00–0.66% (Table 2). Regional model performance was weakly correlated with univariate extrapolation percentage (ρ = 0.3) and with combinatorial extrapolation percentage (ρ = −0.1). Variable importance varied among models, but ICEDIST had the highest mean variable importance across the models (90.7), followed by SLOPEDIST (79.9), SST (79.4), and SHELFDIST (62.3) (Figure 4). Response curves indicate differences in the relationships between habitat selection and environmental covariates among regions (Supplementary Figure S1). For ICEDIST, partial dependence for the East Pacific contrasted with other regions. For SST, habitat selection decreased with increasing SST in the East Pacific and West Pacific models, contrasting with the increasing relationship in the Atlantic, East Indian, and Pacific models. SLOPEDIST and SHELFDIST showed flat partial dependence, but the habitat selection value varied among regions. Such differences were evident in the circumpolar spatial predictions of each model (Figure 1), which highlighted different areas of high habitat selectivity and, as expected from their generally high internal cross validation AUC scores (Table 2), highlighted areas where tracks were recorded (Figure 1).

3.2. Circumpolar Models

Among the circumpolar models, AUC scores based on internal cross-validation ranged from 0.792 ± 0.029 for the naive circumpolar model (M1) to 0.922 ± 0.031 for the stacked generalization (M4). Validation on all tracks yielded very high AUC scores for all models (0.937–0.966) except the unweighted mean model (M2; 0.870). AUC scores were lower when using the external validation catches and sightings data, but still reasonable (0.764–0.821). According to this metric, the hybrid generalization model (M5) was ranked first, followed by the unweighted mean model (M2). The similarity-weighted mean model (M3) performed worst among the circumpolar models by this metric (Table 2). However, the circumpolar models performed better at predicting the external validation data than any of the regional models did. Slight differences in the areas of high habitat selection were evident in the circumpolar prediction maps (Figure 5). The overall probabilities differed among models, underlining the importance of a threshold-independent performance metric such as AUC. Generally, circumpolar models highlighted waters near the sea ice edge, the coastal waters of the Antarctic Peninsula, and the migratory routes used by different populations to reach their Antarctic foraging areas (Figure 1 and Figure 5).

4. Discussion

We show how methods for incorporating regional habitat selection for a given species that is broadly distributed across a range of environmental gradients can yield models with higher predictive performance than a range-wide or large-scale model that pools the available data. In our case study using satellite telemetry data for humpback whales across the Southern Ocean, we show that three approaches lead to more accurate predictions of an independent validation dataset of humpback whale catches and sightings, compared to the naive circumpolar model. We suggest that these approaches—mean ensembles, stacked generalization, and an approach that we call hybrid generalization—can be used when more accurate predictions are sought across regional populations of animals that may show variation in habitat selection.

Extrapolating the regional models to the whole circumpolar area led to worse predictive performance on the independent validation dataset than the naive circumpolar model M1 and the ensemble models M2–M5, illustrating how regional habitat selection models may not be sufficient in situations where large-scale predictions are sought, especially when a high degree of extrapolation is required. These findings concur with studies showing limited transferability of regional habitat selection models in other large marine vertebrates (e.g., [8,9,28]). Each of these studies identified that habitat selection models fitted to animals in a given region may not adequately predict the habitat selection of animals in another region. Further, the performance of regional models in our study shows that generalization performance was not related to the amount of data or the degree of extrapolation in a straightforward way, meaning that in situations where no independent validation data are available, poor generalization performance may also go undetected, since the amount of data used, the amount of extrapolation, or the internal model performance do not indicate the generalization performance (see also [89,90]). This reflects the fact that the transferability of habitat selection models is related to many factors [84], including the ecological factors determining the specific habitat selection patterns of different animals, populations, and species. In general, however, the relationships between these factors and model transferability are not well known [84,85]. This underlines the importance of incorporating variation or heterogeneity in habitat selection among animal populations, for better inference and prediction.

Among the methods we tested for incorporating variation or heterogeneity in habitat selection, we anticipated that stacked generalization and hybrid generalization would produce the most accurate circumpolar predictions, since both approaches incorporate predictions from the regional models, but in a flexible manner that allows for complex relationships between local/regional and large-scale predictions, rather than in a linear large-scale (unweighted means) or local (similarity weighted means) manner. The stacked and hybrid generalization approaches performed similarly well for internal cross-validation, but the fact that stacked generalization performed best on the independent validation data shows that the model was not overfitting to the training data, but represents a useful approach that incorporates the environmental predictions as well as information from the regional models, leading to improved model generality (transferability). This model outperformed stacked generalization, likely because it uses not only the environmental covariates as predictors, but also the five outputs from the regional models, versus the stacked generalization model that uses only the five outputs from the regional models—a much lower dimensionality, likely representing lower information content.

Interestingly, the similarity-weighted mean model (M3) had lower predictive performance than the unweighted mean model (M2). This outcome shows that even a relatively simple method for incorporating habitat selection heterogeneity can improve predictions. In this specific case it may be that each region encompasses similar environmental gradients, the study being circumpolar. However, a similarity-weighted mean model might outperform an unweighted mean model if there is greater variance among the environmental conditions (the calibration space) in the regions being modelled. As the variation between habitats increases, the weighting of regional models in the ensemble increases, such that this method, in extreme situations, will approach a similar solution to that resulting from restricting regional models to a local spatial extent. However, the similarity-weighted mean approach still solves the problem of which model to apply in spatial areas that are located between the calibration areas, where there are no regional models or data. The method is particularly useful when the spatial proximity of regions is not a good proxy for their environmental similarity. This is because the method automates the process of calculating how close the given target environment is to the calibration environment of each candidate model, and allocates a model weighting accordingly. A possible modification to our approach would be to replace the model-predicted similarity for each grid cell with a multivariate distance measure, such as Gower’s distance (e.g., [91]). This would avoid the intermediate step of using a model to predict similarity, but could be computationally infeasible depending on the size and grain of the study area.

While our approach accounts for regional variation in habitat selection, the habitat selection of individuals may also vary consistently within regions (e.g., [92]). If this is the case, and individual-level inference or prediction is sought, methods such as mixed-effects regression can be used (e.g., [92,93].

Nevertheless, machine learning algorithms are increasingly used to model and predict the distribution of marine predators, taking advantage of the algorithms’ flexibility and high predictive power (e.g., [19,25,26,27,93,94]). For example, Becker et al. [95] reported that boosted regression trees were more accurate than generalized additive models for predicting cetacean habitat suitability, and Quillfeldt et al. [96] reported that several machine learning algorithms had higher accuracy than generalized linear models when applied to seabird tracking data. Similarly, Oppel et al. [97] found that boosted regression trees and random forests outperformed generalized linear models and generalized additive models for predicting seabird occurrence. However, machine learning algorithms may overfit, leading to overoptimistic model performance metrics and limiting their transferability (e.g., [8]). Therefore, careful fitting and validation, where possible using an independent validation dataset such as we have used here, are required [5]. Furthermore, no single algorithm will always outperform others [98].

Humpback Whale Circumpolar Habitat Selection Patterns

Variation in habitat selection patterns among the humpback whale populations suggests that the relationship between humpback whale movement behavior and environmental covariates varies among regions. Our predictions from model M5 are broadly similar to those of Bombosch et al. [99], who used 93 humpback whale sightings to model and predict circumpolar humpback whale habitat suitability. Congruence is particularly noticeable for areas downstream (east) of the Scotia Arc, in the Indian Ocean sector around 90° E, and in the Pacific sector around 140° W. These predictions highlight certain open water areas north of the sea ice edge as being highly favored habitats, as well as more northerly areas associated with migration between low-latitude breeding areas and high-latitude feeding areas. Additionally, smaller important areas are highlighted in the Sub-Antarctic. The predictions also show that key humpback whale habitats are not homogeneously distributed around Antarctica—something already indicated by whaling records [87], sightings data (e.g., [99,100]), tracking data [31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48], and other habitat modelling [99]. Similar to our validation approach, but excluding the whaling dataset, Bombosch et al. [99] used IWC sightings data corresponding with their study period as independent valuation of their predictions, achieving an AUC value of 0.877 (compared with our result of 0.821 for model M5). However, it is difficult to compare AUC values for models with different spatial extents [101]. Furthermore, this score is for monthly predictions using matching monthly validation data, versus our seasonal predictions, and our tracking dataset includes some migratory behaviors that may lower model performance slightly. Being much older than the sightings and tracking data, the whaling data present a more difficult validation challenge for models, since this involves greater temporal extrapolation. For example, there is the possibility that intensive whaling may have affected humpback whale habitat selection via broader changes to the Southern Ocean ecosystem, resulting from the removal of millions of krill predators. These could be considered drawbacks of the whaling validation data, but the positive counterpoint is that the whaling data represent a more rigorous test of model generalization. Specific biases in the IWC dataset are: (1) pelagic whaling did not primarily target humpback whales, biasing catches towards regions of higher density for other species; (2) catch effort is not equally distributed spatially, and early coastal whaling of humpbacks is not included because no at-sea positions are available for these catches; (3) catch effort varied temporally; (4) both catches and sightings are limited to relatively open waters accessible to vessels (although this latter bias is less in the case of humpback whales, which prefer areas with lower sea ice concentration [Supplementary Figure S1]); and (5) the IWC IDCR/SOWER surveys mainly targeted areas south of 60° S [99,100,102]. The IWC dataset has two general “sampling” features that affect the apparent model performance (validation AUC scores). First, as stated above, a given cell in the study area may not have been surveyed, or whaling may not have been attempted. Second, even if a given cell was sampled (surveyed or whaled), the detection of whales (sighting or catching) is imperfect. Both sampling features mean that the IWC dataset contains false absences, where a given cell contains humpback whales that are not recorded. False presences in these data are much less likely (but could increase when temporal effects, such as shifts in distribution over time, are considered). The effect of imperfect detection on species distribution models is discussed in, for example, Guillera-Arroita [103]. The false absences in the validation data we used can drive the apparent model performance downwards, when a model correctly predicts a presence in a given cell, but this correct prediction is not validated because the cell was not sampled, or because whales were missed (i.e., true positives appear to be false positives). On the other hand, apparent model performance could be driven upwards when the model incorrectly predicts an absence in a cell, but this incorrect prediction is not invalidated because the cell was not sampled, or because whales were missed (i.e., false negatives appear to be true negatives). Simulating both situations by randomly reassigning IWC presences as absences when model-predicted probability of presence was high (simulating true positives becoming false positives), or IWC absences as presences when model-predicted probability of presence was low (simulating false negatives becoming true negatives), indeed led to the expected changes in the AUC (lower and higher values, respectively) for model M5.

Previous work around the Antarctic Peninsula has shown that the distribution of prey is the primary factor for predicting humpback whale distribution and movement patterns [104,105,106]. It is likely that the circumpolar distribution of humpback whales is broadly linked to the distribution of their main prey, Antarctic krill, which themselves are inhomogeneously distributed around the continent [107,108]. The approach we detail here can be used to investigate this link more thoroughly at broader spatial scales. However, we note that in this analysis we did not distinguish migratory and putative foraging behavior, and as such our habitat selection predictions have highlighted areas associated with both of these behaviors. Future applications of this method to humpback whales could consider foraging behavior only, and models considering only a specific behavior would likely have higher performance, given that the relationship between environmental covariates and observed locations would be expected to be different for foraging versus migratory behavior.

Given that Antarctic krill distribution has shifted in some areas already [109] , and is projected to further shift by 2100 under climate change scenarios [110], our approach can also be used to project future humpback whale distribution in the Antarctic, in order to investigate potential mismatches in predator and prey distribution that could result in an ecological trap if knowledge of foraging grounds has strong inertia within populations (e.g., [111]). Despite humpback whales being highly mobile, flexible, and long-lived predators, prey changes can affect their population parameters. For example, the declining calving rate of humpback whales feeding in the Gulf of St. Lawrence, Canada, has been related to changing prey abundance [112]. Indeed, ecosystem models project that some Southern Hemisphere humpback whale populations will decline (relative to current population numbers) towards the end of the century [113].

5. Conclusions

We have shown how ensemble approaches commonly used to combine different algorithms for a single region can be reframed, treating regional habitat selection models as the candidate models. This allows the incorporation of regional variation when fitting predictive models of animal habitat selection across large ranges. We tested this approach using satellite telemetry data from 168 humpback whales across five geographic regions in the Southern Ocean and an independent validation dataset of humpback whale sightings and catches. Multiregional ensemble approaches (unweighted ensembles, stacked generalization, and hybrid generalization) resulted in models with higher predictive performance than a circumpolar naive model. These approaches can be used to incorporate regional variation in animal habitat selection when fitting range-wide predictive models using machine learning algorithms. This can yield more accurate predictions across regions or populations of animals that may show variation in habitat selection. In the case of Southern Ocean humpback whales, variation in regional habitat use patterns can be incorporated for more accurate, large-scale prediction and forecasts in support of conservation and management to mitigate the deleterious effects of human activities, including fishing and climate-driven changes, on ecosystems.