A LiDAR/Visual SLAM Backend with Loop Closure Detection and Graph Optimization
Abstract
:1. Introduction
2. System and Methods
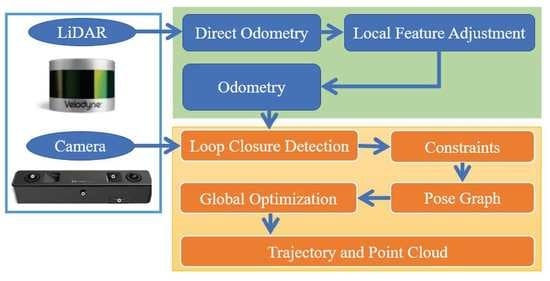
2.1. System Architecture
2.2. Loop Closure Detection
2.2.1. Visual BOW Similarity
2.2.2. Loop Closure Detection Verifying and Its Accuracy
3. Global Graph Optimization
3.1. Global Pose Construction
3.2. Globe Pose Graph Optimization
4. Experiments and Results
4.1. KITTI Dataset
4.1.1. Dataset Description
4.1.2. Results Analysis
4.2. WHU Kylin Backpack Experiment
4.2.1. Dataset Description
4.2.2. Results and Analysis
4.3. Comparisons with Google Cartographer
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bailey, T.; Durrant-Whyte, H. Simultaneous localization and mapping (SLAM): Part II. IEEE Robot. Autom. Mag. 2006, 13, 108–117. [Google Scholar] [CrossRef] [Green Version]
- Cadena, C.; Carlone, L.; Carrillo, H.; Latif, Y.; Scaramuzza, D.; Neira, J.; Reid, I.; Leonard, J.J. Past, present, and future of simultaneous localization and mapping: Toward the robust-perception age. IEEE Trans. Robot. 2016, 32, 1309–1332. [Google Scholar] [CrossRef] [Green Version]
- Zhou, B.; Ma, W.; Li, Q.; El-Sheimy, N.; Mao, Q.; Li, Y.; Zhu, J. Crowdsourcing-based indoor mapping using smartphones: A survey. ISPRS J. Photogramm. Remote Sens. 2021, 177, 131–146. [Google Scholar] [CrossRef]
- Gao, X.; Wang, R.; Demmel, N.; Cremers, D. LDSO: Direct sparse odometry with loop closure. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 2198–2204. [Google Scholar]
- Engel, J.; Koltun, V.; Cremers, D. Direct sparse odometry. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 40, 611–625. [Google Scholar] [CrossRef] [PubMed]
- Klein, G.; Murray, D. Parallel tracking and mapping for small AR workspaces. In Proceedings of the 2007 6th IEEE and ACM International Symposium on Mixed and Augmented Reality, Nara, Japan, 13–16 November 2007; pp. 225–234. [Google Scholar]
- Mur-Artal, R.; Tardos, J.D. ORB-SLAM2: An open-source SLAM system for monocular, stereo, and RGB-D cameras. IEEE Trans. Robot. 2017, 33, 1255–1262. [Google Scholar] [CrossRef] [Green Version]
- Hess, W.; Kohler, D.; Rapp, H.; Andor, D. Real-time loop closure in 2D LIDAR SLAM. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRAE), Jeju-Do, Korea, 27–29 August 2016; pp. 1271–1278. [Google Scholar]
- Zhang, J.; Singh, S. Low-drift and real-time lidar odometry and mapping. Auton. Robot. 2017, 41, 401–416. [Google Scholar] [CrossRef]
- Grisetti, G.; Stachniss, C.; Burgard, W. Improved techniques for grid mapping with rao-blackwellized particle filters. IEEE Trans. Robot. 2007, 23, 34. [Google Scholar] [CrossRef] [Green Version]
- Sturm, J.; Engelhard, N.; Endres, F.; Burgard, W.; Cremers, D. A benchmark for the evaluation of RGB-D SLAM systems. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, Vilamoura-Algarve, Portugal, 7–12 October 2012; pp. 573–580. [Google Scholar]
- Qin, T.; Li, P.; Shen, S. VINS-mono: A robust and versatile monocular visual-inertial state estimator. IEEE Trans. Robot. 2018, 34, 1004–1020. [Google Scholar] [CrossRef] [Green Version]
- Shen, S.; Michael, N.; Kumar, V. Autonomous multi-floor indoor navigation with a computationally constrained MAV. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 20–25. [Google Scholar]
- Shen, S.; Michael, N.; Kumar, V. Tightly coupled monocular visual-inertial fusion for autonomous flight of rotorcraft MAVs. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 5303–5310. [Google Scholar] [CrossRef]
- Engel, J.; Schöps, T.; Cremers, D. LSD-SLAM: Large-scale direct monocular SLAM. In Proceedings of the 13th European Conference of Computer Vision, Zürich, Switzerland, 6–12 September 2014; pp. 834–849. [Google Scholar]
- Forster, C.; Pizzoli, M.; Scaramuzza, D. SVO: Fast semi-direct monocular visual odometry. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; pp. 15–22. [Google Scholar]
- Wang, R.; Schworer, M.; Cremers, D. Stereo DSO: Large-scale direct sparse visual odometry with stereo cameras. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 3923–3931. [Google Scholar]
- Thrun, S. Probabilistic robotics. Commun. ACM 2002, 45, 52–57. [Google Scholar] [CrossRef]
- Vincent, R.; Limketkai, B.; Eriksen, M. Comparison of indoor robot localization techniques in the absence of GPS. In Detection and Sensing of Mines, Explosive Objects, and Obscured Targets XV; Harmon, R.S., Holloway, J.H., Jr., Broach, J.T., Eds.; International Society for Optics and Photonics: Bellingham, WA, USA, 2010; Volume 76641. [Google Scholar]
- Thrun, S.; Montemerlo, M. The graph SLAM algorithm with applications to large-scale mapping of urban structures. Int. J. Robot. Res. 2006, 25, 403–429. [Google Scholar] [CrossRef]
- Olson, E.B. Real-time correlative scan matching. In Proceedings of the 2009 IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; pp. 4387–4393. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Kaess, M.; Singh, S. A real-time method for depth enhanced visual odometry. Auton. Robot. 2017, 41, 31–43. [Google Scholar] [CrossRef]
- Graeter, J.; Wilczynski, A.; Lauer, M. LIMO: LiDAR-monocular visual odometry. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 7872–7879. [Google Scholar]
- Shin, Y.S.; Park, Y.S.; Kim, A. Direct visual slam using sparse depth for camera-LiDAR system. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018; pp. 5144–5151. [Google Scholar]
- Shao, W.; Vijayarangan, S.; Li, C.; Kantor, G. Stereo visual inertial LiDAR simultaneous localization and mapping. In Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Macau, China, 3–8 November 2019; pp. 370–377. [Google Scholar]
- Zhang, J.; Singh, S. Laser-visual-inertial odometry and mapping with high robustness and low drift. J. Field Robot. 2018, 35, 1242–1264. [Google Scholar] [CrossRef]
- Zhang, J.; Singh, S. Visual-lidar odometry and mapping: Low-drift, robust, and fast. Proceedings of 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 2174–2181. [Google Scholar]
- Hahnel, D.; Burgard, W.; Fox, D.; Thrun, S. An efficient FastSLAM algorithm for generating maps of large-scale cyclic environments from raw laser range measurements. In Proceedings of the 2003 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 27–31 October 2003; Volume 1, pp. 206–211. [Google Scholar]
- Beeson, P.; Modayil, J.; Kuipers, B. Factoring the mapping problem: Mobile robot map-building in the hybrid spatial semantic hierarchy. Int. J. Robot. Res. 2009, 29, 428–459. [Google Scholar] [CrossRef]
- Latif, Y.; Cadena, C.; Neira, J. Robust loop closing over time for pose graph SLAM. Int. J. Robot. Res. 2013, 32, 1611–1626. [Google Scholar] [CrossRef]
- Ulrich, I.; Nourbakhsh, I. Appearance-based place recognition for topological localization. In Proceedings of the 2000 ICRA. Millennium Conference. IEEE International Conference on Robotics and Automation, San Francisco, CA, USA, 24–28 April 2000; Volume 2, pp. 1023–1029. [Google Scholar] [CrossRef] [Green Version]
- Galvez-Lopez, D.; Tardos, J.D. Real-time loop detection with bags of binary words. In Proceedings of the 2011 IEEE/RSJ International Conference on Intelligent Robots and Systems, San Francisco, CA, USA, 25–30 September 2011; pp. 51–58. [Google Scholar]
- Galvez-Lopez, D.; Tardos, J.D. Bags of binary words for fast place recognition in image sequences. IEEE Trans. Robot. 2012, 28, 1188–1197. [Google Scholar] [CrossRef]
- Sivic, J.; Zisserman, A. Video Google: A text retrieval approach to object matching in videos. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Nice, France, 13–16 October 2003; p. 1470. [Google Scholar]
- Robertson, S. Understanding inverse document frequency: On theoretical arguments for IDF. J. Doc. 2004, 503–520. [Google Scholar] [CrossRef] [Green Version]
- Nister, D.; Stewenius, H. Scalable recognition with a vocabulary tree. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR), New York, NY, USA, 17–22 June 2006; pp. 2161–2168. [Google Scholar]


















| Detection Results Reference | True | False |
|---|---|---|
| True | True Positive | False Positive |
| False | False Negative | True Negative |
| Group | Sequences | Environment | Distance (m) | Amount of Detected Loop Closure | Accuracy (%) | Errors before GGO (m) | Errors after GGO (m) |
|---|---|---|---|---|---|---|---|
| A | #00 | Urban | 3723 | 15 | 100% | 6.71 | 0.12 |
| #05 | 2205 | 7 | 100% | 14.27 | 0.36 | ||
| B | #06 | Urban | 1232 | 6 | 100% | 0.26 | 0.27 |
| #07 | 694 | 1 | 100% | 0.29 | 0.21 | ||
| C | #02 | Urban + Rural | 5067 | 3 | 100% | 8.76 | 0.13 |
| #09 | 1705 | 1 | 100% | 0.23 | 0.09 | ||
| #08 | 3222 | 0 | - | - | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, S.; Zhou, B.; Jiang, C.; Xue, W.; Li, Q. A LiDAR/Visual SLAM Backend with Loop Closure Detection and Graph Optimization. Remote Sens. 2021, 13, 2720. https://doi.org/10.3390/rs13142720
Chen S, Zhou B, Jiang C, Xue W, Li Q. A LiDAR/Visual SLAM Backend with Loop Closure Detection and Graph Optimization. Remote Sensing. 2021; 13(14):2720. https://doi.org/10.3390/rs13142720
Chicago/Turabian StyleChen, Shoubin, Baoding Zhou, Changhui Jiang, Weixing Xue, and Qingquan Li. 2021. "A LiDAR/Visual SLAM Backend with Loop Closure Detection and Graph Optimization" Remote Sensing 13, no. 14: 2720. https://doi.org/10.3390/rs13142720
APA StyleChen, S., Zhou, B., Jiang, C., Xue, W., & Li, Q. (2021). A LiDAR/Visual SLAM Backend with Loop Closure Detection and Graph Optimization. Remote Sensing, 13(14), 2720. https://doi.org/10.3390/rs13142720