1. Introduction
In recent decades, several developed and developing countries have undergone urbanization and industrialization. This rapid development in urban areas has led to an environmental issue known as the surface urban heat island (SUHI), which affects more than half of the urban population [
1,
2,
3,
4]. SUHI is a phenomenon in which urban areas have higher surface temperatures than their suburban/rural counterparts [
5,
6,
7,
8]. Land surface temperature (LST) is a significant parameter used to explore the exchange of surface matter, surface energy balance, and surface physico-chemical processes. Thus, it is one of the most essential sources used to characterize SUHIs [
9]. LST represents the energy exchange between the land and atmosphere, an important geophysical parameter in ground–air systems [
10].
Many researchers have employed a general land cover class known as the impervious surface area (ISA) for SUHI analysis. Typically, information on the ISA information is extracted from remotely sensed images and viewed as a pure land cover class in previous studies. The ISA information used in SUHI analysis includes the ISA percentage in an image pixel [
11], ISA indices [
12], and the ISA class [
13]. The major limitation of existing studies is that the ISA is considered a pure class for analysis; here, the impact of finer ISAs on LST and their temporal variation have not yet been systematically analyzed. The ISA contains several sub-classes, including white surface, blue steel, dark metal, other dark material, and residential roofs [
14,
15]. Each sub-class is characterized by different physical properties and are the fundamental elements responsible for changes in surface energy flux [
16,
17]. The reflectance of each finer ISA class changes with the difference in the material or the building surface. For example, the reflectivity of other dark material and residential roofs is usually lower than metal and galvanized steel roofs. Additionally, the reflectivity of weathered roofs is not as high as that of newly built roofs [
18]. As such, representation of the whole ISA with only one or two classes (e.g., high albedo–low albedo, bright ISA–dark ISA, built-up area, and urban area) may be insufficient to understand the impact of finer ISAs on the LST [
19]. Similarly, different times or seasons also affect the retrieval temperature of the building roof. For example, the surface of the roof absorbs a large amount of solar radiation during the day; as such, its surface temperature is high. However, at night, without solar radiation, the roof is able to rapidly cool down and maintain a lower temperature. Moreover, the roof surface can freely exchange long-wave radiation when remote sensing images are cloud-free. The external shape of the building and the color of the roof coating also affect temperature [
18].
In this context, this study aims to examine two key aspects: (1) the distinct impacts of different building roofs (finer ISA classes) on LST, and (2) whether these particular impacts unveil temporal variations. We classified ISAs into five types of building roofs: white surface (WS), blue steel (BS), dark metal (DM), other dark material (DR), and residential roofs (RR). We also included three natural land cover types: forest, grass, and water. Multivariate regression analysis with dummy variables of ISA classes and natural land covers was used to explore the impacts of finer ISA classes on the LST. The remainder of this paper was structured into four sections.
Section 2 describes the methodology, including the study area, data source, data pre-processing method, and regression analysis.
Section 3 presents the results from analyzing four years of hot and cool seasons.
Section 4 discusses the results, and
Section 5 concludes the study.
5. Discussion
ISAs are human-made features in which water cannot infiltrate the soil; this term focuses on the physical characteristics of water infiltration. Different compositions of the ISA alter the urban surface energy budget [
19]. The assumption that all ISA classes are the same material does not accurately reflect the ISA heating properties; as such, specific drivers of urban heat retention within individual urban areas cannot be quantified [
19].
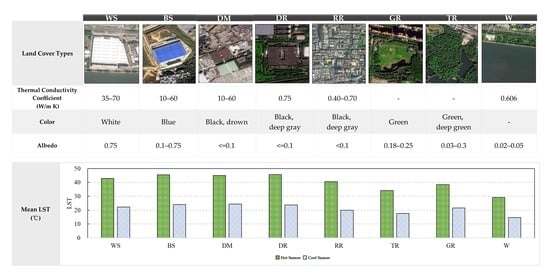
The results of this study demonstrate that various finer ISA classes showed different heat characteristics and thus differed in their contribution to LST. The LSTs of BS and DM were much higher than those of WS, RR, and the pervious surface classes. BS and DM had similar thermal conductivity coefficients around 10–60 (W/m K) at 25 °C (
Table 2) [
27]. This means they may heat up rapidly when they absorb energy from the sun. The LSTs of DR and DM were much higher than those of WS and RR; DM had the highest impact on high LST values, whereas WS showed the least heating effect as per the corresponding regression coefficients. These results may be due to their low albedo characteristics (close to 0.1); this pattern aligns with the color of absorbing heat, where black > white. Black materials are able to absorb more heat than white materials under the same environmental conditions, as white-colored materials reflect more solar energy than materials with other colors [
22,
25,
39].
The influence of different surface materials on LST varied during the hot and cool seasons. The impact magnitudes of finer ISA classes were more substantial during the cool season, although they were weaker than those of vegetation and water during the hot season (
Figure 10). Some studies have concluded that the radiation intensity of an ISA increases in the summer compared to other seasons, resulting in an increased albedo and a corresponding reduction in LST [
39,
40,
41]. By contrast, rural areas experienced an increase in temperature that was up to 0.27 °C during the summer [
42]. An additional factor that affected the LST contribution of finer classes was the moisture content of air between seasons. Air was less humid during the cool season than the hot season, reducing the surface heat capacity and increasing the surface heat radiation during the former [
43,
44]. Therefore, the contribution of finer ISAs to LST was weaker during the hot season than the cool season.
Parameters such as building density, average building height, and distance to the city center were used in the regression analysis. Most research to date has demonstrated that the horizontal and vertical differences in three-dimensional cities have an impact on LST. Many researchers have often linked building height to the urban shadow; the higher the building, the lower the temperature in this area due to the effect of shadows [
45,
46]. However, there was also a significant positive correlation between building density and LST during the hot season, and a negative correlation during the cool season. This is related to the monsoon climate, building ventilation, and human activities during different seasons [
47,
48].
There were four key limitations in this current study. First, only five types of building roofs were discussed because of the limited sample collection within the study area. Finer ISA classes, such as brick, stone, and plastic, should be collected for analysis in future studies. Second, the analysis of the impact of finer ISA classes on LST was limited to daytime imagery, particularly 11:00 a.m. local time. These impacts may vary during the afternoon or nighttime. Moreover, this research focused on the relationship between finer ISA classes and LST; however, the factors that affect urban LST are complex, including urban three-dimensional space, urban functional area distribution, and heat emissions from human activities. At the same time, LST was closely related to surface energy balance (SEB); thus, it is recommended that future research analyze the changes and driving factors of urban LST within a multi-dimensional context. Third, the analysis method used only accommodates multiple regression; as such, a new method of comparative analysis is required in future research to fully reflect the relationship between each finer roof class and the LST. Finally, shadows may have an important effect on the LST. During the sampling process, we selected samples with no or limited shadowed areas. While shadow areas were not removed during the data pre-processing stage of this study, this step should be considered in future studies.
6. Conclusions
This study discussed the impacts of finer ISA classes on LST and their temporal variations. Bar charts and ANOVA were used to demonstrate the different LST characteristics of each class. Multivariate regression models were applied to selected variables (where RR was set as the reference) during the hot and cool seasons for 2014, 2016, 2018, and 2020. The key findings from the analysis were:
- (1)
The mean LST of different types of building roofs were statistically different from each other; these differences were stronger during the hot season than the cool season. The LST of WS was significantly different from that of BS, DM, DR, and RR. The mean LSTs of BS, DM, and DR were significantly higher than those of WS and RR.
- (2)
The impacts of building roof types on the LST differed. WS, BS, DR, and DM were positively correlated with LST, while RR was negatively correlated with LST during the cool season. The impact of WS on LST was significantly different from that of BS, DR, DM, and RR. The impacts of the finer ISA classes of BS, DR, and DM on LSTs were similar; however, they demonstrated a consistent descending order pattern (i.e., DM > BS > DR >WS), during the cool season.
- (3)
The contributions of finer ISA classes to LST variance were stronger during the cool season than the hot season, as their standardized coefficients were larger in the former than the latter.
This study provides useful information to mitigate the UHI effect by unveiling specific urban heat retention drivers within urban areas. This includes different types of building roofs and pervious surface classes. This information may assist policymakers in developing effective measurements to deal with the UHI phenomenon and related health concerns.