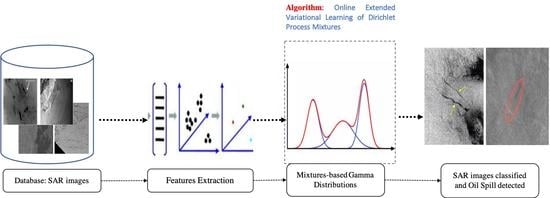
Oil Spill Detection in SAR Images Using Online Extended Variational Learning of Dirichlet Process Mixtures of Gamma Distributions
Abstract
:1. Introduction
2. Related Research Work
3. Statistical Model Specification
3.1. Finite Gamma Mixture Model
3.2. Infinite Gamma Mixture Model
4. Batch Variational Bayesian Learning
4.1. Prior Distributions for Parameters
4.2. Learning Algorithm
| Algorithm 1: Batch variational learning approach for the inGaMM |
 |
5. Online Variational Bayesian Learning
| Algorithm 2: Proposed online algorithm for inGaMM |
 |
6. Experimental Results
6.1. Data Sets
6.2. Results and Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Lary, D.J.; Alavi, A.H.; Gandomi, A.H.; Walker, A.L. Machine learning in geosciences and remote sensing. Geosci. Front. 2016, 7, 3–10. [Google Scholar] [CrossRef] [Green Version]
- Lai, Y.; Ping, Y.; He, W.; Wang, B.; Wang, J.; Zhang, X. Variational Bayesian inference for finite inverted Dirichlet mixture model and its application to object detection. Chin. J. Electron. 2018, 27, 603–610. [Google Scholar] [CrossRef]
- McLachlan, G.J.; Peel, D. Finite Mixture Models; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Andrews, J.L.; McNicholas, P.D.; Subedi, S. Model-based classification via mixtures of multivariate t-distributions. Comput. Stat. Data Anal. 2011, 55, 520–529. [Google Scholar] [CrossRef]
- Bouguila, N.; Almakadmeh, K.; Boutemedjet, S. A finite mixture model for simultaneous high-dimensional clustering, localized feature selection and outlier rejection. Expert Syst. Appl. 2012, 39, 6641–6656. [Google Scholar] [CrossRef]
- Elguebaly, T.; Bouguila, N. Background subtraction using finite mixtures of asymmetric Gaussian distributions and shadow detection. Mach. Vis. Appl. 2014, 25, 1145–1162. [Google Scholar] [CrossRef]
- Elguebaly, T.; Bouguila, N. Bayesian Learning of Generalized Gaussian Mixture Models on Biomedical Images. In Artificial Neural Networks in Pattern Recognition, Proceedings of the 4th IAPR TC3 Workshop, ANNPR 2010, Cairo, Egypt, 11–13 April 2010; Schwenker, F., Gayar, N.E., Eds.; Springer: Berlin, Germany, 2010; Volume 5998, pp. 207–218. [Google Scholar] [CrossRef] [Green Version]
- Lai, Y.; Cao, H.; Luo, L.; Zhang, Y.; Bi, F.; Gui, X.; Ping, Y. Extended variational inference for gamma mixture model in positive vectors modeling. Neurocomputing 2021, 432, 145–158. [Google Scholar] [CrossRef]
- Li, H.; Krylov, V.A.; Fan, P.; Zerubia, J.; Emery, W.J. Unsupervised Learning of Generalized Gamma Mixture Model with Application in Statistical Modeling of High-Resolution SAR Images. IEEE Trans. Geosci. Remote Sens. 2016, 54, 2153–2170. [Google Scholar] [CrossRef] [Green Version]
- Ziou, D.; Bouguila, N. Unsupervised Learning of a Finite Gamma Mixture Using MML: Application to SAR Image Analysis. In Proceedings of the 17th International Conference on Pattern Recognition, (ICPR 2004), Cambridge, UK, 23–26 August 2004; pp. 68–71. [Google Scholar] [CrossRef]
- Al-Osaimi, F.R.; Bouguila, N. A Finite Gamma Mixture Model-Based Discriminative Learning Frameworks. In Proceedings of the 14th IEEE International Conference on Machine Learning and Applications, ICMLA 2015, Miami, FL, USA, 9–11 December 2015; Li, T., Kurgan, L.A., Palade, V., Goebel, R., Holzinger, A., Verspoor, K., Wani, M.A., Eds.; IEEE: New York, NY, USA, 2015; pp. 819–824. [Google Scholar] [CrossRef]
- Beckmann, C.; Woolrich, M.; Smith, S. Gaussian/Gamma mixture modelling of ICA/GLM spatial maps. In Proceedings of the 9th International Conference on Functional Mapping of the Human Brain, New York, NY, USA, 19–22 June 2003. [Google Scholar]
- Alharithi, F.S.; Almulihi, A.H.; Bourouis, S.; Alroobaea, R.; Bouguila, N. Discriminative Learning Approach Based on Flexible Mixture Model for Medical Data Categorization and Recognition. Sensors 2021, 21, 2450. [Google Scholar] [CrossRef]
- Bourouis, S.; Channoufi, I.; Alroobaea, R.; Rubaiee, S.; Andejany, M.; Bouguila, N. Color object segmentation and tracking using flexible statistical model and level-set. Multim. Tools Appl. 2021, 80, 5809–5831. [Google Scholar] [CrossRef]
- Fan, W.; Bouguila, N.; Bourouis, S.; Laalaoui, Y. Entropy-based variational Bayes learning framework for data clustering. IET Image Process. 2018, 12, 1762–1772. [Google Scholar] [CrossRef]
- Najar, F.; Bourouis, S.; Zaguia, A.; Bouguila, N.; Belghith, S. Unsupervised Human Action Categorization Using a Riemannian Averaged Fixed-Point Learning of Multivariate GGMM. In Proceedings of the Image Analysis and Recognition—15th International Conference, ICIAR 2018, Póvoa de Varzim, Portugal, 27–29 June 2018; pp. 408–415. [Google Scholar]
- Ferguson, T.S. Bayesian density estimation by mixtures of normal distributions. In Recent Advances in Statistics; Academic Press: New York, NY, USA, 1983; pp. 287–302. [Google Scholar]
- Rasmussen, C.E. A Practical Monte Carlo Implementation of Bayesian Learning. In Proceedings of the Advances in Neural Information Processing Systems 8, NIPS, Denver, CO, USA, 27–30 November 1995; Touretzky, D.S., Mozer, M., Hasselmo, M.E., Eds.; MIT Press: Cambridge, MA, USA, 1995; pp. 598–604. [Google Scholar]
- Bourouis, S.; Alroobaea, R.; Rubaiee, S.; Andejany, M.; Almansour, F.M.; Bouguila, N. Markov Chain Monte Carlo-Based Bayesian Inference for Learning Finite and Infinite Inverted Beta-Liouville Mixture Models. IEEE Access 2021, 9, 71170–71183. [Google Scholar] [CrossRef]
- Bouguila, N.; Elguebaly, T. A fully Bayesian model based on reversible jump MCMC and finite Beta mixtures for clustering. Expert Syst. Appl. 2012, 39, 5946–5959. [Google Scholar] [CrossRef]
- Jordan, M.I.; Ghahramani, Z.; Jaakkola, T.S.; Saul, L.K. An Introduction to Variational Methods for Graphical Models. Mach. Learn. 1999, 37, 183–233. [Google Scholar] [CrossRef]
- Fan, W.; Bouguila, N. Online Learning of a Dirichlet Process Mixture of Beta-Liouville Distributions Via Variational Inference. IEEE Trans. Neural Netw. Learn. Syst. 2013, 24, 1850–1862. [Google Scholar] [CrossRef] [PubMed]
- Elguebaly, T.; Bouguila, N. A Bayesian approach for SAR images segmentation and changes detection. In Proceedings of the 2010 25th Biennial Symposium on Communications, Kingston, ON, Canada, 12–14 May 2010; pp. 24–27. [Google Scholar] [CrossRef]
- Zhao, J.; Temimi, M.; Ghedira, H.; Hu, C. Exploring the potential of optical remote sensing for oil spill detection in shallow coastal waters-a case study in the Arabian Gulf. Opt. Express 2014, 22, 13755–13772. [Google Scholar] [CrossRef]
- Singha, S.; Bellerby, T.J.; Trieschmann, O. Detection and classification of oil spill and look-alike spots from SAR imagery using an Artificial Neural Network. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, IGARSS 2012, Munich, Germany, 22–27 July 2012; pp. 5630–5633. [Google Scholar]
- Brekke, C.; Solberg, A.H. Oil spill detection by satellite remote sensing. Remote Sens. Environ. 2005, 95, 1–13. [Google Scholar] [CrossRef]
- Salberg, A.; Larsen, S.O. Classification of Ocean Surface Slicks in Simulated Hybrid-Polarimetric SAR Data. IEEE Trans. Geosci. Remote Sens. 2018, 56, 7062–7073. [Google Scholar] [CrossRef]
- Alpers, W.; Holt, B.; Zeng, K. Oil spill detection by imaging radars: Challenges and pitfalls. Remote Sens. Environ. 2017, 201, 133–147. [Google Scholar] [CrossRef]
- Solberg, A.H.S.; Storvik, G.; Solberg, R.; Volden, E. Automatic detection of oil spills in ERS SAR images. IEEE Trans. Geosci. Remote Sens. 1999, 37, 1916–1924. [Google Scholar] [CrossRef] [Green Version]
- Skrunes, S.; Brekke, C.; Eltoft, T. Characterization of Marine Surface Slicks by Radarsat-2 Multipolarization Features. IEEE Trans. Geosci. Remote Sens. 2014, 52, 5302–5319. [Google Scholar] [CrossRef] [Green Version]
- Fingas, M.; Brown, C.E. A Review of Oil Spill Remote Sensing. Sensors 2018, 18, 91. [Google Scholar] [CrossRef] [Green Version]
- Fiscella, B.; Giancaspro, A.; Nirchio, F.; Pavese, P.; Trivero, P. Oil spill detection using marine SAR images. Int. J. Remote Sens. 2000, 21, 3561–3566. [Google Scholar] [CrossRef]
- Gambardella, A.; Giacinto, G.; Migliaccio, M.; Montali, A. One-class classification for oil spill detection. Pattern Anal. Appl. 2010, 13, 349–366. [Google Scholar] [CrossRef]
- Topouzelis, K.; Karathanassi, V.; Pavlakis, P.; Rokos, D. Detection and discrimination between oil spills and look-alike phenomena through neural networks. ISPRS J. Photogramm. Remote Sens. 2007, 62, 264–270. [Google Scholar] [CrossRef]
- Karantzalos, K.; Argialas, D. Automatic detection and tracking of oil spills in SAR imagery with level set segmentation. Int. J. Remote Sens. 2008, 29, 6281–6296. [Google Scholar] [CrossRef]
- Chang, L.; Tang, Z.S.; Chang, S.H.; Chang, Y. A region-based GLRT detection of oil spills in SAR images. Pattern Recognit. Lett. 2008, 29, 1915–1923. [Google Scholar] [CrossRef]
- Solberg, A.H.S.; Brekke, C.; Husoy, P.O. Oil Spill Detection in Radarsat and Envisat SAR Images. IEEE Trans. Geosci. Remote Sens. 2007, 45, 746–755. [Google Scholar] [CrossRef]
- Keramitsoglou, I.; Cartalis, C.; Kiranoudis, C.T. Automatic identification of oil spills on satellite images. Environ. Model. Softw. 2006, 21, 640–652. [Google Scholar] [CrossRef]
- Cantorna, D.; Dafonte, C.; Iglesias, A.; Varela, B.A. Oil spill segmentation in SAR images using convolutional neural networks. A comparative analysis with clustering and logistic regression algorithms. Appl. Soft Comput. 2019, 84, 105716. [Google Scholar] [CrossRef]
- Krestenitis, M.; Orfanidis, G.; Ioannidis, K.; Avgerinakis, K.; Vrochidis, S.; Kompatsiaris, I. Oil Spill Identification from Satellite Images Using Deep Neural Networks. Remote Sens. 2019, 11, 1762. [Google Scholar] [CrossRef] [Green Version]
- Orfanidis, G.; Ioannidis, K.; Avgerinakis, K.; Vrochidis, S.; Kompatsiaris, I. A Deep Neural Network for Oil Spill Semantic Segmentation in Sar Images. In Proceedings of the 2018 IEEE International Conference on Image Processing, ICIP 2018, Athens, Greece, 7–10 October 2018; pp. 3773–3777. [Google Scholar]
- Song, D.; Ding, Y.; Li, X.; Zhang, B.; Xu, M. Ocean Oil Spill Classification with RADARSAT-2 SAR Based on an Optimized Wavelet Neural Network. Remote Sens. 2017, 9, 799. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Du, Q.; Li, Y. An efficient radial basis function neural network for hyperspectral remote sensing image classification. Soft Comput. 2016, 20, 4753–4759. [Google Scholar] [CrossRef]
- Shaban, M.; Salim, R.; Abu Khalifeh, H.; Khelifi, A.; Shalaby, A.; El-Mashad, S.; Mahmoud, A.; Ghazal, M.; El-Baz, A. A Deep-Learning Framework for the Detection of Oil Spills from SAR Data. Sensors 2021, 21, 2351. [Google Scholar] [CrossRef]
- Zeng, K.; Wang, Y. A Deep Convolutional Neural Network for Oil Spill Detection from Spaceborne SAR Images. Remote Sens. 2020, 12, 1015. [Google Scholar] [CrossRef] [Green Version]
- Topouzelis, K.N. Oil Spill Detection by SAR Images: Dark Formation Detection, Feature Extraction and Classification Algorithms. Sensors 2008, 8, 6642–6659. [Google Scholar] [CrossRef] [Green Version]
- Teh, Y.W. Dirichlet Process. In Encyclopedia of Machine Learning; Sammut, C., Webb, G.I., Eds.; Springer: Boston, MA, USA, 2010; pp. 280–287. [Google Scholar]
- Sethuraman, J. A constructive definition of Dirichlet priors. Stat. Sin. 1994, 4, 639–650. [Google Scholar]
- Blei, D.M.; Jordan, M.I. Variational inference for Dirichlet process mixtures. Bayesian Anal. 2006, 1, 121–143. [Google Scholar] [CrossRef]
- Ishwaran, H.; James, L.F. Gibbs sampling methods for stick-breaking priors. J. Am. Stat. Assoc. 2001, 96, 161–173. [Google Scholar] [CrossRef]
- Opper, M.; Saad, D. Advanced Mean Field Methods: Theory and Practice; MIT Press: Cambridge, MA, USA, 2001. [Google Scholar]
- Blei, D.M.; Jordan, M.I. Variational methods for the Dirichlet process. In Machine Learning, Proceedings of the Twenty-First International Conference (ICML 2004), Banff, AL, Canada, 4–8 July 2004; Brodley, C.E., Ed.; ACM International Conference Proceeding Series; ACM: New York, NY, USA, 2004; Volume 69. [Google Scholar]
- Sato, M. Online Model Selection Based on the Variational Bayes. Neural Comput. 2001, 13, 1649–1681. [Google Scholar] [CrossRef]
- Fan, W.; Bouguila, N. Online variational learning of generalized Dirichlet mixture models with feature selection. Neurocomputing 2014, 126, 166–179. [Google Scholar] [CrossRef]
- Hoffman, M.D.; Blei, D.M.; Bach, F.R. Online Learning for Latent Dirichlet Allocation. In Advances in Neural Information Processing Systems; Curran Associates, Inc.: New York, NY, USA, 2010; pp. 856–864. [Google Scholar]
- Manouchehri, N.; Nguyen, H.; Koochemeshkian, P.; Bouguila, N.; Fan, W. Online Variational Learning of Dirichlet Process Mixtures of Scaled Dirichlet Distributions. Inf. Syst. Front. 2020, 22, 1085–1093. [Google Scholar] [CrossRef]
- Konik, M.; Bradtke, K. Object-oriented approach to oil spill detection using ENVISAT ASAR images. ISPRS J. Photogramm. Remote Sens. 2016, 118, 37–52. [Google Scholar] [CrossRef]
- Topouzelis, K.; Psyllos, A. Oil spill feature selection and classification using decision tree forest on SAR image data. ISPRS J. Photogramm. Remote Sens. 2012, 68, 135–143. [Google Scholar] [CrossRef]
- Wang, C.; Mouche, A.; Tandeo, P.; Stopa, J.E.; Longépé, N.; Erhard, G.; Foster, R.C.; Vandemark, D.; Chapron, B. A labelled ocean SAR imagery dataset of ten geophysical phenomena from Sentinel-1 wave mode. Geosci. Data J. 2019, 6, 105–115. [Google Scholar] [CrossRef] [Green Version]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2016, Las Vegas, NV, USA, 27–30 June 2016; IEEE Computer Society: Washington, DC, USA, 2016; pp. 770–778. [Google Scholar]
- Topouzelis, K.; Stathakis, D.; Karathanassi, V. Investigation of genetic algorithms contribution to feature selection for oil spill detection. Int. J. Remote Sens. 2009, 30, 611–625. [Google Scholar] [CrossRef]
- Ferraro, G.; Pavlakis, P.; Tarchi, D.; Sieber, A.; Ferraro, G.; Vincent, G. On the Monitoring of Illicit Discharges—A Reconnaissance Study in the Mediterranean Sea; EUR 19906 EN; European Commission: Brussels, Belgium, 2001.
- Chatziantoniou, A.; Karagaitanakis, A.; Bakopoulos, V.; Papandroulakis, N.; Topouzelis, K. Detection of Biogenic Oil Films near Aquaculture Sites Using Sentinel-1 and Sentinel-2 Satellite Images. Remote Sens. 2021, 13, 1737. [Google Scholar] [CrossRef]
- Chatziantoniou, A.; Bakopoulos, V.; Papandroulakis, N.; Topouzelis, K. Detection of biogenic oil film near aquaculture sites seen by Sentinel-2 multispectral images. In Remote Sensing of the Ocean, Sea Ice, Coastal Waters, and Large Water Regions 2020; International Society for Optics and Photonics: San Diego, CA, USA, 2020; p. 4. [Google Scholar] [CrossRef]







| Datasets | No of Class | Accuracy (%) | FPR |
|---|---|---|---|
| ESA-SAR dataset | 2 | 97.96 | 0.02 |
| ESA-SAR dataset | 4 | 90.57 | 0.09 |
| Sentinel-1 wave mode SAR dataset | 2 | 94.53 | 0.05 |
| Sentinel-1 wave mode SAR dataset | 9 | 95.16 | 0.04 |
| Datasets | No of Class | Accuracy (%) | FPR |
|---|---|---|---|
| ESA-SAR dataset | 2 | 89.94 | 0.09 |
| ESA-SAR dataset | 4 | 85.13 | 0.12 |
| Sentinel-1 wave mode SAR dataset | 2 | 88.68 | 0.11 |
| Sentinel-1 wave mode SAR dataset | 9 | 82.22 | 0.14 |
| Dataset | InGaMM-eV (Our Approach) | GaMM-eV | GaMM-EM | InGMM-eV | GMM-EM |
|---|---|---|---|---|---|
| ESA-SAR | 90.05 | 88.33 | 86.07 | 83.21 | 83.11 |
| Sentinel-1 wave SAR | 91.12 | 89.40 | 87.02 | 84.14 | 83.99 |
| Dataset | InGaMM-eV (Our Approach) | GaMM-eV | GaMM-EM | InGMM-eV | GMM-EM |
|---|---|---|---|---|---|
| ESA-SAR | 88.18 | 87.09 | 85.11 | 82.13 | 82.01 |
| Sentinel-1 wave SAR | 89.12 | 88.11 | 86.00 | 83.77 | 83.07 |
| Method | Dataset | Feature Selection | Accuracy |
|---|---|---|---|
| InGaMM-eV (our approach) | ESA-SAR | ImageNet pretrained (resnet50) | 97.96% |
| InGaMM-eV (our approach) | ESA-SAR | Dark spots, geometrical, physical features | 89.94% |
| Fuzzy classification [62] | ESA-SAR | Georeference, Land masking, and Filtering | 88% |
| InGaMM-eV (our approach) | Sentinel-1 SAR | ImageNet pretrained (resnet50) | 94.53% |
| InGaMM-eV (our approach) | Sentinel-1 SAR | Dark spots, geometrical, physical features | 88.68% |
| Convolutional neural network | Sentinel-1 SAR | Inception v3 CNN | 93% |
| Articial neural network [34] | Sentinel-1 SAR | Dark spot, shape features | 87% |
| Method in [63] | Sentinel-1 SAR | Dark spot features | 81% |
| Method in [64] | Sentinel-1 SAR | Dark spot, shape features | 82.61% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Almulihi, A.; Alharithi, F.; Bourouis, S.; Alroobaea, R.; Pawar, Y.; Bouguila, N. Oil Spill Detection in SAR Images Using Online Extended Variational Learning of Dirichlet Process Mixtures of Gamma Distributions. Remote Sens. 2021, 13, 2991. https://doi.org/10.3390/rs13152991
Almulihi A, Alharithi F, Bourouis S, Alroobaea R, Pawar Y, Bouguila N. Oil Spill Detection in SAR Images Using Online Extended Variational Learning of Dirichlet Process Mixtures of Gamma Distributions. Remote Sensing. 2021; 13(15):2991. https://doi.org/10.3390/rs13152991
Chicago/Turabian StyleAlmulihi, Ahmed, Fahd Alharithi, Sami Bourouis, Roobaea Alroobaea, Yogesh Pawar, and Nizar Bouguila. 2021. "Oil Spill Detection in SAR Images Using Online Extended Variational Learning of Dirichlet Process Mixtures of Gamma Distributions" Remote Sensing 13, no. 15: 2991. https://doi.org/10.3390/rs13152991
APA StyleAlmulihi, A., Alharithi, F., Bourouis, S., Alroobaea, R., Pawar, Y., & Bouguila, N. (2021). Oil Spill Detection in SAR Images Using Online Extended Variational Learning of Dirichlet Process Mixtures of Gamma Distributions. Remote Sensing, 13(15), 2991. https://doi.org/10.3390/rs13152991