Joint Retrieval of Winter Wheat Leaf Area Index and Canopy Chlorophyll Density Using Hyperspectral Vegetation Indices
Abstract
:1. Introduction
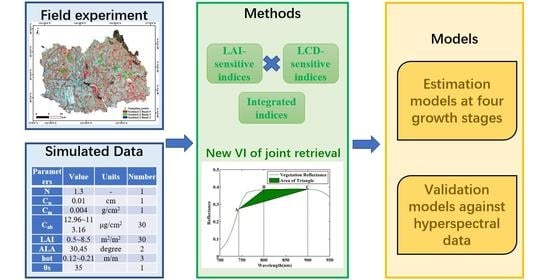
2. Materials and Methods
2.1. Study Area
2.2. Field Measurements
2.3. Simulated Spectral Datasets
2.4. Methods for Joint Retrieval
2.4.1. Vegetation Indices Used for Integration-Based Indices
2.4.2. New Indices for Joint Retrieval
2.5. Vegetation Parameters Estimation and Validation
3. Results
3.1. Estimation Models from PROSAIL Datasets
3.2. Estimation Results at Different Growth Stages
3.3. Validation
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Clevers, J.; Van Leeuwen, H. Combined use of optical and microwave remote sensing data for crop growth monitoring. Remote Sens. Environ. 1996, 56, 42–51. [Google Scholar] [CrossRef]
- Ni, J.; Zhang, J.; Wu, R.; Pang, F.; Zhu, Y. Development of an Apparatus for Crop-Growth Monitoring and Diagnosis. Sensors 2018, 18, 3129. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, J.M.; Black, T.A. Defining leaf area index for non-flat leaves. Plant Cell Environ. 1992, 15, 421–429. [Google Scholar] [CrossRef]
- Bojović, B.; Marković, A. Correlation between nitrogen and chlorophyll content in wheat (Triticum aestivum L.). Kragujev. J. Sci. 2009, 31, 69–74. [Google Scholar]
- Schlemmer, M.; Gitelson, A.; Schepers, J.; Ferguson, R.; Peng, Y.; Shanahan, J.; Rundquist, D. Remote estimation of nitrogen and chlorophyll contents in maize at leaf and canopy levels. Int. J. Appl. Earth Obs. Geoinf. 2013, 25, 47–54. [Google Scholar] [CrossRef] [Green Version]
- Broge, N.; Mortensen, J. Deriving green crop area index and canopy chlorophyll density of winter wheat from spectral reflectance data. Remote Sens. Environ. 2002, 81, 45–57. [Google Scholar] [CrossRef]
- Son, N.T.; Chen, C.F.; Chang, L.Y.; Duc, H.N.; Nguyen, L.D. Prediction of rice crop yield using MODIS EVI−LAI data in the Mekong Delta, Vietnam. Int. J. Remote Sens. 2013, 34, 7275–7292. [Google Scholar] [CrossRef]
- Thenkabail, P.S.; Smith, R.B.; De Pauw, E. Hyperspectral Vegetation Indices and Their Relationships with Agricultural Crop Characteristics. Remote Sens. Environ. 2000, 71, 158–182. [Google Scholar] [CrossRef]
- Thenkabail, P.S.; Smith, R.B.; De Pauw, E. Evaluation of narrowband and broadband vegetation indices for determining optimal hyperspectral wavebands for agricultural crop characterization. Photogramm. Eng. Remote Sens. 2002, 68, 607–622. [Google Scholar]
- Baret, F.; Guyot, G. Potentials and limits of vegetation indices for LAI and APAR assessment. Remote Sens. Environ. 1991, 35, 161–173. [Google Scholar] [CrossRef]
- Clevers, J.G.P.W.; Kooistra, L.; van den Brande, M.M.M. Using Sentinel-2 Data for Retrieving LAI and Leaf and Canopy Chlorophyll Content of a Potato Crop. Remote Sens. 2017, 9, 405. [Google Scholar] [CrossRef] [Green Version]
- Delegido, J.; Verrelst, J.; Alonso, L.; Moreno, J. Evaluation of Sentinel-2 Red-Edge Bands for Empirical Estimation of Green LAI and Chlorophyll Content. Sensors 2011, 11, 7063–7081. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Blackburn, G.A. Quantifying chlorophylls and caroteniods at leaf and canopy scales: An evaluation of some hyperspectral approaches. Remote Sens. Environ. 1998, 66, 273–285. [Google Scholar] [CrossRef]
- Clevers, J.G.; Kooistra, L. Using hyperspectral remote sensing data for retrieving canopy chlorophyll and nitrogen content. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2011, 5, 574–583. [Google Scholar] [CrossRef]
- Fang, H.; Liang, S. Retrieving leaf area index with a neural network method: Simulation and validation. IEEE Trans. Geosci. Remote Sens. 2003, 41, 2052–2062. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.; Jin, X.; Wang, J.; Yang, G.; Nie, C.; Xu, X.; Feng, H. Estimating winter wheat (Triticum aestivum) LAI and leaf chlorophyll content from canopy reflectance data by integrating agronomic prior knowledge with the PROSAIL model. Int. J. Remote Sens. 2015, 36, 2634–2653. [Google Scholar] [CrossRef]
- Dong, T.; Liu, J.; Shang, J.; Qian, B.; Ma, B.; Kovacs, J.M.; Walters, D.; Jiao, X.; Geng, X.; Shi, Y. Assessment of red-edge vegetation indices for crop leaf area index estimation. Remote Sens. Environ. 2019, 222, 133–143. [Google Scholar] [CrossRef]
- Li, W.; Weiss, M.; Waldner, F.; Defourny, P.; Demarez, V.; Morin, D.; Hagolle, O.; Baret, F. A Generic algorithm to estimate LAI, FAPAR and FCOVER variables from SPOT4_HRVIR and landsat sensors: Evaluation of the consistency and comparison with ground measurements. Remote Sens. 2015, 7, 15494–15516. [Google Scholar] [CrossRef] [Green Version]
- Eriksson, H.; Eklundh, L.; Hall, K.; Lindroth, A. Estimating LAI in deciduous forest stands. Agric. For. Meteorol. 2005, 129, 27–37. [Google Scholar] [CrossRef]
- Kawashima, S.; Nakatani, M. An algorithm for estimating chlorophyll content in leaves using a video camera. Ann. Bot. 1998, 81, 49–54. [Google Scholar] [CrossRef] [Green Version]
- Gitelson A, A. Wide dynamic range vegetation index for remote quantification of biophysical characteristics of vegetation. J. Plant Physiol. 2004, 161, 165–173. [Google Scholar] [CrossRef] [Green Version]
- Daughtry, C.S.T.; Walthall, C.L.; Kim, M.S.; De Colstoun, E.B.; McMurtrey, J.E. Estimating Corn Leaf Chlorophyll Concentration from Leaf and Canopy Reflectance. Remote Sens. Environ. 2000, 74, 229–239. [Google Scholar] [CrossRef]
- Blackburn, G.A. Spectral indices for estimating photosynthetic pigment concentrations: A test using senescent tree leaves. Int. J. Remote Sens. 1998, 19, 657–675. [Google Scholar] [CrossRef]
- Xing, N.; Huang, W.; Xie, Q.; Shi, Y.; Ye, H.; Dong, Y.; Wu, M.; Sun, G.; Jiao, Q. A transformed triangular vegetation index for estimating winter wheat leaf area index. Remote Sens. 2020, 12, 16. [Google Scholar] [CrossRef] [Green Version]
- Haboudane, D.; Miller, J.R.; Pattey, E.; Zarco-Tejada, P.J.; Strachan, I.B. Hyperspectral vegetation indices and novel algorithms for predicting green LAI of crop canopies: Modeling and validation in the context of precision agriculture. Remote Sens. Environ. 2004, 90, 337–352. [Google Scholar] [CrossRef]
- Rondeaux, G.; Steven, M.; Baret, F. Optimization of Soil-Adjusted Vegetation Indices. Remote Sens. Environ. 1996, 55, 95–107. [Google Scholar] [CrossRef]
- Dash, J.; Curran, P.J. The MERIS terrestrial chlorophyll index. Int. J. Remote Sens. 2004, 25, 5403–5413. [Google Scholar] [CrossRef]
- Cui, B.; Zhao, Q.; Huang, W.; Song, X.; Ye, H.; Zhou, X. A new integrated vegetation index for the estimation of winter wheat leaf chlorophyll content. Remote Sens. 2019, 11, 974. [Google Scholar] [CrossRef] [Green Version]
- Banerjee, V.; Krishnan, P.; Das, B.; Verma, A.; Varghese, E. Crop Status Index as an indicator of wheat crop growth condition under abiotic stress situations. Field Crops Res. 2015, 181, 16–31. [Google Scholar] [CrossRef]
- Houborg, R.; McCabe, M.; Cescatti, A.; Gao, F.; Schull, M.; Gitelson, A. Joint leaf chlorophyll content and leaf area index retrieval from Landsat data using a regularized model inversion system (REGFLEC). Remote Sens. Environ. 2015, 159, 203–221. [Google Scholar] [CrossRef] [Green Version]
- Haboudane, D.; Miller, J.R.; Tremblay, N.; Zarco-Tejada, P.J.; Dextraze, L. Integrated narrow-band vegetation indices for prediction of crop chlorophyll content for application to precision agriculture. Remote Sens. Environ. 2002, 81, 416–426. [Google Scholar] [CrossRef]
- Delegido, J.; Verrelst, J.; Meza, C.; Rivera, J.; Alonso, L.; Moreno, J. A red-edge spectral index for remote sensing estimation of green LAI over agroecosystems. Eur. J. Agron. 2013, 46, 42–52. [Google Scholar] [CrossRef]
- Chang-Hua, J.; Yong-Chao, T.I.A.N.; Xia, Y.A.O.; Wei-Xing, C.A.O.; Yan, Z.H.U.; Hannaway, D. Estimating leaf chlorophyll content using red edge parameters. Pedosphere 2010, 20, 633–644. [Google Scholar]
- Sharma, L.K.; Bu, H.; Denton, A.; Franzen, D.W. Active-Optical Sensors Using Red NDVI Compared to Red Edge NDVI for Prediction of Corn Grain Yield in North Dakota, U.S.A. Sensors 2015, 15, 27832–27853. [Google Scholar] [CrossRef]
- Kanke, Y.; Tubaña, B.; Dalen, M.; Harrell, D. Evaluation of red and red-edge reflectance-based vegetation indices for rice biomass and grain yield prediction models in paddy fields. Precis. Agric. 2016, 17, 507–530. [Google Scholar] [CrossRef]
- Zhou, X.; Huang, W.; Kong, W.; Ye, H.; Dong, Y.; Casa, R. Assessment of leaf carotenoids content with a new carotenoid index: Development and validation on experimental and model data. Int. J. Appl. Earth Obs. Geoinf. 2017, 57, 24–35. [Google Scholar] [CrossRef]
- Gao, J. Experimental Guidance for Plant Physiology; China Higher Education Press: Beijing, China, 2006. [Google Scholar]
- Verrelst, J.; Camps-Valls, G.; Muñoz-Marí, J.; Rivera, J.P.; Veroustraete, F.; Clevers, J.; Moreno, J. Optical remote sensing and the retrieval of terrestrial vegetation bio-geophysical properties—A review. ISPRS J. Photogramm. Remote Sens. 2015, 108, 273–290. [Google Scholar] [CrossRef]
- Jacquemoud, S.; Verhoef, W.; Baret, F.; Bacour, C.; Zarco-Tejada, P.J.; Asner, G.P.; François, C.; Ustin, S.L. PROSPECT+SAIL models: A review of use for vegetation characterization. Remote Sens. Environ. 2009, 113, S56–S66. [Google Scholar] [CrossRef]
- Li, Z.; Jin, X.; Yang, G.; Drummond, J.; Yang, H.; Clark, B.; Li, Z.; Zhao, C. Remote sensing of leaf and canopy nitrogen status in winter wheat (Triticum aestivum L.) based on N-PROSAIL model. Remote Sens. 2018, 10, 1463. [Google Scholar] [CrossRef] [Green Version]
- Xie, Q.; Dash, J.; Huete, A.; Jiang, A.; Yin, G.; Ding, Y.; Peng, D.; Hall, C.C.; Brown, L.; Shi, Y.; et al. Retrieval of crop biophysical parameters from Sentinel-2 remote sensing imagery. Int. J. Appl. Earth Obs. Geoinf. 2019, 80, 187–195. [Google Scholar] [CrossRef]
- Duveiller, G.; Weiss, M.; Baret, F.; Defourny, P. Retrieving wheat Green Area Index during the growing season from optical time series measurements based on neural network radiative transfer inversion. Remote Sens. Environ. 2011, 115, 887–896. [Google Scholar] [CrossRef]
- Fang, H.; Baret, F.; Plummer, S.; Schaepman-Strub, G. An overview of global leaf area index (LAI): Methods, products, validation, and applications. Rev. Geophys. 2019, 57, 739–799. [Google Scholar] [CrossRef]
- Xie, Q.; Huang, W.; Zhang, B.; Chen, P.; Song, X.; Pascucci, S.; Pignatti, S.; Laneve, G.; Dong, Y. Estimating Winter Wheat Leaf Area Index From Ground and Hyperspectral Observations Using Vegetation Indices. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 9, 771–780. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Gritz, Y.; Merzlyak, M.N. Relationships between leaf chlorophyll content and spectral reflectance and algorithms for non-destructive chlorophyll assessment in higher plant leaves. J. Plant Physiol. 2003, 160, 271–282. [Google Scholar] [CrossRef]
- Babar, M.A.; Reynolds, M.P.; Van Ginkel, M.; Klatt, A.R.; Raun, W.; Stone, M.L. Spectral Reflectance to Estimate Genetic Variation for In-Season Biomass, Leaf Chlorophyll, and Canopy Temperature in Wheat. Crop Sci. 2006, 46, 1046–1057. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Keydan, G.P.; Merzlyak, M.N. Three-band model for noninvasive estimation of chlorophyll, carotenoids, and anthocyanin contents in higher plant leaves. Geophys. Res. Lett. 2006, 33, L11402. [Google Scholar] [CrossRef] [Green Version]
- Gitelson, A.A.; Viña, A.; Ciganda, V.; Rundquist, D.C.; Arkebauer, T.J. Remote estimation of canopy chlorophyll content in crops. Geophys. Res. Lett. 2005, 32, L08403. [Google Scholar] [CrossRef] [Green Version]
- Wu, C.; Niu, Z.; Tang, Q.; Huang, W. Estimating chlorophyll content from hyperspectral vegetation indices: Modeling and validation. Agric. For. Meteorol. 2008, 148, 1230–1241. [Google Scholar] [CrossRef]
- Gamon, J.A.; Surfus, L.S.S. The Photochemical Reflectance Index: An Optical Indicator of Photosynthetic Radiation Use Efficiency across Species, Functional Types, and Nutrient Levels. Oecologia 1997, 112, 492–501. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Gamon, J.A.; Solovchenko, A. Multiple drivers of seasonal change in PRI: Implications for photosynthesis 2. Stand level. Remote Sens. Environ. 2017, 190, 198–206. [Google Scholar] [CrossRef] [Green Version]
- Tucker, C.J. Red and photographic infrared linear combinations for monitoring vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar] [CrossRef] [Green Version]
- Clevers, J.G.; De Jong, S.; Epema, G.F.; van der Meer, F.; Bakker, W.H.; Skidmore, A.; Addink, E. MERIS and the red-edge position. Int. J. Appl. Earth Obs. Geoinf. 2001, 3, 313–320. [Google Scholar] [CrossRef]
- Lay, D.C.; Lay, S.R.; McDonald, J.J. Linear Algebra and Its Applications; Pearson: London, UK, 2016. [Google Scholar]
- Malenovský, Z.; Homolová, L.; Zurita-Milla, R.; Lukeš, P.; Kaplan, V.; Hanuš, J.; Gastellu-Etchegorry, J.P.; Schaepman, M.E. Retrieval of spruce leaf chlorophyll content from airborne image data using continuum removal and radiative transfer. Remote Sens. Environ. 2013, 131, 85–102. [Google Scholar] [CrossRef] [Green Version]
- Xie, Q.; Dash, J.; Huang, W.; Peng, D.; Qin, Q.; Mortimer, H.; Casa, R.; Pignatti, S.; Laneve, G.; Pascucci, S.; et al. Vegetation Indices Combining the Red and Red-Edge Spectral Information for Leaf Area Index Retrieval. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 1482–1493. [Google Scholar] [CrossRef] [Green Version]
- Broge, N.H.; Leblanc, E. Comparing prediction power and stability of broadband and hyperspectral vegetation indices for estimation of green leaf area index and canopy chlorophyll density. Remote Sens. Environ. 2001, 76, 156–172. [Google Scholar] [CrossRef]
- Le Maire, G.; François, C.; Dufrêne, E. Towards universal broad leaf chlorophyll indices using PROSPECT simulated database and hyperspectral reflectance measurements. Remote Sens. Environ. 2004, 89, 1–28. [Google Scholar] [CrossRef]
- Hao, D.; Wen, J.; Xiao, Q.; Wu, S.; Lin, X.; You, D.; Tang, Y. Modeling Anisotropic Reflectance Over Composite Sloping Terrain. IEEE Trans. Geosci. Remote Sens. 2018, 56, 3903–3923. [Google Scholar] [CrossRef]
- Kumari, N.; Saco, P.M.; Rodriguez, J.F.; Johnstone, S.A.; Srivastava, A.; Chun, K.P.; Yetemen, O. The Grass Is Not Always Greener on the Other Side: Seasonal Reversal of Vegetation Greenness in Aspect-Driven Semiarid Ecosystems. Geophys. Res. Lett. 2020, 47, e2020GL088918. [Google Scholar] [CrossRef]
- Matsushita, B.; Yang, W.; Chen, J.; Onda, Y.; Qiu, G. Sensitivity of the Enhanced Vegetation Index (EVI) and Normalized Difference Vegetation Index (NDVI) to Topographic Effects: A Case Study in High-density Cypress Forest. Sensors 2007, 7, 2636–2651. [Google Scholar] [CrossRef] [Green Version]
- Kaufman, Y.; Tanre, D. Atmospherically resistant vegetation index (ARVI) for EOS-MODIS. IEEE Trans. Geosci. Remote Sens. 1992, 30, 261–270. [Google Scholar] [CrossRef]








| Growth Stages. | Total Sample Plots | Selected Sample Plots |
|---|---|---|
| Early jointing stage | 24 | 18 |
| Late jointing stage | 24 | 18 |
| Head emergence stage | 24 | 18 |
| Filling stage | 24 | 18 |
| Pooled | 96 | 72 |
| Parameters | Notes | Value | Distribution | Units | Number |
|---|---|---|---|---|---|
| Leaf parameters | |||||
| N | Leaf structure parameter | 1.3 | Gaussian | - | 1 |
| Cw | Water content | 0.01 | cm | 1 | |
| Cm | Dry matter content | 0.004 | g/cm2 | 1 | |
| Cab | Chlorophyll a + b content | 12.96~113.16 | Gaussian standard deviation of 50, mean value of 50 | μg/cm2 | 30 |
| Canopy parameters | |||||
| LAI | Leaf area index | 0.5~8.5 | Uniform | m2/m2 | 30 |
| ALA | Average leaf angle | 30,45 | degree | 2 | |
| hot | Hot spot parameter | 0.12~0.21 | Uniform | m/m | 3 |
| θs | Solar zenith angle | 35 | 1 | ||
| Index | Description | Calculation | Related to | Reference |
|---|---|---|---|---|
| DVI | Difference vegetation index | LAI | [52] | |
| NDVI | Normalized difference vegetation index | LAI | [23] | |
| TVI | Triangular vegetation index | LAI | [25] | |
| TTVI | Transformed triangular vegetation index | LAI | [24] | |
| PSSRa | Pigment-specific simple ratio | CCD | [13] | |
| CIred-edge | Red-edge chlorophyll index | CCD | [45,47] | |
| RES | Red edge symmetry | CCD | [33] | |
| PRI | Photochemical reflectance index | LAI, CCD | [50] | |
| MCARI | Modified chlorophyll absorption ratio index | CCD | [25] | |
| MSAVI | Modified soil-adjusted vegetation index | LAI | [25] |
| Vegetation Indices | Equations | R2 | |
|---|---|---|---|
| Indices sensitive to LAI | DVI | LAI = 17.359x − 3.2295 | R2 = 0.77 |
| CCD = 13.805exp(5.6679x) | R2 = 0.61 | ||
| NDVI | LAI = 0.0508exp(4.9621x) | R2 = 0.84 | |
| CCD = 1.7412exp(5.3067x) | R2 = 0.66 | ||
| TVI | LAI = 0.4118exp(0.0936x) | R2 = 0.73 | |
| CCD = 29.572exp(0.0735x) | R2 = 0.31 | ||
| TTVI | LAI = 0.7212x + 0.8171 | R2 = 0.64 | |
| CCD = 58.487x − 57.855 | R2 = 0.93 | ||
| Indices sensitive to chlorophyll content | PSSRa | LAI = 0.1895x + 0.3459 | R2 = 0.84 |
| CCD = 39.318exp(0.068x) | R2 = 0.78 | ||
| CIred-edge | LAI = 2.2074ln(x) + 1.809 | R2 = 0.45 | |
| CCD = 65.064x − 22.27 | R2 = 0.91 | ||
| Indices for joint retrieval | PRI | LAI = 1.5749exp(59.885x) | R2 = 0.97 |
| CCD = 72.208exp(59.885x) | R2 = 0.67 | ||
| CIred-edge×NDVI | LAI = 1.9344ln(x) + 2.4569 | R2 = 0.51 | |
| CCD = 66.614x − 3.4656 | R2 = 0.92 | ||
| CIred-edge×TVI | LAI = 1.9757ln(x) − 3.978 | R2 = 0.62 | |
| CCD = 2.5883x − 8.544 | R2 = 0.93 | ||
| CIred-edge×TTVI | LAI = 1.2541ln(x) + 1.1513 | R2 = 0.55 | |
| CCD = 6.2787x + 72.157 | R2 = 0.93 | ||
| CIred-edge×PSSRa | LAI = 1.3206ln(x) − 0.8848 | R2 = 0.66 | |
| CCD = 1.735x + 52.04 | R2 = 0.94 | ||
| CIred-edge×MSAVI | LAI = 1.8228ln(x) + 2.9543 | R2 = 0.58 | |
| CCD = 72.364x + 10.192 | R2 = 0.94 | ||
| CIred-edge×MCARI | LAI= 1.5191ln(x) + 7.1729 | R2 = 0.48 | |
| CCD = 123.48exp(0.9887x) | R2 = 0.04 | ||
| CIred-edge×PRI | LAI = 9.6612x + 2.5863 | R2 = 0.68 | |
| CCD = 683.65x + 101.39 | R2 = 0.75 | ||
| RES×NDVI | LAI = −0.657ln(x) + 3.3084 | R2 = 0.01 | |
| CCD = −354.9ln(x) − 225.45 | R2 = 0.38 | ||
| RES×TVI | LAI = 2.0488exp(0.0589x) | R2 = 0.08 | |
| CCD = −123.5ln(x) + 458.13 | R2 = 0.10 | ||
| RES×TTVI | LAI = 0.5659exp(1.225x) | R2 = 0.85 | |
| CCD = 21.232exp(1.364x) | R2 = 0.72 | ||
| RES×PSSRa | LAI = 0.9024exp(0.1997x) | R2 = 0.78 | |
| CCD = 54.284exp(0.158x) | R2 = 0.34 | ||
| RES×MSAVI | LAI = 1.3865exp(3.5257x) | R2 = 0.14 | |
| CCD = −542.55x + 343.47 | R2 = 0.07 | ||
| RES×MCARI | LAI = 3.0636exp(2.0307x) | R2 = 0.02 | |
| CCD = −62.16ln(x) − 45.108 | R2 = 0.29 | ||
| RES×PRI | LAI = 2.666exp(31.215x) | R2 = 0.79 | |
| CCD = 126.79exp(25.946x) | R2 = 0.37 | ||
| TTVI2 | LAI = 0.6796x + 0.8802 | R2 = 0.63 | |
| CCD = 55.897x − 56.483 | R2 = 0.95 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xing, N.; Huang, W.; Ye, H.; Ren, Y.; Xie, Q. Joint Retrieval of Winter Wheat Leaf Area Index and Canopy Chlorophyll Density Using Hyperspectral Vegetation Indices. Remote Sens. 2021, 13, 3175. https://doi.org/10.3390/rs13163175
Xing N, Huang W, Ye H, Ren Y, Xie Q. Joint Retrieval of Winter Wheat Leaf Area Index and Canopy Chlorophyll Density Using Hyperspectral Vegetation Indices. Remote Sensing. 2021; 13(16):3175. https://doi.org/10.3390/rs13163175
Chicago/Turabian StyleXing, Naichen, Wenjiang Huang, Huichun Ye, Yu Ren, and Qiaoyun Xie. 2021. "Joint Retrieval of Winter Wheat Leaf Area Index and Canopy Chlorophyll Density Using Hyperspectral Vegetation Indices" Remote Sensing 13, no. 16: 3175. https://doi.org/10.3390/rs13163175
APA StyleXing, N., Huang, W., Ye, H., Ren, Y., & Xie, Q. (2021). Joint Retrieval of Winter Wheat Leaf Area Index and Canopy Chlorophyll Density Using Hyperspectral Vegetation Indices. Remote Sensing, 13(16), 3175. https://doi.org/10.3390/rs13163175