A Comparison of ALS and Dense Photogrammetric Point Clouds for Individual Tree Detection in Radiata Pine Plantations

Abstract

Digital aerial photogrammetry (DAP) has emerged as a potentially cost-effective alternative to airborne laser scanning (ALS) for forest inventory methods that employ point cloud data. Forest inventory derived from DAP using area-based methods has been shown to achieve accuracy similar to that of ALS data. At the tree level, individual tree detection (ITD) algorithms have been developed to detect and/or delineate individual trees either from ALS point cloud data or from ALS- or DAP-based canopy height models. An examination of the application of ITDs to DAP-based point clouds has not yet been reported. In this research, we evaluate the suitability of DAP-based point clouds for individual tree detection in the Pinus radiata plantation. Two ITD algorithms designed to work with point cloud data are applied to dense point clouds generated from small- and medium-format photography and to an ALS point cloud. Performance of the two ITD algorithms, the influence of stand structure on tree detection rates, and the relationship between tree detection rates and canopy structural metrics are investigated. Overall, we show that there is a good agreement between ALS- and DAP-based ITD results (proportion of false negatives for ALS, SFP, and MFP was always lower than 29.6%, 25.3%, and 28.6%, respectively, whereas, the proportion of false positives for ALS, SFP, and MFP was always lower than 39.4%, 30.7%, and 33.7%, respectively). Differences between small- and medium-format DAP results were minor (for SFP and MFP, differences between recall, precision, and F-score were always less than 0.08, 0.03, and 0.05, respectively), suggesting that DAP point cloud data is robust for ITD. Our results show that among all the canopy structural metrics, the number of trees per hectare has the greatest influence on the tree detection rates.

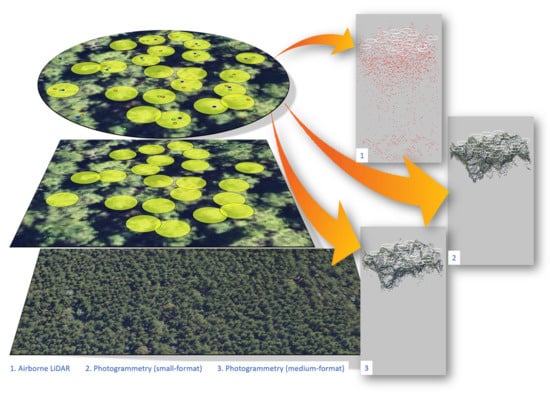
1. Introduction

Forest inventory has greatly benefitted from the emergence and ongoing development of airborne laser scanning (ALS). The potential of wide area, contiguous sampling of forest structure using a technology that achieves high point density, high vertical accuracy, and that has high penetrative capacity was recognised early in the commercialisation of ALS [1] and has been the subject of very extensive research and increasingly widespread application [2]. Numerous studies have demonstrated that ALS can be used to reliably estimate forest inventory attributes such as basal area, canopy height, volume, and stocking (tree stems per hectare) [3,4,5] and that ALS is suitable for operational forest inventory [6,7,8].

Generally, one of two approaches are used to estimate ALS-based forest inventory: (i) an area-based approach (ABA) (e.g., [9]) or (ii) an individual tree detection (ITD) approach (e.g., [10,11]). In ABA, statistics describing the horizontal and vertical characteristics of canopies are extracted from point cloud data and modelled against spatially coincident ground-based plot data. A predictive model is then applied to the entire area of interest to estimate plot- and stand-level forest inventory attributes such as top height, stocking, basal area, and timber volume [2,12,13]. In an ITD approach, the tops of individual trees are identified using an automated or a semi-automated approach, and then often followed by tree-crown delineation to extract tree-level attributes such as tree height, crown diameter, canopy closure, and stocking. An ITD approach is attractive to forest managers when high-resolution inventory is desired, such as acquiring attributes for each tree and subsequent derivation of stem distribution [14], growth modelling [15,16], and precise measures of tree volume and forest biomass [17,18].

A variety of statistical models and algorithms have been developed to estimate area-based and individual tree-based inventory [19,20,21]. When compared, results from each of the two approaches are generally in close agreement when the basal area, volume, mean height, mean diameter, and aboveground carbon density are estimated [22,23,24,25]. However large differences have been reported when stocking, which is of particular interest and relevance to this study, is estimated. For example, using ALS data, Peuhkurinen et al. [22] reported that overall ABA-based estimates of stocking were better than ITD by about 30%, although Rahlf et al. [26] using a raster surface derived from DAP-based point cloud data reported that ITD-based estimates of stocking were better than ABA by 5%. A common finding is that ITD-based estimates can be significantly biased [22,26]. Differences between the stocking estimates of these two studies can in part be attributed to different data characteristics, the variability in forest structure and condition [27,28], and the choice and parameterisation of the ITD method [21].

Several algorithms have been developed to detect individual treetops or delineate tree crowns [29,30]. Broadly, based on the input data, these algorithms can be categorised into (i) raster-based (e.g., [31]) and (ii) point cloud based (e.g., [32]) algorithms. Raster-based algorithms take a Canopy Height Model (CHM) derived from interpolated point clouds as an input. Treetops are then located in the CHM using e.g., a local maxima filter within a user-defined search window, followed by a region-growing algorithm to delineate tree crowns [17,33]. Uncertainties and errors in generating the CHM are highly likely to influence the treetop identification and crown delineation [34]. Also, it is to be expected that suppressed trees may not be registered in the CHM, which is typically generated using ALS first returns [21]. Point cloud based algorithms have the potential to be more reliable, especially when detection of suppressed trees is desired, as they use the actual/raw point clouds rather than an interpolated CHM [35] and so reduce the risk of errors introduced by the interpolation process [32,36]. Point cloud based algorithms, however, can be computationally intensive depending on the volume of data [37].

Individual tree detection methods have been applied to ALS point clouds acquired over a variety of forest conditions and significant variations in detection rates reported [21,28,35,38,39]. Kaartinen et al. [21] applied thirteen ITD methods to two managed forest sites in Southern Finland, with trees at various developmental stages. Forest stands varied structurally from relatively homogenous coniferous or deciduous to mixed forests. Overall, the percentage of detected trees ranged from 25% to 102%. Tree detection accuracies were relatively better in the dominant heights (55–98%) than in sub-dominant heights. Vauhkonen et al. [28] studied the effect of five different forest conditions (located in Brazil, Germany, Norway, and Sweden) on the detection accuracy of six different ITD algorithms. In all forest conditions, the percentage of detected trees varied among the algorithms: 63–97% (in Brazil), 49–100% (in Germany), 45–68% (in Norway), and 65–86% (in Sweden). Eysn et al. [35] compared eight ITD algorithms in Alpine forests (in Austria, France, Italy, Slovenia, and Switzerland), with species composition varying from single-layered coniferous to multi-layered mixed forests. Tree detection accuracy was the highest in single-layered coniferous forest and ranged from about 52–70% among the ITD algorithms. In the same study area as in Kaartinen et al. [21], Wang et al. [38] evaluated the accuracy of five ITD methods in four different crown classes (dominant, co-dominant, intermediate, and suppressed). The highest tree detection accuracy was recorded for the dominant crown class (70–95%). Unlike ABAs, in which RMSE and bias are used as ‘standard’ accuracy assessment methods, ITD results reported in the literature are on different scales, which means that they should be compared with care [40].

Although the detection rates reported in the above-mentioned studies were different, there is a broad agreement that the performance of ITD is mainly driven by stand variability (homogeneous vs. heterogeneous), diversity in vertical structure (canopy layers), the choice and parameterisation of the ITD method, and that tree detection accuracy is usually higher in dominant and co-dominant canopy strata. Wang et al. [38] found that the influence of vertical structure on ITD was more significant than that of tree species. Kaartinen et al. [21] and Wang et al. [38] concluded that ALS point density has little influence on ITD accuracy, particularly in dominant and co-dominant canopy layers.

More recently, digital aerial photogrammetry (DAP) has emerged as a potentially cost-effective alternative to ALS. Dense point clouds are generated from high-overlap DAP [41] using Structure from Motion-Multi View Stereopsis (SfM-MVS) [42] and there is now a strong base of evidence that it can be treated in a similar way as ALS point clouds to estimate forest inventory attributes (e.g., [12,43,44]). Compared with ALS, DAP-based point cloud data have substantially higher point density and comparable or higher spatial accuracy [45]. However, because DAP-based point clouds are generated from multiple overlapping imageries, their penetrative ability is limited and highly influenced by factors including canopy structure (i.e., the horizontal and vertical distribution of branches and foliage), canopy illumination, and the geometry of photography (flying height, percentage of overlap, view angle, focal length, and image format) [12,45,46]. Moreover, DAP-based point cloud data usually rely on a separately acquired digital terrain model (DTM) for normalisation to remove the height of underlying terrain from each point in the cloud. Various studies have demonstrated that inventory estimates derived from DAP-based point cloud data were in good agreement with ALS-based estimates in a variety of forest environments [3,13,47,48,49].

A small number of studies have applied ITD approaches to photogrammetrically derived canopy data and have reported promising results when compared with ALS data. For example, St-Onge et al. [50] applied a raster-based (CHM) ITD approach to a raster canopy surface derived from a DAP-based point cloud and characterised species composition and tree height distribution in a boreal forest in Canada. They obtained similar results with raster surfaces derived from both DAP-based and ALS point clouds. Goldbergs et al. [51] acquired DAP from an Unmanned Aerial Vehicle (UAV) and applied raster-based ITD approaches to a raster canopy surface derived from DAP-based point cloud to detect individual (Eucalyptus spp.) trees, measure tree heights and provide aboveground biomass estimates in northern Australia. They found that the overall tree detection accuracy of the DAP-based point cloud was less than that of the ALS by only about 10%. Similarly, Guerra-Hernández et al. [52] employed a CHM-based ITD approach using surfaces derived from UAV-based DAP and ALS to compare tree detection rates in a Eucalyptus spp. plantation in Portugal. They reported that the percentage of detected trees for the DAP-derived surface was less than that for the ALS by about 16%. More recently, Kwong & Fung [53], in Tai Po Kau Park Hong Kong, applied a CHM-based ITD approach to rasterised surfaces derived from point cloud data sourced from UAV, traditional large-format aerial photography, and from ALS, concluding no clear preference of one data over the other. In these studies, only raster-based ITD approaches have been applied to the DAP-based point cloud.

To our knowledge, an examination of the application of point cloud based ITDs to DAP-based point clouds has not yet been reported. Point cloud based ITDs, however, have been applied to point cloud data generated from UAV photogrammetry, for example [54], who correctly identified 88.6% of trees in a ~37 ha of temperate deciduous forest in southwestern Pennsylvania, USA. However, UAV photogrammetry is restricted to relatively small areas which limits its application for large-scale operational forest inventories. Forest managers are continuously looking for affordable solutions to improve resource assessment at relatively large operational scales. For example, Pinus radiata plantations in Australia and New Zealand are of commercial importance, covering over 2.3 million hectares of the 4.2 million hectares worldwide [55], which require affordable and efficient methods to assess this resource over a typical 30-year rotation period.

Although raster-based ITD approaches are faster than point cloud based ITDs and can be directly applied to CHMs derived from DAP-based point clouds using existing methods [56], there is a need to investigate the application of point cloud based ITD approaches to large-scale DAP-based point clouds. If it can be shown that point cloud based ITD algorithms can be reliably applied to DAP-based point clouds, then this will provide additional evidence to support the utility of DAP and SfM photogrammetry as an alternative source of point cloud data for forest inventory.

The objective of this study was to evaluate the suitability of DAP-based point clouds for individual tree detection using point cloud based ITD methods in the case of a relatively homogeneous Pinus radiata plantation. The study investigated DAP-based point cloud datasets, acquired using two different cameras mounted on a small, manned aircraft, and an ALS dataset as input data types for ITD algorithms.

2. Materials and Methods

2.1. Study Area

The study area, a commercial Pinus radiata plantation located in north-east Tasmania, covers a region of approximately 2800 ha (Figure 1). The estate is managed by Timberlands Pacific Pty Ltd. The study area is stratified into three age classes: Early Age Inventory (EAI) aged 10–12 years, Mid Rotation Inventory (MRI) aged 20–22 years, and Pre-Harvest Inventory (PHI) aged 29–30 years. At the time of planting, the P. radiata seedlings were spaced at 3 m × 3 m with a stocking rate of about 1100 trees per hectare (TPH). The residual stocking, after initial thinning between 12–16 years, is 500 to 600 TPH. The MRI coupes then received a second thinning leaving a final stocking between 350–450 TPH. Broadleaf weed tree species are sporadically distributed throughout the plantation. Only PHI and MRI age class received silvicultural treatments such as thinning and weeding.

2.2. Data

2.2.1. Field Data

A total of 105 fixed-radius plots were distributed in the three age classes: 50 in PHI, 40 in MRI, and 15 in EAI. Plot diameters of the PHI, MRI, and EAI plots were 12 m, 9 m, and 8 m, respectively. These diameters of the PHI, MRI, and EAI plots were selected to account for differences in mean stocking rates among the age classes. Field data were collected in May 2015. Plot-centres were located in the field using a differential global navigation satellite system (GNSS). In each plot, the diameter at breast height (DBH) of all live standing trees (DBH ≥ 8 cm) and the height of at least 5 trees representing the range of heights per plot were recorded. Tree locations were not recorded in the field.

Thirty-six reflective targets (each 25 × 25 cm) were established across the study area. These targets were placed at the locations where there was a clear sky view, to ensure reliable GNSS fixes and to ensure their visibility in multiple overlapping photographs. The targets, fixed to ground pegs and geo-located using differential GNSS, were used as geospatial control for both small- and medium-format photography.

2.2.2. Remote Sensing Data

• Airborne Laser Scanning

Airborne laser scanning (ALS) was acquired on 12 April 2015. A fixed-wing aircraft was flown at a mean height of 1100 m above terrain. The ALS instrument onboard was an Optech Pegasus, which recorded 4 returns per pulse (1st, 2nd, 3rd and last). The pulse repetition frequency was 100 kHz, resulting in a mean point density and spacing of 1.94 m⁻² and 0.72 m, respectively. The horizontal and vertical accuracies achieved (within 1σ) were 0.55 m and 0.15 m, respectively. ALS data were vertically adjusted by the data provider using approximately 150 terrain calibration points. These terrain points, geo-located with real-time kinematic (RTK) positioning, were collected at three well-distributed locations in open and generally flat terrain. The data were classified by the data provider into ground and non-ground points.

• Digital Aerial Photogrammetry (DAP)

Medium format photography (MFP) was captured, simultaneously with the ALS data acquisition using a PhaseOne 65+ (60.5 megapixels) full-frame medium-format digital-back camera. The aircraft was flown at a mean height of 1100 m above terrain. The focal length of the camera was 51 mm, resulting in a ground sampling distance (GSD) of 0.125 m. A total of 859 images were captured over the study area with a forward- and side-overlap of 80% and 30%, respectively.

Small format photography (SFP) was captured using a Canon EOS 5D Mark II (21 megapixels) digital frame camera onboard a fixed-wing Cessna 206. The aircraft was flown at a mean height of 600 m above terrain on 6 February 2015. The focal length of the camera was 35 mm, resulting in a GSD of 0.13 m. A total of 1898 images were captured over the study area with a forward- and side-overlap of 75% and 60%, respectively.

3. Methodology

3.1. SFP and MFP Point Cloud Generation

Point cloud data were generated from SFP and MFP using Agisoft Photoscan Professional (v1.2.6, build 2834) and using the default settings available in the software package (see Iqbal et al. [45]) for a detailed description of these point cloud data). The resulting mean point density of the SFP and MFP point clouds was 28 and 22 points m⁻², respectively. Errors on GCPs during initial alignment were less than 0.07 m, 0.07 m and 0.05 m in easting, northing, and height, respectively.

3.2. Data Preparation

For this study, 52 plots (33 PHI and 19 MRI) were selected for analysis. Plots that were known to have a significant number of weed species, primarily wattle (Acacia dealbata), dogwood (Pomaderris aptala), and stink bush (Zieria arborescens), based on field notes and visual inspection of orthophotos, were excluded. The EAI age class was excluded from our analysis for three reasons: a high prevalence of weed species; because the focus of our work is on inventory estimation rather than early establishment counts; and because the application of ITD to small trees can be expected to behave differently from its application to more mature stands [38]. For the remainder of the plots (n = 52), field data were used to compute basal area and trees per hectare for each plot (summarised in

Table 1. Summary statistics of field data and their derived metrics for the selected MRI and PHI plots.

	MRI				PHI
	DBH (cm)	TH	TPH	BA	DBH (cm)	TH	TPH	BA
Min	20.11	22.83	440.00	51.50	28.02	26.37	177.78	29.03
Max	41.61	35.02	2120.00	82.92	57.53	38.84	568.18	69.95
Mean	31.22	30.80	1006.11	68.82	43.33	33.38	355.51	50.42
Std dev	6.12	2.86	437.45	9.18	6.20	2.61	100.48	10.47

; for details see Section 3.3 and

Table 2. Plot metrics computed from field and point cloud data. Metrics considered as field-based metrics are marked with an asterisk.

Plot Metric	Description	Plot Metric	Description
BA *	Basal area per hectare (m ha−1)	p10	10th percentile height
TH *	Top height for 5 trees/plot (m)	b10	% points between height cut-off and 10% of maximum height
TPH *	Number of trees per hectare	b20	% points between height cut-off and 20% of maximum height
cov5 *	ALS-based canopy cover above 5 m	b30	% points between height cut-off and 30% of maximum height
vci_als *	ALS-based vertical complexity index [60]	b60	% points between height cut-off and 60% of maximum height
rumple	An index of canopy surface roughness, calculated as the ratio between the canopy outer surface area and its projected area on ground [61]	b80	% points between height cut-off and 80% of maximum height
min	Height of lowest point (m)	b90	% points between height cut-off and 90% of maximum height
avg	Average height of points in a plot (m)	b99	% points between height cut-off and 99% of maximum height
std	Height standard deviation	d01	Point density between 5 m and 10 m (%)
ske	Skewness of height distribution	d02	Point density between 10 m and 20 m (%)
p01	1st percentile height	d03	Point density between 20 m and 30 m (%)
p05	5th percentile height	d04	Point density between 30 m and 50 m (%)

).

Point clouds data for the selected field plots were extracted using the field plot radii plus an external buffer of 2 m. To remove the effect of the underlying terrain, ALS points classified as ‘ground’ were used to compute the height of each point in the point cloud datasets relative to the ground—a process commonly known as ‘normalising’ point clouds. These point cloud data were then filtered: points with normalised height less than −0.5 m or greater than 50 m were classified as noise points and removed from further analysis. Figure 2c shows the vertical distribution of ALS, SFP, and MFP point clouds in 52 field plots, classified into 2 m height bins. Compared with SFP and MFP, ALS has the highest percentage of points that penetrated through the canopy. Compared with MFP, the percentage of SFP points is higher in the lower height bins (0–24 m) (see Iqbal et al. [45] for details on the behaviour of point clouds with respect to forest type).

3.3. Plot Metrics

For each plot, a total of 44 metrics were calculated. Six were derived from field measurements; 38 were derived from point cloud measurements. Field-based metrics were computed from field data using the Yield Table Generator (YTGen) software package (Simeltra, Takoroa, New Zealand). For each of the field plots, basal area (BA), top height (TH), number of trees per hectare (TPH), total stem volume (TSV), total recoverable volume (TRV), and quadratic mean diameter (QMD) were computed. Point cloud based metrics were calculated using LAStools [57] and lidR package in the R-software environment [58]. Plot metrics with a pairwise Pearson’s correlation greater than |0.8| were considered strongly correlated [59] and were removed from further analysis. The reduced set of plot metrics (n = 24) used in the correlation analysis is shown in Table 2. It is important to note that cov5 and vci_als were calculated for the ALS point cloud only. This means that these two-point cloud based metrics were not influenced by the DAP-based point cloud data and were only representative of vegetation structure. Hence, although calculated from a point cloud data, cov5 and vci_als were treated as field-based metrics in our analysis.

3.4. Reference Tree-Data

Reference tree-locations are crucial to measuring ITD-based tree detection accuracy. Tree-location data were not collected in the field due to a significant displacement between the base and tops of trees arising from stem lean and/or sweep and because of the unreliability of GNSS locations measured under dense canopies. As ITD algorithms detect treetops in a point cloud, determining their accuracy using reference data collected at ground-level was therefore complicated. For each of the 52 plots, we created reference tree-location data by visually examining an overlay of ALS, SFP, and MFP point cloud data. Treetops were digitised in CloudCompare, an open-source 3D point cloud and mesh processing software tool [62], and are referred to here as ‘reference trees’. First, all trees in each plot were marked in stereo-mode (using red-cyan glasses); second, the process was repeated (by the same operator) to identify any errors in the first round of marking; third, any discrepancies between the first and second round of identification were examined carefully and resolved. A total of 965 reference trees were identified in 52 field plots. An example of reference trees manually marked in a combination of point cloud data is shown in Figure 3. The total number of field-measured trees in these 52 plots was 991. A sample plot level comparison of the number of stems recorded in the field with the number of reference trees manually identified from point clouds resulted in a correlation of 0.93 (RMSE = 3.46), which indicated that it was reasonable to use the manually identified trees as a reference.

3.5. ITD Algorithms

For this study, we selected two point cloud based ITD algorithms viz. PointcloudITD [37,63] and Li2012 [64]. Parameterisation is required for both PointcloudITD and Li2012 before applying these algorithms to tree detection. These parameters were determined by trial-and-error, to determine an appropriate balance between correct detection and commission rates given that, for example, high detection accuracy can be achieved at the cost of high commission errors [38].

3.5.1. PointcloudITD

PointcloudITD (PCITD) was developed by Kathuria et al. [37] and extended by Bryson [63] to increase its computational efficiency, to include a machine learning component, and to improve usability with a graphical user interface. The application of this improved version is introduced in this current research. PCITD requires reference tree-locations in addition to other parameters. First, the algorithm identifies candidate treetops and then classifies these as tree-crowns based on reference tree-locations and focal statistics of the candidate treetops. A support vector machine (SVM)-based model is used for crown classification. Reference tree-locations are divided into training and validation samples for model building and accuracy assessment, respectively (see Kathuria et al. [37] for details). For the current study, 70% of reference tree-data was used for model building, reserving the remaining 30% for accuracy assessment. A software tool, freely available from [65], was used to apply PCITD to each of the three point cloud datasets.

3.5.2. Li2012

Li2012, originally developed by Li et al. [64], utilises horizontal spacing and height thresholds to iteratively classify each point in the point cloud by assigning tree IDs. Horizontal spacing thresholds adapt to the height of the point that is classified. Trees are segmented individually and sequentially, starting from the tallest tree to the shortest. First, the algorithm uses a local maximum filter to detect the highest point, a candidate top of an individual tree, in the normalised point cloud. Second, this target tree is then grown by including nearby points based on adaptive horizontal spacing thresholds and is removed from the point cloud once the target tree is completely segmented. Third, the algorithm continues to search for the next highest point in the remaining point cloud to segment a new tree. The process continues until all points are classified/clustered into trees (see Li et al. [64] for details). A minimum height threshold (5 m in our case) can be applied to exclude points below a certain height. An R-package (lidR) [58] was used to apply Li2012 to each of the three point cloud datasets.

3.6. Tree Detection Accuracy

Tree detection accuracy was assessed after identifying treetops in each of the ALS, SFP, and MFP point clouds using PCITD and Li2012. True positives (TP), false positives (FP), and false negatives (FN) were computed for all 52 plots. A TP is a tree identified by the algorithm and within 1.5 m of a reference tree; an FP is a tree identified by the algorithm but with no reference tree within 1.5 m (an error of commission), and an FN is when the algorithm fails to identify a tree within 1.5 m of a reference tree (an error of omission). A threshold of 1.5 m was selected based on field knowledge and was later checked in CloudCompare by measuring crown diameters for a mix of trees from MRI and PHI plots. It is acknowledged that this threshold may vary for tree species in different environments and conditions. Tree detection accuracy was also evaluated by computing recall (r), precision (p), and F-score [64,66], with each of these ranging from 0–1 (Equations (1)–(3)), where r and p are inversely proportional to errors of omission and commission, respectively. A high F-score, which is the harmonic mean of r and p, indicates the high overall accuracy of tree detection. Hereafter the r, p, and F-scores combined are referred to as tree detection rates.

$$r=\frac{TP}{\left(TP+FN\right)}$$

(1)

$$p=\frac{TP}{\left(TP+FP\right)}$$

(2)

$$F-score=2\times \frac{\left(r\times p\right)}{\left(r+p\right)}$$

(3)

Additionally, the relationships between tree detection rates and plot metrics were investigated by examining correlations between r, p, and F-scores and plot metrics (Table 2). In this paper, an uppercase ‘R’ is used to denote correlation and a lowercase ‘r’ for recall in order to differentiate between the two.

4. Results

4.1. Comparison of Individual Tree Detection Algorithms

Figure 4 compares the performance of the PCITD and Li2012 algorithms in terms of the proportion of detected trees (Figure 4a), errors of omission (Figure 4b), and commission (Figure 4c). The overall number of detected trees is evaluated with respect to the number of (manually identified) reference trees in all 52 plots. Errors of omission and commission were evaluated with respect to the number of reference trees and the total number of trees detected by the algorithm. All evaluations are presented in percentages. In Figure 4a, a detection percentage of 100 means that the number of trees detected by the algorithm, inclusive of commission errors, matched the number of reference trees. An overall detection percentage lower than 100 means that the algorithm identified fewer trees than the number of reference trees (a net deficit due to omission errors); whereas a percentage higher than 100 means that the algorithm identified more trees than the number of reference trees (a net excess due to commission errors).

Overall, Figure 4a shows that for our data PCITD tended to underestimate the number of reference trees in the ALS and MFP data, but slightly overestimate the number of reference trees in the SFP data. In contrast, Li2012 consistently overestimated the number of reference trees in all the three datasets, with the highest overestimation in ALS (approx. 38%).

Figure 4b shows the proportion of the reference trees that were detected (TP_r) by the algorithm and the proportion that was omitted (FN), and so the sum of detected and omitted trees is always 100%. Both algorithms were able to correctly detect more than 70% of the reference trees in all three datasets. In the case of ALS, Li2012 performed more reliably than PCITD: the percentage of correctly detected trees for Li2012 was ~13% higher than that of PCITD. In the case of SFP and MFP, the performance of the algorithms was comparable as indicated by the difference between the percentage of correctly detected trees which was always less than 5%. Across all the datasets, PCITD had a slightly smaller range of errors of omission (~8.7%) than that of Li2012 (~10.6%).

Figure 4c shows the proportion of the detected trees that could be matched with a reference tree (TP_d) and the proportion of detected trees that could not be matched with a reference tree i.e., False Positives and so errors of commission. The sum of matched and unmatched trees is always 100%. At least 60% of the trees detected by either of the algorithms matched the reference trees. Across all the three datasets, PCITD clearly outperformed Li2012: at least 77% of the trees detected by PCITD matched the reference trees, whereas at most 69% of the trees detected by Li2012 matched the reference trees. This also shows that while PCITD tended to underestimate the total number of reference trees (Figure 4a), it resulted in lower errors of commission compared with Li2012. Across all the datasets, the errors of commission were consistently lower for PCITD than they were for Li2012. Similar to our observation in Figure 4b, across all the datasets, the range of errors of commission of PCITD was about 7% lower than that of Li2010 (Figure 4c).

Generally, other research suggests that ITD algorithms tend to achieve a high percentage of correctly detected trees at the cost of high commission errors [38]. This means that commission errors are positively correlated with the proportion of correct detection (TP_r), which in our case was true for both PCITD and Li2012: for PCITD, the correlation between TP_r and commission errors calculated for each of the 52 field plots was 0.17, -0.01 and 0.2 for ALS, SFP, and MFP, respectively; whereas, for Li2012 the correlations between TP_r and commission errors were slightly higher than those for PCITD, i.e., 0.35, 0.56, 0.40 for ALS, SFP, and MFP, respectively. This indicates that, compared with Li2012, PCITD tended to achieve higher correct detections (accuracy) and lower commission errors.

4.2. Analysis of Tree Detection Rates with Respect to Canopy Structure and Point Clouds

For each of the 52 individual plots, tree detection accuracy of the two ITD algorithms were also calculated in terms of r, p, and F-score for each of the three point cloud datasets (Figure 5). Examining the performance of the two ITD algorithms for each of the datasets, two observations emerge. First, the values of r in the MRI plots are lower than those in the PHI plots, indicating higher errors of omission in the younger aged MRI plots compared with PHI plots. Second, the values of p in the MRI plots are higher than those in the PHI plots, indicating lower errors of commission in the MRI plots compared with PHI plots. Stocking rates in the MRI and PHI age classes were between 500–600 and 350–450 TPH, respectively and so a likely cause of these systematic findings may be stocking rate and consequent structural complexity of the canopy [64,67].

Comparative performance of ALS, SFP, and MFP is shown in

Table 3. Tree detection rates from PCITD and Li2012. These calculations are based on the total number of TP, FP, and FN in all 52 plots and for each of the ALS, SFP, and MFP dataset. The highest values of r, p, and F-score among the three datasets are highlighted in bold.

	PCITD			Li2012
	ALS	SFP	MFP	ALS	SFP	MFP
r	0.70	0.79	0.71	0.84	0.75	0.73
P	0.78	0.79	0.77	0.61	0.69	0.66
F-score	0.74	0.79	0.74	0.70	0.72	0.69

. The values of r, p, and F-scores are based on the total number of TP, FP, and FN in 52 plots. For PCITD, the performance of SFP is clearly better than that of ALS and MFP. Also, in the case of SFP, the errors of omission and commission are the same. This indicates that, compared with ALS and MFP, SFP achieved high tree detection accuracy and lower errors of commission. Tree detection accuracy of MFP was only slightly higher than that of ALS, however, the errors of commission for MFP were slightly higher than that for ALS. Overall, the three datasets achieved similar accuracy when PCITD was used: the maximum difference among ALS-, SFP- and MFP-based tree detection rates was extremely small (Δr, Δp, and ΔF-score were 0.09, 0.02, and 0.05, respectively).

For Li2012, the highest tree detection accuracy among the three datasets was achieved by ALS, however, the errors of commission for ALS were also the highest among the three datasets (Table 3). Compared with ALS, the SFP- and MFP-based tree detection accuracy and the errors of commission were both lower. Our results show that the performance of SFP was better than that of MFP. Overall, the three datasets responded differently to Li2012, with small differences among ALS-, SFP-, and MFP-based tree detection rates (Δr, Δp, and ΔF-score were 0.11, 0.08, and 0.03, respectively). Small differences among the ALS-, SFP-, and MFP-based tree detection rates from the two ITD algorithms suggest that the three datasets tended to achieve similar levels of accuracy.

4.3. Relationship between Plot Metrics and Tree Detection Rates

To investigate possible relationships between canopy structure and the tree detection rates (r, p, and F-score) for the three datasets, we computed Pearson’s coefficient of correlation between tree detection rates and the reduced set of plot metrics (Table 2). While overall these correlations tended to show similar trends across the three datasets, some notable differences were observed and are highlighted in

Table 4. Correlations between tree detection rates and plot metrics are given. Plot metrics that adversely affected detection rates are indicated by a negative sign. Correlations higher than |0.5| are given in bold.

ITD Method	Plot Metric	r			p			F-Score
		ALS	SFP	MFP	ALS	SFP	MFP	ALS	SFP	MFP
PCITD	BA	−0.45	−0.30	−0.28	0.45	0.40	0.54	−0.12	0.08	0.17
	TPH	−0.66	−0.39	−0.40	0.66	0.48	0.72	−0.23	0.06	0.16
	cov5	−0.44	−0.22	−0.09	0.49	0.19	0.63	−0.06	−0.04	0.39
Li2012	BA	−0.40	−0.53	−0.48	0.56	0.58	0.61	0.41	0.07	0.21
	TPH	−0.62	−0.76	−0.71	0.83	0.83	0.81	0.54	0.03	0.15
	cov5	−0.41	−0.53	−0.39	0.71	0.72	0.79	0.61	0.30	0.51
	rumple	−0.17	0.61	0.22	0.22	−0.51	−0.62	0.22	0.07	−0.41
	min	−0.32	−0.50	−0.28	0.40	0.58	0.62	0.25	0.11	0.40
	std	0.34	0.43	0.18	−0.47	−0.63	−0.58	−0.33	−0.24	−0.38
	ske	0.12	−0.40	−0.16	−0.13	0.52	0.39	0.01	0.18	0.25
	p01	−0.17	−0.35	−0.07	0.22	0.53	0.47	0.20	0.21	0.38
	b80	0.39	0.45	0.30	−0.41	−0.45	−0.63	−0.24	−0.06	−0.36

.

For both ITD algorithms, plot metrics with a correlation higher than |0.5| with at least one of the tree detection rates in any of the three datasets are summarised in Table 4. Correlations higher than |0.5| are highlighted in bold. Correlations lower than or equal to |0.5| were considered relatively weak; therefore, plot metrics with correlations lower than or equal to |0.5| with tree detection rates for all the three datasets are not presented in Table 4. Overall, a typical relationship between the values of r and p can be observed: tree detection accuracy increases at the cost of increase in errors of commission and vice-versa.

Table 4 shows that, compared with Li2012, fewer plot metrics (n = 3) had an influence on the PCITD-based tree detection rates. For PCITD, there was no consistent trend observed across the three datasets. Among all the three datasets, the ALS-based value of r was strongly negatively influenced by TPH (R = −0.66), meaning that tree detection accuracy decreases with an increase in stocking. Compared with the ALS-based value of r, the lower correlation of SFP- and MFP-based values of r with plot metrics suggest that plot metrics have a lesser influence on tree detection accuracy for SFP and MFP when PCITD was used. Among the three datasets, the influence of plot metrics is the lowest on SFP-based values of p. A strong positive correlation (R = 0.66) between the ALS-based p value and TPH suggests that errors of commission decrease with an increase in stocking when ALS data is used. In the case of MFP, our results show that errors of commission decrease with an increase in BA, TPH, and cov5. Regarding the overall accuracy of tree detection, the F-score did not show a strong correlation with any of the plot metrics. Our PCITD-based results probably suggest that this algorithm is relatively less sensitive to plot metrics.

Compared with PCITD, Li2012-based tree detection rates were sensitive to many plot metrics (Table 4). A consistent trend was observed across the three datasets: the values of r were negatively influenced by TPH, i.e., an increase in stocking resulted in a decreased value of r (meaning high rates of omission). In comparison with SFP and MFP, the influence of TPH was lower on the ALS-based value of r (correlation between r and TPH for ALS, SFP, and MFP was −0.62, −0.76, and −0.71, respectively). This suggests that compared with SFP, and MFP, ALS-based tree detection accuracy is influenced to a lesser extent by TPH when Li2012 is used.

In all three datasets, the values of p were favoured by increasing BA, TPH, and cov5 as indicated, respectively, by positive correlations of 0.56, 0.83, and 0.71 for ALS; 0.58, 0.83, and 0.72 for SFP; and 0.61, 0.81, and 0.79 for MFP. Among BA, TPH, and cov5, the correlation between TPH and the value of p for each of the datasets was the strongest. For all three datasets, the correlations among the values of p and BA, TPH, and cov5 were similar. This suggests that with an increase in BA, TPH, and cov5, errors of commission for the three datasets follow a similar decreasing trend.

SFP-based values of r were favoured by an increase in rumple (R = 0.61), which indicates that the higher the canopy surface roughness the lower are the errors of omission. BA and cov5 are shown to adversely affect r (R = −0.53 and −0.53, respectively); i.e., an increase in BA and cov5 resulted in higher rates of omission. In all three datasets, the value of r did not have a strong correlation with any other plot metric.

In addition to BA, TPH, and cov5, the plot metric that favoured SFP- and MFP-based values of p was min (R = 0.58 and 0.62, respectively); however, the influence of min on SFP is slightly lower than on MFP. This is probably due to the higher penetrative ability of SFP compared with MFP as illustrated in Figure 2c. Both SFP- and MFP-based values of p were adversely affected by rumple (R = −0.51 and −0.62) and std (R = −0.63 and −0.58, respectively). This presents a typical case, as observed above, that an increase in surface roughness favours tree detection accuracy (the value of r) at the cost of errors of commission. SFP-based values of p were favoured by ske and p01 (R = 0.52 and 0.53, respectively). In addition to those mentioned above, the MFP-based value of p increased with decreasing b80 (R = −0.63).

F-score responded differently to each of the datasets: an increase in TPH and cov5 favoured ALS-based overall accuracy (R = 0.54 and 0.61, respectively); whereas, MFP-based overall accuracy increased with an increasing cov5 (R = 0.51).

5. Discussion

In this study, we evaluated the suitability of SFP- and MFP-based point clouds for detecting individual trees in comparison with ALS data for a P. radiata plantation in north-east Tasmania. Our findings indicate that ITD algorithms can be applied to SFP- and MFP-based point clouds with results comparable to that from an ALS point cloud. They also suggest that the proportion of correctly identified trees is influenced by factors that include the choice of ITD algorithm, the canopy structure, and the response of point cloud data to the structural elements of the canopy.

5.1. Individual Tree Detection Algorithms

The accuracy levels achieved by the two ITD algorithms, particularly in terms of true positive (TP), false positive (FP), and false negative (FN) results, were not consistently similar (Figure 4). Overall, a comparison of the two ITD algorithms showed that for our data the performance of PCITD was better than that of Li2012. As noted in Section 4.1, PCITD tended to achieve higher detection accuracies and lower commission errors in comparison with Li2012. We attribute this to the different architecture of the two algorithms. PCITD draws its strength from training data (i.e., reference tree-locations) to build a classification model and classify the point cloud data to identify trees/crowns. Li2012 is solely based on point cloud data, uses horizontal distance and height thresholds, and classifies each point in the point cloud by assigning it to a tree. For our data, Li2012 was more prone to commission errors than PCITD. We note two possible explanations for these higher commission errors. First, parameterisation has a significant effect on the resultant tree detection accuracies. A smaller horizontal distance threshold may improve the percentage of correctly detected trees but at the cost of an increase in commission errors. Similarly, a larger horizontal distance threshold may reduce commission errors but at the cost of increase in omission errors. These parameters need to be tuned to the forest structure based on the knowledge of the study area. Second, as noted in Li et al. [64], misclassification may occur when the canopy is not uniformly sampled due to low ALS point density. This might have affected our Li2012-based results as the average ALS point density was ~2 points m⁻². The SFP- and MFP-point clouds suffer from occlusion which may result in the unequal sampling of the canopy. When using Li2012, it is anticipated that tree detection accuracy may improve with an increased ALS point density and with effective flight planning that minimises the effects of occlusion and shadowing, with respect to DAP-based point clouds.

The better performance of PCITD may also be influenced by the fact that PCITD was primarily developed for P. radiata plantations whereas Li2012 was developed using a study area that was characterised by mixed conifer forest with a range of tree densities. The performance of ITD algorithms may be slightly better in the conditions for which they were developed [28]. A disadvantage of PCITD is its dependence on training data, which may not always be available.

It is noteworthy that TP, FP, and FN were calculated based on reference tree-data that was created by manually identifying trees in the point cloud datasets—an approach that has been used in several similar studies (e.g., [38,51,64]). The drawback of this approach is that the manual identification of reference trees from point cloud data requires interpretive skill and is unlikely to be exactly replicable. Potential solutions to this could be: (i) collecting geolocation data using GNSS for each tree in a field plot; (ii) having multiple operators employed to mark reference trees in the point cloud; and (iii) having the same operator repeating the marking process several times. The first two solutions have complications in their practical application as these require additional resources. The third option was employed in this study (as explained in Section 3.4). In this current research, the process was repeated for 52 plots, and it is likely that there was an improvement in the interpretive skill of the operator through the first run, which was then used to validate the process over the second run of the tree marking process. This has been shown by the high correlation (0.93) between the number of trees in field plots against that marked manually from the point clouds without referring to field counts during the marking process (~97% of the field trees were marked in the point clouds), indicating the suitability of manually generated reference data. Further, it must be noted that field-based measurements of treetop location are also difficult and generally lack precision. A recurring challenge in studies of this kind is that the remotely sensed data may provide greater accuracy than field observations.

5.2. Analysis of Tree Detection Rates with Respect to Canopy Structure and Point Clouds

Our results show that canopy structure has an influence on tree detection rates (Figure 5). In most cases, for both ITD algorithms, tree detection accuracy (the value of r) was relatively low in the MRI plots compared with the PHI plots. The value of p, in most cases, was relatively high in the MRI plots compared with the PHI plots. The relationship of the values of r and p with MRI and PHI plots can be explained by the different stocking rates between these plots, with stocking rate in the MRI plots higher than in the PHI plots. As reported in previous studies [38,64,67], errors of omission are relatively higher in dense plots than in sparse plots. Similarly, errors of commission are relatively lower in dense plots than in sparse plots. This can possibly be explained by the behaviour of the tree detection algorithm. ITD algorithms that use a search window for local maxima detection, as in our case, may result in high errors of omission if the size of the search window is bigger than the spacing between the treetops. For example, in relatively dense plots (such as MRI), it is possible that more than one reference/actual treetops will fall within the search window, out of which only the highest will be identified as a treetop by the algorithm. While in dense plots the errors of omission could be high, the likelihood of the detected treetops to be true positive is also high, which is shown by the higher values of p in the MRI plots than that in the PHI plots (Figure 5).

As noted in Section 4.1, tuning parameters in ITD algorithms significantly affect tree detection accuracies. It is expected that tree detection accuracy may improve if these parameters are tuned separately for each age class/stand in a plantation, particularly if training data (reference tree-data) are not available. ITD algorithms that use training data are expected to account for the variation in stocking rates among age classes/stands.

Comparing the three datasets, our results are encouraging-showing that tree detection rates for ALS, SFP, and MFP were largely similar irrespective of the ITD algorithm used: the difference among overall tree detection rates (52 plots combined) of the three point cloud datasets was always less than 0.11, 0.08, and 0.05 for r, p, and F-score, respectively (Table 3). ALS data penetrates deeper into the canopy (Figure 2c and is less affected than DAP by occlusions (e.g., [45]). This suggests that it is highly likely that ALS will detect trees that were not represented, in part or completely, by the DAP-based point clouds. Our results, however, show that in our study area (i.e., a P. radiata plantation) DAP resulted in tree detection rates similar to ALS. The similar performance of DAP and ALS in this type of forest can be attributed to relatively regular spacing and even height of plantations, and that the effects of occlusion and shadowing are minimal in the upper canopy (particularly where terrain slope is mild). This indicates the suitability of SFP- and MFP-based point clouds for individual tree detection in a single-layered P. radiata plantation. In multi-layered forests, the results may be different because DAP can be expected to miss smaller trees due to the lower penetrative ability of DAP compared with ALS.

Comparing the two DAP-based point clouds, irrespective of the algorithm used, the performance of SFP was slightly better than that of MFP; however, the difference between tree detection rates was very small. The difference between their respective values of r, p, and F-scores was less than 0.08, 0.03, and 0.05, respectively. Our results strongly suggest that forest managers may choose between SFP and MFP on the basis of operational considerations rather than the relative performance of the resultant point clouds for stocking estimates.

5.3. Relationship between Plot Metrics and Tree Detection Rates

PCITD showed that ALS-based tree detection accuracy (the value of r) and the errors of commission were strongly correlated with TPH only, and that MFP-based errors of commission-only were strongly correlated with BA, TPH, and cov5. For this ITD method, SFP-derived tree detection rates did not show any strong correlation with any of the plot metrics. In comparison with Li2012, the correlations between tree detection rates and plot metrics were weaker for PCITD in nearly all cases. In order to evaluate the relationship between plot metrics and the three point cloud datasets, in the section below we base our discussion on the Li2012 results.

Examining first the field-based plot metrics, our results indicate that tree detection accuracy (the values of r) was negatively correlated with stocking (trees per hectare) and basal area (Table 4). Plots with higher stocking rates and higher basal area were associated with higher errors of omission (more false negatives). We found that the correlation between tree detection accuracy and TPH was stronger than that between tree detection accuracy and BA. It can be inferred that omission errors were mainly driven by the stocking rates in our study area. High stocking rates lead to more overlapping crowns, particularly in even-aged forests, due to a decrease in spacing between treetops [67,68], which resulted in high omission errors (as explained in Section 5.1). This also means that while omission errors increase with an increase in stocking rates, commission errors tend to decrease because the algorithm is less likely to falsely detect a treetop when the stocking rate is high. This is indicated by the strong positive correlation of the value of p with BA, TPH, and cov5. As stocking rate and canopy cover are closely connected, the relationship of cov5 with errors of commission is similar to that of TPH. Previous studies have shown that errors of omission and commission counterbalance each other [64], which is shown by the relatively weak correlations of F-scores with TPH and BA. Among the three datasets, the ALS-based F-score showed the strongest correlation with TPH and cov5, which indicates that the overall tree detection accuracy for ALS improved with an increase in stocking rates. It is important to note that the response of ALS, SFP, and MFP point clouds to TPH, BA, and cov5 was comparable, particularly the values of r and p in Table 4.

Examining the point cloud based plot metrics, there are differences that can be explained by the characteristics of the ALS and DAP-based point clouds. Comparing the errors of omission and commission for each dataset (i.e., comparing ALS r with ALS p, SFP r with SFP p, and MFP r with MFP p), mostly these point cloud based metrics were more strongly correlated with commission errors than they were with omission errors (Table 4).

The value of p was negatively correlated with rumple for both of the DAP-based point clouds. This indicates that errors of commission increase with an increase in canopy outer surface roughness. An explanation for this observation may be that dense DAP-based point clouds tend to characterise the upper canopy surface in great detail, which may result in false peaks that are identified as trees by the algorithm. Another possibility may be the presence of noise points generated by the photogrammetry software and that may add to the roughness of the canopy surface and present as false treetops. Further, incomplete coverage of the canopy in DAP-based point clouds may result in high canopy outer surface roughness [64].

The value of p was positively correlated with the point cloud-metric min for both of the DAP-based point clouds. This indicates that errors of commission decrease with increased penetration through the canopy. This can be explained by the penetrative ability of the three point clouds, which is the highest for ALS, followed by SFP and MFP (Figure 2c). Comparing the relationship of ALS-, SFP- and MFP-based values of p with the min metric, it can be inferred that the relationship between p and min weakens as the penetration through the canopy increases. With high penetration through the canopy, there is a possibility that the (almost) complete morphological structure of large branches located at low heights will be registered in the DAP and the ITD algorithm will be able to associate these branches to an existing tree rather than falsely identifying them as individual treetops or separate trees.

The value of p was negatively correlated with std for both of the DAP-based point clouds. This indicates that errors of commission decrease when height-variation in the DAP-based point cloud are small. This suggests that the smaller the variations in the heights of DAP-based point clouds, the smoother can be the canopy outer surface (low rumple), which will decrease the errors of commission.

Comparing the F-scores of the three datasets, except TPH and cov5, the overall accuracy of tree detection was weakly correlated with plot metrics. Compared with SFP and MFP, the overall accuracy of ALS-based tree detection is favoured by an increase in canopy cover. Alternatively, it can also be suggested that increasing the ALS point density will result in more canopy hits, which may possibly increase the overall accuracy of tree detection [38].

It should be noted that we computed Pearson’s coefficient of correlation to investigate the relationship between tree detection rates and the reduced set of plot metrics. Pearson’s coefficient of correlation is highly sensitive to outliers and, hence, should be used with care. The data used for this analysis, according to Tukey’s rule [69], did not have extreme outliers.

6. Conclusions

Point cloud based individual tree detection algorithms developed for ALS data have, to our knowledge, not been applied to DAP-based point clouds. In this study, we applied point cloud based ITD algorithms to dense point clouds derived from small- and medium-format digital aerial photogrammetry acquired over a P. radiata plantation and compared our results with those from an ALS point cloud. Generally, there is a good agreement between ALS- and DAP-based results, suggesting the suitability of DAP-based point clouds for detecting individual trees. This also suggests that even though the architecture of the ITD algorithms was different, their performance in a homogeneous plantation appears to be comparable for ALS- and DAP-based point cloud data. It is acknowledged that this research was conducted in a managed conifer plantation, which provided a favourable environment for individual tree detection, particularly when field plots with weed species were excluded from the analysis. Nevertheless, the MRI and PHI plots included in our analysis had, as observed in the field, quite complex intersecting crowns. Our results show that in large part tree detection rates (r, p, and F-score) are strongly associated with the number of trees per hectare (TPH). Although previous research suggested that point cloud metrics derived from ALS- and DAP-based point clouds were significantly different [45], these differences did not show a strong influence on tree detection rates. Plot metrics derived from point cloud data were relatively weakly correlated with tree detection rates. These findings support the application of digital aerial photography and SfM-MVS photogrammetry as a practical alternative to ALS for plantation forest inventory, provided a terrain model of sufficient accuracy is available either from historic data or from a one-off LiDAR acquisition.