The Use of Satellite Data to Determine the Changes of Hydrodynamic Parameters in the Gulf of Gdańsk via EcoFish Model

Abstract

Using mathematical models alone to describe the changes in the parameters characterizing the analyzed reservoir may be insufficient due to the complexity of ocean circulation. One of the ways to improve the accuracy of models is to use data assimilation based on remote sensing methods. In this study, we tested the EcoFish numerical model that was developed for the Gulf of Gdańsk area, under the FindFish Knowledge Transfer Platform. In order to improve the model results and map local phenomena occurring in the studied water, which would be difficult to simulate using only mathematical equations, EcoFish was extended with a satellite data assimilation module that assimilates the sea surface temperature data from a medium-resolution imaging spectroradiometer and an advanced ultrahigh-resolution radiometer. EcoFish was then statistically validated, which resulted in high correlations for water temperature and salinity as well as low errors in comparison with in situ experimental data.

1. Introduction

The Baltic Sea is a shallow inland sea connected to the North Sea by narrow (4–28 km wide) straits. The topography of these straits, and in particular their low depth (around 5–6 m in most shallow points), impedes the free exchange of waters between the Baltic and the North Sea, causing significant water exchanges between these seas only during large infusions [1,2]. The Gulf of Gdańsk is the southern part of the Baltic Sea and is less affected by infusions, but it is exposed to influences from the land. The highly urbanized and industrialized coast has a huge impact on the environmental conditions of the Gulf in addition to the waters coming from the Vistula River [3,4]. An additional obstacle in the exchange of the Bay’s waters with the open sea is the Hel Peninsula. It serves as a natural land barrier, marking the border between the Puck Bay and the Gdańsk Basin.

The morphometric conditions of the Gulf of Gdańsk favor the heterogeneity in salinity. Visible differences can be observed between the shallow coastal area hydrologically belonging to the surface layer of the Baltic Sea and the remaining deeper zone of the gulf [5,6]. However, smaller differences exist between the deep water region of the Gulf of Gdańsk and the open sea, where a typical for the Baltic Sea, layered water structure can be observed [7].

Comprehensive understanding and description of processes occurring in water is possible through the combined use of mathematical models, modern in situ research, and observational techniques in the form of satellite remote sensing [8,9,10,11].

In order to increase the intensity of knowledge transfer and the use of scientific potential by fishermen, and consequently contribute to the sustainable development of fisheries while increasing the protection of the Gulf’s ecosystem, a three-dimensional, prognostic ecohydrodynamic model named EcoFish was built. The EcoFish model is configured for the Gulf of Gdańsk area and being developed under the project “FindFish Knowledge Transfer Platform—Numerical Forecasting System for the Marine Environment of the Gulf of Gdańsk for Fisheries” [12].The main goal of the project is to create a platform from which users (in particular fishermen and scientists) will be able to obtain knowledge and information about the physical and biological conditions of the Gulf of Gdańsk. The EcoFish model will be an essential tool in achieving this goal.

The most important modeled variables (especially water temperature, salinity, and dissolved oxygen concentration) that determine the state of the Gulf of Gdańsk ecosystem will also serve as input data for the Fish Module. Output information from this module, together with the data on fish preferences and expert knowledge, will allow the creation of maps of the most favorable environmental conditions for the occurrence of industrial pelagic fish in the Gulf of Gdańsk region, i.e., herring, sprat, and flounder.

The implementation of the satellite data assimilation module for sea surface temperature (SST), and also for chlorophyll a later in the biological part, in the EcoFish model will ensure that the obtained model results will be even more accurate (close to reality) and the model will correctly reflect the state of the Gulf of Gdańsk environment. In this study, the results from the EcoFish model were statistically validated.

2. Materials and Methods

2.1. Study Area

The domain of the EcoFish model includes the extended Gulf of Gdańsk (Figure 1), which is the southern part of the Gdańsk Deep area, located in the Gotland Basin. A straight line connecting Cape Rozewie with Cape Taran delimits the proper Gulf of Gdańsk. This line crosses the deepest parts of the Gdańsk Deep, with a maximum depth of 118 m. Along the coastal zone, there is a wide strip of shallows widening to the west of the mouth of the Vistula River. The slope of the bottom in the coastal zone is varied. The greatest decline occurs at the headland of the Hel Peninsula, where the bottom rapidly drops to a depth of 70 m [13].

The Bay of Puck is a shallow area of the Gulf of Gdańsk located in its western part [14,15]. Due to its geographical location and special hydrological conditions, the Bay of Puck is a reservoir unique in the scale of the entire Baltic Sea. It owes its specificity to natural factors: isolation from the sea waters by the Hel Peninsula and separation into two morphologically and environmentally different zones—the part known as outer Bay of Puck and the semienclosed, inner part called Puck Lagoon to the northwest.

2.2. EcoFish Model Configuration

EcoFish origins from Community Earth System Model (CESM) coupled global climate model http://www.cesm.ucar.edu/models/ccsm4.0, accessed on 1 June 2018 by NCAR. CESM is a state-of-the-art model system consisting of five separate components with an additional coupler controlling time, exciting forces, domains, grids, and information exchange between the models. For the purpose of the FindFish project, CESM was downscaled and adapted for the Gulf of Gdańsk region for further development at the Institute of Oceanology, Polish Academy of Sciences.

EcoFish’s horizontal resolution is 575 m (1/192°). The vertical resolution is 5 m for each layer with a total of 26 layers (

Table 1. EcoFish model vertical resolution.

Model Level	Thickness [m]	Low-Depth [m]	Mid-Depth [m]
1	5.0	5.0	2.5
2	5.0	10.0	7.5
3	5.0	15.0	12.5
4	5.0	20.0	17.5
5	5.0	25.0	22.5
6	5.0	30.0	27.5
7	5.0	35.0	32.5
8	5.0	40.0	37.5
9	5.0	45.0	42.5
10	5.0	50.0	47.5
11	5.0	55.0	52.5
12	5.0	60.0	57.5
13	5.0	65.0	62.5
14	5.0	70.0	67.5
15	5.0	75.0	72.5
16	5.0	80.0	77.5
17	5.0	85.0	82.5
18	5.0	90.0	87.5
19	5.0	95.0	92.5
20	5.0	100.0	97.5
21	5.0	105.0	102.5
22	5.0	110.0	107.5
23	5.0	115.0	112.5
24	5.0	120.0	117.5
25	5.0	125.0	122.5
26	5.0	130.0	127.5

). The vertical discretization uses the z formulation and the bottom topography is based on the Baltic Sea Bathymetric Database (BSBD) from the Baltic Sea Hydrographic Commission [16]. The bathymetric data were interpolated into the model grid using the Kriging method.

The EcoFish model consists of two active and two passive components. The active prognostic models are Parallel Ocean Program (POP) and Community Ice CodE (CICE). The passive components are responsible for providing atmospheric data fields and fresh water from catchment area. The main part of this system is the ocean model in which horizontal mixing is represented by biharmonic operator that is implemented by applying the Laplacian operator twice. It is performed in both viscosity and diffusion schemes; however, the mixing coefficients are different and equal to $-3\times {10}^{14}$ and $0.3\times {10}^{14}$, respectively (note: the sign was omitted). Vertical mixing used by authors in EcoFish system is called k-profile parametrization (KPP) [17]. Shear instability is parameterized in terms of the gradient Richardson number, while diffusivity (active tracers) and viscosity (momentum) are parameterized as diapycnal. Each active component has its own time step. The CICE time step is 10 min and it is equal to the coupling time step. Ocean model has typically two mods and time step is divided into two parts. The baroclinic part makes one step in 60 s. Because the model has linear free surface formulation, it is not needed to make substeps for the barotropic part. CESM is intended for use in global applications; thus, it was adapted for this purpose. Barotropic equation has been modified for possibility of assimilation of sea level at the boundaries [18]. Additionally, at the boundary area, salinity has been forced to have values from external model using restoring. The restoring time scale is not constant and depends on distance from the boundaries. Exactly at the boundaries, the restoring time scale is in the range of days and it increases to infinity toward the center of the domain at a distance of about 20 km (40 model cells). Similar models were already presented in [18,19].

2.3. Open Boundary

The results from the EcoFish model analyzed in this paper were spatially limited to the Gulf of Gdańsk area. However, the entire domain of the model is slightly larger and borders on the west and north with the open Baltic. Therefore, it is necessary to provide the model with boundary conditions. Apart from water temperature and salinity, it is necessary to prepare the data of sea surface height and barotropic components of sea currents. The data to the model boundary are provided by a 3D CEMBS [20,21] model with a horizontal resolution of 2 km. Since the exact determination of the data range on the border required trials with different settings, it was decided to prepare data on the entire FindFish domain, not only on its border. This allows the use of the same data regardless of the finally adopted settings. The fact that the results of the 3D CEMBS model are used as the source of boundary conditions means that 3D CEMBS’s calculations must be performed prior to EcoFish.

2.4. Atmosphere Forcing

At the water–atmosphere border, the EcoFish model is fed with meteorological forcing. These data come from the UM (Unified Model) developed at the Interdisciplinary Modeling Center of the University of Warsaw (ICM UW). Parameters directly used as inputs are as follow:

• 10 m wind speed,
• 2 m air temperature,
• specific humidity,
• sea level pressure,
• precipitation (convective and large-scale),
• downward shortwave and longwave radiation

Missing parameters are calculated by the atmospheric data module, which is an integral part of the EcoFish model. Air density and scattered and direct shortwave radiation in the visible and near-infrared range are determined that way.

2.5. River Discharge

Due to the fact that modeling of surface runoff requires the use of a hydrological model, The Soil & Water Assessment Tool (SWAT) software was used [22,23,24]. SWAT is a small watershed to river basin-scale model used to simulate the quality and quantity of surface and ground water and predict the environmental impact of land use, land management practices, and climate change. This adaptation of SWAT was developed under the WaterPUCK—Integrated Information and Prediction Service project [11]. Meteorological data (precipitation, wind, temperature, and atmospheric pressure) comprise a key element of any water balance model. The SWAT hydrological model is based on real-time observations (local meteorological station) as well as shorter weather forecasts (ICM UW website). The conversion of rainfall data into surface runoff is accomplished using the SCS (Soil Conservation Service) Curve Number procedure through the cumulative runoff volume and concentration time. SWAT covers sedimentation in surface and groundwater, and the transport model also includes snow cover. Additionally, the transport of nutrients and pesticides was taken into account for use at a later stage related to the launch of the biochemical part of the EcoFish model.

The SWAT model was created for six rivers (numbered 8–13) from the described domain (

Table 2. Rivers mouths’ locations included within the EcoFish model domain and mean runoff.

	Source	River	Longitude	Latitude	Mean Runoff [m${}^3$/s]
1	HYPE	Vistula	18.95	54.35	1064
2	HYPE	Bold Vistula	18.78	54.37	2.05
3	HYPE	Still Vistula	18.66	54.41	6.06
4	HYPE	Oliwski Stream	18.60	54.42	0.31
5	HYPE	Kamienny Stream	18.56	54.46	0.45
6	HYPE	Kacza	18.56	54.48	0.29
7	HYPE	Ściekowy Canal	18.51	54.61	0.21
8	SWAT	Zagórska Stream	18.47	54.63	0.11
9	SWAT	Reda	18.47	54.64	0.48
10	SWAT	Mrzezino Canal	18.46	54.66	0.20
11	SWAT	Gizdepka	18.46	54.66	0.30
12	SWAT	Żelistrzewo Canal	18.45	54.70	0.17
13	SWAT	Płutnica	18.39	54.72	0.91

). For the remaining seven rivers (numbered 1–7), information on the runoff volume was taken from the Hydrological Predictions for the Environment (HYPE) model. It is a physics-based semidispersed catchment model that simulates the flow of water and substances as they travel from precipitation to discharge into the sea. We used historical time series from 1980–2010 for the geographic domain of Europe available as daily averages. Spatial resolution is determined by dividing the land area into catchments for which the HYPE data represent mean values at the estuary. The volumes for the years 2014 to 2020 have been calculated as the multiyear average over the available 30-year period.

2.6. Simulation Run

The EcoFish model was validated using the results of a seven-year simulation from 1 January 2014 to 31 December 2020, preceded by a two-year model spin-up. This run was calculated using the above-described model configuration with satellite data assimilation for surface temperature. Results were recorded four times a day as 6-h averages. The simulation results and model validation are presented in Section 4.

Additionally, in order to verify the correctness of the assimilation module itself, the same simulation was carried out without the assimilation of satellite data for the surface temperature. Both runs were then compared against satellite data.

2.7. Data Sets Used for Evaluation

Two in situ databases were used for the statistical analysis of the EcoFish model. Detailed descriptions are provided below.

2.7.1. ICES

The main in situ database that was used to validate the water temperature and salinity in the EcoFish model is the hydrochemical database provided online by the International Council for the Exploration of the Sea (ICES) via the https://ocean.ices.dk/HydChem/, accessed on 1 Febuary 2021 website. 17,902 measurements from 2014 to 2019 were used for comparison. Data for 2020 was not yet available in the database at the day of this validation. Most of the data was from 2014 (6130 measurements) and 2015 (6848 measurements). From 2016 to 2019, 1055 to 1444 measurements per year were available. ICES measurements covered almost the entire domain (Figure 2), except its eastern part, which covers areas along the Vistula Spit to the easterly coast of Gulf of Gdańsk. The region with the densest measurement grid was the strip along the 19°E meridian.

ICES measurements were relatively uniformly distributed throughout the water column. In the surface layer from 0 to 5 m, 1082 measurements were available, in the layer from 5 to 30 m—5429, in the layer from 30 to 80 m—8987 and 2404 measurements for depths greater than 80 m.

2.7.2. Fishing Cruises

We had an additional database that was used to validate the model. It was a set of measurements taken under the FindFish project during fishing cruises. Valeport MIDAS CTD model 500 and GPS 73 Worldwide by GARMIN were used for this purpose. Recording of physicochemical data was carried out during fishing with towed and set gears. The following parameters were saved in the device memory:

• water temperature,
• salinity,
• pressure,
• turbidity,
• saturation,
• pH.

Data from the MIDAS CTD instrument were collected in the area north of the Vistula River mouth and in the strip in the open sea, parallel to the Hel Peninsula (Figure 2). The measurements have a high temporal and spatial resolution. Therefore, they were averaged to match the model mesh. After this operation, we had 15,312 records. The highest density of measurements (8533 values) were from 30 to 60 m deep layer. It was closely related to the optimal fishing depth. The first data was collected on 22 May 2018 during pelagic fishing. To date, 422 hauls/releases have been made, of which 306 were harvested with towed gear and 116 with set gear. Most of the data was collected in 2020 (7293 measurements) and 2019 (5954 measurements). The remaining 2065 measurements were taken in 2018. The months with the highest amount of data collected were April (3150) and March (2395). Measurements were taken from the decks of 10 vessels, and the schedule of their cruises was determined on an ongoing basis in relation to the frequency of occurrence of fish species being the target of the catch. In addition, meteorological data were also recorded, including air temperature, wind strength and direction, cloud cover, and sea state, which were collected in the form of questionnaires completed by skippers.

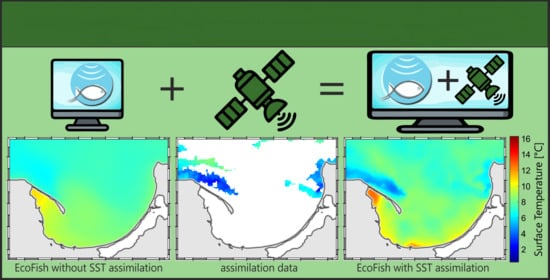
3. Assimilation of Satellite Data in the EcoFish Model

3.1. Satellite Data Acquisition and Processing Module

The satellite sea surface temperature data (SST) used along with EcoFish model come from the SatBałtyk project database [8,9] and are based on measurements from a medium-resolution imaging spectroradiometer (MODIS AQUA) and an advanced ultrahigh-resolution radiometer (AVHRR). These data are calibrated to local conditions in the Baltic region and subjected to atmospheric correction and filtration. Raw maps are linked in space, geometrically corrected for changes in satellite position, and radiometrically corrected in case of numerical errors in data transmission. Data in the SatBałtyk system have a horizontal resolution of 1 km and cover the entire area of the Baltic Sea. Daily average values obtained from the combination of all satellite images available on a given day are used for assimilation. Assimilation takes place during the assimilation window with the peak of the window set to 12:00. This is taken into the account during the process of combining data using weighted averaging. The data acquisition management module automatically detects the presence of new data, downloads new files to a local storage, processes the data, and saves the result together with control files and metadata. Data processing consists of their interpolation onto the 575 m grid of EcoFish model and saving in the file format compliant with the model requirements. Thanks to the aforementioned control files, the module managing the entire system can monitor the status of satellite data on an ongoing basis and, if available, start assimilation.

3.2. Satellite Data Assimilation Module

The assimilation module is based on modified and extended CESM model [25,26] components that are an integral part of the EcoFish model. This allowed for smooth introduction of satellite information to computed data with each time step. In addition, it allowed the reuse of a number of settings and functionalities already available in the CESM, e.g., parameterization of the length of the assimilation window currently set to 24 h, the frequency of assimilation (each time step) and the modules for reading and processing data by the model. The method of assimilation selected in the EcoFish model takes as input the values of a given variable $V_{mod}$ obtained from the calculations of the model and satellite measurements $V_{sat}$. Moreover, the method accepts a number of parameters that control its behavior and describe the data source. The most important of them are:

• data_type—allows you to specify the frequency with which data for assimilation appears, e.g., annually, monthly, every N hours [value used: N hours].
• data_inc—in the case of data appearing every N hours, specifies the number of N [value used: 24].
• interp_freq—determines how often information from assimilated data is entered into the model calculations, e.g., every N hours, every time step [value used: every time step].
• interp_type—defines the way in which assimilation data are interpolated between the frequency resulting from data_type and the one resulting from interp_freq. The possible options are nearest neighbor algorithm, linear interpolation, and third-order polynomial interpolation using the four nearest points on the timeline [value used: Linear].
• interp_inc—parameter specifying the frequency with which the differences between the model and measurement data are calculated [value used: 1 h].
• restore_tau—this is a parameter that specifies the time after which the model results should reach a value consistent with the measurement data [value used: 0.1 day].

With each calculation step, each assimilation module checks, on the basis of the data_type and data_inc parameters, whether new assimilation data should appear in a given step. If so, it loads the next file with assimilated data $V_{sat}$. For the sake of example, let us assume that data appears every 24 h. Of course, these data should not be entered into the model at once, in one time step, as this would disrupt the continuity of equations and the equilibrium of the system. Hence, using the interp_freq parameter, one can choose that the data should be entered gradually, e.g., every 0.5 h. Using the restore_tau parameter, one can specify that the model should reach the assimilated values after a period of 12 h. Having these parameters, the module divides the current difference between $V_{sat}$ and $V_{mod}$ into the number of steps resulting from interp_freq that fall within the restore_tau period, i.e., in this case by 24.

$$d{V}_{step}=(V_{sat}-V_{mod})/(restore\_tau/interp\_freq)$$

(1)

$$=dV/(restore\_tau/interp\_freq),$$

(2)

Here, $d{V}_{step}$ is a partial increment introduced to the model in a given assimilation step (0.5 h in this example). The value of a given model variable depends on many factors, e.g., transport, radiation, biological processes, etc. Therefore, the difference dV calculated at the beginning between the model data and the measurement data must be constantly corrected to obtain the expected value at the end. Hence, it is updated at the frequency specified by the interp_inc parameter. The resulting value of the assimilated variable is calculated by adding the calculated increment to the model result:

$$V_{assim}=V_{mod}+d{V}_{step},$$

(3)

The figures below present the application of the satellite data assimilation module in the EcoFish model for two selected days from the simulation period. On the left side, one can see the satellite image for the surface temperature, in the middle, the model result with visible effect of assimilation, and on the right side, the results from the model version without the assimilation. The first scene (Figure 3) was taken on 28 April 2019. On that day, due to the heavy cloud cover, the satellite image was severely restricted and provided information only about a small area within the domain (Figure 3a). As a result of the assimilation module, the surface temperature in the vicinity of the Hel Peninsula and the eastern coast of the Gulf decreased, which can be seen in the Figure 3b. Figure 3c shows the surface temperature from the version of the model without the assimilation.

In the next figure (Figure 4) for 3 May 2019, the satellite image is more complete and almost the entire visible domain has been assimilated.

4. Results

4.1. EcoFish Model Validation

The accuracy of the EcoFish model results, in the period from January 2014 to December 2020, for water temperature (Section 4.1.1) and salinity (Section 4.1.2) was checked by comparing them with available in situ observations from the ICES database and measurements made with the MIDAS CTD instrument during fishing cruises. This was conducted for the two versions of the EcoFish model—one with the assimilation module enabled (EcoFish+A) and one without assimilation (EcoFish−A). The most important statistical quantities were determined, such as Pearson’s correlation coefficients (r), root mean square errors (RMSE), standard deviations (STD), and biases (in relation to means), which illustrate the tendency of the model to systematically overstate or underestimate the result.

4.1.1. Water Temperature

At first, we wanted to verify the impact of the assimilation of satellite SST module itself. Therefore, the surface temperature was validated for 2018 using two separate versions of the EcoFish model—one without (EcoFish−A) and one with satellite data assimilation (EcoFish+A). All other model parameters were identical. Results from both runs were then compared against assimilated satellite data.

Table 3. Statistical description of SST from model and satellite.

Source	Mean [°C]	Median [°C]	STD [°C]
Satellite	12.55	13.24	6.39
EcoFish−A	11.42	11.83	5.67
EcoFish+A	11.99	12.42	6.16

provides a statistical summary of the temperature obtained from all three sources to give a better overview of its characteristics.

Table 4. Statistical verification of SST from model calculations vs. satellite measurements.

Source	Pearson’s r	RMSE [°C]	Bias [°C]
EcoFish−A vs. Satellite	0.95	2.31	−1.12
EcoFish+A vs. Satellite	0.98	1.45	−0.56

contains comparison of both model versions against satellite data used for assimilation.

As one can observe, the differences between model and the satellite are larger in case of the model without assimilation (Table 4). Pearson’s correlation coefficient (r) increased from 0.95 to 0.98. The root mean square error (RMSE) decreased by almost 1 °C from 2.31 °C to 1.45 °C, and the tendency of the EcoFish model to systematically underestimate the results by −1.12 °C for the nonassimilated version decreased to −0.56 °C for the assimilated version. This confirms that the assimilation mechanism itself was designed and implemented properly and it yields significant changes in obtained results. It is worth noticing that the assimilation does not result in 100% agreement between satellite and model data. This can be contributed to several factors. Most importantly, in order to save disk space, results saved by the model are averaged over the period of 6 h. Satellite data are also averaged over the assimilation period, but the assimilation is designed to have the peak alignment of the data precisely at 12:00. Apart from that, the model surface layer is much thicker than the surface layer measured by satellites. Because of that, it would be wrong to exactly replicate satellite results in the model. The assimilation module is parameterized to leave some level of freedom between model and satellite data. Last, one must take into the account that even though satellite data are assimilated with every time step, each water cell in the model is subjected to vertical and horizontal currents that dissipate the assimilated information. Given the above, obtained results are satisfactory and prove that the assimilation module works as expected.

In order to additionally emphasize the impact of assimilation on the improvement of the model results, a separate comparison of the temperature in the surface layer itself (from 0 to 5 m) with the data from the ICES database was made. For the surface, within the model domain, 1082 observations from the ICES database were available. The result of this analysis is presented in the Taylor diagram (Figure 5) in the form of normalized statistical coefficients. Absolute statistical values are presented in tabular form (

Table 5. Statistical comparison of modeled surface temperature with the reference data from ICES.

Database	Pearson’s r	RMSE [°C]	STD [°C]	Bias [°C]
ICES (EcoFish+A)	0.99	0.70	5.75	0.01
ICES (EcoFish−A)	0.99	0.93	5.32	−0.40

).

The ability of the EcoFish model (with an active SST satellite data assimilation module and without) to correctly project the real environment conditions was verified by comparing the model results for temperature with all available observations at all depths. The result of this validation is presented in the Taylor diagram [27] (Figure 6) in the form of normalized statistical coefficients. Absolute statistical values are presented in tabular form (

Table 6. Statistical comparison of modeled temperature on all depths with the reference data from ICES and MIDAS CTD.

Database	Pearson’s r	RMSE [°C]	STD [°C]	Bias [°C]
ICES (EcoFish+A)	0.94	1.33	3.66	−0.36
ICES (EcoFish−A)	0.95	1.22	3.52	−0.28
MIDAS CTD (EcoFish+A)	0.87	1.83	3.57	−0.34
MIDAS CTD (EcoFish−A)	0.85	2.03	3.84	−0.25

).

The Pearson correlation coefficient (r) calculated between the assimilated model (EcoFish+A) and the data from the ICES database was 0.94. When compared with data from fishing cruises using the MIDAS CTD instrument, it took the value of 0.87. The decline may be related to the varying density of in situ data from surface to bottom. ICES data was relatively homogeneously distributed in the water column, while the cruise data most often occurred at fishing depths, i.e., 30 to 60 m. Due to the use of assimilation, the model better reflects the temperature closer to the surface, as indicated by high correlations that slightly decrease with depth.

Table 6 shows also that when comparing to ICES data, a nonassimilated version of the model (EcoFish−A) produced slightly better statistics than the assimilated version (EcoFish+A). This might be related to the database itself and should not be taken as a sign that assimilation worsened the results. It is opposite in the case of MIDAS CTD data in which statistics for EcoFish+A are better than for the version without assimilation. Summarizing, high correlations and low RMSEs were recieved from both versions of the model.

The mean square error (RMSE) for EcoFish+A is 1.33 °C when compared with ICES data and 1.83 °C when compared with cruise data. The model has a similar bias for both in situ databases of −0.36 °C and −0.34 °C, respectively. This means that the model tends to systematically underestimate the results slightly. The standard deviation for both databases used during the validation is similar and amounts to 3.66 °C for ICES data and 3.57 °C for data from the MIDAS CTD instrument (Table 6).

When analyzing the vertical profile (Figure 7), created while taking all observations from the ICES database into account, compared to the corresponding values from the EcoFish model (with and without assimilation), a high correlation can be seen, lasting from the surface up to about the 13th level of the model (to a depth of 80 m).

Below the 13th level, the data are less correlated and the EcoFish model has a tendency to slightly underestimate the results. The reason for this is that the POP model has KPP implemented for surface layer only. Since it is designed for global issues, the vertical mixing scheme has been modified for better representation of surface layer in the Baltic Sea. Small changes of the interior shear mixing, suggested by Durski et al. [28], have been introduced. For better reproduction of the bottom layer, the dependence of the quadratic drag formula on thickness of the lowest model cells was applied (the logarithmic profile of roughness height). There is no turbulent closure though that will cover the bottom layer, which results in the underestimation of temperature (Figure 7) and salinity (Figure 8) in the bottom layers.

The most important thing is that the model correctly reflects the temperature drop in the thermocline layer (on average from the 3rd to the 9th depth level). Not only is a high correlation visible, but close and overlapping ranges of the double standard deviations are also visible. Only below the 7th level (below the depth of 35 m) are the model data characterized by a smaller standard deviation than the observational data from the ICES database.

Therefore, it can be concluded that, despite the slight discrepancies between the model results and the observations (mostly at greater depths), the vertical mixing in the EcoFish model has been correctly implemented, and the model itself reflects real conditions well.

4.1.2. Salinity

Another physical variable derived from the EcoFish model that we validated is salinity. Salinity is a good parameter to check if the model is capable of handling water masses, as it does not undergo any transformations (gains and losses) in the marine environment. Salinity results from both versions (with and without assimilation) of the model were compared with available in situ observations from the ICES database using the same locations as for temperature (Figure 2). The result of this comparison is presented in the Taylor diagram (Figure 6) in the form of normalized statistical coefficients, as well as in the form of absolute values in table (

Table 7. Statistical comparison of modeled salinity with the reference data from ICES.

Database	Pearson’s r	RMSE [PSU]	STD [PSU]	Bias [PSU]
ICES (EcoFish+A)	0.94	0.80	1.27	−0.01
ICES (EcoFish−A)	0.92	0.91	1.20	0.01

).

The Pearson correlation coefficient (r) calculated between the model data (EcoFish+A) and the observations from the ICES database took the value of 0.94, which is better than in the case of the nonassimilated version of the model. The root mean square error (RMSE) was 0.8 PSU; this is a satisfactory result, while having relatively large standard deviation of 1.27 PSU. The model has a low negative mean bias of −0.01 PSU, which could signify that it responds well to changes in salinity. However, this is largely due to the fact that at low and medium depths (from the surface to about 14th level), the model results for salinity are slightly higher than the ICES observational values, followed by a trend that reverses. At higher depths, the model begins to underestimate salinity from about 0.5 up to 2.0 PSU. This was demonstrated on a vertical salinity profile (Figure 8) created using all observations from the ICES database.

When analyzing the vertical profile, several characteristic zones in the water column can be seen. On the surface, we observe an increased standard deviation, both for model data and observations. It is the result of mixing fresh waters from river runoff with sea waters, causing increased salinity dynamics on the surface. Then, between 10 and 40 m deep (up to 60 m depending on the location), the isohaline layer stretches, which is noticeable both at a constant average salinity of about 7–8 PSU and the size of the standard deviation, which in this layer is the smallest throughout the entire water column. Below 35 m, the STD begins to rise gradually, reaching about 2 PSU by 70 m and remaining at this value to the bottom. Below the isohaline layer, there is a transition layer with a clearly delineated halocline, especially for the curve determined using ICES observations. Average salinity starts to increase systematically from about 55 m (11th level) and stabilizes only at a depth of 100 m (20th level). The curve determined using the model data also shows the presence of a halocline, but it is not so clearly marked. The model results do not have the same dynamics as in situ data, which is especially visible in a much smaller STD than in the case of observations. In the water layer from the 12th level to the bottom, the salinity obtained from the EcoFish model increases from about 9 PSU to 12 PSU, while the increase in salinity for the experimental data is greater and goes from 8 PSU to 13 PSU (Figure 8). The highest salinity values seen in the experimental data can be related to the infusion effect, while decreases can occur during periods of long-term stagnation.

4.2. EcoFish Model Simulation Results

In this section, we present the average monthly temperatures, salinity, sea surface height, and currents in the surface layer for EcoFish model with an active SST satellite data assimilation module. The averages reflect the simulation period from 2014 to 2020. The results for individual months have been transferred to the Appendix A section (Figure A1, Figure A2, Figure A3, Figure A4, Figure A5, Figure A6, Figure A7 and Figure A8 and

Table A1. Monthly means for surface temperature for the years 2014–2020.

Year\Month	January	February	March	April	May	June	July	August	September	October	November	December
2014	4.62	2.48	3.43	6.17	10.36	14.02	19.02	19.56	16.39	12.44	8.77	5.33
2015	4.09	3.48	3.92	5.28	9.11	13.84	16.94	18.52	16.36	12.13	7.85	7.22
2016	4.48	4.08	4.02	5.90	11.34	15.69	18.16	18.67	17.88	11.34	8.02	5.62
2017	3.85	3.34	3.61	5.12	9.52	13.58	16.46	18.12	16.21	12.42	8.94	6.16
2018	4.71	3.17	2.05	4.98	12.08	16.86	19.32	21.23	18.13	13.29	9.45	6.17
2019	4.28	3.66	3.84	6.10	9.20	17.28	17.74	19.47	16.58	12.92	9.70	7.05
2020	5.45	4.85	4.90	6.19	9.11	14.77	17.89	19.68	17.18	13.30	9.13	7.13
mean	4.50	3.58	3.68	5.68	10.10	15.15	17.93	19.32	16.96	12.55	8.84	6.38

,

Table A2. Monthly minimums for surface temperature for the years 2014–2020.

Year\Month	January	February	March	April	May	June	July	August	September	October	November	December
2014	−0.43	−0.43	0.60	1.33	3.28	3.94	9.81	10.81	2.24	2.48	1.29	0.38
2015	0.38	0.14	0.67	1.13	3.77	2.91	7.94	7.62	7.94	2.78	0.89	1.17
2016	−0.40	0.66	0.82	1.54	4.37	2.37	3.17	6.19	8.04	4.18	1.10	0.83
2017	0.05	−0.19	0.46	1.30	2.79	1.82	3.83	10.48	3.41	2.60	2.29	0.64
2018	0.17	−0.38	−0.41	0.74	3.81	5.07	6.39	8.85	7.14	4.49	1.06	0.88
2019	−0.20	0.22	1.30	2.47	2.05	9.74	8.40	13.60	3.70	3.53	2.86	1.27
2020	0.78	1.48	0.81	2.26	4.55	8.09	9.80	13.86	11.22	3.75	1.12	1.33
mean	0.05	0.21	0.60	1.54	3.52	4.85	7.05	10.20	6.24	3.40	1.52	0.93

,

Table A3. Monthly maximums for surface temperature for the years 2014–2020.

Year\Month	January	February	March	April	May	June	July	August	September	October	November	December
2014	6.75	6.44	9.42	16.51	20.22	21.08	28.45	26.47	23.56	15.56	11.78	7.73
2015	5.46	5.12	10.47	18.06	20.32	21.15	23.96	24.50	21.87	16.71	11.50	8.85
2016	7.42	6.71	11.78	14.77	20.19	24.40	24.23	22.58	20.85	17.05	10.60	8.50
2017	6.23	4.83	8.84	10.54	20.79	21.35	22.15	23.60	23.60	15.78	11.84	8.76
2018	6.87	4.71	9.13	16.41	23.02	22.86	27.26	26.69	22.32	16.65	11.92	8.29
2019	5.95	4.73	7.88	15.25	18.93	25.85	25.48	24.43	23.35	15.29	12.48	9.65
2020	6.95	5.84	7.54	15.04	17.19	25.16	28.31	26.66	20.53	18.24	12.45	9.46
mean	6.52	5.48	9.29	15.22	20.09	23.12	25.69	24.99	22.30	16.47	11.80	8.75

,

Table A4. Monthly standard deviations for surface temperature for the years 2014–2020.

Year\Month	January	February	March	April	May	June	July	August	September	October	November	December
2014	1.41	0.50	0.81	2.01	2.89	1.94	2.35	2.11	1.58	1.52	1.42	0.98
2015	0.59	0.50	0.53	1.26	1.74	1.65	1.22	1.55	1.26	2.24	1.65	0.75
2016	1.14	0.45	0.55	0.97	2.18	2.27	1.65	0.98	1.34	2.58	1.02	1.29
2017	1.10	0.64	0.63	0.79	3.04	1.69	1.43	0.72	1.03	1.49	1.16	1.06
2018	0.79	0.82	0.49	1.83	3.11	1.53	2.71	1.76	1.50	1.47	1.65	0.94
2019	0.84	0.48	0.36	1.50	1.90	2.36	1.42	0.84	2.12	1.08	1.16	0.85
2020	0.79	0.42	0.34	1.02	1.22	2.99	1.03	1.21	0.80	1.72	1.58	1.08
mean	0.95	0.54	0.53	1.34	2.30	2.06	1.69	1.31	1.37	1.73	1.38	0.99

,

Table A5. Monthly means for bottom temperature for the years 2014–2020.

Year\Month	January	February	March	April	May	June	July	August	September	October	November	December
2014	4.90	4.19	4.41	4.76	5.26	6.26	6.39	7.21	6.81	6.51	6.06	5.39
2015	4.78	4.52	4.68	5.10	6.04	7.08	7.99	7.34	6.95	6.55	6.31	6.13
2016	5.21	4.88	4.92	5.42	6.17	6.60	7.82	8.29	7.68	6.58	6.54	5.82
2017	5.08	4.95	4.93	5.38	5.84	7.47	7.78	7.71	7.62	7.26	6.50	5.49
2018	4.92	4.42	4.26	4.78	5.35	6.09	7.05	7.57	7.50	7.13	5.77	5.23
2019	4.72	4.69	4.79	5.22	5.93	6.64	8.31	7.66	8.01	7.42	6.37	5.72
2020	5.15	4.99	5.01	5.37	6.17	6.65	8.13	7.90	8.16	7.08	6.53	6.08
mean	4.97	4.66	4.71	5.15	5.82	6.68	7.64	7.67	7.53	6.93	6.30	5.69

,

Table A6. Monthly standard deviations for bottom temperature for the years 2014–2020.

Year\Month	January	February	March	April	May	June	July	August	September	October	November	December
2014	0.94	1.27	0.81	0.84	1.77	3.44	4.09	5.08	3.98	2.73	1.50	0.76
2015	0.87	1.01	0.75	0.68	1.80	3.32	4.63	4.38	3.55	2.46	1.30	0.78
2016	1.15	0.84	0.78	0.65	1.80	2.90	4.47	5.10	4.65	2.40	1.10	0.95
2017	1.41	1.44	1.22	0.69	1.61	3.51	4.13	4.51	4.15	2.98	1.71	0.87
2018	0.63	0.96	1.22	0.93	1.98	3.67	5.03	6.06	5.40	3.96	2.15	0.85
2019	0.86	1.02	0.82	0.75	1.45	3.21	4.82	4.57	4.37	3.22	1.85	0.82
2020	0.54	0.35	0.28	0.64	1.77	2.87	5.00	4.94	4.66	2.78	1.43	0.79
mean	0.91	0.98	0.84	0.74	1.74	3.27	4.59	4.95	4.39	2.93	1.58	0.83

,

Table A7. Monthly minimums for bottom temperature for the years 2014–2020.

Year\Month	January	February	March	April	May	June	July	August	September	October	November	December
2014	−0.43	−0.43	0.99	2.26	3.53	3.77	3.88	4.05	4.24	4.35	1.84	0.47
2015	0.80	0.41	1.22	1.87	4.37	4.37	4.43	4.47	4.62	3.08	1.51	1.77
2016	−0.40	1.44	1.62	2.68	4.35	4.30	4.05	4.45	4.65	4.74	1.98	1.12
2017	0.27	−0.05	0.94	2.38	3.39	4.56	4.27	4.38	3.99	3.73	2.99	0.92
2018	0.33	−0.24	−0.40	1.03	3.42	3.49	3.52	3.70	3.86	3.98	1.92	1.24
2019	0.03	0.25	1.98	2.84	3.06	4.56	4.51	4.51	4.89	4.82	3.52	2.28
2020	1.24	1.76	2.07	3.17	4.81	4.76	4.83	4.89	4.86	4.49	2.40	2.30
mean	0.26	0.45	1.20	2.32	3.85	4.26	4.21	4.35	4.44	4.17	2.31	1.44

,

Table A8. Monthly maximums for bottom temperature for the years 2014–2020.

Year\Month	January	February	March	April	May	June	July	August	September	October	November	December
2014	7.19	5.86	7.41	12.37	18.76	19.77	25.34	24.42	18.87	14.89	11.43	7.68
2015	6.58	5.68	6.23	10.89	14.08	17.64	20.52	22.49	19.11	15.60	10.82	8.79
2016	7.64	6.38	6.74	9.61	16.64	21.21	21.84	21.04	20.03	16.70	10.41	8.15
2017	6.60	6.49	6.88	8.48	17.38	18.80	19.87	20.31	19.14	15.30	11.05	8.98
2018	6.47	5.63	6.07	11.31	19.19	21.40	24.05	25.44	19.91	16.78	11.57	8.27
2019	7.13	6.79	6.80	12.44	14.78	22.47	21.71	21.74	22.23	15.13	12.00	8.72
2020	7.00	6.02	6.21	10.62	14.20	22.29	22.17	22.65	20.55	16.63	11.90	9.12
mean	6.94	6.12	6.62	10.82	16.43	20.51	22.21	22.58	19.98	15.86	11.31	8.53

,

Table A9. Monthly means for surface salinity for the years 2014–2020.

Year\Month	January	February	March	April	May	June	July	August	September	October	November	December
2014	7.71	7.76	7.52	7.31	7.36	7.40	7.35	7.35	7.40	7.46	7.51	7.59
2015	7.67	7.65	7.50	7.52	7.47	7.46	7.43	7.39	7.39	7.50	7.54	7.58
2016	7.67	7.66	7.45	7.35	7.40	7.37	7.40	7.38	7.38	7.57	7.58	7.61
2017	7.67	7.66	7.49	7.40	7.40	7.45	7.41	7.35	7.35	7.47	7.54	7.56
2018	7.63	7.60	7.45	7.39	7.35	7.37	7.38	7.38	7.39	7.47	7.50	7.55
2019	7.61	7.61	7.54	7.35	7.42	7.37	7.44	7.35	7.40	7.42	7.47	7.55
2020	7.59	7.65	7.52	7.46	7.44	7.33	7.40	7.36	7.35	7.43	7.47	7.53
mean	7.65	7.66	7.50	7.40	7.40	7.39	7.40	7.37	7.38	7.48	7.51	7.57

,

Table A10. Monthly minimums for surface salinity for the years 2014–2020.

Year\Month	January	February	March	April	May	June	July	August	September	October	November	December
2014	4.25	3.08	1.51	1.67	2.74	3.71	4.09	4.47	4.44	4.73	4.79	4.15
2015	3.27	2.73	1.99	2.40	3.13	3.92	3.96	4.37	4.24	4.92	4.70	4.00
2016	3.67	3.07	2.10	1.64	2.63	3.54	4.15	4.43	4.12	4.98	4.53	3.88
2017	3.50	2.92	1.92	1.72	2.81	3.85	4.03	4.01	4.23	4.97	4.62	3.50
2018	3.57	2.70	1.93	2.13	2.62	3.38	3.85	4.09	4.28	4.83	4.03	3.74
2019	3.64	2.59	1.89	1.72	2.55	3.57	4.13	4.27	4.60	4.55	4.46	3.01
2020	3.48	3.05	1.78	2.08	2.52	3.33	4.24	4.09	4.23	4.61	4.11	3.81
mean	3.62	2.88	1.87	1.91	2.72	3.61	4.06	4.25	4.31	4.80	4.46	3.73

,

Table A11. Monthly maximums for surface salinity for the years 2014–2020.

Year\Month	January	February	March	April	May	June	July	August	September	October	November	December
2014	8.65	8.70	7.98	7.77	7.75	7.67	7.66	7.55	7.70	7.81	8.15	8.15
2015	8.06	8.26	7.96	7.81	7.76	7.67	7.72	7.95	7.71	8.33	7.90	7.96
2016	8.32	8.02	7.85	7.76	7.75	7.73	7.63	7.56	7.71	8.56	7.86	7.91
2017	8.32	8.18	7.88	7.77	7.78	7.71	7.71	7.53	7.74	7.98	7.80	7.91
2018	8.70	7.95	8.00	7.89	7.75	7.63	7.62	7.62	7.68	7.77	8.65	8.66
2019	7.96	7.88	7.87	7.82	7.75	7.65	7.72	7.56	7.61	7.61	8.23	7.95
2020	7.89	7.93	7.99	7.81	7.78	7.66	7.68	7.67	7.58	7.78	7.74	8.16
mean	8.27	8.13	7.93	7.80	7.76	7.67	7.68	7.63	7.68	7.98	8.05	8.10

,

Table A12. Monthly standard deviations for surface salinity for the years 2014–2020.

Year\Month	January	February	March	April	May	June	July	August	September	October	November	December
2014	0.29	0.46	0.57	0.70	0.50	0.35	0.32	0.24	0.25	0.22	0.25	0.29
2015	0.36	0.45	0.57	0.49	0.46	0.37	0.30	0.26	0.27	0.22	0.24	0.30
2016	0.35	0.44	0.60	0.64	0.53	0.37	0.28	0.26	0.27	0.22	0.24	0.29
2017	0.37	0.40	0.65	0.65	0.54	0.37	0.32	0.28	0.26	0.20	0.27	0.35
2018	0.39	0.56	0.62	0.64	0.57	0.39	0.32	0.26	0.26	0.21	0.29	0.35
2019	0.42	0.50	0.55	0.64	0.53	0.40	0.29	0.29	0.23	0.24	0.28	0.34
2020	0.40	0.43	0.62	0.63	0.52	0.43	0.30	0.33	0.37	0.30	0.35	0.35
mean	0.37	0.47	0.60	0.63	0.52	0.38	0.30	0.28	0.27	0.23	0.27	0.32

,

Table A13. Monthly means for bottom salinity for the years 2014–2020.

Year\Month	January	February	March	April	May	June	July	August	September	October	November	December
2014	9.46	9.72	9.47	9.64	9.70	9.55	9.63	9.55	9.61	9.62	9.67	9.57
2015	9.24	9.45	9.53	9.39	9.58	9.58	9.52	9.64	9.63	9.63	9.39	9.40
2016	9.56	9.35	9.49	9.60	9.64	9.63	9.52	9.51	9.63	9.70	9.43	9.24
2017	9.25	9.49	9.36	9.48	9.65	9.50	9.50	9.57	9.54	9.39	9.34	9.38
2018	9.59	9.47	9.60	9.65	9.69	9.60	9.53	9.56	9.55	9.38	9.63	9.60
2019	9.28	9.46	9.31	9.68	9.65	9.64	9.48	9.61	9.48	9.47	9.60	9.51
2020	9.34	9.34	9.35	9.47	9.59	9.61	9.55	9.52	9.50	9.51	9.44	9.48
mean	9.39	9.47	9.44	9.56	9.64	9.59	9.53	9.57	9.56	9.53	9.50	9.45

,

Table A14. Monthly minimums for bottom salinity for the years 2014–2020.

Year\Month	January	February	March	April	May	June	July	August	September	October	November	December
2014	5.33	5.49	3.82	3.62	4.02	4.71	5.56	5.45	5.32	5.90	6.69	5.16
2015	5.29	4.12	3.87	3.56	4.38	5	5.16	5.69	5.23	5.79	5.80	5.33
2016	5.10	4.73	3.48	3.50	4.61	4.71	5.25	5.24	5.45	5.72	5.37	5.17
2017	4.95	4.87	3.39	3.04	4.18	4.40	4.89	5.52	5.48	5.81	5.56	4.77
2018	4.84	4.13	4.71	3.66	4.06	4.86	5.20	5.59	5.55	5.86	6.19	5.13
2019	4.70	4.13	3.50	4.34	4.07	4.99	5.30	5.59	5.71	5.64	5.83	4.39
2020	4.66	4.89	3.53	3.67	3.91	4.97	5.36	5.05	4.62	5.44	5.21	5.05
mean	4.98	4.62	3.76	3.63	4.18	4.81	5.25	5.45	5.34	5.74	5.81	5.00

,

Table A15. Monthly maximums for bottom salinity for the years 2014–2020.

Year\Month	January	February	March	April	May	June	July	August	September	October	November	December
2014	12.45	12.52	13.04	12.62	12.71	12.62	12.64	12.67	12.61	12.75	12.45	12.82
2015	12.92	12.54	12.99	12.96	12.84	12.77	12.85	12.59	12.62	12.82	13.19	12.82
2016	12.55	12.71	12.61	12.72	12.73	12.62	12.59	12.61	12.76	12.80	12.50	12.83
2017	12.52	12.54	12.59	12.79	12.82	12.70	12.63	12.74	13.15	12.82	12.42	12.44
2018	12.70	12.39	12.59	12.80	12.75	12.70	12.57	12.85	12.85	12.89	12.43	12.51
2019	12.44	12.48	12.80	12.59	12.68	12.61	12.59	12.60	12.74	12.84	12.48	12.93
2020	12.40	12.58	13.21	12.67	12.75	12.81	12.76	12.58	12.59	12.11	11.91	11.40
mean	12.57	12.54	12.83	12.73	12.76	12.69	12.66	12.66	12.76	12.72	12.48	12.54

,

Table A16. Monthly standard deviations for bottom salinity for the years 2014–2020.

Year\Month	January	February	March	April	May	June	July	August	September	October	November	December
2014	1.39	1.47	1.59	1.68	1.74	1.74	1.69	1.74	1.66	1.59	1.54	1.62
2015	1.51	1.55	1.57	1.72	1.76	1.75	1.74	1.64	1.67	1.56	1.62	1.60
2016	1.50	1.54	1.60	1.72	1.73	1.68	1.73	1.75	1.68	1.55	1.64	1.61
2017	1.54	1.54	1.61	1.75	1.70	1.75	1.73	1.71	1.71	1.63	1.62	1.63
2018	1.54	1.53	1.51	1.68	1.74	1.74	1.73	1.72	1.70	1.57	1.54	1.59
2019	1.57	1.58	1.64	1.64	1.75	1.72	1.74	1.69	1.70	1.64	1.58	1.62
2020	1.58	1.60	1.56	1.70	1.79	1.72	1.77	1.64	1.60	1.42	1.49	1.33
mean	1.52	1.54	1.58	1.70	1.74	1.73	1.73	1.70	1.67	1.57	1.58	1.57

,

Table A17. Monthly means for sea surface height for the years 2014–2020.

Year\Month	January	February	March	April	May	June	July	August	September	October	November	December
2014	−2.58	−1.27	1.46	0.27	0.14	1.69	0.28	1.93	0.47	−1.21	−2.73	3.20
2015	4.59	1.37	0.37	3.26	1.23	2.00	3.25	−0.29	0.58	−0.76	3.57	4.34
2016	1.35	2.67	0.62	0.98	0.53	0.59	2.44	3.00	1.35	−1.81	1.96	5.54
2017	3.86	0.69	1.57	2.39	0.55	2.20	2.11	1.57	1.75	4.49	2.53	3.88
2018	0.09	−0.11	−1.34	0.22	0.40	1.93	2.23	1.95	3.66	2.41	−1.27	1.30
2019	2.79	2.27	2.84	-0.83	1.32	0.59	3.45	0.78	3.34	2.41	−1.56	3.49
2020	4.20	4.55	1.39	2.28	2.14	1.12	3.38	0.92	1.91	−0.48	2.55	−1.82
mean	2.04	1.45	0.99	1.22	0.90	1.44	2.45	1.41	1.87	0.72	0.72	2.85

,

Table A18. Monthly minimums for sea surface height for the years 2014–2020.

Year\Month	January	February	March	April	May	June	July	August	September	October	November	December
2014	−23.84	−13.86	−14.12	−7.34	−15.87	−4.55	−6.76	−9.82	−7.45	−15.93	−15.70	−13.04
2015	−12.53	−13.46	−21.62	−14.91	−12.23	−8.29	−10.68	−14.11	−7.47	−19.00	−29.58	−19.20
2016	−13.14	−16.97	−7.40	−9.86	−5.65	−8.77	−6.39	−5.45	−8.66	−31.09	−16.76	−23.97
2017	−14.86	−16.38	−8.11	−7.56	−10.31	−12.32	−7.46	−8.61	−12.05	−11.56	−9.23	−16.03
2018	−21.75	−16.80	−22.01	−12.01	−9.55	−6.52	−4.71	−7.78	−6.83	−18.41	−16.05	−13.08
2019	−12.71	−13.03	−15.27	−12.87	−11.73	−8.40	−6.49	−6.89	−13.27	−9.23	−15.90	−21.19
2020	−8.80	−9.19	−22.77	−7.21	−4.12	−15.11	−6.59	−5.57	−8.24	−31.79	−7.82	−16.38
mean	−15.37	−14.24	−15.90	−10.25	−9.92	−9.14	−7.01	−8.32	−9.14	−19.57	−15.86	−17.55

,

Table A19. Monthly maximums for sea surface height for the years 2014–2020.

Year\Month	January	February	March	April	May	June	July	August	September	October	November	December
2014	45.86	13.67	43.37	13.11	8.38	11.86	7.68	18.14	14.61	14.65	6.26	43.04
2015	77.21	30.20	38.32	43.02	20.88	15.22	24.09	9.21	14.85	21.09	51.51	59.79
2016	31.17	45.59	10.15	17.59	18.70	23.84	17.29	14.55	18.14	24.84	31.78	59.41
2017	33.82	29.94	19.70	27.80	19.65	15.75	17.50	15.95	49.66	42.08	28.32	40.60
2018	34.89	11.46	7.89	25.70	14.86	19.77	10.17	27.11	38.23	32.82	10.03	21.01
2019	32.40	20.54	36.61	7.64	16.73	13.90	21.35	8.73	30.37	27.21	15.10	54.94
2020	34.10	37.47	60.19	25.78	14.99	14.54	21.37	8.79	23.26	22.65	24.96	14.91
mean	41.35	26.98	30.89	22.95	16.31	16.41	17.06	14.64	27.02	26.48	23.99	41.96

,

Table A20. Monthly standard deviations for sea surface height for the years 2014–2020.

Year\Month	January	February	March	April	May	June	July	August	September	October	November	December
2014	7.61	3.81	5.29	2.35	2.84	2.27	1.90	3.47	2.97	3.34	3.07	6.57
2015	9.46	5.11	4.87	5.81	3.87	2.73	4.63	3.26	3.20	4.67	8.82	8.41
2016	5.94	7.20	2.74	3.83	2.32	3.10	2.77	2.95	2.95	5.52	5.80	7.27
2017	5.56	5.84	4.48	3.66	3.00	4.07	3.09	3.38	5.38	7.14	4.49	6.75
2018	5.73	3.14	4.07	4.71	2.73	2.77	1.80	3.50	5.09	6.18	3.21	4.40
2019	5.46	4.29	6.40	2.99	3.02	2.54	3.39	2.50	5.38	4.75	4.27	7.35
2020	5.36	6.46	6.59	4.48	2.57	3.53	3.73	2.04	3.55	5.07	5.06	4.52
mean	6.45	5.12	4.92	3.97	2.91	3.00	3.04	3.01	4.07	5.24	4.96	6.47

,

Table A21. Monthly means for surface currents for the years 2014–2020.

Year\Month	January	February	March	April	May	June	July	August	September	October	November	December
2014	8.98	5.02	5.48	4.94	6.33	6.25	7.88	6.78	7.39	6.18	5.72	7.18
2015	8.43	6.76	5.87	6.56	6.23	5.69	7.10	9.13	7.12	8.18	8.71	7.86
2016	7.41	6.95	4.91	5.97	6.03	8.83	6.76	5.90	6.98	9.31	7.72	8.43
2017	7.84	6.97	4.90	5.58	6.11	7.75	6.65	6.52	6.83	8.78	7.12	8.08
2018	7.18	4.80	6.23	5.66	5.59	6.91	5.34	6.39	6.61	7.32	6.40	5.88
2019	7.41	6.42	6.72	6.14	5.78	7.20	7.40	6.05	7.53	5.82	6.32	7.02
2020	7.52	8.20	6.25	5.34	5.49	5.96	5.88	6.13	5.54	6.82	6.30	6.94
mean	7.82	6.44	5.77	5.74	5.94	6.94	6.72	6.70	6.86	7.49	6.90	7.34

,

Table A22. Monthly maximums for surface currents for the years 2014–2020.

Year\Month	January	February	March	April	May	June	July	August	September	October	November	December
2014	77.33	27.82	74.57	36.57	44.93	37.04	30.96	38.19	45.39	43.46	48.85	78.88
2015	120.09	60.55	90.82	77.49	48.70	27.68	70.34	56.30	46.57	52.13	84.40	89.04
2016	55.58	73.70	29.52	48.28	53.90	56.06	55.10	39.51	37.75	77.81	81.79	104.45
2017	60.38	66.74	46.19	70.15	46.20	50.08	38.65	28.88	51.69	67.66	57.29	84.60
2018	70.18	31.45	52.83	45.94	25.20	45.54	42.67	52.24	51.98	67.29	52.96	52.90
2019	70.52	38.52	72.50	33.80	51.43	33.49	44.28	26.03	55.87	51.12	42.51	51.77
2020	58.32	72.23	70.19	63.05	37.54	30.77	33.34	28.82	29.95	64.21	57.21	43.93
mean	73.20	53.00	62.37	53.61	43.98	40.10	45.05	38.57	45.60	60.53	60.71	72.22

and

Table A23. Monthly standard deviations for surface currents for the years 2014–2020.

Year\Month	January	February	March	April	May	June	July	August	September	October	November	December
2014	7.95	3.60	5.60	3.44	4.97	4.43	5.24	4.95	5.31	4.33	4.63	6.12
2015	8.72	5.73	5.66	6.20	4.32	3.60	5.72	6.91	5.07	6.28	7.85	6.20
2016	5.83	6.12	3.47	4.30	4.74	6.60	5.23	4.08	5.02	7.87	6.30	7.41
2017	6.18	5.97	4.00	5.04	4.38	5.49	4.89	4.47	5.40	6.95	5.27	6.73
2018	6.20	3.82	5.45	4.12	3.71	4.96	3.88	4.69	4.76	6.11	5.46	4.60
2019	5.97	4.27	5.61	4.18	4.14	5.02	5.56	4.03	6.04	4.17	4.73	5.17
2020	5.15	6.56	5.23	4.81	3.95	4.11	4.07	4.35	3.85	5.81	5.10	5.05
mean	6.57	5.15	5.00	4.59	4.32	4.89	4.94	4.78	5.06	5.93	5.62	5.90

). Additionally, figures with the differences between the monthly averages of parameters from the models with (EcoFish+A) and without (EcoFish−A) assimilation are presented.

4.2.1. Water Temperature

The model domain is characterized by a strong seasonal variability of the surface temperature (Figure 9) for each year from the seven-year simulation (2014–2020). The greatest dynamics occurs in the southern part of the domain, which includes the southern part of the Gulf of Gdańsk and the Bay of Puck, which has the greatest number of low-depth coastal areas that react quickly to atmospheric forcing. The remaining regions are characterized by relatively lower seasonal variability of the surface temperature.

The mean water surface temperature for the entire analyzed model domain was 10.43 °C. The months with the lowest average temperature are generally February and March, and the coldest month in the simulation period was March 2018 with an average temperature of 2.05 °C. The warmest months are usually the summer ones, i.e., July and August with the record-breaking August 2018, in which the average water temperature in the surface layer reached 21.23 °C (Figure A1 and Figure A2 and Table A1).

Temperature extremes for single model cells were most common in shallow coastal regions. The most characteristic is the shallow inner Bay of Puck called Puck Lagoon (Figure 1), which is not only separated from the open sea by the Hel Peninsula, but in its eastern part, there is a characteristic bathymetric anomaly in the form of shallow water (marked with curved dashed line), which additionally limits the exchange of water masses with the outer Bay of Puck (and whole Gulf), influencing to local temperature extremes. The lowest temperatures were in January and February 2014, falling to −0.43 °C (Table A2), and the highest were in July 2014 and 2018, when the temperature exceeded 28 °C (Table A3).

The lowest standard deviations ranging from 0.34 °C to 0.81 °C (0.53 °C on average) were obtained by the model for February and March. It is the period before spring when the surface layer is cooled down after winter, and both air temperature and sunlight do not yet reach high values to cause significant local changes. The largest deviations from the mean surface temperature appear in May and June (1.22 °C to 3.11 °C) with values exceeding 3 °C in May 2017 and 2018 (Table A4).

The picture below (Figure 10) presents the average monthly surface temperature for the period 2014 to 2020. It can be seen that there are four characteristic periods of temperature variation in the domain. The longest, five-month cold period, lasting from December to April, when the average surface temperature is low and relatively stable, ranging only from about 3 °C to 7 °C. Then, a four-month warm period lasting from June to September with average temperatures ranging from about 15 °C to 19 °C. There are also two transitional periods. The first transition (uptrend) period is May, when the temperature rises sharply from 5 °C in April to 15 °C recorded in June. The second transition period (downward) is October and November, when the water cools down quickly from an average of 17 °C in September to 6 °C in December (Table A1).

The reservoir that responds most quickly to external factors is the aforementioned Puck Lagoon. Thanks to its specific location and bottom topography, it has the greatest variability of the surface temperature and the minimum and maximum temperature achieved. In winter, local ice cover is observed, while in summer, it is exposed to toxic algae blooms stimulated by high temperatures and the deposition of inorganic phosphate from rivers.

Looking at Figure 11, that shows the difference in the monthly average SST values between the model with (EcoFish+A) and without assimilation (EcoFish−A), it can be seen that the assimilation influences the increase of the temperature in the warm season (from May to August) and the decrease in the cold one (from October to January). It is related to the vertical resolution of the model, and more precisely to the thickness of the first (surface) layer, which is 5 m.

It is more than the actual surface layer for which the SST is measured from satellite instruments. A thicker layer responds slower to atmospheric forcing, as it has a higher heat capacity. Assimilation of the satellite data into the model adjusts the surface layer temperature to the atmospheric conditions faster; hence, it responds faster to the changes.

4.2.2. Salinity

During the seven-year-long simulation, the average monthly salinity in the surface layer was between 7.31 PSU and 7.76 PSU, which gives an average of 7.47 PSU for the entire time period (Figure 12 and Figure 13). The annual course of salinity in the study area is usually established assuming lower values in the warm/summer months (minimum for April 2014) and higher values in the cold/winter season (maximum in February 2014) (Figure A1 and Figure A2 and Table A9).

Figure 14 shows that there are differences in surface salinity distribution when comparing models with and without SST assimilation. The model with assimilation (EcoFish+A) gives almost 1 PSU higher salinity in the south area of Gulf of Gdańsk from May to August. The reason for that is the increase in water circulation (Section 4.2.4 ) leading to more salty waters located in the deeper bottom layers being transported to the surface as a result of mass conservation law.

The lowest seasonal fluctuations in salinity occur in the open sea, which is confirmed by small standard deviations (Table A12), rarely exceeding 0.3 PSU. In the southern part of the domain, which includes the mouth of the Vistula River, salinity can fluctuate from about 2 PSU to even 8 PSU in the summer months (Figure 13). The lowest salinity recorded in the model for the simulation period, amounting to 1.51 PSU, was recorded in March 2014 (Table A10). It was the result of the spring rise and runoff from the Vistula River. The highest of 8.70 PSU was obtained for January 2018 at open sea (Table A11).

The dynamics of changes in salinity along the surface layer is influenced by a number of factors. Among others, it is the amount of river runoff, seasonal changes in the thermal structure of water or changing meteorological conditions. However, in the bottom layer, the salinity distribution over the year seems to be relatively uniform, strongly related to the bathymetry (Figure 15). The highest salinity at the bottom (12.66 PSU on average) occurs in areas of great depth, in particular in the Gdańsk Deep. Possible fluctuations there, are no longer the result of cyclical processes with a seasonal frequency, but rather, of irregular events such as sea inflow. Only in 3 out of 84 considered months, the average monthly salinity at the bottom exceeded 13 PSU (Table A15). This situation occurred in March 2014 (13.04 PSU), September 2017 (13.15 PSU) and November 2015 (13.19 PSU).

4.2.3. Sea Surface Height

The lowest values of sea surface height determined in the model were −29.58 cm in November 2015 and −31.09 cm in October 2016 (Table A18). The highest, 60.19 cm and 77.21 cm, were obtained for March 2020 and January 2015, respectively (Table A19).

The average sea surface height was 1.50 cm (Figure 16 and Table A17). Individual monthly averages are characterized by higher standard deviations (between 4.96 cm and 6.47 cm) in the months from October to February (Table A20). In the remaining months, the average standard deviations are usually smaller and reach values of about 3 cm (Figure 17).

The process of SST assimilation has minor but noticeable influence on sea level (Figure 18). The increase of salinity in the coastal area (Figure 14) results in higher density, which has direct impact on pressure distribution. Therefore, an increase in salinity causes a decrease in sea level, keeping the hydrostatic balance of the system.

4.2.4. Currents

The spatial distribution of sea currents inside the domain is much more characteristic and repeatable than in the case of sea surface height. The average current velocity in the surface layer for 2014–2020 was 6.73 cm·s${}^{-1}$ with an average standard deviation of 5.23 cm·s${}^{-1}$ (Figure 19 and Table A21 and Table A23). The strongest currents were obtained for December 2016 and January 2015 and reached the speed of 104.45 cm·s${}^{-1}$ and 120.09 cm·s${}^{-1}$ (Table A22), respectively.

Inside the domain, a characteristic area can be distinguished in which the strongest currents exceeding 20 cm·s${}^{-1}$ were modeled. It is a coastal strip stretching along the entire Hel Peninsula from the open sea (Figure 20).

This is also an area of frequent coastal upwelling, which causes cold water masses to rise from the bottom to the surface. The process responsible for this phenomenon is the Ekman transport, associated with the persistence of the southeastern wind running along the Hel Peninsula. For example, the August 2015 current map (Figure A8) shows a strong northwesterly current along the peninsula due to winds blowing in August, resulting in upwelling. The surface temperature map from 25 August 2015 (Figure 21) shows a large horizontal gradient. Gradients observed in this region are often reaching up to 5 °C·km${}^{-1}$ [29].

Temperature has a direct effect on the density of water, and the density becomes lower as the temperature increases. As the result of such modification, the same wind stress gives stronger currents because of the second law of dynamics, which is presented as the difference between assimilated and nonassimilated sea currents (Figure 22). Consequently, bigger sea currents increase water circulation in the coastal areas of Gulf of Gdańsk.

Images of current roses in the surface layer for selected three characteristic regions within the domain (Figure 2) are presented below.

The VR region (Vistula River) covers the coastal and shallow, southern part of the Gulf of Gdańsk within the mouth of the Vistula River. Monthly averages of surface currents in this area rarely exceed 16 cm·s${}^{-1}$ (Figure 23). In this region, eastern currents constitute the dominant part of directions. In the months from December to April, they have 39% and a greater share of all directions. Such current direction causes that the water flowing out of the Vistula has a difficult outflow and is distributed to the east along the shore of the Gulf. The long-term presence of such currents limits the spread of river waters and reduces the zone of fresh and sea water mixing.

In the GD region (Gdańsk Deep), which covers the deepwater area of the domain, located directly above the Gdańsk Deep, both the distribution of average velocities and directions is much more homogeneous than in the case of other regions (Figure 24). This is due to the high variability of wind directions and velocities over this area. Moreover, due to the great depths occurring here, the bathymetry does not have such a strong influence on the distribution of currents as in the case of areas close to the coast. From November to February, statistically more often there are currents heading in the eastern, northeastern and southeastern directions (about 60% of cases), but in the remaining months, the situation is less diversified. For example, in the summer months (from June to September), the southeast, south and southwest are dominant directions. They account for 48.6% in June, 57% in July, 58.3% in August, and 53.6% in September. In this region, the average monthly current speeds are comparable to those obtained for the VR region. Currents with speeds in the range 4–16 cm·s${}^{-1}$ often constitute even 60–70% of all velocities here. Moreover, in each month, a small share of current velocities exceeding 16 cm·s${}^{-1}$, and sometimes even 24 cm·s${}^{-1}$, can be found.

In the model results for HP (Hel Peninsula) region, we observe the highest average monthly current velocities in the entire domain (Figure 25). Average values exceeding 24 cm·s${}^{-1}$ appear here every month and constitute from 3 to 22% of all speed ranges. The directions of surface currents are specific in this region. In each month, the dominant directions are northwest (prevailing in the warm months, from May to November) and southeast (in other months). Together, they constitute over 60% of all currents in each month. Such structure of surface currents enables rapid movement of water masses along the Hel Peninsula, mixing together the Gulf of Gdańsk and Baltic Proper waters. The surface current distribution in the vicinity of Hel Peninsula is mostly induced by dominating westerly winds [30], but also depends on the large-scale internal water cycle in the Baltic Sea [31].

The current velocities in the bottom layer along the VR and HP regions rarely exceed 4 cm·s${}^{-1}$. Only in GD they have a higher share of over 10%, especially from October to February. The rose of currents for the Gdańsk Deep indicates the existence of a dominant northern bottom current (Figure 26). This suggests that the waters at the bottom are most often pushed toward the Gotland Basin. On the monthly average maps (Figure A9), from December to March, however, the dominance of the southern current can be observed. It moves the water masses in the shallow-water direction of the southern part of the Gulf of Gdańsk.

5. Discussion

This paper presents the hydrodynamic part of the three-dimensional numerical model EcoFish. The model has been used to simulate the hydrodynamics of the Gulf of Gdańsk. EcoFish has a satellite data assimilation module for SST, which uses data from the SatBałtyk project database, consisting of photos from a medium-resolution imaging spectroradiometer (MODIS AQUA) and an advanced ultrahigh-resolution radiometer (AVHRR). The task of this module is to assimilate the available surface temperature satellite data into the model domain in order to improve the simulation results, allowing for better determination of the dynamics of changes in physical parameters. The EcoFish model covers the South Baltic Sea and, more precisely, the entire Gulf of Gdańsk together with the Bay of Puck. The model domain is connected via an open boundary with the Baltic Sea from the west and the north.

The article presents statistical validation of the EcoFish model, which allowed to verify the correctness of the results obtained from it in terms of seasonal and spatial variability of the simulated water temperature and salinity. For this purpose, the available in situ observations from the ICES databases were used, along with the database created during fishing cruises carried out under the tasks of the FindFish Knowledge Transfer Platform. For the entire analyzed simulation period from January 2014 to December 2020, basic statistical values were determined, such as root mean square errors (RMSE), standard deviations (STD), and Pearson correlation coefficients (Section 4.1).

The validation showed that the EcoFish model results for water temperature were consistent with in situ observations. To confirm this, two experimental databases were used. Almost 18,000 measurements were available in the ICES database, distributed relatively evenly throughout the domain, except for the shallow region along the coast where no monitoring was carried out, or at least data from this region were not publicly available (Figure 2). The correlation of the EcoFish model with these data (ICES) was 0.94 with the root mean square error (RMSE) of 1.33 °C. As a result of comparing the modeled temperature against the data from the database created during fishing cruises, a correlation coefficient of 0.87 were calculated. This is a satisfactory result, taking the strong concentration of cruise data in the belt from the mouth of the Vistula River in the northwest direction into account. Thus, the data come both from the area where there is mixing of river waters (from the Vistula River) with the waters of the Gulf and from the area where the strongest currents occur in the entire domain (the belt along the Hel Peninsula). It should also be noted that most of these data came from fishing depths, i.e., 30 to 60 m, where the impact of SST satellite data assimilation is no longer visible.

The correlation of the model results for salinity with the ICES data at the level of 0.94 and the low root mean square error of 0.8 PSU suggest that the model copes well with the transport of water masses. It also proves that the rivers in the model have been correctly implemented and that the outgoing freshwater is correctly mixed with the saltwater of the Gulf and distributed by currents in its area. Additionally, when analyzing the vertical profile (Figure 8), both the isohaline layer and the formation of a halocline at lower depth levels can be seen, which proves that the model correctly reflects the dynamics of salinity changes in the water column.

When analyzing the seven-year simulation period of the EcoFish model (from January 2014 to December 2020), it can be observed that the temperature of the Gulf of Gdańsk waters is subject to strong seasonal changes and depends mainly on changes in air temperature and solar radiation. They are also largely influenced by convection processes and wind-induced mixing. The changes in the water temperature of the Gulf also show the influence of the Vistula River, whose waters increase the temperature in the Gulf in spring and summer and lower it in autumn. The lowest values of surface water temperature occur in January and remain at the level of about 0.1 °C (Table A2). On the other hand, the lowest average values of surface water temperature in the entire domain occur in February (Table A1). During this month, the surface waters of the entire reservoir are characterized by a similar temperature, and the differences do not exceed 2.5 °C. In the following months, the temperature of surface waters increases (the fastest in the coastal zone). The highest spatial differentiation is observed in the model results for May and June (differences amounting to about 7 °C). The highest average surface water temperatures occur in August (Table A1).

The location of the Gulf of Gdańsk and its specific bottom topography favor the occurrence of salinity diversification. Significant differences in its distribution occur between the shallow coastal area and the deeper part of the Gulf, which resembles the waters with a layered structure typical of the Baltic Sea (with the presence of a halocline and a thermocline). The shallow-water coastal zone of the Gulf of Gdańsk is influenced by fresh waters entering it from rivers and other types of surface runoff. The Vistula River has the greatest impact on changes in salinity, with huge volumes of fresh water flowing out (average flow exceeding 1000 m${}^3$/s), causing local salinity drops below 7 PSU. Its influence is also noticeable in the surface layer of the deep-water part of the Gulf of Gdańsk, mainly in the spring season, when, due to currents, river waters mix with sea waters and are carried into the Gulf.

When analyzing the distribution of currents in the studied domain, a characteristic area can be distinguished, stretching along the Hel Peninsula. The strongest surface currents occur there, often exceeding 20 cm·s${}^{-1}$. Two directions dominate there, depending on the season. Northwestern currents are mainly observed in the model results for the summer months, pushing the water from the Gdańsk Basin toward the open sea and are accompanied by the formation of coastal upwelling and downwelling. In the remaining months, southeastern currents predominate in this region, carrying waters toward the inner Gulf of Gdańsk. The distribution of surface currents around the mouth of the Vistula is also peculiar, where the most common is the eastern current, which distributes the waters flowing out of the Vistula along the shore of the Gulf. Its long-term presence limits the spread of the Vistula waters and reduces the zone of mixing fresh water with sea water. HP and VR regions are two specific regions along the Polish coastline where coastal up- and downwelling events occurs. This is induced by several factors, which the most important are the dominating westerly winds [30], bathymetry and vicinity of the coastal formation. In the HP region, in addition, the large-scale circulation of the Baltic Sea with the surface current pushing waters along the Hel Peninsula into the Gulf of Gdańsk [31] is responsible for the currents distribution.

The factor that has the greatest impact on changes in the sea surface height is wind. Certain areas can be distinguished with the greatest variation in the SSH. These are coastal areas, in particular around the Hel Peninsula, the southern coast stretching from the Bay of Puck, along the Vistula Spit, as well as the eastern shore of the Gulf of Gdańsk (Figure A5 and Figure A6).

6. Conclusions

In this paper, we present a numerical model of the Gulf of Gdańsk EcoFish model with an active module of satellite data assimilation for surface temperature. This version of the EcoFish model is being developed and used within the framework of the project “FindFish Knowledge Transfer Platform—Numerical Forecasting System for the Marine Environment of the Gulf of Gdańsk for Fisheries”. EcoFish is the basic element of the platform that provides fishermen and scientists with the current and forecast hydrodynamic, chemical, and biological conditions of the Gulf of Gdańsk. It also produces forecasts determining the most favorable environmental conditions for the occurrence of industrial pelagic fish in the South Baltic region. The aim of this research and development project is to increase the intensity of knowledge transfer and the use of scientific potential by fishermen, and consequently contribute to the sustainable development of sea fisheries and increase the protection of the Gulf of Gdańsk ecosystem.

To verify the correctness of the EcoFish model, a statistical analysis was carried out by comparing the model results with the in situ observations for the simulation period from January 2014 to December 2020. Satisfactory results were obtained and the compliance of the model results for water temperature and salinity with the available observations was confirmed. Correct mapping of the physical conditions inside the domain allows the model to be used for further simulations with an active part of the ecosystem. To do this, it is required to have a model that correctly simulates the physical conditions of mixing in a water body and heat exchange, controlling the heating and cooling of water masses. This is of great importance for the simulation of biochemical factors and the primary production process that will be conducted by the biochemical part of the EcoFish model.

The decision to validate the model for water temperature and salinity resulted from the fact that these two parameters serve as input data for the Fish Module, in which the Habitat Suitability Index maps are determined based on the environmental preferences of fish. The final product of the project will be sharing the FindFish platform as a website that will provide all the results and forecasts in operational mode.