Sea Level Seasonal, Interannual and Decadal Variability in the Tropical Pacific Ocean
Abstract
:1. Introduction
2. Data and Methods
2.1. Datasets
2.2. Methods
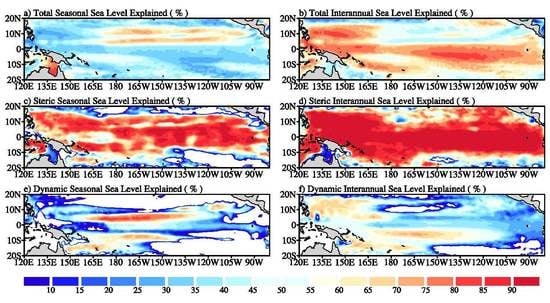
2.2.1. Calculation of Explained Variances Percentage
2.2.2. Multiple Variable Linear Regression Method
2.2.3. Steric Sea Level
2.2.4. 1.5-Layer Reduced-Gravity Model
3. Seasonal Sea Level Variations in the TPO
4. Interannual to Decadal Sea Level Variations in the TPO
4.1. Interannual Sea Level Variations in the TPO
4.2. Decadal Sea Level Variations in the TPO
4.3. Interannual to Decadal Sea Level Variations in the TPO
4.4. Interannual and Decadal Sea Level Fingerprints of TPO
5. Summary and Discussion
5.1. Discussion
5.2. Summary
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hallegatte, S.; Green, C.; Nicholls, R.J.; Corfee-Morlot, J. Future flood losses in major coastal cities. Nat. Clim. Chang. 2013, 3, 802–806. [Google Scholar] [CrossRef]
- Wong, P.P.; Losada, I.J.; Gattuso, J.P.; Hinkel, J.; Khattabi, A.; McInnes, K.L.; Saito, Y.; Sallenger, A. Climate Change 2014—Impacts, Adaptation, and Vulnerability. Part A: Global and Sectoral Aspects. Contribution of Work-ing Group II to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change. In Coastal Systems and Low–Lying Areas; Field, C.B., Barros, V.R., Dokken, D.J., Mach, K.J., Mastrandrea, M.D., Bilir, T.E., Chatterjee, M., Ebi, K.L., Estrada, Y.O., Genova, R.C., et al., Eds.; Cambridge University Press: Cambridge, UK, 2014; pp. 361–409. [Google Scholar]
- Church, J.A.; White, N.J. Sea-level rise from the late 19th to the early 21st century. Surv. Geophys. 2011, 32, 585–602. [Google Scholar] [CrossRef] [Green Version]
- Becker, M.; Meyssignac, B.; Letetrel, C.; Llovel, W.; Cazenave, A.; Delcroix, T. Sea level variations at tropical Pacific islands since 1950. Glob. Planet. Chang. 2011, 80, 85–98. [Google Scholar] [CrossRef]
- Zhang, X.B.; Church, J.A. Sea level trends, interannual and decadal variability in the Pacific Ocean. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]
- Merrifield, M.A.; Mathew, E.M. Regional sea level trends due to a Pacific trade wind intensification. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef]
- Qiu, B.; Chen, S.; Wu, L.; Kida, S. Wind- versus eddy-forced regional sea level trends and variability in the North Pacific Ocean. J. Clim. 2015, 28, 1561–1577. [Google Scholar] [CrossRef]
- Axel, M.; Mikael, C.; David, A.T.H.; Thomas, S. Ordovician and Silurian sea–water chemistry, sea level, and climate: A synopsis. Palaeogeogr. Palaeoclimatol. Palaeoecol. 2010, 296, 389–413. [Google Scholar] [CrossRef]
- Merrifield, M.A.; Thompson, P.R.; Lander, M. Multidecadal sea level anomalies and trends in the western tropical Pacific. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]
- Chen, D.; Cane, M.A.; Zebiak, S.E.; Kaplan, A. The impact of sea level data assimilation on the Lamont Model Prediction of the 1997/98 El Niño. Geophys. Res. Lett. 1998, 25, 2837–2840. [Google Scholar] [CrossRef]
- Chambers, D.P.; Chen, J.; Nerem, R.S.; Tapley, B.D. Interannual mean sea level change and the Earth’s water mass budget. Geophys. Res. Lett. 2000, 27, 3073–3076. [Google Scholar] [CrossRef]
- Christopher, G.P.; Rui, M.P. Buoyancy-driven interannual sea level changes in the southeast tropical pacific. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]
- Li, L.; Xu, J.; Cai, R.S. Trends of sea level rise in the South China Sea during the 1990s: An altimetry result. Chin. Sci. Bull. 2013. [Google Scholar] [CrossRef]
- Cazenave, A.; Llovel, W. Contemporary Sea Level Rise. Annu. Rev. Mar. Sci. 2010, 2, 145–173. [Google Scholar] [CrossRef] [Green Version]
- Anny, C.; Frédérique, R. Sea level and climate: Measurements and causes of changes. Wiley Interdiscip. Rev. Clim. Chang. 2011, 2, 647–662. [Google Scholar] [CrossRef]
- Merrifield, M.A. A Shift in Western Tropical Pacific Sea Level Trends during the 1990s. J. Clim. 2011, 24, 4126–4138. [Google Scholar] [CrossRef]
- Han, W.Q.; Meehl, G.A.; Hu, A.X.; Alexander, M.A.; Yamagata, T.; Yuan, D.L.; Ishii, M.; Pegion, P.; Zheng, J.; Hamlington, B.D.; et al. Intensification of decadal and multi-decadal sea level variability in the western tropical Pacific during recent decades. Clim. Dyn. 2014, 43, 1357–1379. [Google Scholar] [CrossRef]
- Hu, S.J.; Fu, D.Y.; Han, Z.L.; Ye, H. Density, Demography, and Influential Environmental Factors on Overwintering Populations of Sogatella furcifera (Hemiptera: Delphacidae) in Southern Yunnan, China. J. Insect Sci. 2015, 15, 58. [Google Scholar] [CrossRef] [Green Version]
- Lu, Q.; Zuo, J.C.; Wu, L.J. Low-frequency variation in sea level in the tropical Pacific. Haiyang Xuebao 2017, 39, 43–52. [Google Scholar] [CrossRef]
- Lu, Q.; Zuo, J.C.; Li, Y.F.; Chen, M.X. Interannual sea level variability in the tropical Pacific Ocean from 1993 to 2006. Glob. Planet. Chang. 2013, 107, 70–81. [Google Scholar] [CrossRef]
- Chen, J.L.; Shum, C.K.; Wilson, C.R.; Chambers, D.P.; Tapley, B.D. Seasonal sea level change from TOPEX/Poseidon observation and thermal contribution. J. Geod. 2000, 73, 638–647. [Google Scholar] [CrossRef]
- Yu, H.L. The characteristic of Northwest Pacific sea level variation, and influencing factor. J. Ocean. Univ. China 2013, 43, 9–20. [Google Scholar] [CrossRef]
- Li, X.H.; Wei, G.J.; Shao, L.; Liu, Y.; Liang, X.R.; Jian, Z.M.; Sun, M.; Wang, P.X. Geochemical and Nd isotopic variations in sediments of the South China Sea: A response to Cenozoic tectonism in SE Asia. Earth Planet. Sci. Lett. 2003, 211, 207–220. [Google Scholar] [CrossRef]
- Li, J.; Tan, W.; Chen, M.X.; Luo, F.Y.; Liu, Y.; Fu, Q.J.; Li, B.T. An extreme sea level event along the northwest coast of the South China sea in 2011–2012. Cont. Shelf Res. 2020, 196, 104073. [Google Scholar] [CrossRef]
- Busalacchi, A.J.; Mcphaden, M.J.; Picaut, J.; Springer, S.R. Sensitivity of wind-driven tropical Pacific Ocean simulations on seasonal and interannual time scales. J. Mar. Syst. 1990, 1, 119–154. [Google Scholar] [CrossRef]
- Sergey, V.; Vinogradov, R.M.; Ponte, P.H.; Carl, W. The mean seasonal cycle in sea level estimated from a data-constrained general circulation model. J. Geophys. Res. Ocean. 2008, 113. [Google Scholar] [CrossRef]
- Roberts, C.D.; Calvert, D.; Dunstone, N.; Hermanson, L.; Palmer, M.D.; Smith, D. On the Drivers and Predictability of Seasonal-to-Interannual Variations in Regional Sea Level. J. Clim. 2016, 29, 7565–7585. [Google Scholar] [CrossRef]
- Chen, X.; Qiu, B.; Cheng, X.H.; Qi, Y.Q.; Du, Y. Intra-seasonal variability of Pacific-origin sea level anomalies around the Philippine Archipelago. J. Oceanogr. 2015, 71, 239–249. [Google Scholar] [CrossRef]
- Chen, M.X.; Zuo, C.S.; Zhang, W.H.; Jia, Y.R.; Lyu, X.F. Research progress of inter-annual and multi-decadal sea level variability in tropical Pacific Ocean. J. Oceanogr. 2017, 45, 249–255. [Google Scholar] [CrossRef]
- Chang, Y.T.; Du, L.; Zhang, S.W.; Huang, P.F. Sea level variations in the tropical Pacific Ocean during two types of recent El Niño events. Glob. Planet. Chang. 2013, 108, 119–127. [Google Scholar] [CrossRef]
- Landerer, F.W.; Jungclaus, J.H.; Marotzke, J. El Niño–Southern Oscillation signals in sea level, surface mass redistribution, and degree-two geoid coefficients. J. Geophys. Res. Ocean. 2008, 113, C08014. [Google Scholar] [CrossRef] [Green Version]
- Wang, G.Q.; Jin, J.L.; Wan, S.C.; Zhai, R. Variation of sea level rise along the China coastal area during the past decades. In Proceedings of the 2015 Academic Annual Meeting of China Water Conservancy Society, Nanjing, China, 26–28 October 2015; Volume II. [Google Scholar]
- Li, L.H.; Zhou, L.H.; Lian, H.J. Sea-level Rise Forecast Model. J. Comput. 2011, 6, 2120–2126. [Google Scholar] [CrossRef]
- Han, W.Q.; Gerald, A.; Meehl, A.; Detlef, S.; Aixue, H.; Benjamin, H.; Jessica, K.; Hindumathi, P.; Philip, T. Spatial Patterns of Sea Level Variability Associated with Natural Internal Climate Modes. Surv. Geophys. 2017, 38, 221–254. [Google Scholar] [CrossRef] [Green Version]
- Meng, L.S.; Zhuang, W.; Zhang, W.W.; Ditri, A.; Yan, X.H. Decadal Sea Level Variability in the Pacific Ocean: Origins and Climate Mode Contributions. J. Atmos. Ocean. Technol. 2019, 36, 689–698. [Google Scholar] [CrossRef]
- Duan, J.; Li, Y.L.; Zhang, L.; Wang, F. Impacts of the Indian Ocean Dipole on Sea Level and Gyre Circulation of the Western Tropical Pacific Ocean. J. Clim. 2020, 33, 4207–4228. [Google Scholar] [CrossRef] [Green Version]
- Merrifield, M.; Kilonsky, B.; Nakahara, S. Interannual sea level changes in the tropical Pacific associated with ENSO. Geophys. Res. Lett. 1999, 26, 3317–3320. [Google Scholar] [CrossRef]
- Nerem, R.S.; Chambers, D.P.; Choe, C.; Mitchum, G.T. Estimating Mean Sea Level Change from the TOPEX and Jason Altimeter Missions. Mar. Geod. 2010, 33, 435–446. [Google Scholar] [CrossRef]
- Long, X.Y.; Widlansky, M.J.; Schloesser, F.; Thompson, P.R.; Annamalai, H.; Merrifield, M.A.; Yoon, H. Higher Sea Levels at Hawaii Caused by Strong El Niño and Weak Trade Winds. J. Clim. 2020, 33, 3037–3059. [Google Scholar] [CrossRef]
- Fu, L.; Qiu, B. Low-frequency variability of the North Pacific Ocean: The roles of boundary- and wind-driven baroclinic Rossby waves. J. Geophys. Res. Ocean. 2002, 107, 3220. [Google Scholar] [CrossRef]
- Zhuang, W.; Qiu, B.; Du, Y. Low-frequency western Pacific Ocean sea level and circulation changes due to the connectivity of the Philippine archipelago. J. Geophys. Res. 2013, 118, 6759–6773. [Google Scholar] [CrossRef]
- Qiu, B.; Chen, S. Interannual-to-Decadal Variability in the Bifurcation of the North Equatorial Current off the Philippines. J. Phys. Oceanogr. 2010, 40, 2525–2538. [Google Scholar] [CrossRef]
- Mantua, N.J.; Hare, S.R.; Zhang, Y.; Wallace, J.M.; Francis, R.C. A Pacific interdecadal climate oscillation with impacts on salmon production. Bull. Am. Meteorol. Soc. 1997, 78, 1069–1079. [Google Scholar] [CrossRef]
- Wu, B.Y.; Wang, J. Winter Arctic oscillation, Siberian high and East Asian winter monsoon. Geophys. Res. Lett. 2002, 29, 1897. [Google Scholar] [CrossRef]
- Feng, W.; Zhong, M.; Xu, H.Z. Sea level variation in the South China Sea inferred from satellite gravity, altimetry, and oceanographic data. Sci. China Earth Sci. 2012, 55, 1696–1701. [Google Scholar] [CrossRef]
- Peng, D.J.; Palanisamy, H.; Cazenave, A.; Meyssignac, B. Interannual Sea Level Variations in the South China Sea Over 1950–2009. Mar. Geod. 2013, 36, 164–182. [Google Scholar] [CrossRef]
- Wu, L.L.; Wang, X.L.L.; Yang, F. Historical wave height trends in the South and East China Seas, 1911-2010. J. Geophys. Res. Ocean. 2014, 119, 4399–4409. [Google Scholar] [CrossRef]
- Zhou, J.; Li, P.L.; Yu, H.L. Characteristics and mechanisms of sea surface height in the South China Sea. Glob. Planet. Chang. 2012, 88, 20–31. [Google Scholar] [CrossRef]
- Deng, W.F.; Wei, G.J.; Xie, L.H.; Ke, T.; Wang, Z.B.; Zeng, T.; Liu, Y. Variations in the Pacific Decadal Oscillation since 1853 in a coral record from the northern South China Sea. J. Geophys. Res. Ocean. 2013, 118, 2358–2366. [Google Scholar] [CrossRef] [Green Version]
- Han, S.L. Estimation of extreme sea levels along the Bangladesh coast due to storm surge and sea level rise using EEMD and EVA. J. Geophys. Res. Ocean. 2013, 118, 4273–4285. [Google Scholar] [CrossRef]
- Church, J.A.; White, N.J.; Hunter, J.R. Sea-level rise at tropical Pacific and Indian Ocean islands. Glob. Planet. Chang. 2006, 53, 155–168. [Google Scholar] [CrossRef]
- Nidheesh, A.G.; Lengaigne, M.; Vialard, J.; Izumo, T.; Unnikrishnan, A.S.; Meyssignac, B.; Hamlington, B.; Boyer Montegut, C. Robustness of observation-based decadal sea level variability in the Indo-Pacific Ocean. Geophys. Res. Lett. 2017, 44, 7391–7400. [Google Scholar] [CrossRef] [Green Version]
- Moon, J.; Song, Y.T.; Lee, H.K. PDO and ENSO modulations intensified decadal sea level variability in the tropical Pacific. J. Geophys. Res. Ocean. 2015, 120, 8229–8237. [Google Scholar] [CrossRef]
- Deepa, J.S.; Gnanaseelan, C.; Mohapatra, S.; Chowdary, J.S.; Karmakar, A.; Kakatkar, R.; Parekh, A. The Tropical Indian Ocean decadal sea level response to the Pacific Decadal Oscillation forcing. Clim. Dyn. 2019, 52, 5045–5058. [Google Scholar] [CrossRef]
- Deepa, J.S.; Gnanaseelan, C.; Parekh, A. The sea level variability and its projections over the Indo-Pacific Ocean in CMIP5 models. Clim. Dyn. 2021, 57, 173–193. [Google Scholar] [CrossRef]
- Piecuch, C.G.; Thompson, P.R.; Ponte, R.M.; Merrifield, M.A.; Hamlington, B.D. What Caused Recent Shifts in Tropical Pacific Decadal Sea-Level Trends? J. Geophys. Res. Ocean. 2019, 124, 7575–7590. [Google Scholar] [CrossRef]
- Hu, Z.Z.; Kumar, A.; Ren, H.L.; Wang, H.; L’Heureux, M.; Jin, F.F. Weakened Interannual Variability in the Tropical Pacific Ocean since 2000. J. Clim. 2013, 26, 2601–2613. [Google Scholar] [CrossRef]
- Thomson, R.E.; Tabata, S. Steric height trends at Ocean Station PAPA in the northeast Pacific Ocean. Mar. Geod. 1987, 11, 103–113. [Google Scholar] [CrossRef]
- Gharineiat, Z.; Deng, X.L. Description and assessment of regional sea-level trends and variability from altimetry and tide gauges at the northern Australian coast. Adv. Space Res. 2018, 61, S0273117718301984. [Google Scholar] [CrossRef] [Green Version]
- Nidheesh, A.G.; Lengaigne, M.; Vialard, J.; Unnikrishnan, A.S.; Dayan, H. Decadal and long-term sea level variability in the tropical Indo-Pacific Ocean. Clim. Dyn. 2013, 41, 381–402. [Google Scholar] [CrossRef]
- Wyrtki, K. Investigation of the EI Nino Phenomenon in the Pacific Ocean. Environ. Conserv. 1975, 2, 281. [Google Scholar] [CrossRef]
- Li, S.; Zhao, J.; Li, Y.; Qu, P. Study on Decadal Variability of Sea Surface Height in the Tropical Pacific Ocean. Adv. Mar. Sci. 2008. [Google Scholar] [CrossRef]
- Zhu, Z.N.; Zhu, X.H.; Guo, X.Y. Coastal tomographic mapping of nonlinear tidal currents and residual currents. Cont. Shelf Res. 2017, 143, 219–227. [Google Scholar] [CrossRef]
- Palanisamy, H.; Cazenave, A.; Delcroix, T.; Meyssignac, B. Spatial trend patterns in the Pacific Ocean sea level during the altimetry era: The contribution of thermocline depth change and internal climate variability. Ocean. Dyn. 2015, 65, 341–356. [Google Scholar] [CrossRef]
- Matthew, J.W.; Axel, T.; Karl, S.; Shayne, M.; Niklas, S.; Matthew, H.E.; Matthieu, L.; Wenju, C. Changes in South Pacific rainfall bands in a warming climate. Nat. Clim. Chang. 2013, 3, 417–423. [Google Scholar] [CrossRef] [Green Version]
- Matthew, J.; Widlansky, A.T.; Wenju, C. Future extreme sea level seesaws in the tropical Pacific. Sci. Adv. 2015, 1, e1500560. [Google Scholar] [CrossRef] [Green Version]
- Gaël, A.; Thierry, D. Interannual sea level changes and associated mass transports in the tropical Pacific from TOPEX/Poseidon data and linear model results (1964–1999). J. Geophys. Res. Ocean. 2002, 107, 17-1–17-22. [Google Scholar] [CrossRef]
- Nerem, R.S.; Chambers, D.P.; Leuliette, E.W.; Mitchum, G.T.; Giese, B.S. Variations in global mean sea level associated with the 1997–1998 ENSO event: Implications for measuring long-term sea level change. Geophys. Res. Lett. 1999, 26, 3005–3008. [Google Scholar] [CrossRef]












| Model Experiments | Descriptions |
|---|---|
| Exp 0 | Control experiment, model domain (30°S–65°N, 100°E–70°W, NPO) closed lateral boundaries, originally forced by monthly ERA-5 wind stress. |
| Exp 1 | The model domain as Exp 0. Originally forced by monthly wind stress over the north Pacific (north of 20°N, NNP); monthly climatological wind over other regions |
| Exp 2 | The model domain as Exp 0. Originally forced by monthly wind stress over the tropical Pacific Ocean (20°S–20°N, 100°E–70°W, TPO); monthly climatological wind over other regions |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Li, J.; Yin, J.; Tan, W.; Liu, Y. Sea Level Seasonal, Interannual and Decadal Variability in the Tropical Pacific Ocean. Remote Sens. 2021, 13, 3809. https://doi.org/10.3390/rs13193809
Wang J, Li J, Yin J, Tan W, Liu Y. Sea Level Seasonal, Interannual and Decadal Variability in the Tropical Pacific Ocean. Remote Sensing. 2021; 13(19):3809. https://doi.org/10.3390/rs13193809
Chicago/Turabian StyleWang, Jianhu, Juan Li, Jiyuan Yin, Wei Tan, and Yuchen Liu. 2021. "Sea Level Seasonal, Interannual and Decadal Variability in the Tropical Pacific Ocean" Remote Sensing 13, no. 19: 3809. https://doi.org/10.3390/rs13193809
APA StyleWang, J., Li, J., Yin, J., Tan, W., & Liu, Y. (2021). Sea Level Seasonal, Interannual and Decadal Variability in the Tropical Pacific Ocean. Remote Sensing, 13(19), 3809. https://doi.org/10.3390/rs13193809